En general, los medios tienen un efecto rezagado en el KPI, y ese efecto disminuye con el tiempo. Para modelar el efecto rezagado, transformamos la ejecución de los medios de un canal determinado a través de la función de Adstock:
donde:
\(w(s; \alpha) \) es una función de ponderación no negativa.
\(x_s \geq 0\) es la ejecución de los medios en el momento \(s\).
\(\alpha\ \in\ [0, 1]\) es el parámetro de decaimiento.
\(L\) es la duración máxima del rezago.
Meridian proporciona dos curvas de decaimiento: geométrica y binomial. La velocidad a la que disminuye el efecto de los medios se rige por la elección de la función junto con el parámetro alfa obtenido. El parámetro adstock_decay_spec de ModelSpec define qué función o combinación de funciones se utiliza.
Por ejemplo, si deseas usar el decaimiento binomial para todos los canales, puedes aplicar lo siguiente:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec='binomial'
)
En cambio, si quieres usar un decaimiento binomial, uno geométrico y otro binomial para tres canales denominados
"Channel0", "Channel1" y "Channel2", respectivamente, puedes especificar lo siguiente:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec=dict(
Channel0='binomial',
Channel1='geometric',
Channel2='binomial',
)
)
En general, recomendamos usar el decaimiento binomial cuando creas que una proporción significativa de los efectos rezagados de un canal de medios persiste en la segunda mitad de la ventana de efectos. En los demás casos, recomendamos usar el decaimiento geométrico.
Estas funciones definen pesos \(w(s; \alpha)\) para la función de Adstock. Se definen de manera tal que, en el momento \(t\), la ejecución de los medios en el momento \(t-s\) tenga el peso \(w(s; \alpha) / \sum_{s\in{\{0, ..., L\}}}w(s; \alpha)\). Para obtener más detalles sobre la función de Adstock, consulta Saturación y rezago de los medios.
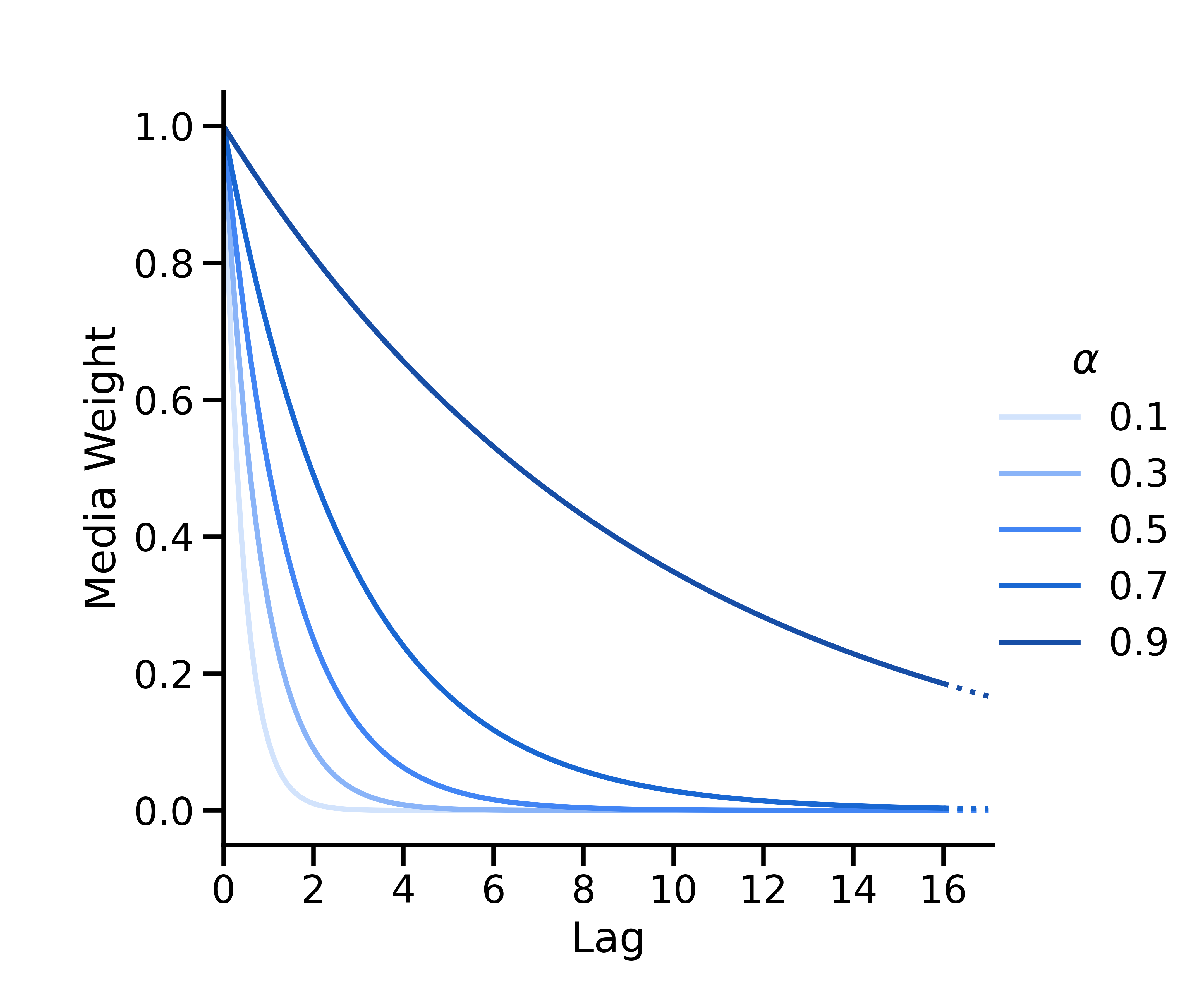
Decaimiento geométrico
El decaimiento geométrico se parametriza como \(w(s; \alpha) = \alpha^s\), donde \(\alpha \in [0, 1] \) es el parámetro geométrico que denota la tasa de decaimiento y \(s\) es el rezago. En el momento \(t\), la ejecución de los medios en el momento \(t-s\) tiene un peso \(w(s; \alpha) = \alpha^s\), que luego se normaliza para que todos los pesos sumen un valor de uno.
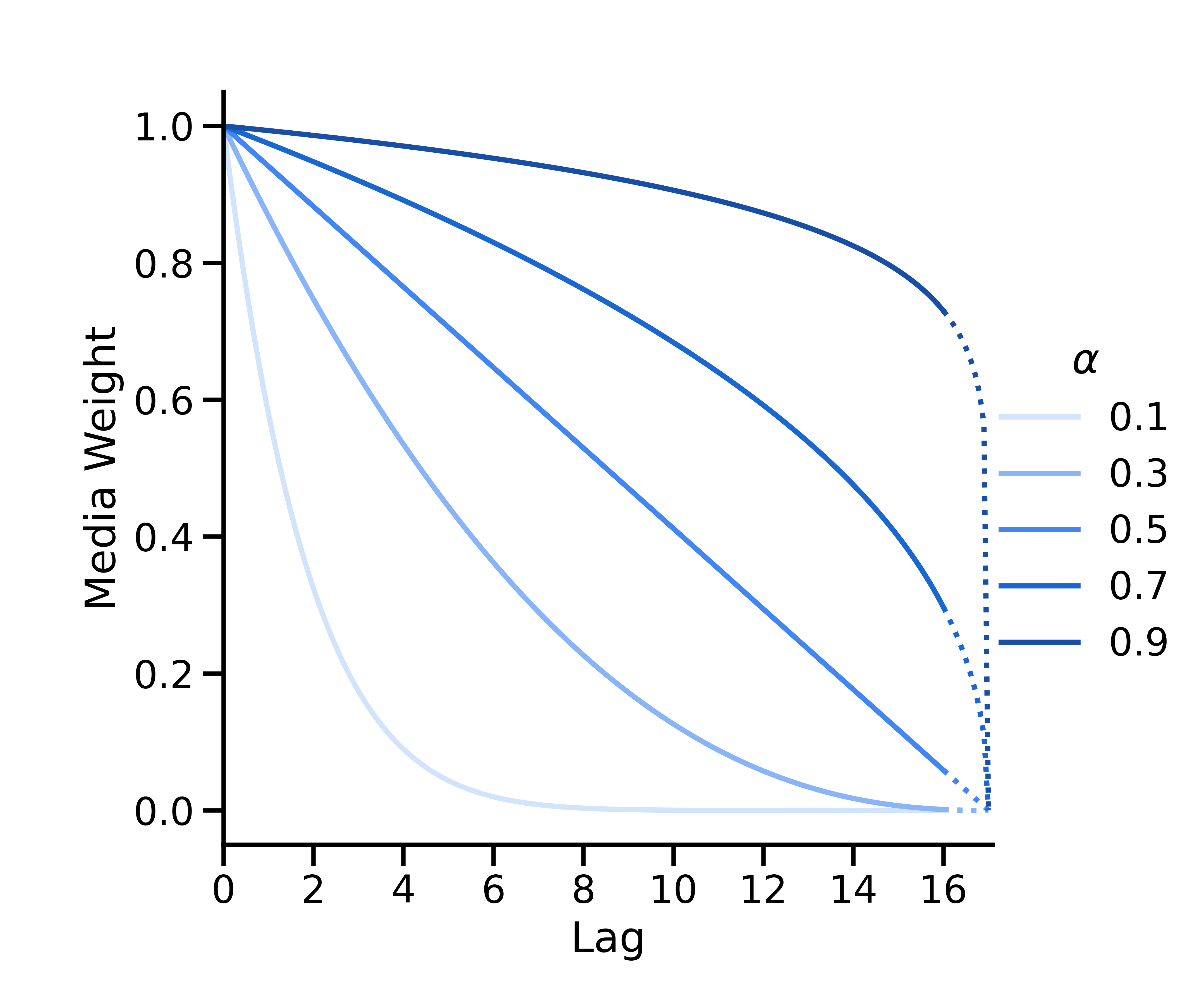
Decaimiento binomial
La decaimiento binomial se parametriza de la siguiente manera:
donde \(L\) es el rezago máximo (el parámetro max_lag de ModelSpec). La asignación \(\alpha_*=\frac{1}{\alpha} - 1\) se usa para asociar valores de
\(\alpha\) de \([0, 1]\) a \([0, \infty)\).
La curva binomial es convexa si \(\alpha < 0.5\), lineal si \(\alpha = 0.5\) y cóncava si \(\alpha > 0.5\). Se define de tal manera que su intersección con el eje X se dé siempre en \(L + 1\).
Elige entre el decaimiento geométrico y el binomial
Te recomendamos que selecciones el decaimiento binomial cuando creas que un canal tiene una proporción significativa de los efectos en la segunda mitad de la ventana de efectos. En los demás casos, elige el decaimiento geométrico.
La curva de decaimiento afecta los pesos relativos de los medios rezagados. Aumentar el peso relativo de los períodos posteriores necesariamente disminuye el peso relativo de los períodos anteriores. La curva de decaimiento binomial define los pesos que decaen al valor de cero de forma más gradual que la curva geométrica. Por lo tanto, la curva de decaimiento binomial fomenta que una mayor proporción del efecto total de los medios de un canal se produzca en los períodos posteriores; en cambio, la de decaimiento geométrico hace que esa mayor proporción se produzca en los períodos anteriores. Como la curva de decaimiento binomial se "estira" para abarcar la ventana de efectos, es una buena opción cuando se usan valores más grandes de
max_lag, ya que su intersección con el eje X se da siempre en \(L + 1\). Consulta Cómo establecer el parámetro max_lag para obtener más detalles.
Puede ser tentador seleccionar la curva de decaimiento binomial para todos los canales debido a su capacidad para admitir valores de max_lag más grandes. Sin embargo, ten en cuenta que no todos los canales se modelarán mejor con esa curva, que es más adecuada cuando crees que un canal tiene una proporción significativa de los efectos en la segunda mitad de la ventana de efectos. La aplicación incorrecta de la curva de decaimiento binomial puede generar una subestimación de efectos a corto plazo.
| Función | Geométrica | Binomial |
|---|---|---|
| Uso ideal | Medios con efectos de corta duración. | Medios con efectos que persisten hasta la segunda mitad de la ventana de efectos. |
| Forma de la curva | Decaimiento rápido. | Puede persistir más tiempo antes de decaer. |
| Recomendación de rezago máximo | 2 a 10 períodos. | 4 a 20 períodos. |
| Desventajas | Es vulnerable a una subestimación de efectos a largo plazo. | Es vulnerable a una subestimación de efectos a corto plazo. |
Consideraciones sobre los efectos a largo plazo
Si prevés efectos a largo plazo que no se están materializando en un modelo, puede ser útil utilizar alguna combinación de la curva de decaimiento binomial que modifique la distribución a priori en alfa y cambie el parámetro max_lag. Usa las curvas de probabilidad a priori de
MediaEffects.plot_adstock_decay
para ver cómo interactúan entre sí el parámetro max_lag, la distribución a priori alfa y la función de decaimiento. Luego, puedes ajustarlos para alinear un modelo con tus suposiciones iniciales sobre los efectos rezagados. Puedes modificar la distribución a priori y el parámetro max_lag a la vez que seleccionas o excluyes una función de decaimiento en particular. Te recomendamos que experimentes con diferentes combinaciones para equilibrar la convergencia, el ajuste del modelo y la ventana de efectos. Consulta
Cómo establecer el parámetro max_lag
para obtener más detalles sobre cómo seleccionar un valor de max_lag.
La distribución a priori alfa
La distribución a priori alfa predeterminada en Meridian es \(U(0, 1)\), que es una distribución a priori no informativa para las funciones de decaimiento geométricas y binomiales. Si tienes alguna intuición sobre la velocidad a la que disminuye el efecto de los medios en un canal en particular, puedes establecer una distribución a priori alfa personalizada en ese canal para informar a Meridian sobre esa intuición.
Tanto para el decaimiento geométrico como para el binomial, existe una relación monotónica entre \(\alpha\) y la velocidad a la que disminuye el efecto de los medios: un valor de \(\alpha\) más pequeño corresponde a un decaimiento más rápido y un valor de \(\alpha\) más grande corresponde a un decaimiento más corto. Las funciones geométrica y binomial maximizan los efectos a corto plazo cuando \(\alpha=0\), en cuyo caso no hay efectos rezagados, y maximizan los efectos a largo plazo cuando \(\alpha=1\), en cuyo caso todos los medios dentro de la ventana de rezago histórico se ponderan equitativamente.
En consecuencia, recomendamos establecer una distribución a priori en alfa con una mayor parte de su masa cerca de cero para fomentar un decaimiento más rápido y efectos a corto plazo. Por ejemplo, una distribución beta(1, 3) tiene más masa cerca de cero en comparación con la distribución uniforme predeterminada. Por el contrario, recomendamos establecer una distribución a priori con una mayor parte de su masa cerca de uno para fomentar un decaimiento más lento y efectos a largo plazo. Por ejemplo, una distribución beta(3, 1) tiene más masa cerca de uno en comparación con la distribución uniforme predeterminada. Para confirmar que las distribuciones a priori personalizadas coincidan con tus intuiciones, te recomendamos trazar las distribuciones a priori de los pesos de alfa y de los medios (con MediaEffects.plot_adstock_decay).
La asignación binomial \(\alpha\)
La asignación \(\alpha_*: [0, 1]\rightarrow[0, \infty) \) se realiza porque la función binomial decae para \(\alpha_* \in [0, \infty)\) , mientras que la función geométrica decae para \(\alpha \in [0, 1]\). Esta asignación permite que las distribuciones a priori definidas en el intervalo \([0, 1]\) se traduzcan correctamente a \([0, \infty)\) en el caso binomial. Además, conserva la coherencia de la especificación del modelo con el decaimiento geométrico, con valores bajos de alfa que implican un decaimiento rápido y efectos a corto plazo, y valores más altos de alfa que implican un decaimiento lento y efectos a largo plazo.
Opción avanzada: Establece una distribución a priori personalizada directamente en \(\alpha_*\) si usas el decaimiento binomial
Meridian usa una distribución a priori predeterminada de \(U(0, 1)\) en \(\alpha\) para las funciones geométricas y binomiales. Con el decaimiento binomial, una distribución a priori de \(U(0, 1)\) en \(\alpha\) es equivalente a una distribución a priori de Lomax(1, 1) en \(\alpha_*\):

Esta sigue siendo una distribución a priori relativamente no informativa para permitir que, con el decaimiento binomial, los datos fundamenten la tasa de decaimiento.
Meridian espera que las distribuciones a priori \(\alpha\) personalizadas admitan \([0, 1]\) (por ejemplo, una distribución beta) que luego se asignará a los números reales no negativos con \(1/x-1\). Sin embargo, si deseas poder definir una distribución a priori en \(\alpha_*\) que admita \([0, \infty)\) , puedes definirla y luego transformarla con la asignación inversa \(\frac{1}{1+x}\). Esta asignación está disponible a través del método de ayuda
adstock_hill.transform_non_negative_reals_distribution.
Por ejemplo, para obtener una distribución a priori normal logarítmica en \(\alpha_*\) con una media de 0.5 y una varianza de 0.5, haz lo siguiente:
import tensorflow as tf
# Example: pick mu, sigma so that the mean, variance of alpha_* are both 0.5
mu = -tf.math.log(2.0) - 0.5 * tf.math.log(3.0)
sigma = tf.math.sqrt(tf.math.log(3.0))
alpha_star_prior = tfp.distributions.LogNormal(mu, sigma) # prior on alpha_* for binomial
alpha_prior = adstock_hill.transform_non_negative_reals_distribution(alpha_star_prior)
prior = prior_distribution.PriorDistribution(
alpha_m=alpha_prior
)
model_spec = spec.ModelSpec(
prior=prior,
adstock_decay_spec='binomial'
)
Luego, también puedes interrogar la distribución a priori alfa directamente. Por ejemplo, para ver la función de densidad de probabilidad en alfa, haz lo siguiente:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, alpha_prior.prob(x), linewidth=3)
ax.set(xlabel='Alpha', ylabel='Probability')
plt.show()

Este gráfico muestra la distribución a priori en \(\alpha\) que genera una distribución a priori normal logarítmica on \(\alpha_*\) con una media y una varianza de 0.5 y 0.5, respectivamente.
