このセクションでは、メリディアンの主要指標である増分効果、費用対効果(ROI)、限界費用対効果(mROI)、応答曲線について説明します。
要点
増分効果、費用対効果(ROI)、限界費用対効果(mROI)、応答曲線を使うと、モデルの分析結果を実践的なビジネス戦略に落とし込み、「チャネルのパフォーマンスはどれくらい成果を上げたのか?」、「次はどのチャネルに投資すべきか?」といった、マーケティングに関する特に重要な質問に答えることができます。
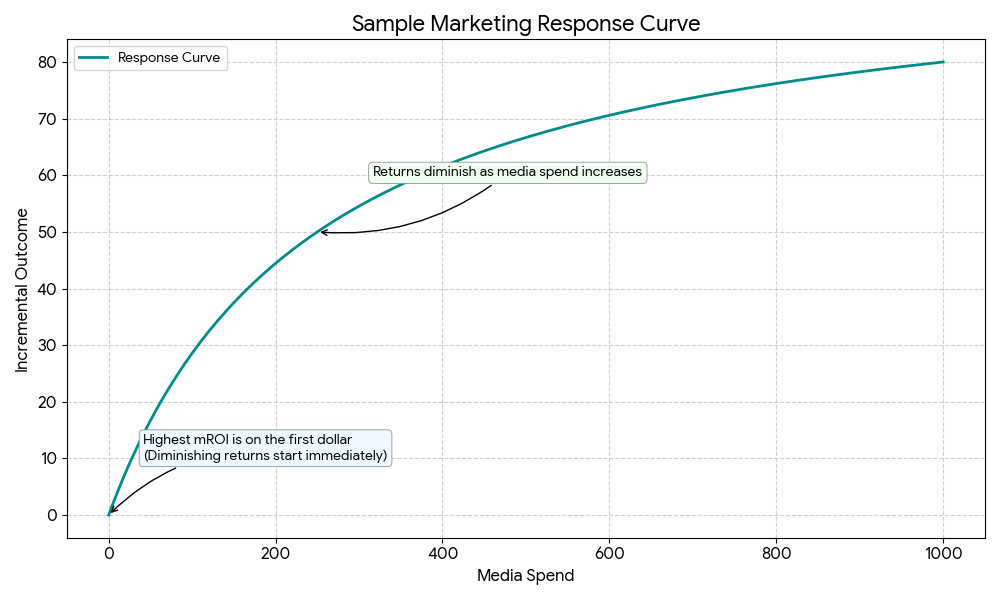
これらの指標を把握すれば、特に効率的なチャネルを特定し、現在の飽和度を把握し、ビジネスの成果を最大化するように予算を最適化できます。特に応答曲線は、費用増に伴う増分効果の変化を視覚的に表すもので、データに基づく予算配分を支える基盤となります。
マーケティングの例
オンラインの靴屋を経営しているとします。動画メディア チャネルでのマーケティングに 10,000 ドルを投じていますが、メリディアン モデルを実行したところ、その動画チャネルのおかげで売り上げが 25,000 ドル増えたことがわかりました。
- 増分効果は、マーケティングによって生み出された価値です。たとえば、総売上高が 150,000 ドルだったとしても、マーケティング キャンペーンを実施していなければ売上高が 125,000 ドルだったとメリディアンが推定した場合、その差額の 25,000 ドルが増分効果となります。
- 費用対効果は 2.50 ドル(売上高 25,000 ドル ÷ 費用 10,000 ドル)となり、投資額 1 ドルあたりの収益は 2.50 ドルとなります(この計算方法について詳しくは、ROI と応答曲線を読み解く際の考慮点をご覧ください)。
- 応答曲線は、投資額を変えた場合の売上高の変化を示しており、投資額をさらに費やしても、その効果は徐々に小さくなることがわかります。
- mROI は、投資額をわずかに(たとえば 1 ドル)増やして得られる収益です。ご利用のチャネルが飽和状態に近づくと mROI は 0.80 ドルにしかならず、他のチャネルに投資すべきタイミングであることが示唆されています。
経験則に基づく推奨事項
- ROI を使って過去のパフォーマンスを評価する: これにより、特定のチャネルに対する過去の投資の効果のほどを、明確に総合的に評価できます。
- 応答曲線を使って今後の予算を最適化する: 応答曲線によって収益逓減のポイントが可視化されるため、あるチャネルに対して投資効果が薄れる前にどの程度まで投資できるかを把握できます。
- mROI を使って飽和度を評価する: ROI に比べて mROI が大幅に低い場合、そのチャネルは過去の費用レベルで飽和し始めています。mROI が特に高いチャネルは、追加投資に最適なチャネルです。
比較表
| 指標 | 最適な用途 | 定義 |
|---|---|---|
| ROI | 過去のパフォーマンスの評価。 | チャネル全体での過去の平均値。 |
| 応答曲線 | 今後の費用の最適化、収益逓減の可視化。 | 投資額に応じた増分効果。 |
| mROI | 現在の飽和度の把握。 | 追加で 1 ドルを投じた場合の効果。 |
サンプルコード
実際のコード例については、例 - メリディアンでの ROI、mROI、応答曲線をご覧ください。
詳細な説明
このセクションでは、ROI、mROI、応答曲線の定義と方法論について詳しく説明します。
増分効果の説明
ROI、mROI、応答曲線の基盤は増分効果です。これは特定のマーケティング活動で引き出された成果(売上高やコンバージョン数など)であり、メリディアンでは実際の成果と反事実的シナリオ(実施されたマーケティング活動がまったく行われなかったシナリオ)を比較して算出されます。有料メディアの場合は、増分効果と投資額を次の観点で関連付けて解釈することができます。
- 応答曲線は、あらゆる費用レベルでの増分効果を見積もります。
- ROI は、過去の費用レベルでの増分効果を、その費用で割った値です。
- mROI は、過去の予算レベルよりも費用を 1 ドル増やした場合の増分効果です。
応答曲線の生成方法
応答曲線とは、ある 1 つのチャネルについて費用と増分効果の関係を視覚化するものです(他のすべてのチャネルの費用は現在と同額だという前提です)。
メリディアンは、ある 1 つのチャネルについて、さまざまな費用レベルでこの曲線を生成します。チャネルの過去の費用を係数で増減し(過去の費用の 1.2 倍など)、それぞれの費用レベルでの増分効果を推定します。この係数調整の際は、過去の費用配分の期間と地域(フライティング パターン)が保持されます。この処理により、チャネルが飽和状態になって追加投資の効果が薄まり始めるポイントが明らかになります。
ROI と応答曲線を読み解く際の留意点
- 遅延効果: ROI は、ある期間のチャネルの総費用を分母として、同じ期間に発生した増分効果を分子として定義されます。この分子には、その期間前に掲載された広告の遅延効果が含まれますが、その期間中に掲載された広告が将来的にもたらす効果は含まれません。1 年などの長い期間でみると、遅延効果が ROI の推定値に及ぼす影響は軽微ですが、期間が短い場合は、遅延効果の影響が大きくなる可能性があります。
- 外挿リスク: メリディアン モデルは、増分効果を計算するために、費用がゼロだったらどうなっていたかを推定する必要があります。常に一定の費用がチャネルに投じられている場合は、この費用ゼロのシナリオに関するデータがほとんどないため、モデルは学習した前提に基づいて外挿(既存データの範囲外を推定)する必要があります。外挿リスクは、応答曲線の過去の費用を超えるポイントでの増分効果の推定にも影響し、過去の費用を大幅に超えるほどリスクが高まります。
数学的付録
このセクションでは、結果の増分、費用対効果、限界費用対効果、応答曲線などの主なエスティマンドが、メリディアンでどのように定義されているのかを説明します。これらの量は、因果推論の言語である潜在結果と反事実的条件法を使用して定義されます。
エスティマンドを明確に定義することで、MMM が有効な推論を導き出すために必要な仮説を確認できます。こうした仮説は、モデルが実際にこれらの量を推定できるようにするのに役立ちます。仮説が満たされていない場合、エスティマンドに大きな偏りが生じる可能性があります。
MMM の手法に必要な因果エスティマンドと仮説を明確に定義することをおすすめします。これを行わないと、モデルの結果が誤って解釈される可能性があります。さらに影響が大きいのは、必要な仮説を無視すると、根本的なバイアスが非常に大きくなるため、分析が実質的に無意味になる可能性があるということです。
以下のセクションの定義は、メリディアン モデル仕様のどの側面にも左右されません。同じ定義がどの MMM にも当てはまります。MMM 分析では、結果を解釈可能な状態にして、特定のモデルが分析に適しているか、どのような仮説が適しているかを判断するためには、因果エスティマンドを定義することが重要です。
増分効果
まずは、ROI、mROI、応答曲線の基盤となる増分効果の定義から説明します。
増分効果を導き出す因果推論フレームワーク
メリディアンは、介入変数が結果に及ぼす因果効果を測定します。通常「結果」は収益ですが、KPI が収益でなく revenue_per_kpi データが使えない場合は、その KPI そのものが結果であると定義されます。
「増分効果」は、因果推論のフレームワークを使って定義されます。因果推論では、「介入群」と「コントロール群」の反事実的シナリオでの潜在的結果を、 \(Y^{(1)}\) や\(Y^{(0)}\) などの表記を使って表すことが一般的です。メリディアンの場合も同様ですが、もう少し複雑で、介入群とコントロール群の反事実的シナリオが 3 次元配列(地域 $g$、時間 $t$、介入変数 $i$)になります。介入群とコントロール群の反事実的シナリオは、それぞれ\(\left\{x^{(1)}_{g,t,i}\right\}\) 、 \(\left\{x^{(0)}_{g,t,i}\right\}\)と表記されます。また、この潜在的結果は地域と時間の 2 次元配列になります。介入群とコントロール群の反事実的シナリオでの潜在的結果は、それぞれ\(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(1)} \right\}\right)}\)、 \(\overset\sim Y_{g,t}^{\left(\left\{ x_{g,t,i}^{(0)} \right\}\right)}\)と表記されます。
反事実的シナリオを選ぶ際には、次の要素が判断に役立ちます。
反事実的シナリオでは、コンバージョン数を観測できません。両方のシナリオの潜在的結果を観測することはできないからです。観測できるのは、せいぜい 1 つの反事実的シナリオです。そこで代わりに、 \(\{x^{(1)}_{g,t,i} \}\) と\(\{ x^{(0)}_{g,t,i} \}\)の 2 つの反事実的介入群シナリオで、増分効果を次のように定義します。
ここで \(\{z_{g,t,i}\}\) は、一連のコントロール変数の観測値を表します。この簡略表記は、コントロール確率変数がこれらの値を取ることを前提とした、条件付きの期待値であることを示すために使われます。この条件付き期待値は、MMM 回帰モデルと、慎重に選ばれた一連のコントロール変数を使うことで、推定可能になります。詳しくは、回帰を使った増分効果の推定をご覧ください。
通常、合計は \(g=1,\dots G\) と \(t=1,\dots T\)の値を対象に計算されますが、これらの値の任意の組み合わせでも増分効果を定義できます。
メリディアンで使われる反事実的シナリオ
incremental_outcome は、反事実的シナリオを検討するうえで十分な柔軟性を備えていますが、メリディアンがデフォルトで使用するのは、特定のペアの反事実的介入群シナリオです。ROI、mROI、応答曲線は incremental_outcome のデフォルト設定に基づいているため、この特定のペアが重要になります。
メリディアンは \(\left\{x^{(1)}_{g,t,i}\right\}\) を過去の実際の値とし、 \(\left\{x^{(0)}_{g,t,i}\right\}\) についても過去の実際の値としますが、特定の 1 つの介入群変数のすべての値に関してはベースライン値に設定します。有料メディアとオーガニック メディアの場合、ベースライン値は 0 です。メディア以外の介入変数の場合、ベースライン値は、観測された変数の最小値(デフォルト)、最大値、またはユーザー指定の浮動小数点数に設定できます。
特定の介入群変数 \(q\)について、増分効果は次のように定義されます。
\[\text{IncrementalOutcome}_q = \text{IncrementalOutcome} \left(\Bigl\{ x_{g,t,i} \Bigr\}, \Bigl\{ x_{g,t,i}^{(0,q)} \Bigr\} \right)\]
ここで:
- \(\left\{ x_{g,t,i}\right\}\) は、観測された介入群の値です。
- \(\left\{ x_{g,t,i}^{(0,q)} \right\}\) は、介入群 \(q\)を除くすべての介入群で観測された介入群値を表し、常にベースライン値 \(b_q\) に設定されます。具体的には次のようになります。
- \(x_{g,t,q}^{(0,q)}=b_q\ \forall\ g,t\)
- \(x_{g,t,i}^{(0,q)}=x_{g,t,i}\ \forall\ g,t,i \neq q\)
なお、反事実的メディア シナリオ(\(\left\{ x_{g,t,i}^{(0,q)} \right\}\))は、実際にはデータに反映されない可能性があります。その場合、反事実を推定するには、モデルの想定に基づく外挿が必要になります。
ROI
有料メディア チャネル \(q\) の ROI は次のように定義されます。
\[\text{ROI}_q = \dfrac{\text{IncrementalOutcome}_q}{\text{Cost}_q}\]
ここで \(\text{Cost}_q\) は、有料メディア チャネル \(q\) の費用を、すべての地域と時間で合計したものです。
なお ROI は、ある特定の期間におけるチャネルの総費用を分母として、同じ期間に発生した増分効果を分子として定義されます。この分子には、その期間前に掲載された広告の遅延効果が含まれますが、その期間中に掲載された広告が将来的にもたらす効果は含まれません。1 年などの長い期間でみると、遅延効果が ROI の推定値に及ぼす影響は軽微ですが、期間が短い場合は、遅延効果の影響が大きくなる可能性があります。
応答曲線
増分効果の定義を一般化すると、有料メディア チャネル \(q\) の応答曲線は、チャネル \(q\)の費用の関数として増分効果を返す関数として定義されます。
\[\text{IncrementalOutcome}_q (\omega \cdot \text{Cost}_q) = \text{IncrementalOutcome} \left(\left\{ x^{(\omega,q)}_{g,t,i} \right\}, \left\{ x^{(0,q)}_{g,t,i} \right\}\right)\]
ここで \(\left\{ x^{(\omega,q)}_{g,t,i} \right\}\) は、チャネル \(q\)を除くすべてのチャネルで観測されたメディア値を表し、常に係数 \(\omega\) で乗算されます。具体的には次のようになります。
- \(x^{(\omega,q)}_{g,t,q}=\omega \cdot x_{g,t,q}\ \forall\ g,t\)
- \(x^{(\omega,q)}_{g,t,i}=x_{g,t,i} \forall\ g,t,i \neq q\)
限界費用対効果(mROI)
有料メディア チャネル \(q\) の限界費用対効果(mROI)は次のように定義されます。
ここで \(\delta\) は、ごくわずかな量です( \(0.01\)など)。
なお、応答曲線と限界費用対効果の定義では、メディア単位あたりの費用は、過去のメディア単位あたりの費用の平均値と同じになると暗黙的に仮定されています。
