הודעה: כל הפרויקטים הלא מסחריים שנרשמו לשימוש ב-Earth Engine לפני 15 באפריל 2025 חייבים לעבור אימות של הזכאות לשימוש לא מסחרי כדי לשמור על הגישה ל-Earth Engine.

דף זה תורגם על ידי Cloud Translation API.

בניית מודלים של התפלגות מינים

Author(s): osgeokr

הפעלה ב-Google Colab

הצגת המקור ב-GitHub

במדריך הזה נציג את המתודולוגיה של מידול תפוצת מינים באמצעות Google Earth Engine. בהתחלה ניתן סקירה קצרה על מודלים של תפוצת מינים, ואחר כך נסביר על תהליך החיזוי והניתוח של בית הגידול של מין ציפורים בסכנת הכחדה שנקראת פיתה (שם מדעי: Pitta nympha).

תפעיל אותי קודם

מריצים את התא הבא כדי לאתחל את ה-API. הפלט יכלול הוראות למתן גישה למחברת הזו ל-Earth Engine באמצעות החשבון שלכם.

import ee

# Trigger the authentication flow.
ee.Authenticate()

# Initialize the library.
ee.Initialize(project='my-project')

סקירה כללית קצרה של מידול של תפוצת מינים

במאמר הזה נסביר מהם מודלים של תפוצת מינים, מהם היתרונות של שימוש ב-Google Earth Engine לעיבוד שלהם, מהם הנתונים שנדרשים למודלים ואיך בנוי תהליך העבודה.

מהו מידול של תפוצת מינים?

מודלים של תפוצת מינים (SDM בהמשך) הם המתודולוגיה הנפוצה ביותר להערכת התפוצה הגיאוגרפית בפועל או הפוטנציאלית של מין מסוים. התהליך כולל אפיון של התנאים הסביבתיים שמתאימים למין מסוים, ואז זיהוי של המקומות שבהם התנאים האלה קיימים מבחינה גיאוגרפית.

בשנים האחרונות, מידול של תפוצת מינים (SDM) הפך לרכיב חיוני בתכנון שימור, ופותחו למטרה הזו טכניקות מידול שונות. הטמעה של SDM ב-Google Earth Engine (GEE בהמשך) מספקת גישה נוחה לנתונים סביבתיים בהיקפים גדולים, יחד עם יכולות מחשוב מתקדמות ותמיכה באלגוריתמים של למידה חישובית, שמאפשרים ליצור מודלים במהירות.

הערה: הביולוג של שמירת הטבע ד"ר רמירו ד. קריגו הטמיע את SDM באמצעות עורך הקוד של GEE JavaScript ופרסם את ממצאי המחקר שלו (Crego et al, 2022). המתודולוגיה של SDM שהוצגה כאן תורגמה ושונתה מקוד המקור של JavaScript שהוא שיתף לשפת Python.

הנתונים שנדרשים ל-SDM

בדרך כלל, SDM משתמשת בקשר בין רשומות ידועות של מינים לבין משתנים סביבתיים כדי לזהות את התנאים שבהם אוכלוסייה יכולה להתקיים. במילים אחרות, נדרשים שני סוגים של נתוני קלט למודל:

רשומות של מינים מוכרים
משתני סביבה שונים

הנתונים האלה מוזנים לאלגוריתמים כדי לזהות תנאים סביבתיים שקשורים לנוכחות של מינים.

תהליך העבודה של SDM באמצעות GEE

תהליך העבודה של SDM באמצעות GEE הוא כדלקמן:

איסוף ועיבוד מקדים של נתוני מיקום של מינים
הגדרה של אזור העניין
הוספה של משתני סביבה של GEE
יצירה של נתוני היעדרות פסאודו
התאמת המודל וחיזוי
חשיבות המשתנים והערכת הדיוק

חיזוי וניתוח של בתי גידול באמצעות GEE

הפִּיטָה הנִמפָה (Pitta nympha) תשמש כמקרה לדוגמה כדי להדגים את השימוש ב-SDM שמבוסס על GEE. המין הספציפי הזה נבחר לדוגמה אחת, אבל חוקרים יכולים להחיל את המתודולוגיה על כל מין מטרה שמעניין אותם, עם שינויים קלים בקוד המקור שסופק.

פיתה יפנית היא ציפור נדירה שנודדת בקיץ ועוברת בקוריאה הדרומית, ואזור התפוצה שלה מתרחב בגלל התחממות האקלים בחצי האי הקוריאני. הוא מסווג כמין נדיר, כחיית בר בסכנת הכחדה מסוג II, כאתר טבעי מספר 204, כמין שנכחד אזורית (RE) ברשימה האדומה הלאומית, וכמין פגיע (VU) לפי הקטגוריות של IUCN.

נראה ששימוש ב-SDM לתכנון שימור של פיטה פיהירינה הוא בעל ערך רב. עכשיו נמשיך עם חיזוי וניתוח של בתי גידול באמצעות GEE.

קודם כל, מייבאים את ספריות Python.ההצהרה import מייבאת את כל התוכן של מודול, וההצהרה from import מאפשרת לייבא אובייקטים ספציפיים ממודול.

# Import libraries
import geemap

import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random

from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor

איסוף ועיבוד מקדים של נתוני מיקום של מינים

עכשיו נאסוף נתוני התרחשות של Fairy pitta. גם אם אין לכם כרגע גישה לנתוני התרחשות של המינים שמעניינים אתכם, אתם יכולים לקבל נתונים על תצפיות של מינים ספציפיים דרך GBIF API. ‫GBIF API הוא ממשק שמאפשר גישה לנתוני התפוצה של מינים שסופקו על ידי GBIF. הממשק מאפשר למשתמשים לחפש, לסנן ולהוריד נתונים, וגם לקבל מידע שונה שקשור למינים.

בדוגמה הבאה, למשתנה species_name מוקצה השם המדעי של המין (למשל, ‫Pitta nympha ל-Fairy pitta), והמשתנה country_code מקבל את קוד המדינה (למשל, KR לקוריאה הדרומית). המשתנה base_url מאחסן את הכתובת של GBIF API. ‫params הוא מילון שמכיל פרמטרים לשימוש בבקשת ה-API:

‫scientificName: הגדרת השם המדעי של המינים לחיפוש.
‫country: מגביל את החיפוש למדינה ספציפית.
‫hasCoordinate: מוודא שמתבצע חיפוש רק של נתונים עם קואורדינטות (true).
‫basisOfRecord: בחירה רק של רשומות של תצפיות אנושיות (HUMAN_OBSERVATION).
‫limit: מגדירה את המספר המקסימלי של התוצאות שיוחזרו ל-10,000.

def get_gbif_species_data(species_name, country_code):
    """
    Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.

    Parameters:
    species_name (str): The scientific name of the species to query.
    country_code (str): The country code of the where the observation data will be queried.

    Returns:
    pd.DataFrame: A pandas DataFrame containing the observational data.
    """
    base_url = "https://api.gbif.org/v1/occurrence/search"
    params = {
        "scientificName": species_name,
        "country": country_code,
        "hasCoordinate": "true",
        "basisOfRecord": "HUMAN_OBSERVATION",
        "limit": 10000,
    }

    try:
        response = requests.get(base_url, params=params)
        response.raise_for_status()  # Raises an exception for a response error.
        data = response.json()
        occurrences = data.get("results", [])

        if occurrences:  # If data is present
            df = pd.json_normalize(occurrences)
            return df
        else:
            print("No data found for the given species and country code.")
            return pd.DataFrame()  # Returns an empty DataFrame
    except requests.RequestException as e:
        print(f"Request failed: {e}")
        return pd.DataFrame()  # Returns an empty DataFrame in case of an exception

באמצעות הפרמטרים שהוגדרו קודם, אנחנו שולחים שאילתה ל-GBIF API כדי לקבל רשומות של תצפיות על פיטה פיות (Pitta nympha), וטוענים את התוצאות ל-DataFrame כדי לבדוק את השורה הראשונה. ‫DataFrame הוא מבנה נתונים לטיפול בנתונים בפורמט טבלה, שמורכב משורות ועמודות. אם צריך, אפשר לשמור את ה-DataFrame כקובץ CSV ולקרוא אותו בחזרה.

# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1)  # Display the first row of the DataFrame

לאחר מכן, ממירים את ה-DataFrame ל-GeoDataFrame שכולל עמודה למידע גיאוגרפי (geometry) ובודקים את השורה הראשונה. אפשר לשמור GeoDataFrame כקובץ GeoPackage ‏ (*.gpkg) ולקרוא אותו בחזרה.

# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
    df,
    geometry=gpd.points_from_xy(df.decimalLongitude,
                                df.decimalLatitude),
    crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1)  # Display the first row of the GeoDataFrame

הפעם יצרנו פונקציה להמחשת פיזור הנתונים לפי שנה וחודש מ-GeoDataFrame ולהצגתם כתרשים, שאפשר לשמור כקובץ תמונה. שימוש במפת חום מאפשר לנו להבין במהירות את תדירות המופעים של מינים לפי שנה וחודש, ומספק המחשה אינטואיטיבית של השינויים והדפוסים הזמניים בנתונים. כך אפשר לזהות דפוסים זמניים ושינויים עונתיים בנתוני המינים, וגם לזהות במהירות חריגות או בעיות באיכות הנתונים.

# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):

    statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)

    # Heatmap
    plt.figure(figsize=(h_size, h_size - 6))
    heatmap = plt.imshow(
        statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
    )

    # Display values above each pixel
    for i in range(len(statistics.index)):
        for j in range(len(statistics.columns)):
            plt.text(
                j, i, statistics.values[i, j], ha="center", va="center", color="black"
            )

    plt.colorbar(heatmap, label="Count")
    plt.title("Monthly Species Count by Year")
    plt.xlabel("Year")
    plt.ylabel("Month")
    plt.xticks(range(len(statistics.columns)), statistics.columns)
    plt.yticks(range(len(statistics.index)), statistics.index)
    plt.tight_layout()
    plt.savefig("heatmap_plot.png")
    plt.show()

plot_heatmap(gdf)

הנתונים משנת 1995 דלילים מאוד, עם פערים משמעותיים בהשוואה לשנים אחרות. גם בחודשים אוגוסט וספטמבר יש דגימות מוגבלות, והמאפיינים העונתיים שונים בהשוואה לתקופות אחרות. החרגת הנתונים האלה יכולה לתרום לשיפור היציבות והיכולת של המודל לבצע חיזויים.

עם זאת, חשוב לציין שהחרגת נתונים עשויה לשפר את יכולת ההכללה של המודל, אבל היא עלולה גם להוביל לאובדן של מידע חשוב שרלוונטי ליעדי המחקר. לכן, צריך לשקול היטב את ההחלטות האלה.

# Filtering data by year and month
filtered_gdf = gdf[
    (~gdf['year'].eq(1995)) &
    (~gdf['month'].between(8, 9))
]

עכשיו, ה-GeoDataFrame המסונן מומר לאובייקט של Google Earth Engine.

# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)

בשלב הבא נגדיר את גודל הפיקסל של תוצאות ה-SDM כרזולוציה של קילומטר אחד.

# Spatial resolution setting (meters)
grain_size = 1000

אם יש כמה נקודות של אירועים בתוך אותו פיקסל רסטר ברזולוציה של קילומטר אחד, סביר מאוד שהן חולקות את אותם תנאים סביבתיים באותו מיקום גיאוגרפי. שימוש ישיר בנתונים כאלה בניתוח עלול להוביל להטיה בתוצאות.

במילים אחרות, אנחנו צריכים להגביל את ההשפעה הפוטנציאלית של הטיית דגימה גיאוגרפית. כדי להשיג את זה, נשמור רק מיקום אחד בכל פיקסל של קילומטר אחד ונסיר את כל השאר, כדי שהמודל ישקף באופן אובייקטיבי יותר את התנאים הסביבתיים.

def remove_duplicates(data, grain_size):
    # Select one occurrence record per pixel at the chosen spatial resolution
    random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
    rand_point_vals = random_raster.sampleRegions(
        collection=ee.FeatureCollection(data), geometries=True
    )
    return rand_point_vals.distinct("random")


data = remove_duplicates(data_raw, grain_size)

# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())

בהמשך מוצג תרשים להשוואה בין הטיית הדגימה הגיאוגרפית לפני עיבוד מראש (בכחול) ואחרי עיבוד מראש (באדום). כדי להקל על ההשוואה, המפה ממוקמת במרכז האזור עם ריכוז גבוה של קואורדינטות של מיקום הציפור פיטה פיה בפארק הלאומי הלאסאן.

# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
    random_raster,
    {"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
    "Random Raster",
)

# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")

# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")

# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map

הגדרה של אזור העניין

המונח 'אזור עניין' (AOI) מתייחס לאזור הגיאוגרפי שהחוקרים רוצים לנתח. המשמעות שלו דומה למונח 'אזור לימודים'.

בהקשר הזה, קיבלנו את תיבת התוחמת של גיאומטריית שכבת נקודות המקרים ויצרנו סביבה מאגר נתונים זמני של 50 קילומטרים (עם סבילות מקסימלית של 1,000 מטרים) כדי להגדיר את אזור העניין.

# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)

# Add the AOI to the map
outline = ee.Image().byte().paint(
    featureCollection=aoi, color=1, width=3)

Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map

הוספה של משתני סביבה של GEE

עכשיו נוסיף משתני סביבה לניתוח. ‫GEE מספק מגוון רחב של מערכי נתונים של משתנים סביבתיים כמו טמפרטורה, משקעים, גובה, כיסוי פני השטח וטופוגרפיה. מערכי הנתונים האלה מאפשרים לנו לנתח באופן מקיף גורמים שונים שעשויים להשפיע על העדפות בית הגידול של פיטה פיות.

הבחירה של משתנים סביבתיים ב-GEE ב-SDM צריכה לשקף את מאפייני העדפת בית הגידול של המינים. לשם כך, צריך לערוך מחקר מקדים וסקירת ספרות בנושא העדפות בית הגידול של פיטה יפהפייה. המדריך הזה מתמקד בעיקר בתהליך העבודה של SDM באמצעות GEE, ולכן לא מופיעים בו פרטים מעמיקים.

‫WorldClim V1 Bioclim: מערך הנתונים הזה מספק 19 משתנים ביו-אקלימיים שנגזרים מנתוני טמפרטורה ומשקעים חודשיים. היא מכסה את התקופה מ-1960 עד 1991, והרזולוציה שלה היא 927.67 מטרים.

# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")

‫NASA SRTM Digital Elevation 30m: מערך הנתונים הזה מכיל נתוני גובה דיגיטליים מ-Shuttle Radar Topography Mission‏ (SRTM). הנתונים נאספו בעיקר בסביבות שנת 2000, והם מסופקים ברזולוציה של כ-30 מטר (שניית קשת אחת). הקוד הבא מחשב את השכבות של הגובה מעל פני הים, השיפוע, ההיבט וההצללה מנתוני ה-SRTM.

# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))

‫Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: מערך הנתונים Vegetation Continuous Fields (VCF)‎ מ-Landsat מעריך את שיעור כיסוי הצמחייה בהטלה אנכית, כשהגובה של הצמחייה גדול מ-5 מטרים. מערך הנתונים הזה מסופק לארבע תקופות זמן, סביב השנים 2000, 2005, 2010 ו-2015, ברזולוציה של 30 מטרים. במקרה הזה, המערכת משתמשת בערכי החציון מארבעת פרקי הזמן האלה.

# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
    tcc.filterDate("2000-01-01", "2015-12-31")
    .select(["tree_canopy_cover"], ["TCC"])
    .median()
)

השכבות bio (משתנים ביו-אקלימיים), terrain (טופוגרפיה) ו-median_tcc (כיסוי צל עצים) משולבות לתמונה אחת עם כמה פסים. הטווח elevation נבחר מתוך terrain, ונוצר watermask למיקומים שבהם elevation גדול מ-0. האזורים שמתחת לפני הים (למשל האוקיינוס) מוסתרים, והחוקר יכול להתכונן לניתוח מקיף של גורמים סביבתיים שונים באזור העניין.

# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)

# Create a water mask
watermask = terrain.select('elevation').gt(0)

# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)

כשמשתני חיזוי עם מתאם גבוה נכללים יחד במודל, עלולות להתעורר בעיות של מולטיקולינאריות. מולטיקולינאריות היא תופעה שמתרחשת כשיש קשרים לינאריים חזקים בין משתנים בלתי תלויים במודל, מה שמוביל לחוסר יציבות בהערכה של המקדמים (משקלים) של המודל. חוסר היציבות הזה יכול להפחית את מהימנות המודל ולהקשות על חיזויים או על פרשנויות של נתונים חדשים. לכן נבדוק את המולטיקולינאריות ונמשיך בתהליך של בחירת משתני החיזוי.

קודם ניצור 5,000 נקודות אקראיות ואז נחלץ את ערכי המשתנה לחיזוי של תמונת המולטיבנד היחידה בנקודות האלה.

# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)

# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)

נמיר את ערכי החיזוי שחולצו ל-DataFrame ואז נבדוק את השורה הראשונה.

# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)

# Displaying the columns
columns = pvals_df.columns
print(columns)

חישוב מקדמי המתאם של ספירמן בין משתני הניבוי הנתונים והצגתם בתרשים חום.

def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
    # Calculate Spearman correlation coefficients
    correlation_matrix = dataframe.corr(method="spearman")

    # Create a heatmap
    plt.figure(figsize=(h_size, h_size-2))
    plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')

    # Optionally display values on the heatmap
    if show_labels:
        for i in range(correlation_matrix.shape[0]):
            for j in range(correlation_matrix.shape[1]):
                plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
                         ha='center', va='center', color='white', fontsize=8)

    columns = dataframe.columns.tolist()
    plt.xticks(range(len(columns)), columns, rotation=90)
    plt.yticks(range(len(columns)), columns)
    plt.title("Variables Correlation Matrix")
    plt.colorbar(label="Spearman Correlation")
    plt.savefig('correlation_heatmap_plot.png')
    plt.show()

# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)

מקדם המתאם של ספירמן שימושי להבנת הקשרים הכלליים בין משתני החיזוי, אבל הוא לא מעריך ישירות את האינטראקציה בין כמה משתנים, ובמיוחד לא מזהה מולטיקולינאריות.

מקדם ניפוח השונות (VIF, בהמשך) הוא מדד סטטיסטי שמשמש להערכת מולטיקולינאריות ולבחירת משתנים. הוא מציין את מידת הקשר הליניארי של כל משתנה בלתי תלוי עם המשתנים הבלתי תלויים האחרים, וערכי VIF גבוהים יכולים להעיד על מולטיקולינאריות.

בדרך כלל, כשערכי VIF גבוהים מ-5 או מ-10, זה מצביע על כך שיש למשתנה קורלציה חזקה עם משתנים אחרים, וזה עלול לפגוע ביציבות של המודל וביכולת לפרש אותו. במדריך הזה, הקריטריון לבחירת משתנים היה ערכי VIF נמוכים מ-10. המשתנים הבאים (6) נבחרו על סמך VIF.

# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):

    original_columns = dataframe.columns.tolist()
    remaining_columns = original_columns[:]

    while True:
        vif_data = dataframe[remaining_columns]
        vif_values = [
            variance_inflation_factor(vif_data.values, i)
            for i in range(vif_data.shape[1])
        ]

        max_vif_index = vif_values.index(max(vif_values))
        max_vif = max(vif_values)

        if max_vif < threshold:
            break

        print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")

        del remaining_columns[max_vif_index]

    filtered_data = dataframe[remaining_columns]
    bands = filtered_data.columns.tolist()
    print("Bands:", bands)

    return filtered_data, bands

filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)

# Variable Selection Based on VIF
predictors = predictors.select(bands)

# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)

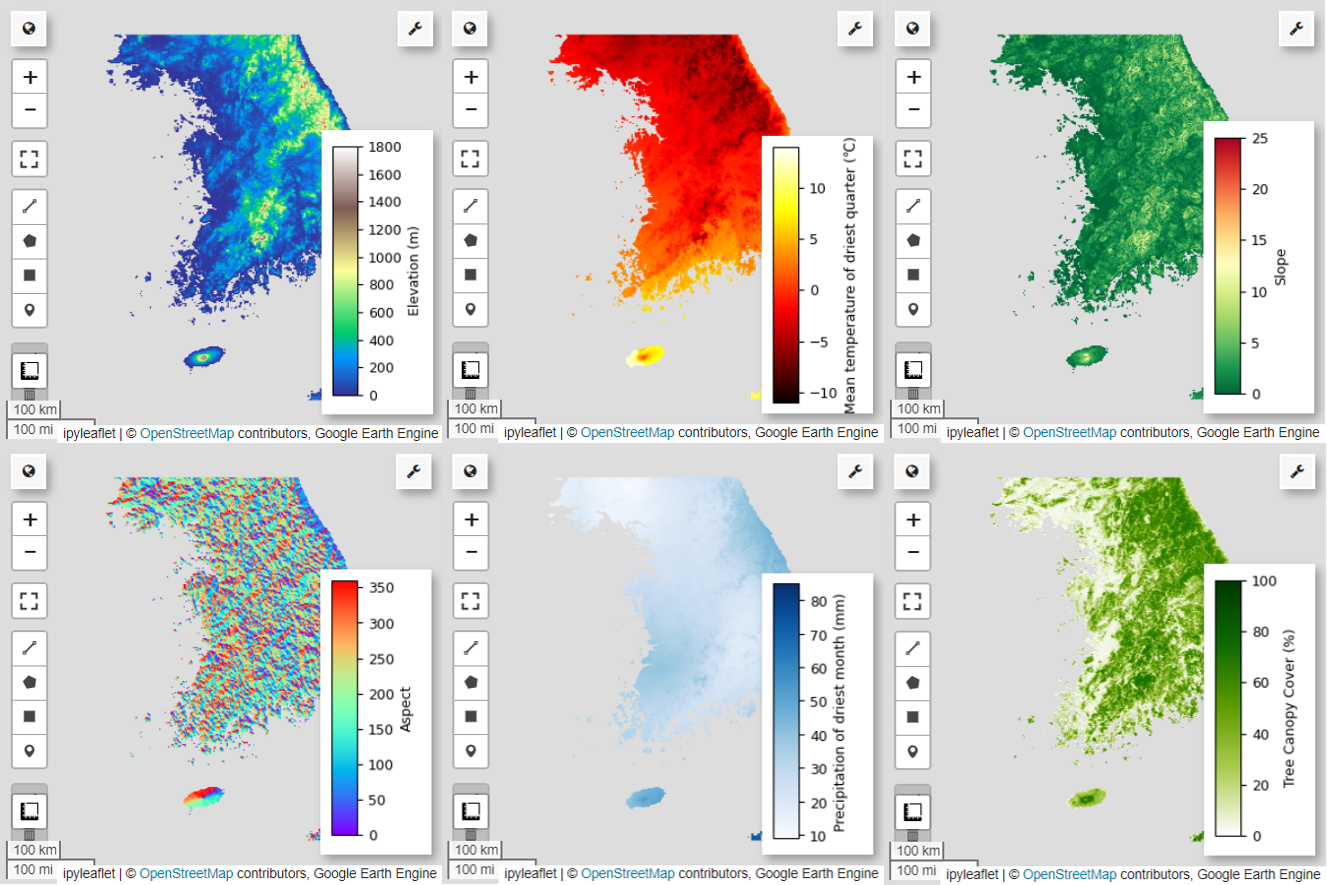
בשלב הבא, נציג באופן חזותי במפה את 6 משתני החיזוי שנבחרו. משתני חיזוי לניתוח

אפשר להשתמש בקוד הבא כדי לראות את הפלטות הזמינות לתצוגה חזותית של מפה. לדוגמה, לוח הצבעים terrain נראה כך: cm.plot_colormaps(width=8.0, height=0.2)

cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')

# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map

# Calculate the minimum and maximum values for bio09
min_max_val = (
    predictors.select("bio09")
    .multiply(0.1)
    .reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
    .getInfo()
)

# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "min": math.floor(min_max_val["bio09_min"]),
    "max": math.ceil(min_max_val["bio09_max"]),
    "palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
    vis_params,
    label="Mean temperature of driest quarter (℃)",
    orientation="vertical",
    layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map

# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map

# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map

# Calculate the minimum and maximum values for bio14
min_max_val = (
    predictors.select("bio14")
    .reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
    .getInfo()
)

# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "bands": ["bio14"],
    "min": math.floor(min_max_val["bio14_min"]),
    "max": math.ceil(min_max_val["bio14_max"]),
    "palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
    vis_params,
    label="Precipitation of driest month (mm)",
    orientation="vertical",
    layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map

# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "bands": ["TCC"],
    "min": 0,
    "max": 100,
    "palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
    vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map

יצירה של נתוני היעדרות פסאודו

בתהליך של SDM, בחירת נתוני הקלט עבור מין מסוים מתבצעת בעיקר באמצעות שתי שיטות:

שיטת הנוכחות ברקע: בשיטה הזו משווים בין המיקומים שבהם נצפה מין מסוים (נוכחות) לבין מיקומים אחרים שבהם המין לא נצפה (רקע). במקרה הזה, נתוני הרקע לא בהכרח מייצגים אזורים שבהם המינים לא קיימים, אלא הם מוגדרים כך שישקפו את התנאים הסביבתיים הכלליים של אזור המחקר. הוא משמש להבחנה בין סביבות מתאימות שבהן המינים יכולים להתקיים לבין סביבות פחות מתאימות.
שיטת נוכחות-היעדרות: בשיטה הזו משווים בין מיקומים שבהם נצפה המין (נוכחות) לבין מיקומים שבהם הוא בוודאות לא נצפה (היעדרות). במקרה הזה, נתוני היעדרות מייצגים מיקומים ספציפיים שבהם ידוע שהמין לא קיים. הנתונים לא משקפים את התנאים הסביבתיים הכוללים של אזור המחקר, אלא מצביעים על מיקומים שבהם ההערכה היא שהמין לא קיים.

בפועל, לרוב קשה לאסוף נתוני היעדרות אמיתיים, ולכן נעשה שימוש תדיר בנתוני היעדרות מדומים שנוצרו באופן מלאכותי. עם זאת, חשוב להכיר במגבלות ובטעויות הפוטנציאליות של השיטה הזו, כי נקודות פסאודו-נוכחות שנוצרו באופן מלאכותי לא תמיד משקפות בצורה מדויקת אזורים שבהם המינים לא נמצאים.

הבחירה בין שתי השיטות האלה תלויה בזמינות הנתונים, ביעדי המחקר, בדיוק ובמהימנות של המודל, וגם בזמן ובמשאבים. בדוגמה הזו נשתמש בנתוני התרחשות שנאספו מ-GBIF ובנתוני פסאודו-היעדרות שנוצרו באופן מלאכותי כדי ליצור מודל באמצעות השיטה 'נוכחות-היעדרות'.

יצירת נתוני פסאודו-היעדרות תתבצע באמצעות 'גישת פרופיל הסביבה', והשלבים הספציפיים הם:

סיווג סביבתי באמצעות קיבוץ k-means לאשכולות: אלגוריתם הקיבוץ k-means לאשכולות, שמבוסס על מרחק אוקלידי, ישמש לחלוקת הפיקסלים באזור המחקר לשני אשכולות. אשכול אחד ייצג אזורים עם מאפיינים סביבתיים דומים ל-100 מיקומים אקראיים שבהם יש נוכחות, ואילו האשכול השני ייצג אזורים עם מאפיינים שונים.
יצירת נתוני פסאודו-היעדרות בתוך אשכולות שונים: בתוך האשכול השני שזוהה בשלב הראשון (שיש לו מאפיינים סביבתיים שונים מנתוני הנוכחות), ייווצרו נקודות פסאודו-היעדרות שנוצרו באופן אקראי. הנקודות האלה של פסאודו-היעדרות ייצגו מיקומים שבהם לא צפוי שהמין יתקיים.

# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
    collection=data.randomColumn().sort('random').limit(100),
    properties=[],
    scale=grain_size
)

# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
    nClusters=2,
    distanceFunction="Euclidean"
).train(pvals)

cl_result = predictors.cluster(clusterer)

# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
    collection=data.randomColumn().sort('random').limit(200),
    properties=[],
    scale=grain_size
)

# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)

# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
            grain_size).mask().neq(1).selfMask()

# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)

# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map

התאמת המודל וחיזוי

עכשיו נחלק את הנתונים לנתוני אימון ולנתוני בדיקה. נתוני האימון ישמשו לאימון המודל כדי למצוא את הפרמטרים האופטימליים, ונתוני הבדיקה ישמשו להערכת המודל שאומן קודם לכן. מושג חשוב שצריך לקחת בחשבון בהקשר הזה הוא אוטוקורלציה מרחבית.

אוטוקורלציה מרחבית היא רכיב חיוני ב-SDM, שקשור לחוק של טובלר. הוא מגלם את הרעיון ש "הכול קשור להכול, אבל פריטים קרובים קשורים יותר מפריטים רחוקים". אוטוקורלציה מרחבית מייצגת את הקשר המשמעותי בין מיקום המינים לבין משתנים סביבתיים. עם זאת, אם קיים מתאם מרחבי אוטומטי בין נתוני האימון לבין נתוני הבדיקה, יכול להיות שהעצמאות בין שתי קבוצות הנתונים תיפגע. הדבר משפיע באופן משמעותי על הערכת יכולת ההכללה של המודל.

אחת מהשיטות לפתרון הבעיה הזו היא טכניקת אימות צולב של בלוקים מרחביים, שכוללת חלוקה של הנתונים למערכי נתונים של אימון ובדיקה. הטכניקה הזו כוללת חלוקה של הנתונים לכמה בלוקים, ושימוש בכל בלוק באופן עצמאי כמערך נתונים לאימון ולבדיקה, כדי לצמצם את ההשפעה של קורלציה מרחבית. כך משפרים את העצמאות בין מערכי הנתונים, ומאפשרים הערכה מדויקת יותר של יכולת ההכללה של המודל.

הנה התהליך הספציפי:

יצירת בלוקים מרחביים: חלוקת מערך הנתונים כולו לבלוקים מרחביים בגודל שווה (למשל, ‫50x50 ק"מ).
הקצאה של קבוצות אימון ובדיקה: כל בלוק מרחבי מוקצה באופן אקראי לקבוצת האימון (70%) או לקבוצת הבדיקה (30%). כך המודל לא מתאים יתר על המידה לנתונים מאזורים ספציפיים, והתוצאות יהיו כלליות יותר.
אימות צולב איטרטיבי: התהליך כולו חוזר על עצמו n פעמים (למשל, ‫10 פעמים). בכל איטרציה, הבלוקים מחולקים שוב באופן אקראי למערכי אימון ולמערכי בדיקה, במטרה לשפר את היציבות והאמינות של המודל.
יצירת נתוני פסאודו-היעדרות: בכל איטרציה, נתוני פסאודו-היעדרות נוצרים באופן אקראי כדי להעריך את הביצועים של המודל.

Scale = 50000
grid = watermask.reduceRegions(
    collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
    reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))

Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map

עכשיו אפשר להתאים את המודל. התאמת מודל כוללת הבנה של הדפוסים בנתונים והתאמה של הפרמטרים של המודל (משקלים והטיות) בהתאם. התהליך הזה מאפשר למודל לספק תחזיות מדויקות יותר כשמוצגים לו נתונים חדשים. לשם כך, הגדרנו פונקציה בשם SDM()‎ שתתאים למודל.

אנחנו נשתמש באלגוריתם Random Forest.

def sdm(x):
    seed = ee.Number(x)

    # Random block division for training and validation
    rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
    training_grid = rand_blk.filter(ee.Filter.lt("random", split))  # Grid for training
    testing_grid = rand_blk.filter(ee.Filter.gte("random", split))  # Grid for testing

    # Presence points
    presence_points = ee.FeatureCollection(data)
    presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
    tr_presence_points = presence_points.filter(
        ee.Filter.bounds(training_grid)
    )  # Presence points for training
    te_presence_points = presence_points.filter(
        ee.Filter.bounds(testing_grid)
    )  # Presence points for testing

    # Pseudo-absence points for training
    tr_pseudo_abs_points = area_for_pa.sample(
        region=training_grid,
        scale=grain_size,
        numPixels=tr_presence_points.size().add(300),
        seed=seed,
        geometries=True,
    )
    # Same number of pseudo-absence points as presence points for training
    tr_pseudo_abs_points = (
        tr_pseudo_abs_points.randomColumn()
        .sort("random")
        .limit(ee.Number(tr_presence_points.size()))
    )
    tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))

    te_pseudo_abs_points = area_for_pa.sample(
        region=testing_grid,
        scale=grain_size,
        numPixels=te_presence_points.size().add(100),
        seed=seed,
        geometries=True,
    )
    # Same number of pseudo-absence points as presence points for testing
    te_pseudo_abs_points = (
        te_pseudo_abs_points.randomColumn()
        .sort("random")
        .limit(ee.Number(te_presence_points.size()))
    )
    te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))

    # Merge training and pseudo-absence points
    training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
    testing_partition = te_presence_points.merge(te_pseudo_abs_points)

    # Extract predictor variable values at training points
    train_pvals = predictors.sampleRegions(
        collection=training_partition,
        properties=["PresAbs"],
        scale=grain_size,
        geometries=True,
    )

    # Random Forest classifier
    classifier = ee.Classifier.smileRandomForest(
        numberOfTrees=500,
        variablesPerSplit=None,
        minLeafPopulation=10,
        bagFraction=0.5,
        maxNodes=None,
        seed=seed,
    )
    # Presence probability: Habitat suitability map
    classifier_pr = classifier.setOutputMode("PROBABILITY").train(
        train_pvals, "PresAbs", bands
    )
    classified_img_pr = predictors.select(bands).classify(classifier_pr)

    # Binary presence/absence map: Potential distribution map
    classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
        train_pvals, "PresAbs", bands
    )
    classified_img_bin = predictors.select(bands).classify(classifier_bin)

    return [
        classified_img_pr,
        classified_img_bin,
        training_partition,
        testing_partition,
    ], classifier_pr

הבלוקים המרחביים מחולקים ל-70% לאימון המודל ו-30% לבדיקת המודל, בהתאמה. נתוני פסאודו-היעדרות נוצרים באופן אקראי בכל קבוצת אימון ובדיקה בכל איטרציה. כתוצאה מכך, כל הרצה מניבה קבוצות שונות של נתוני נוכחות ופסאודו-נוכחות לאימון ולבדיקה של המודל.

split = 0.7
numiter = 10

# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)

# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]

results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list

for item in items:
    result, trained = sdm(item)
    # Accumulate SDM results into the list
    results_list.extend(result)

    # Accumulate variable importance into the list
    importance = ee.Dictionary(trained.explain()).get('importance')
    importances_list.extend(importance.getInfo().items())

# Flatten the SDM results list
results = ee.List(results_list).flatten()

עכשיו אפשר לראות את מפת ההתאמה לבית הגידול ואת מפת התפוצה הפוטנציאלית של פיטה פיות. במקרה הזה, מפת ההתאמה לבית הגידול נוצרת באמצעות הפונקציה mean() כדי לחשב את הממוצע של כל מיקום פיקסל בכל התמונות, ומפת ההפצה הפוטנציאלית נוצרת באמצעות הפונקציה mode() כדי לקבוע את הערך שמופיע הכי הרבה פעמים בכל מיקום פיקסל בכל התמונות.

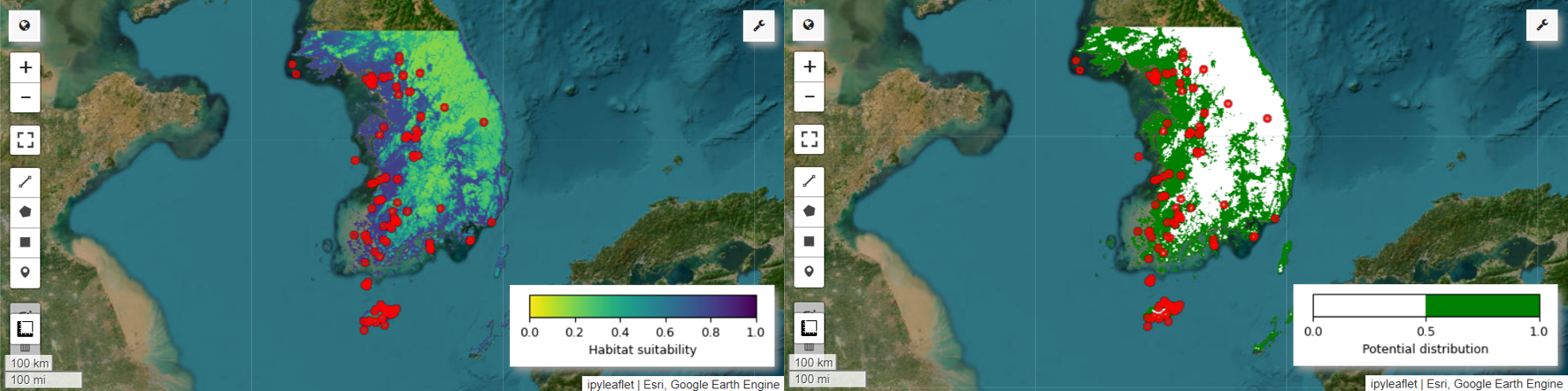
תוצאות SDM

# Habitat suitability map
images = ee.List.sequence(
    0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
    lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()

Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')

vis_params = {
    'min': 0,
    'max': 1,
    'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
                 orientation="horizontal",
                 layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map

# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
    lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()

Map = geemap.Map(
    layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)

vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
    vis_params,
    label="Potential distribution",
    discrete=True,
    orientation="horizontal",
    layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map

חשיבות המשתנים והערכת הדיוק

‫Random Forest (ee.Classifier.smileRandomForest) היא אחת משיטות הלמידה של קבוצות, שפועלת על ידי בנייה של כמה עצי החלטה כדי לבצע תחזיות. כל עץ החלטה לומד באופן עצמאי מקבוצות משנה שונות של הנתונים, והתוצאות שלהם מצטברות כדי לאפשר תחזיות מדויקות ויציבות יותר.

חשיבות המשתנה היא מדד שמעריך את ההשפעה של כל משתנה על התחזיות במודל Random Forest. נשתמש ב-importances_list שהוגדר קודם כדי לחשב ולהדפיס את החשיבות הממוצעת של המשתנה.

def plot_variable_importance(importances_list):
    # Extract each variable importance value into a list
    variables = [item[0] for item in importances_list]
    importances = [item[1] for item in importances_list]

    # Calculate the average importance for each variable
    average_importances = {}
    for variable in set(variables):
        indices = [i for i, var in enumerate(variables) if var == variable]
        average_importance = np.mean([importances[i] for i in indices])
        average_importances[variable] = average_importance

    # Sort the importances in descending order of importance
    sorted_importances = sorted(average_importances.items(),
                                key=lambda x: x[1], reverse=False)
    variables = [item[0] for item in sorted_importances]
    avg_importances = [item[1] for item in sorted_importances]

    # Adjust the graph size
    plt.figure(figsize=(8, 4))

    # Plot the average importance as a horizontal bar chart
    plt.barh(variables, avg_importances)
    plt.xlabel('Importance')
    plt.ylabel('Variables')
    plt.title('Average Variable Importance')

    # Display values above the bars
    for i, v in enumerate(avg_importances):
        plt.text(v + 0.02, i, f"{v:.2f}", va='center')

    # Adjust the x-axis range
    plt.xlim(0, max(avg_importances) + 5)  # Adjust to the desired range

    plt.tight_layout()
    plt.savefig('variable_importance.png')
    plt.show()

plot_variable_importance(importances_list)

אנחנו משתמשים בנתונים של קבוצות הבדיקה כדי לחשב את הערכים של AUC-ROC ו-AUC-PR לכל הרצה. לאחר מכן, אנחנו מחשבים את הממוצע של AUC-ROC ו-AUC-PR על פני n איטרציות.

AUC-ROC מייצג את השטח מתחת לעקומה של התרשים 'רגישות (Recall) לעומת 1-ספציפיות', וממחיש את הקשר בין הרגישות לבין הספציפיות כשהסף משתנה. הספציפיות מבוססת על כל המקרים שלא התרחשו. לכן, ה-AUC-ROC כולל את כל הרבעים של מטריצת השגיאות.

AUC-PR מייצג את השטח שמתחת לעקומה של הגרף 'דיוק לעומת היזכרות (רגישות)', שבו מוצג הקשר בין דיוק לבין היזכרות כשהסף משתנה. הדיוק מבוסס על כל המקרים החזויים. לכן, מדד AUC-PR לא כולל את הערכים השליליים האמיתיים (TN).

הערה: חשוב לוודא שלכל הרצה יש מספר מספיק של נקודות לאימות המודל. יכול להיות שמספר הנקודות הסופי יהיה שונה בגלל החלוקה האקראית של בלוקים מרחביים, ולכן חשוב לוודא שיש מספיק נקודות נוכחות ונקודות פסאודו-היעדרות לאימות המודל. במקרה של מינים בסכנת הכחדה או מינים נדירים, יכול להיות שיהיה מחסור בנתוני התרחשות, מה שיוביל למערך נתונים לא מספיק לבדיקה. במקרים כאלה, חלופות יכולות לכלול איסוף נתונים נוסף שמבוסס על ידע וניסיון של מומחים, או שימוש במקורות נתונים חלופיים רלוונטיים.

def print_pres_abs_sizes(TestingDatasets, numiter):
    # Check and print the sizes of presence and pseudo-absence coordinates
    def get_pres_abs_size(x):
        fc = ee.FeatureCollection(TestingDatasets.get(x))
        presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
        pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
        return ee.List([presence_size, pseudo_absence_size])

    sizes_info = (
        ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
        .map(get_pres_abs_size)
        .getInfo()
    )

    for i, sizes in enumerate(sizes_info):
        presence_size = sizes[0]
        pseudo_absence_size = sizes[1]
        print(
            f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
        )

# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
    3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))

print_pres_abs_sizes(testing_datasets, numiter)

def get_acc(hsm, t_data, grain_size):
    pr_prob_vals = hsm.sampleRegions(
        collection=t_data, properties=["PresAbs"], scale=grain_size
    )
    seq = ee.List.sequence(start=0, end=1, count=25)  # Divide 0 to 1 into 25 intervals

    def calculate_metrics(cutoff):
        # Each element of the seq list is passed as cutoff(threshold value)

        # Observed present = TP + FN
        pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)

        # TP (True Positive)
        tp = ee.Number(
            pres.filterMetadata("classification", "greater_than", cutoff).size()
        )

        # TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
        tpr = tp.divide(pres.size())

        # Observed absent = FP + TN
        abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)

        # FN (False Negative)
        fn = ee.Number(
            pres.filterMetadata("classification", "less_than", cutoff).size()
        )

        # TNR (True Negative Rate) = Specificity = TN  / (FP + TN) = TN / Observed absent
        tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
        tnr = tn.divide(abs.size())

        # FP (False Positive)
        fp = ee.Number(
            abs.filterMetadata("classification", "greater_than", cutoff).size()
        )

        # FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
        fpr = fp.divide(abs.size())

        # Precision = TP / (TP + FP) = TP / Predicted present
        precision = tp.divide(tp.add(fp))

        # SUMSS = SUM of Sensitivity and Specificity
        sumss = tpr.add(tnr)

        return ee.Feature(
            None,
            {
                "cutoff": cutoff,
                "TP": tp,
                "TN": tn,
                "FP": fp,
                "FN": fn,
                "TPR": tpr,
                "TNR": tnr,
                "FPR": fpr,
                "Precision": precision,
                "SUMSS": sumss,
            },
        )

    return ee.FeatureCollection(seq.map(calculate_metrics))

def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
    # Calculate AUC-ROC and AUC-PR
    def calculate_auc_metrics(x):
        hsm = ee.Image(images.get(x))
        t_data = ee.FeatureCollection(testing_datasets.get(x))
        acc = get_acc(hsm, t_data, grain_size)

        # Calculate AUC-ROC
        x = ee.Array(acc.aggregate_array("FPR"))
        y = ee.Array(acc.aggregate_array("TPR"))
        x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
        y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
        auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)

        # Calculate AUC-PR
        x = ee.Array(acc.aggregate_array("TPR"))
        y = ee.Array(acc.aggregate_array("Precision"))
        x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
        y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
        auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)

        return (auc_roc, auc_pr)

    auc_metrics = (
        ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
        .map(calculate_auc_metrics)
        .getInfo()
    )

    # Print AUC-ROC and AUC-PR for each iteration
    df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
    df.index = [f"Iteration {i + 1}" for i in range(len(df))]
    df.to_csv("auc_metrics.csv", index_label="Iteration")
    print(df)

    # Calculate mean and standard deviation of AUC-ROC and AUC-PR
    mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
    mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
    print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
    print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")

%%time

# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)

במדריך הזה הצגנו דוגמה מעשית לשימוש ב-Google Earth Engine ‏ (GEE) למידול של תפוצת מינים (SDM). נקודה חשובה היא הרבגוניות והגמישות של GEE בתחום של SDM. היכולות המתקדמות של Earth Engine לעיבוד נתונים גיאוספציאליים פותחות בפני חוקרים ופעילי שמירת טבע אפשרויות בלתי מוגבלות להבנה ולשמירה של המגוון הביולוגי בכדור הארץ. הידע והכישורים שרוכשים בעזרת המדריך הזה מאפשרים לאנשים לחקור את תחום המחקר האקולוגי המרתק הזה ולתרום לו.

בניית מודלים של התפלגות מינים קל לארגן דפים בעזרת אוספים אפשר לשמור ולסווג תוכן על סמך ההעדפות שלך.

תפעיל אותי קודם

סקירה כללית קצרה של מידול של תפוצת מינים

מהו מידול של תפוצת מינים?

הנתונים שנדרשים ל-SDM

תהליך העבודה של SDM באמצעות GEE

חיזוי וניתוח של בתי גידול באמצעות GEE

איסוף ועיבוד מקדים של נתוני מיקום של מינים

הגדרה של אזור העניין

הוספה של משתני סביבה של GEE

יצירה של נתוני היעדרות פסאודו

התאמת המודל וחיזוי

חשיבות המשתנים והערכת הדיוק

בניית מודלים של התפלגות מינים