이 튜토리얼에서는 Google Earth Engine을 사용한 종 분포 모델링의 방법론을 소개합니다. 종 분포 모델링에 관한 간략한 개요가 제공된 후, 멸종 위기에 처한 조류 종인 요정비둘기 (학명: Pitta nympha)의 서식지를 예측하고 분석하는 프로세스가 이어집니다.
먼저 실행
다음 셀을 실행하여 API를 초기화합니다. 출력에는 계정을 사용하여 이 노트북에 Earth Engine 액세스 권한을 부여하는 방법에 관한 안내가 포함됩니다.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
종 분포 모델링에 관한 간략한 개요
종 분포 모델이 무엇인지, Google Earth Engine을 사용하여 처리하는 이점, 모델에 필요한 데이터, 워크플로가 어떻게 구성되는지 살펴보겠습니다.
종 분포 모델링이란 무엇인가요?
종 분포 모델링 (아래 SDM)은 종의 실제 또는 잠재적 지리적 분포를 추정하는 데 사용되는 가장 일반적인 방법입니다. 특정 종에 적합한 환경 조건을 특징화한 다음 이러한 적합한 조건이 지리적으로 분포하는 위치를 식별하는 작업이 포함됩니다.
SDM은 최근 몇 년간 보존 계획의 중요한 구성요소로 부상했으며, 이를 위해 다양한 모델링 기법이 개발되었습니다. Google Earth Engine (GEE)에서 SDM을 구현하면 대규모 환경 데이터에 쉽게 액세스할 수 있을 뿐만 아니라 강력한 컴퓨팅 기능과 머신러닝 알고리즘 지원을 통해 신속한 모델링이 가능합니다.
SDM에 필요한 데이터
SDM은 일반적으로 알려진 종 발생 기록과 환경 변수 간의 관계를 활용하여 개체군이 유지될 수 있는 조건을 식별합니다. 즉, 두 가지 유형의 모델 입력 데이터가 필요합니다.
- 알려진 종의 출현 기록
- 다양한 환경 변수
이 데이터는 종의 존재와 관련된 환경 조건을 식별하기 위해 알고리즘에 입력됩니다.
GEE를 사용하는 SDM 워크플로
GEE를 사용하는 SDM의 워크플로는 다음과 같습니다.
- 종 발생 데이터 수집 및 전처리
- 관심 영역 정의
- GEE 환경 변수 추가
- 의사 부재 데이터 생성
- 모델 적합 및 예측
- 변수 중요도 및 정확도 평가
GEE를 사용한 서식지 예측 및 분석
요정물총새 (Pitta nympha)가 GEE 기반 SDM의 적용을 보여주는 사례 연구로 사용됩니다. 이 특정 종은 한 가지 예로 선택되었지만 연구자는 제공된 소스 코드를 약간 수정하여 관심 있는 모든 대상 종에 이 방법을 적용할 수 있습니다.
팔색조는 한국에서 희귀한 여름 철새이자 통과 철새로, 최근 한반도 기후 온난화로 인해 분포 지역이 확대되고 있습니다. 희귀종, 멸종 위기 야생 동식물 2급, 천연기념물 제204호로 분류되며, 국가 적색 목록에서 지역 멸종 (RE)으로 평가되고 IUCN 카테고리에 따라 취약 (VU)으로 평가됩니다.
요정물총새의 보전 계획을 위해 SDM을 수행하는 것은 매우 유용한 것으로 보입니다. 이제 GEE를 통해 서식지 예측 및 분석을 진행해 보겠습니다.
먼저 Python 라이브러리를 가져옵니다.import 문은 모듈의 전체 콘텐츠를 가져오고 from import 문은 모듈에서 특정 객체를 가져올 수 있도록 합니다.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
종 발생 데이터 수집 및 전처리
이제 요정물총새의 출현 데이터를 수집해 보겠습니다. 현재 관심 있는 종의 출현 데이터에 액세스할 수 없는 경우에도 GBIF API를 통해 특정 종에 관한 관찰 데이터를 얻을 수 있습니다. GBIF API는 GBIF에서 제공하는 종 분포 데이터에 액세스할 수 있는 인터페이스로, 사용자가 데이터를 검색, 필터링, 다운로드하고 종과 관련된 다양한 정보를 획득할 수 있습니다.
아래 코드에서 species_name 변수에는 종의 학명 (예: Pitta nympha(요정물총새)와 같은 종 이름이 할당되고 country_code 변수에는 국가 코드(예: 대한민국은 KR). base_url 변수는 GBIF API의 주소를 저장합니다. params는 API 요청에 사용될 매개변수가 포함된 사전입니다.
scientificName: 검색할 종의 학명을 설정합니다.country: 특정 국가로 검색을 제한합니다.hasCoordinate: 좌표가 있는 데이터만 검색되도록 합니다 (true).basisOfRecord: 사람의 관찰 기록 (HUMAN_OBSERVATION)만 선택합니다.limit: 반환되는 최대 결과 수를 10000으로 설정합니다.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
이전에 설정한 매개변수를 사용하여 GBIF API에서 요정물총새 (Pitta nympha)의 관찰 기록을 쿼리하고 결과를 DataFrame에 로드하여 첫 번째 행을 확인합니다. DataFrame은 행과 열로 구성된 테이블 형식 데이터를 처리하기 위한 데이터 구조입니다. 필요한 경우 DataFrame을 CSV 파일로 저장하고 다시 읽을 수 있습니다.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
다음으로 DataFrame을 지리 정보 (geometry) 열이 포함된 GeoDataFrame으로 변환하고 첫 번째 행을 확인합니다. GeoDataFrame은 GeoPackage 파일 (*.gpkg)로 저장하고 다시 읽을 수 있습니다.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
이번에는 GeoDataFrame에서 연도 및 월별 데이터 분포를 시각화하고 그래프로 표시하는 함수를 만들었습니다. 이 그래프는 이미지 파일로 저장할 수 있습니다. 히트맵을 사용하면 연도별, 월별 종 발생 빈도를 빠르게 파악할 수 있어 데이터 내 시간적 변화와 패턴을 직관적으로 시각화할 수 있습니다. 이를 통해 종 발생 데이터의 시간적 패턴과 계절적 변동을 파악할 수 있을 뿐만 아니라 데이터 내 이상치 또는 품질 문제를 신속하게 감지할 수 있습니다.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
1995년 데이터는 다른 해에 비해 매우 희소하고 상당한 격차가 있으며, 8월과 9월도 샘플이 제한적이고 다른 기간과 비교해 다른 계절적 특성을 보입니다. 이 데이터를 제외하면 모델의 안정성과 예측력이 향상될 수 있습니다.
하지만 데이터를 제외하면 모델의 일반화 능력이 향상될 수 있지만 연구 목표와 관련된 중요한 정보가 손실될 수도 있습니다. 따라서 이러한 결정은 신중하게 고려해야 합니다.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
이제 필터링된 GeoDataFrame이 Google Earth Engine 객체로 변환됩니다.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
다음으로 SDM 결과의 래스터 픽셀 크기를 1km 해상도로 정의합니다.
# Spatial resolution setting (meters)
grain_size = 1000
동일한 1km 해상도 래스터 픽셀 내에 여러 발생 지점이 있는 경우 동일한 지리적 위치에서 동일한 환경 조건을 공유할 가능성이 높습니다. 분석에서 이러한 데이터를 직접 사용하면 결과에 편향이 발생할 수 있습니다.
즉, 지역 샘플링 편향의 잠재적 영향을 제한해야 합니다. 이를 위해 각 1km 픽셀 내에 한 위치만 유지하고 다른 모든 위치를 삭제하여 모델이 환경 조건을 더 객관적으로 반영할 수 있도록 합니다.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
전처리 전 (파란색)과 전처리 후 (빨간색)의 지리적 샘플링 편향을 비교하는 시각화는 아래에 표시되어 있습니다. 비교를 용이하게 하기 위해 지도는 한라산 국립공원에서 팔색조 발생 좌표가 많이 분포된 지역을 중심으로 표시됩니다.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
관심 영역 정의
관심 영역 (아래 AOI) 정의는 연구자가 분석하려는 지리적 영역을 나타내기 위해 사용하는 용어를 의미합니다. '연구 지역'이라는 용어와 유사한 의미를 갖습니다.
이 컨텍스트에서 발생 지점 레이어 지오메트리의 경계 상자를 가져와 AOI를 정의하기 위해 주변에 50km 버퍼 (최대 허용 오차 1,000m)를 만들었습니다.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
GEE 환경 변수 추가
이제 분석에 환경 변수를 추가해 보겠습니다. GEE는 온도, 강수량, 고도, 토지 피복, 지형과 같은 환경 변수에 대한 다양한 데이터 세트를 제공합니다. 이러한 데이터 세트를 통해 요정물총새의 서식지 선호도에 영향을 미칠 수 있는 다양한 요인을 종합적으로 분석할 수 있습니다.
SDM에서 GEE 환경 변수를 선택할 때는 종의 서식지 선호도 특성을 반영해야 합니다. 이를 위해서는 요정물총새의 서식지 선호도에 관한 사전 연구와 문헌 검토가 필요합니다. 이 튜토리얼에서는 주로 GEE를 사용하는 SDM의 워크플로에 중점을 두므로 일부 세부정보는 생략됩니다.
WorldClim V1 Bioclim: 이 데이터 세트는 월별 온도 및 강수량 데이터에서 파생된 19개의 생기후 변수를 제공합니다. 1960년부터 1991년까지의 기간을 다루며 해상도는 927.67m입니다.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM 디지털 고도 30m: 이 데이터 세트에는 셔틀 레이더 지형 임무 (SRTM)의 디지털 고도 데이터가 포함되어 있습니다. 이 데이터는 주로 2000년경에 수집되었으며 약 30미터 (1초)의 해상도로 제공됩니다. 다음 코드는 SRTM 데이터에서 고도, 경사, 경사면, 음영 레이어를 계산합니다.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: Landsat의 Vegetation Continuous Fields (VCF) 데이터 세트는 식물 높이가 5m를 초과할 때 수직으로 투영된 식물 피복 비율을 추정합니다. 이 데이터 세트는 2000년, 2005년, 2010년, 2015년을 중심으로 4개 기간에 대해 30m 해상도로 제공됩니다. 여기서는 이 네 기간의 중앙값이 사용됩니다.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (생기후 변수), terrain (지형), median_tcc (나무 덮개)이 단일 멀티밴드 이미지로 결합됩니다. elevation 대역이 terrain에서 선택되고 elevation이 0보다 큰 위치에 대해 watermask가 생성됩니다. 이렇게 하면 해수면 아래 지역 (예: 바다)이 마스크 처리되어 연구자가 AOI의 다양한 환경 요인을 포괄적으로 분석할 수 있습니다.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
상관관계가 높은 예측 변수가 모델에 함께 포함되면 다중공선성 문제가 발생할 수 있습니다. 다중 공선성은 모델의 독립 변수 간에 강력한 선형 관계가 있어 모델의 계수 (가중치) 추정치가 불안정해지는 현상입니다. 이러한 불안정성으로 인해 모델의 신뢰성이 떨어지고 새로운 데이터에 대한 예측이나 해석이 어려워질 수 있습니다. 따라서 다중 공선성을 고려하여 예측 변수를 선택하는 과정을 진행합니다.
먼저 5,000개의 임의 포인트를 생성한 다음 해당 포인트에서 단일 멀티밴드 이미지의 예측 변수 값을 추출합니다.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
각 포인트에 대해 추출된 예측 변수 값을 DataFrame으로 변환한 다음 첫 번째 행을 확인합니다.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
지정된 예측 변수 간의 스피어만 상관 계수를 계산하고 이를 히트맵으로 시각화합니다.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
스피어만 상관 계수는 예측 변수 간의 일반적인 연관성을 이해하는 데 유용하지만 여러 변수가 상호작용하는 방식을 직접 평가하지는 않으며 다중 공선성을 감지하지도 않습니다.
분산 확대 계수 (아래 VIF)는 다중 공선성을 평가하고 변수 선택을 안내하는 데 사용되는 통계 측정항목입니다. 각 독립 변수와 다른 독립 변수 간의 선형 관계 정도를 나타내며 VIF 값이 높으면 다중 공선성이 있다는 증거가 될 수 있습니다.
일반적으로 VIF 값이 5 또는 10을 초과하면 변수가 다른 변수와 강한 상관관계가 있어 모델의 안정성과 해석 가능성이 저하될 수 있음을 나타냅니다. 이 튜토리얼에서는 변수 선택에 VIF 값이 10 미만이라는 기준을 사용했습니다. 다음 6개 변수는 VIF를 기반으로 선택되었습니다.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
이제 선택한 6개의 예측 변수를 지도에 시각화해 보겠습니다.
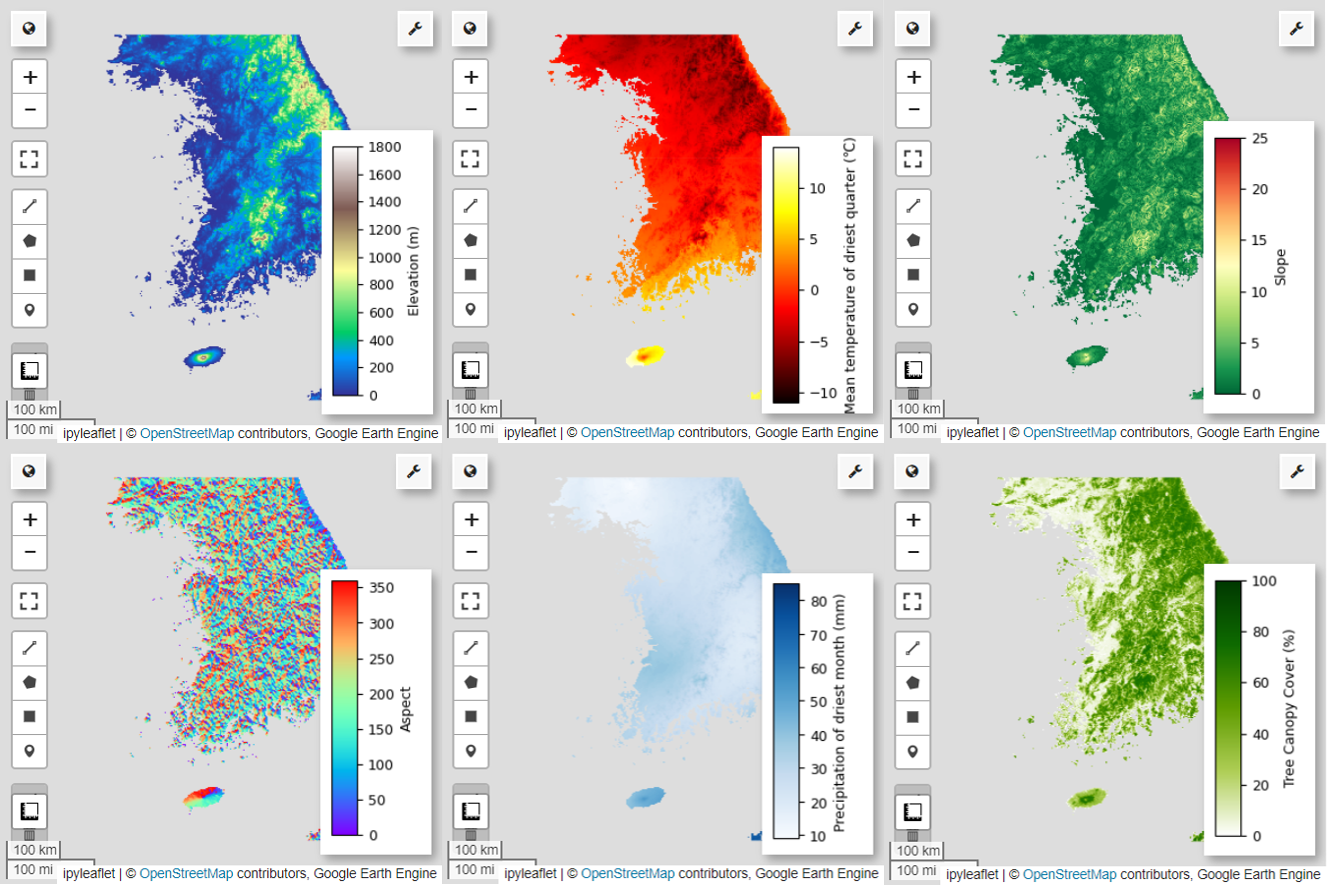
다음 코드를 사용하여 지도 시각화에 사용할 수 있는 팔레트를 살펴볼 수 있습니다. 예를 들어 terrain 팔레트는 다음과 같습니다.
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
의사 부재 데이터 생성
SDM 과정에서 종의 입력 데이터 선택은 주로 다음 두 가지 방법을 사용하여 접근합니다.
출현-배경 방법: 이 방법은 특정 종이 관찰된 위치 (출현)를 해당 종이 관찰되지 않은 다른 위치 (배경)와 비교합니다. 여기서 배경 데이터는 종이 존재하지 않는 영역을 의미하는 것이 아니라 연구 지역의 전반적인 환경 조건을 반영하도록 설정됩니다. 이 값은 종이 서식할 수 있는 적합한 환경과 그렇지 않은 환경을 구분하는 데 사용됩니다.
유무 방법: 이 방법은 종이 관찰된 위치 (유)와 종이 관찰되지 않은 위치 (무)를 비교합니다. 여기서 부재 데이터는 종이 존재하지 않는 것으로 알려진 특정 위치를 나타냅니다. 연구 지역의 전반적인 환경 조건을 반영하는 것이 아니라 종이 존재하지 않는 것으로 추정되는 위치를 나타냅니다.
실제로 실제 부재 데이터를 수집하기 어려운 경우가 많으므로 인위적으로 생성된 유사 부재 데이터가 자주 사용됩니다. 하지만 인위적으로 생성된 의사 부재 지점이 실제 부재 영역을 정확하게 반영하지 않을 수 있으므로 이 방법의 한계와 잠재적 오류를 인지하는 것이 중요합니다.
이 두 가지 방법 중 어떤 방법을 선택할지는 데이터 가용성, 연구 목표, 모델 정확도 및 신뢰성, 시간 및 리소스에 따라 달라집니다. 여기서는 GBIF에서 수집한 출현 데이터와 인위적으로 생성된 의사 부재 데이터를 사용하여 '출현-부재' 방법을 사용하여 모델링합니다.
의사 부재 데이터 생성은 '환경 프로파일링 접근 방식'을 통해 이루어지며 구체적인 단계는 다음과 같습니다.
k-평균 클러스터링을 사용한 환경 분류: 유클리드 거리를 기반으로 하는 k-평균 클러스터링 알고리즘을 사용하여 연구 지역 내의 픽셀을 두 개의 클러스터로 나눕니다. 한 클러스터는 무작위로 선택된 100개의 위치와 환경적 특성이 유사한 영역을 나타내고 다른 클러스터는 특성이 다른 영역을 나타냅니다.
유사하지 않은 클러스터 내에서 의사 부재 데이터 생성: 첫 번째 단계에서 식별된 두 번째 클러스터 (환경적 특성이 존재 데이터와 다름) 내에서 무작위로 생성된 의사 부재 포인트가 생성됩니다. 이러한 의사 부재 포인트는 종이 존재하지 않을 것으로 예상되는 위치를 나타냅니다.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
모델 적합 및 예측
이제 데이터를 학습 데이터와 테스트 데이터로 나눕니다. 학습 데이터는 모델을 학습시켜 최적의 매개변수를 찾는 데 사용되고 테스트 데이터는 사전에 학습된 모델을 평가하는 데 사용됩니다. 이 맥락에서 고려해야 할 중요한 개념은 공간적 자기상관입니다.
공간적 자기상관은 토블러의 법칙과 관련된 SDM의 필수 요소입니다. '모든 것은 서로 관련이 있지만 가까운 것은 먼 것보다 더 관련이 있다'는 개념을 구현합니다. 공간 자기상관은 종의 위치와 환경 변수 간의 유의미한 관계를 나타냅니다. 하지만 학습 데이터와 테스트 데이터 간에 공간 자기 상관이 있는 경우 두 데이터 세트 간의 독립성이 손상될 수 있습니다. 이는 모델의 일반화 기능 평가에 상당한 영향을 미칩니다.
이 문제를 해결하는 한 가지 방법은 데이터를 학습 및 테스트 데이터 세트로 나누는 공간 블록 교차 검증 기법입니다. 이 기법은 데이터를 여러 블록으로 나누고 각 블록을 독립적으로 학습 및 테스트 데이터 세트로 사용하여 공간 자기 상관의 영향을 줄입니다. 이렇게 하면 데이터 세트 간의 독립성이 향상되어 모델의 일반화 능력을 더 정확하게 평가할 수 있습니다.
구체적인 절차는 다음과 같습니다.
- 공간 블록 생성: 전체 데이터 세트를 크기가 동일한 공간 블록으로 나눕니다 (예: 50x50 km).
- 학습 세트 및 테스트 세트 할당: 각 공간 블록은 학습 세트 (70%) 또는 테스트 세트 (30%)에 무작위로 할당됩니다. 이렇게 하면 모델이 특정 영역의 데이터에 과적합되는 것을 방지하고 더 일반화된 결과를 얻을 수 있습니다.
- 반복 교차 검증: 전체 프로세스가 n회 반복됩니다 (예: 10회) 각 반복에서 블록은 학습 세트와 테스트 세트로 다시 무작위로 나뉘며, 이는 모델의 안정성과 신뢰성을 개선하기 위한 것입니다.
- 의사 부재 데이터 생성: 각 반복에서 모델의 성능을 평가하기 위해 의사 부재 데이터가 무작위로 생성됩니다.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
이제 모델을 적합시킬 수 있습니다. 모델 피팅에는 데이터의 패턴을 이해하고 그에 따라 모델의 파라미터 (가중치 및 편향)를 조정하는 작업이 포함됩니다. 이 프로세스를 통해 모델은 새로운 데이터가 제공될 때 더 정확한 예측을 할 수 있습니다. 이를 위해 모델을 적합시키는 SDM()이라는 함수를 정의했습니다.
Random Forest 알고리즘을 사용합니다.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
공간 블록은 각각 모델 학습용 70% 와 모델 테스트용 30% 로 나뉩니다. 의사 부재 데이터는 매 반복에서 각 학습 및 테스트 세트 내에서 무작위로 생성됩니다. 따라서 각 실행은 모델 학습 및 테스트를 위해 서로 다른 출석 및 의사 부재 데이터 세트를 생성합니다.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
이제 요정물총새의 서식지 적합성 지도와 잠재적 분포 지도를 시각화할 수 있습니다. 이 경우 mean() 함수를 사용하여 모든 이미지에서 각 픽셀 위치의 평균을 계산하여 서식지 적합성 지도를 만들고, mode() 함수를 사용하여 모든 이미지에서 각 픽셀 위치에서 가장 자주 발생하는 값을 확인하여 잠재적 분포 지도를 생성합니다.
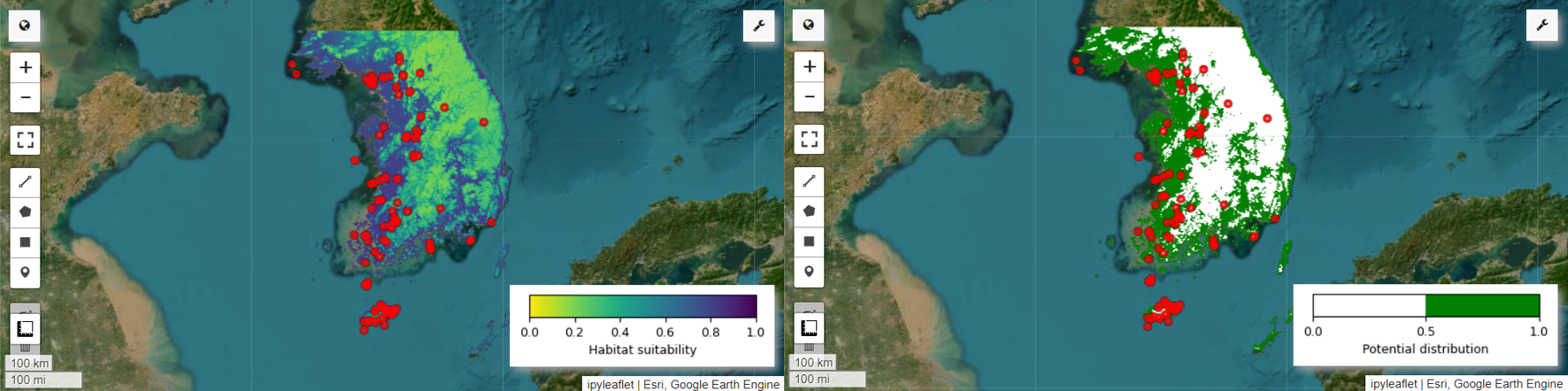
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
변수 중요도 및 정확도 평가
랜덤 포레스트 (ee.Classifier.smileRandomForest)는 여러 결정 트리를 구성하여 예측하는 앙상블 학습 방법 중 하나입니다. 각 결정 트리는 데이터의 서로 다른 하위 집합에서 독립적으로 학습하며, 결과를 집계하여 더 정확하고 안정적인 예측을 할 수 있습니다.
변수 중요도는 랜덤 포레스트 모델 내에서 각 변수가 예측에 미치는 영향을 평가하는 측정치입니다. 이전에 정의한 importances_list를 사용하여 평균 변수 중요도를 계산하고 출력합니다.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
테스트 데이터 세트를 사용하여 각 실행의 AUC-ROC와 AUC-PR을 계산합니다. 그런 다음 n번의 반복에 걸쳐 평균 AUC-ROC와 AUC-PR을 계산합니다.
AUC-ROC는 '민감도 (재현율) 대 1-특이도' 그래프의 곡선 아래 영역을 나타내며, 임계값이 변경될 때 민감도와 특이도 간의 관계를 보여줍니다. 특이성은 관찰된 모든 비발생을 기반으로 합니다. 따라서 AUC-ROC는 혼동 행렬의 모든 사분면을 포함합니다.
AUC-PR은 '정밀도 대 재현율 (민감도)' 그래프의 곡선 아래 면적을 나타내며, 임계값이 변함에 따라 정밀도와 재현율 간의 관계를 보여줍니다. 정밀도는 예측된 모든 발생을 기반으로 합니다. 따라서 AUC-PR에는 실제 음성 (TN)이 포함되지 않습니다.
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
이 튜토리얼에서는 종 분포 모델링 (SDM)에 Google Earth Engine (GEE)을 사용하는 실제 사례를 제공했습니다. 중요한 점은 SDM 분야에서 GEE의 다재다능함과 유연성입니다. Earth Engine의 강력한 지리 공간 데이터 처리 기능을 활용하면 연구자와 환경 보호론자가 지구의 생물 다양성을 이해하고 보존할 수 있는 무한한 가능성이 열립니다. 이 튜토리얼에서 얻은 지식과 기술을 적용하면 개인이 이 흥미로운 생태 연구 분야를 탐색하고 기여할 수 있습니다.
 Google Colab에서 실행
Google Colab에서 실행
 GitHub에서 소스 보기
GitHub에서 소스 보기