ประกาศ: โปรเจ็กต์ที่ไม่ใช่เชิงพาณิชย์ทั้งหมดที่ลงทะเบียนเพื่อใช้ Earth Engine ก่อนวันที่ 15 เมษายน 2025 ต้องยืนยันการมีสิทธิ์ที่ไม่ใช่เชิงพาณิชย์เพื่อรักษาสิทธิ์เข้าถึง Earth Engine

หน้านี้ได้รับการแปลโดย Cloud Translation API

การจำลองการกระจายพันธุ์ของสิ่งมีชีวิต

ผู้เขียน: osgeokr

เรียกใช้ใน Google Colab

ดูแหล่งที่มาใน GitHub

ในบทแนะนำนี้ เราจะแนะนำวิธีการสร้างแบบจำลองการกระจายพันธุ์โดยใช้ Google Earth Engine เราจะอธิบายภาพรวมโดยย่อของการสร้างแบบจำลองการกระจายพันธุ์ ตามด้วยกระบวนการคาดการณ์และวิเคราะห์ถิ่นที่อยู่ของนกที่ใกล้สูญพันธุ์ซึ่งรู้จักกันในชื่อนกพิตต้านางฟ้า (ชื่อวิทยาศาสตร์: Pitta nympha)

เรียกใช้ฉันก่อน

เรียกใช้เซลล์ต่อไปนี้เพื่อเริ่มต้น API เอาต์พุตจะมีวิธีการให้สิทธิ์เข้าถึง Earth Engine แก่ Notebook นี้โดยใช้บัญชีของคุณ

import ee

# Trigger the authentication flow.
ee.Authenticate()

# Initialize the library.
ee.Initialize(project='my-project')

ภาพรวมโดยย่อของการสร้างแบบจำลองการกระจายพันธุ์

มาดูกันว่าโมเดลการกระจายพันธุ์คืออะไร ข้อดีของการใช้ Google Earth Engine ในการประมวลผล ข้อมูลที่จำเป็นสำหรับโมเดล และโครงสร้างของเวิร์กโฟลว์

การสร้างแบบจำลองการกระจายพันธุ์คืออะไร

การสร้างแบบจำลองการกระจายพันธุ์ (SDM ด้านล่าง) เป็นวิธีการที่ใช้กันมากที่สุดในการประมาณการกระจายพันธุ์ตามภูมิศาสตร์ที่แท้จริงหรือที่อาจเกิดขึ้นของสายพันธุ์ ซึ่งเกี่ยวข้องกับการระบุลักษณะสภาพแวดล้อมที่เหมาะสมสำหรับสปีชีส์หนึ่งๆ แล้วระบุว่าสภาพแวดล้อมที่เหมาะสมเหล่านี้กระจายตัวอยู่ ณ ที่ใดในเชิงภูมิศาสตร์

SDM กลายเป็นองค์ประกอบสำคัญของการวางแผนการอนุรักษ์ในช่วงไม่กี่ปีที่ผ่านมา และมีการพัฒนาเทคนิคการสร้างโมเดลต่างๆ เพื่อจุดประสงค์นี้ การใช้ SDM ใน Google Earth Engine (GEE ด้านล่าง) ช่วยให้เข้าถึงข้อมูลด้านสิ่งแวดล้อมขนาดใหญ่ได้ง่าย พร้อมด้วยความสามารถในการประมวลผลที่มีประสิทธิภาพและการรองรับอัลกอริทึมแมชชีนเลิร์นนิง ซึ่งช่วยให้สร้างโมเดลได้อย่างรวดเร็ว

หมายเหตุ: นักชีววิทยาเชิงอนุรักษ์ ดร. รามิโร ดี. Crego ใช้ SDM โดยใช้โปรแกรมแก้ไขโค้ด JavaScript ของ GEE และเผยแพร่ผลการวิจัยของเขา (Crego et al, 2022) วิธีการของ SDM ที่แนะนำในที่นี้ได้รับการแปลและแก้ไขจากซอร์สโค้ด JavaScript ที่เขาแชร์เป็นภาษา Python

ข้อมูลที่จำเป็นสำหรับ SDM

โดยปกติแล้ว SDM จะใช้ความสัมพันธ์ระหว่างบันทึกการเกิดของสายพันธุ์ที่ทราบกับตัวแปรด้านสิ่งแวดล้อมเพื่อระบุเงื่อนไขที่ประชากรสามารถอยู่รอดได้ กล่าวโดยสรุปคือ คุณต้องระบุข้อมูลอินพุตของโมเดล 2 ประเภท ได้แก่

บันทึกการเกิดของสายพันธุ์ที่รู้จัก
ตัวแปรด้านสิ่งแวดล้อมต่างๆ

ระบบจะป้อนข้อมูลเหล่านี้ลงในอัลกอริทึมเพื่อระบุสภาพแวดล้อมที่เกี่ยวข้องกับการมีอยู่ของสายพันธุ์

เวิร์กโฟลว์ของ SDM โดยใช้ GEE

ขั้นตอนการทำงานสำหรับ SDM โดยใช้ GEE มีดังนี้

การเก็บรวบรวมและการประมวลผลล่วงหน้าของข้อมูลการเกิดของสายพันธุ์
คำจำกัดความของพื้นที่ที่สนใจ
การเพิ่มตัวแปรสภาพแวดล้อมของ GEE
การสร้างข้อมูลการขาดเรียนแบบจำลอง
การปรับโมเดลและการคาดการณ์
การประเมินความสําคัญและความแม่นยําของตัวแปร

การคาดการณ์และการวิเคราะห์ที่อยู่อาศัยโดยใช้ GEE

เราจะใช้นกพิตต้าเทวรูป (Pitta nympha) เป็นกรณีศึกษาเพื่อแสดงให้เห็นการประยุกต์ใช้ SDM ที่อิงตาม GEE แม้ว่าเราจะเลือกสายพันธุ์นี้มาเป็นตัวอย่างหนึ่ง แต่ในความเป็นจริงแล้ว นักวิจัยสามารถนำวิธีการนี้ไปใช้กับสายพันธุ์เป้าหมายที่สนใจได้โดยปรับเปลี่ยนซอร์สโค้ดที่ให้มาเล็กน้อย

นกพิตต้าเทวดาเป็นนกอพยพช่วงฤดูร้อนและนกอพยพผ่านที่พบได้ยากในเกาหลีใต้ ซึ่งมีพื้นที่กระจายพันธุ์เพิ่มขึ้นเนื่องจากคาบสมุทรเกาหลีมีอุณหภูมิสูงขึ้นในช่วงไม่กี่ปีที่ผ่านมา โดยจัดเป็นสายพันธุ์หายาก สัตว์ป่าที่ใกล้สูญพันธุ์ในชั้นที่ 2 อนุสรณ์สถานทางธรรมชาติหมายเลข 204 ประเมินว่าสูญพันธุ์ในระดับภูมิภาค (RE) ในบัญชีแดงแห่งชาติ และอยู่ในกลุ่มเสี่ยง (VU) ตามหมวดหมู่ของ IUCN

การทำ SDM เพื่อวางแผนการอนุรักษ์นกพิตต้าเทวดูเหมือนจะมีประโยชน์อย่างมาก ตอนนี้เรามาดูการคาดการณ์และการวิเคราะห์แหล่งที่อยู่อาศัยผ่าน GEE กัน

ขั้นแรกคือการนำเข้าไลบรารี Python โดยคำสั่ง import จะนำเข้าเนื้อหาทั้งหมดของโมดูล ในขณะที่คำสั่ง from import จะอนุญาตให้นำเข้าออบเจ็กต์ที่เฉพาะเจาะจงจากโมดูล

# Import libraries
import geemap

import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random

from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor

การรวบรวมและการประมวลผลล่วงหน้าของข้อมูลการเกิดของสายพันธุ์

ตอนนี้มาเก็บรวบรวมข้อมูลการเกิดของนกพิตต้าเทวา แม้ว่าปัจจุบันคุณจะไม่มีสิทธิ์เข้าถึงข้อมูลการเกิดของสายพันธุ์ที่สนใจ แต่ก็สามารถรับข้อมูลการสังเกตการณ์เกี่ยวกับสายพันธุ์ที่เฉพาะเจาะจงผ่าน GBIF API ได้ GBIF API เป็นอินเทอร์เฟซที่อนุญาตให้เข้าถึงข้อมูลการกระจายพันธุ์ที่ GBIF จัดหาให้ ซึ่งช่วยให้ผู้ใช้ค้นหา กรอง และดาวน์โหลดข้อมูล รวมถึงรับข้อมูลต่างๆ ที่เกี่ยวข้องกับสายพันธุ์ได้

ในโค้ดด้านล่าง ระบบจะกำหนดชื่อวิทยาศาสตร์ของสายพันธุ์ให้กับตัวแปร species_name (เช่น Pitta nympha สำหรับนกพิตต้าเทวรูป) และกำหนดรหัสประเทศให้กับตัวแปร country_code (เช่น KR สำหรับเกาหลีใต้) ตัวแปร base_url จะจัดเก็บที่อยู่ของ GBIF API params คือพจนานุกรมที่มีพารามิเตอร์ที่จะใช้ในคำขอ API

scientificName: ตั้งชื่อวิทยาศาสตร์ของสายพันธุ์ที่จะค้นหา
country: จำกัดการค้นหาให้แสดงเฉพาะในประเทศที่ระบุ
hasCoordinate: ตรวจสอบว่ามีการค้นหาเฉพาะข้อมูลที่มีพิกัด (จริง)
basisOfRecord: เลือกเฉพาะบันทึกการสังเกตของมนุษย์ (HUMAN_OBSERVATION)
limit: ตั้งค่าจำนวนผลลัพธ์สูงสุดที่แสดงเป็น 10000

def get_gbif_species_data(species_name, country_code):
    """
    Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.

    Parameters:
    species_name (str): The scientific name of the species to query.
    country_code (str): The country code of the where the observation data will be queried.

    Returns:
    pd.DataFrame: A pandas DataFrame containing the observational data.
    """
    base_url = "https://api.gbif.org/v1/occurrence/search"
    params = {
        "scientificName": species_name,
        "country": country_code,
        "hasCoordinate": "true",
        "basisOfRecord": "HUMAN_OBSERVATION",
        "limit": 10000,
    }

    try:
        response = requests.get(base_url, params=params)
        response.raise_for_status()  # Raises an exception for a response error.
        data = response.json()
        occurrences = data.get("results", [])

        if occurrences:  # If data is present
            df = pd.json_normalize(occurrences)
            return df
        else:
            print("No data found for the given species and country code.")
            return pd.DataFrame()  # Returns an empty DataFrame
    except requests.RequestException as e:
        print(f"Request failed: {e}")
        return pd.DataFrame()  # Returns an empty DataFrame in case of an exception

เราใช้พารามิเตอร์ที่ตั้งค่าไว้ก่อนหน้านี้เพื่อค้นหา API ของ GBIF สำหรับบันทึกการสังเกตของนกพิตต้าแฟรี (Pitta nympha) และโหลดผลลัพธ์ลงใน DataFrame เพื่อตรวจสอบแถวแรก DataFrame คือโครงสร้างข้อมูลสำหรับจัดการข้อมูลที่จัดรูปแบบตาราง ซึ่งประกอบด้วยแถวและคอลัมน์ หากจำเป็น คุณสามารถบันทึก DataFrame เป็นไฟล์ CSV และอ่านกลับได้

# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1)  # Display the first row of the DataFrame

จากนั้นเราจะแปลง DataFrame เป็น GeoDataFrame ซึ่งมีคอลัมน์สำหรับข้อมูลทางภูมิศาสตร์ (geometry) และตรวจสอบแถวแรก คุณบันทึก GeoDataFrame เป็นไฟล์ GeoPackage (*.gpkg) และอ่านกลับได้

# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
    df,
    geometry=gpd.points_from_xy(df.decimalLongitude,
                                df.decimalLatitude),
    crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1)  # Display the first row of the GeoDataFrame

ครั้งนี้เราได้สร้างฟังก์ชันเพื่อแสดงภาพการกระจายข้อมูลตามปีและเดือนจาก GeoDataFrame และแสดงเป็นกราฟ ซึ่งจะบันทึกเป็นไฟล์รูปภาพได้ การใช้แผนที่ความร้อนช่วยให้เราทราบความถี่ของการเกิดสายพันธุ์ตามปีและเดือนได้อย่างรวดเร็ว ซึ่งเป็นการแสดงภาพการเปลี่ยนแปลงและรูปแบบชั่วคราวภายในข้อมูลอย่างเป็นธรรมชาติ ซึ่งจะช่วยให้ระบุรูปแบบตามเวลาและความผันแปรตามฤดูกาลในข้อมูลการเกิดของสายพันธุ์ รวมถึงตรวจหาค่าผิดปกติหรือปัญหาด้านคุณภาพภายในข้อมูลได้อย่างรวดเร็ว

# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):

    statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)

    # Heatmap
    plt.figure(figsize=(h_size, h_size - 6))
    heatmap = plt.imshow(
        statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
    )

    # Display values above each pixel
    for i in range(len(statistics.index)):
        for j in range(len(statistics.columns)):
            plt.text(
                j, i, statistics.values[i, j], ha="center", va="center", color="black"
            )

    plt.colorbar(heatmap, label="Count")
    plt.title("Monthly Species Count by Year")
    plt.xlabel("Year")
    plt.ylabel("Month")
    plt.xticks(range(len(statistics.columns)), statistics.columns)
    plt.yticks(range(len(statistics.index)), statistics.index)
    plt.tight_layout()
    plt.savefig("heatmap_plot.png")
    plt.show()

plot_heatmap(gdf)

ข้อมูลตั้งแต่ปี 1995 มีอยู่น้อยมากและมีช่องว่างอย่างเห็นได้ชัดเมื่อเทียบกับปีอื่นๆ นอกจากนี้ เดือนสิงหาคมและกันยายนยังมีตัวอย่างจำกัดและแสดงลักษณะตามฤดูกาลที่แตกต่างจากช่วงอื่นๆ การยกเว้นข้อมูลนี้อาจช่วยปรับปรุงความเสถียรและความสามารถในการคาดการณ์ของโมเดล

อย่างไรก็ตาม โปรดทราบว่าการยกเว้นข้อมูลอาจช่วยเพิ่มความสามารถในการสรุปทั่วไปของโมเดล แต่ก็อาจทําให้สูญเสียข้อมูลที่มีค่าซึ่งเกี่ยวข้องกับวัตถุประสงค์ของการวิจัยได้เช่นกัน ดังนั้น การตัดสินใจดังกล่าวจึงควรพิจารณาอย่างรอบคอบ

# Filtering data by year and month
filtered_gdf = gdf[
    (~gdf['year'].eq(1995)) &
    (~gdf['month'].between(8, 9))
]

ตอนนี้ระบบจะแปลง GeoDataFrame ที่กรองแล้วเป็นออบเจ็กต์ Google Earth Engine

# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)

จากนั้นเราจะกำหนดขนาดพิกเซลของแรสเตอร์ของผลลัพธ์ SDM เป็นความละเอียด 1 กม.

# Spatial resolution setting (meters)
grain_size = 1000

เมื่อมีจุดเกิดหลายจุดภายในพิกเซลแรสเตอร์ที่มีความละเอียด 1 กม. มีแนวโน้มสูงที่จุดเหล่านั้นจะมีสภาพแวดล้อมเดียวกันในสถานที่ตั้งทางภูมิศาสตร์เดียวกัน การใช้ข้อมูลดังกล่าวในการวิเคราะห์โดยตรงอาจทำให้ผลลัพธ์เกิดอคติ

กล่าวคือ เราต้องจำกัดผลกระทบที่อาจเกิดขึ้นจากอคติในการสุ่มตัวอย่างตามภูมิศาสตร์ เราจึงจะเก็บเฉพาะตำแหน่งเดียวภายในพิกเซลแต่ละกิโลเมตรและนำตำแหน่งอื่นๆ ทั้งหมดออก เพื่อให้โมเดลแสดงสภาพแวดล้อมได้อย่างเป็นกลางมากขึ้น

def remove_duplicates(data, grain_size):
    # Select one occurrence record per pixel at the chosen spatial resolution
    random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
    rand_point_vals = random_raster.sampleRegions(
        collection=ee.FeatureCollection(data), geometries=True
    )
    return rand_point_vals.distinct("random")


data = remove_duplicates(data_raw, grain_size)

# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())

ภาพการเปรียบเทียบความเอนเอียงในการสุ่มตัวอย่างทางภูมิศาสตร์ก่อนการประมวลผลล่วงหน้า (สีน้ำเงิน) และหลังการประมวลผลล่วงหน้า (สีแดง) แสดงอยู่ด้านล่าง เพื่อช่วยในการเปรียบเทียบ เราจึงวางแผนที่ไว้ตรงกลางบริเวณที่มีพิกัดการเกิดของนกพิตต้าท้องขาวในอุทยานแห่งชาติฮัลลาซาน

# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
    random_raster,
    {"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
    "Random Raster",
)

# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")

# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")

# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map

คำจำกัดความของพื้นที่ที่สนใจ

การกำหนดพื้นที่ที่สนใจ (AOI ด้านล่าง) หมายถึงคำที่นักวิจัยใช้เพื่อระบุพื้นที่ทางภูมิศาสตร์ที่ต้องการวิเคราะห์ ซึ่งมีความหมายคล้ายกับคำว่าพื้นที่ศึกษา

ในบริบทนี้ เราได้กล่องขอบเขตของรูปเรขาคณิตของเลเยอร์จุดที่เกิดเหตุการณ์ และสร้างบัฟเฟอร์ 50 กิโลเมตรรอบๆ (โดยมีความคลาดเคลื่อนสูงสุด 1,000 เมตร) เพื่อกำหนด AOI

# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)

# Add the AOI to the map
outline = ee.Image().byte().paint(
    featureCollection=aoi, color=1, width=3)

Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map

การเพิ่มตัวแปรสภาพแวดล้อมของ GEE

ตอนนี้มาเพิ่มตัวแปรด้านสิ่งแวดล้อมลงในการวิเคราะห์กัน GEE มีชุดข้อมูลที่หลากหลายสำหรับตัวแปรด้านสิ่งแวดล้อม เช่น อุณหภูมิ ปริมาณน้ำฝน ความสูงเหนือระดับน้ำทะเล สิ่งปกคลุมดิน และภูมิประเทศ ชุดข้อมูลเหล่านี้ช่วยให้เราวิเคราะห์ปัจจัยต่างๆ ที่อาจส่งผลต่อความชอบในถิ่นที่อยู่ของนกพิตต้านางฟ้าได้อย่างครอบคลุม

การเลือกตัวแปรด้านสิ่งแวดล้อมของ GEE ใน SDM ควรแสดงลักษณะค่ากำหนดของที่อยู่อาศัยของสายพันธุ์ โดยต้องทำการวิจัยเบื้องต้นและทบทวนวรรณกรรมเกี่ยวกับความชอบในถิ่นที่อยู่ของนกพิตต้าเทวาก่อน บทแนะนำนี้มุ่งเน้นที่เวิร์กโฟลว์ของ SDM โดยใช้ GEE เป็นหลัก จึงอาจไม่มีรายละเอียดเชิงลึกบางอย่าง

WorldClim V1 Bioclim: ชุดข้อมูลนี้มีตัวแปรทางชีวภูมิอากาศ 19 รายการที่ได้มาจากข้อมูลอุณหภูมิและปริมาณน้ำฝนรายเดือน โดยครอบคลุมช่วงปี 1960-1991 และมีความละเอียด 927.67 เมตร

# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")

ความสูงแบบดิจิทัล 30 ม. ของ SRTM จาก NASA: ชุดข้อมูลนี้มีข้อมูลความสูงแบบดิจิทัลจากภารกิจ Shuttle Radar Topography Mission (SRTM) ข้อมูลนี้รวบรวมขึ้นในช่วงปี 2000 เป็นหลัก และมีความละเอียดประมาณ 30 เมตร (1 อาร์ควินาที) โค้ดต่อไปนี้จะคำนวณเลเยอร์ความสูง ความชัน ลักษณะ และการแรเงาภูมิประเทศจากข้อมูล SRTM

# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))

การเปลี่ยนแปลงของพื้นที่ปกคลุมป่าไม้ทั่วโลก (GFCC) พื้นที่ปกคลุมต้นไม้ทั่วโลกแบบหลายปีที่ 30 ม.: ชุดข้อมูลฟิลด์ต่อเนื่องของพืชพรรณ (VCF) จาก Landsat จะประมาณสัดส่วนของพื้นที่ปกคลุมพืชพรรณที่ฉายในแนวตั้งเมื่อความสูงของพืชพรรณมากกว่า 5 เมตร ชุดข้อมูลนี้มีให้สำหรับช่วงเวลา 4 ช่วงโดยมีศูนย์กลางอยู่ที่ปี 2000, 2005, 2010 และ 2015 โดยมีความละเอียด 30 เมตร ในที่นี้ เราใช้ค่ามัธยฐานจากระยะเวลา 4 ช่วงนี้

# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
    tcc.filterDate("2000-01-01", "2015-12-31")
    .select(["tree_canopy_cover"], ["TCC"])
    .median()
)

bio (ตัวแปรทางชีวภูมิอากาศ) terrain (ภูมิประเทศ) และ median_tcc (พื้นที่ปกคลุมของเรือนยอดไม้) จะรวมกันเป็นรูปภาพหลายแถบความถี่เดียว ระบบจะเลือกแถบ elevation จาก terrain และสร้าง watermask สำหรับสถานที่ที่ elevation มากกว่า 0 ซึ่งจะปิดบังภูมิภาคที่อยู่ต่ำกว่าระดับน้ำทะเล (เช่น มหาสมุทร) และเตรียมให้นักวิจัยวิเคราะห์ปัจจัยด้านสิ่งแวดล้อมต่างๆ สำหรับ AOI อย่างครอบคลุม

# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)

# Create a water mask
watermask = terrain.select('elevation').gt(0)

# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)

เมื่อรวมตัวแปรทำนายที่มีความสัมพันธ์สูงไว้ด้วยกันในโมเดล อาจเกิดปัญหาความสัมพันธ์เชิงเส้นพหุ Multicollinearity เป็นปรากฏการณ์ที่เกิดขึ้นเมื่อมีความสัมพันธ์เชิงเส้นที่แข็งแกร่งระหว่างตัวแปรอิสระในโมเดล ซึ่งทําให้การประมาณค่าสัมประสิทธิ์ (น้ำหนัก) ของโมเดลไม่เสถียร ความไม่เสถียรนี้อาจลดความน่าเชื่อถือของโมเดลและทำให้การคาดการณ์หรือการตีความข้อมูลใหม่เป็นเรื่องยาก ดังนั้นเราจะพิจารณาความสัมพันธ์เชิงเส้นพหุและดำเนินการตามกระบวนการเลือกตัวแปรทำนาย

ก่อนอื่น เราจะสร้างจุดแบบสุ่ม 5,000 จุด แล้วดึงค่าตัวแปรทำนายของรูปภาพหลายแถบความถี่เดี่ยวที่จุดเหล่านั้น

# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)

# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)

เราจะแปลงค่าตัวทำนายที่ดึงออกมาสำหรับแต่ละจุดเป็น DataFrame แล้วตรวจสอบแถวแรก

# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)

# Displaying the columns
columns = pvals_df.columns
print(columns)

การคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของ Spearman ระหว่างตัวแปรทำนายที่กำหนดและการแสดงภาพในฮีตแมป

def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
    # Calculate Spearman correlation coefficients
    correlation_matrix = dataframe.corr(method="spearman")

    # Create a heatmap
    plt.figure(figsize=(h_size, h_size-2))
    plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')

    # Optionally display values on the heatmap
    if show_labels:
        for i in range(correlation_matrix.shape[0]):
            for j in range(correlation_matrix.shape[1]):
                plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
                         ha='center', va='center', color='white', fontsize=8)

    columns = dataframe.columns.tolist()
    plt.xticks(range(len(columns)), columns, rotation=90)
    plt.yticks(range(len(columns)), columns)
    plt.title("Variables Correlation Matrix")
    plt.colorbar(label="Spearman Correlation")
    plt.savefig('correlation_heatmap_plot.png')
    plt.show()

# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)

สัมประสิทธิ์สหสัมพันธ์ของ Spearman มีประโยชน์ในการทำความเข้าใจความสัมพันธ์ทั่วไประหว่างตัวแปรทำนาย แต่ไม่ได้ประเมินโดยตรงว่าตัวแปรหลายตัวโต้ตอบกันอย่างไร โดยเฉพาะการตรวจหาภาวะหลายเส้น

ค่าความแปรปรวนที่เพิ่มขึ้น (VIF ด้านล่าง) คือเมตริกทางสถิติที่ใช้ในการประเมินความสัมพันธ์เชิงเส้นพหุคูณและแนะนําการเลือกตัวแปร ซึ่งจะบ่งบอกถึงระดับความสัมพันธ์เชิงเส้นของตัวแปรอิสระแต่ละตัวกับตัวแปรอิสระอื่นๆ และค่า VIF สูงอาจเป็นหลักฐานของ Multicollinearity

โดยปกติแล้ว เมื่อค่า VIF เกิน 5 หรือ 10 แสดงว่าตัวแปรมีความสัมพันธ์อย่างมากกับตัวแปรอื่นๆ ซึ่งอาจส่งผลต่อความเสถียรและความสามารถในการตีความของโมเดล ในบทแนะนำนี้ มีการใช้เกณฑ์ค่า VIF น้อยกว่า 10 สำหรับการเลือกตัวแปร ระบบเลือกตัวแปร 6 รายการต่อไปนี้ตาม VIF

# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):

    original_columns = dataframe.columns.tolist()
    remaining_columns = original_columns[:]

    while True:
        vif_data = dataframe[remaining_columns]
        vif_values = [
            variance_inflation_factor(vif_data.values, i)
            for i in range(vif_data.shape[1])
        ]

        max_vif_index = vif_values.index(max(vif_values))
        max_vif = max(vif_values)

        if max_vif < threshold:
            break

        print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")

        del remaining_columns[max_vif_index]

    filtered_data = dataframe[remaining_columns]
    bands = filtered_data.columns.tolist()
    print("Bands:", bands)

    return filtered_data, bands

filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)

# Variable Selection Based on VIF
predictors = predictors.select(bands)

# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)

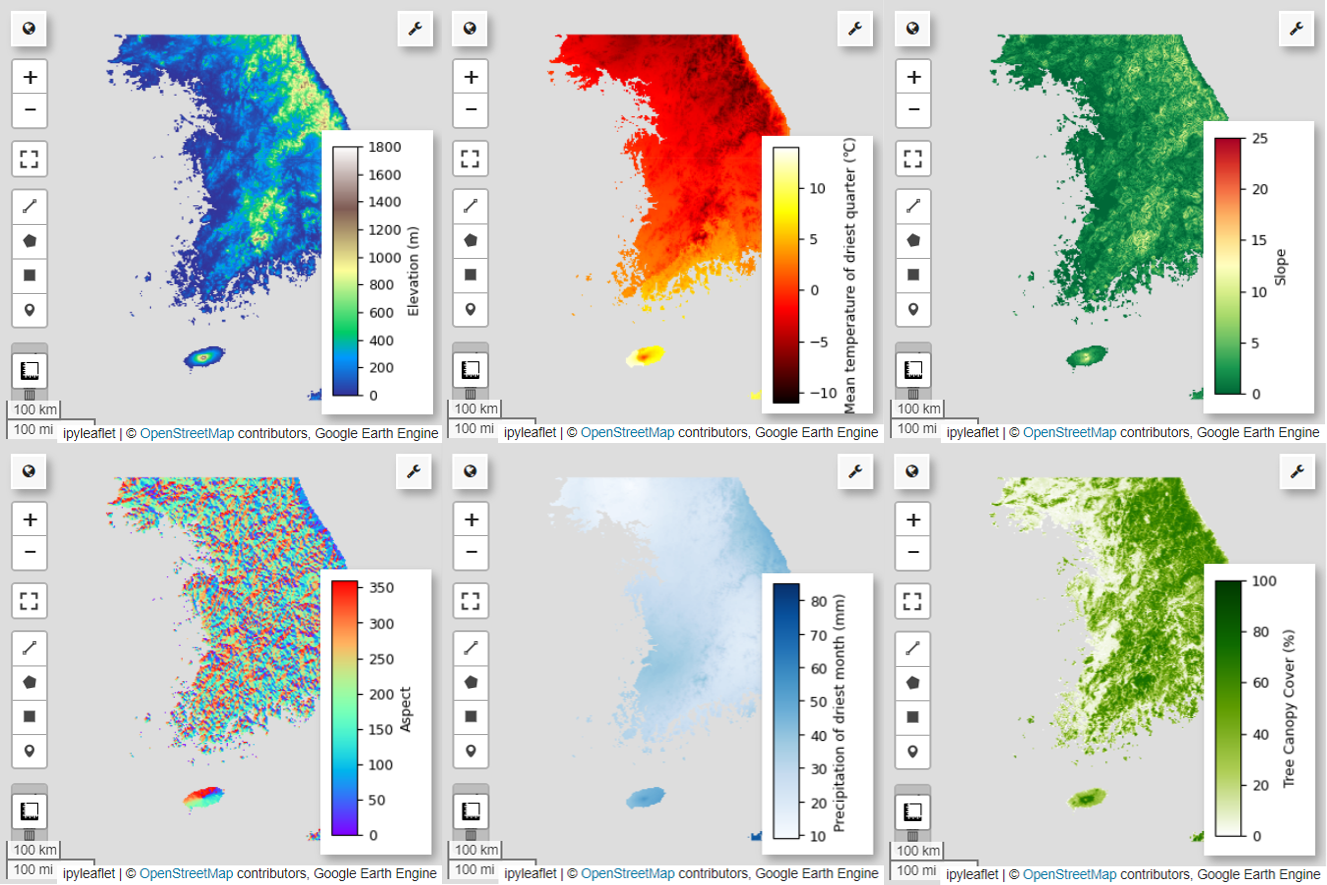
จากนั้นมาแสดงภาพตัวแปรทำนายที่เลือก 6 รายการบนแผนที่กัน ตัวแปรทำนายสำหรับการวิเคราะห์

คุณสำรวจจานสีที่ใช้ได้สำหรับการแสดงภาพแผนที่ได้โดยใช้โค้ดต่อไปนี้ เช่น จานสี terrain จะมีลักษณะดังนี้ cm.plot_colormaps(width=8.0, height=0.2)

cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')

# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map

# Calculate the minimum and maximum values for bio09
min_max_val = (
    predictors.select("bio09")
    .multiply(0.1)
    .reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
    .getInfo()
)

# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "min": math.floor(min_max_val["bio09_min"]),
    "max": math.ceil(min_max_val["bio09_max"]),
    "palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
    vis_params,
    label="Mean temperature of driest quarter (℃)",
    orientation="vertical",
    layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map

# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map

# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})

vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map

# Calculate the minimum and maximum values for bio14
min_max_val = (
    predictors.select("bio14")
    .reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
    .getInfo()
)

# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "bands": ["bio14"],
    "min": math.floor(min_max_val["bio14_min"]),
    "max": math.ceil(min_max_val["bio14_max"]),
    "palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
    vis_params,
    label="Precipitation of driest month (mm)",
    orientation="vertical",
    layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map

# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})

vis_params = {
    "bands": ["TCC"],
    "min": 0,
    "max": 100,
    "palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
    vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map

การสร้างข้อมูลการขาดเรียนแบบจำลอง

ในกระบวนการ SDM การเลือกข้อมูลอินพุตสำหรับสปีชีส์จะดำเนินการโดยใช้วิธีการหลัก 2 วิธี ดังนี้

วิธีใช้ข้อมูลการพบเห็นเป็นพื้นฐาน: วิธีนี้จะเปรียบเทียบสถานที่ที่พบเห็นสายพันธุ์หนึ่งๆ (การพบเห็น) กับสถานที่อื่นๆ ที่ไม่พบเห็นสายพันธุ์นั้น (พื้นฐาน) ในที่นี้ ข้อมูลพื้นหลังไม่ได้หมายถึงพื้นที่ที่ไม่มีสายพันธุ์นั้นๆ แต่เป็นการตั้งค่าเพื่อแสดงถึงสภาพแวดล้อมโดยรวมของพื้นที่ศึกษา โดยใช้เพื่อแยกแยะสภาพแวดล้อมที่เหมาะสมซึ่งอาจมีสายพันธุ์อยู่จากสภาพแวดล้อมที่เหมาะสมน้อยกว่า
วิธีดูว่ามีหรือไม่มี: วิธีนี้จะเปรียบเทียบสถานที่ที่พบสายพันธุ์ (มี) กับสถานที่ที่ไม่พบสายพันธุ์ (ไม่มี) ในที่นี้ ข้อมูลการไม่อยู่แสดงถึงสถานที่ที่เฉพาะเจาะจงซึ่งทราบว่าไม่มีสายพันธุ์นั้นอยู่ โดยไม่ได้แสดงถึงสภาพแวดล้อมโดยรวมของพื้นที่ศึกษา แต่ชี้ไปยังสถานที่ที่คาดว่าไม่มีสายพันธุ์

ในทางปฏิบัติ การเก็บรวบรวมข้อมูลการไม่อยู่จริงมักเป็นเรื่องยาก จึงมักใช้ข้อมูลการไม่อยู่เทียมที่สร้างขึ้น อย่างไรก็ตาม สิ่งสำคัญคือต้องรับทราบข้อจำกัดและข้อผิดพลาดที่อาจเกิดขึ้นของวิธีนี้ เนื่องจากจุดที่ไม่มีอยู่จริงซึ่งสร้างขึ้นโดยอัตโนมัติอาจไม่สะท้อนถึงพื้นที่ที่ไม่มีอยู่จริงอย่างถูกต้อง

การเลือกระหว่าง 2 วิธีนี้ขึ้นอยู่กับความพร้อมใช้งานของข้อมูล วัตถุประสงค์ของการวิจัย ความแม่นยำและความน่าเชื่อถือของโมเดล รวมถึงเวลาและทรัพยากร ในที่นี้ เราจะใช้ข้อมูลการเกิดที่รวบรวมจาก GBIF และข้อมูลการไม่อยู่เทียมที่สร้างขึ้นเพื่อจำลองโดยใช้วิธี "การมีอยู่-การไม่อยู่"

การสร้างข้อมูลการไม่อยู่เทียมจะดำเนินการผ่าน "แนวทางการสร้างโปรไฟล์สภาพแวดล้อม" โดยมีขั้นตอนเฉพาะดังนี้

การจัดประเภทสภาพแวดล้อมโดยใช้การจัดกลุ่ม k-means: เราจะใช้อัลกอริทึมการจัดกลุ่ม k-means ตามระยะทางแบบยุคลิดเพื่อแบ่งพิกเซลภายในพื้นที่ศึกษาออกเป็น 2 คลัสเตอร์ คลัสเตอร์หนึ่งจะแสดงพื้นที่ที่มีลักษณะด้านสิ่งแวดล้อมคล้ายกับสถานที่ตั้ง 100 แห่งที่เลือกแบบสุ่ม ส่วนอีกคลัสเตอร์จะแสดงพื้นที่ที่มีลักษณะแตกต่างกัน
การสร้างข้อมูลการไม่อยู่เสมือนภายในคลัสเตอร์ที่ไม่คล้ายกัน: ภายในคลัสเตอร์ที่ 2 ที่ระบุในขั้นตอนแรก (ซึ่งมีลักษณะด้านสิ่งแวดล้อมแตกต่างจากข้อมูลการอยู่) จะมีการสร้างจุดการไม่อยู่เสมือนที่สร้างขึ้นแบบสุ่ม จุดที่ไม่มีข้อมูลเหล่านี้จะแสดงตำแหน่งที่คาดว่าไม่มีสายพันธุ์

# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
    collection=data.randomColumn().sort('random').limit(100),
    properties=[],
    scale=grain_size
)

# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
    nClusters=2,
    distanceFunction="Euclidean"
).train(pvals)

cl_result = predictors.cluster(clusterer)

# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
    collection=data.randomColumn().sort('random').limit(200),
    properties=[],
    scale=grain_size
)

# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)

# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
            grain_size).mask().neq(1).selfMask()

# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)

# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map

การปรับโมเดลและการคาดการณ์

ตอนนี้เราจะแบ่งข้อมูลออกเป็นข้อมูลการฝึกและข้อมูลการทดสอบ ระบบจะใช้ข้อมูลการฝึกเพื่อค้นหาพารามิเตอร์ที่เหมาะสมที่สุดโดยการฝึกโมเดล ในขณะที่จะใช้ข้อมูลการทดสอบเพื่อประเมินโมเดลที่ฝึกไว้ก่อนหน้านี้ แนวคิดที่สำคัญที่ควรพิจารณาในบริบทนี้คือความสัมพันธ์ระหว่างค่าความคลาดเคลื่อนเชิงพื้นที่

การหาความสัมพันธ์เชิงพื้นที่เป็นองค์ประกอบสำคัญใน SDM ซึ่งเชื่อมโยงกับกฎของโทเบลอร์ โดยมีแนวคิดว่า "ทุกสิ่งทุกอย่างมีความสัมพันธ์กัน แต่สิ่งที่อยู่ใกล้กันจะมีความสัมพันธ์กันมากกว่าสิ่งที่อยู่ไกลกัน" การสหสัมพันธ์เชิงพื้นที่แสดงถึงความสัมพันธ์ที่สำคัญระหว่างตำแหน่งของสายพันธุ์และตัวแปรด้านสิ่งแวดล้อม อย่างไรก็ตาม หากมีความสัมพันธ์เชิงพื้นที่ระหว่างข้อมูลการฝึกและข้อมูลการทดสอบ ความเป็นอิสระระหว่างชุดข้อมูลทั้ง 2 ชุดอาจถูกบุกรุกได้ ซึ่งส่งผลต่อการประเมินความสามารถในการสรุปทั่วไปของโมเดลอย่างมาก

วิธีหนึ่งในการแก้ไขปัญหานี้คือเทคนิคการตรวจสอบความถูกต้องแบบไขว้เชิงพื้นที่ ซึ่งเกี่ยวข้องกับการแบ่งข้อมูลออกเป็นชุดข้อมูลการฝึกและการทดสอบ เทคนิคนี้เกี่ยวข้องกับการแบ่งข้อมูลออกเป็นหลายบล็อก โดยใช้แต่ละบล็อกอย่างอิสระเป็นชุดข้อมูลการฝึกและชุดข้อมูลการทดสอบเพื่อลดผลกระทบของการเชื่อมโยงเชิงพื้นที่ ซึ่งจะช่วยเพิ่มความเป็นอิสระระหว่างชุดข้อมูล ทำให้ประเมินความสามารถในการสรุปทั่วไปของโมเดลได้แม่นยำยิ่งขึ้น

ขั้นตอนที่เฉพาะเจาะจงมีดังนี้

การสร้างบล็อกเชิงพื้นที่: แบ่งชุดข้อมูลทั้งหมดออกเป็นบล็อกเชิงพื้นที่ที่มีขนาดเท่ากัน (เช่น 50x50 กม.)
การกำหนดชุดการฝึกและการทดสอบ: ระบบจะสุ่มกำหนดบล็อกเชิงพื้นที่แต่ละบล็อกให้กับชุดการฝึก (70%) หรือชุดทดสอบ (30%) ซึ่งจะช่วยป้องกันไม่ให้โมเดลปรับให้เหมาะกับข้อมูลจากบางพื้นที่มากเกินไป และมุ่งหวังที่จะให้ผลลัพธ์ที่ครอบคลุมมากขึ้น
การตรวจสอบแบบไขว้ซ้ำ: กระบวนการทั้งหมดจะทำซ้ำ n ครั้ง (เช่น 10 ครั้ง) ในแต่ละการทำซ้ำ ระบบจะแบ่งบล็อกแบบสุ่มออกเป็นชุดการฝึกและการทดสอบอีกครั้ง ซึ่งมีจุดประสงค์เพื่อปรับปรุงความเสถียรและความน่าเชื่อถือของโมเดล
การสร้างข้อมูลการไม่อยู่เทียม: ในแต่ละการทำซ้ำ ระบบจะสร้างข้อมูลการไม่อยู่เทียมแบบสุ่มเพื่อประเมินประสิทธิภาพของโมเดล

Scale = 50000
grid = watermask.reduceRegions(
    collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
    reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))

Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map

ตอนนี้เราสามารถปรับโมเดลได้แล้ว การปรับโมเดลเกี่ยวข้องกับการทำความเข้าใจรูปแบบในข้อมูลและการปรับพารามิเตอร์ของโมเดล (น้ำหนักและความเอนเอียง) ตามนั้น กระบวนการนี้ช่วยให้โมเดลคาดการณ์ได้แม่นยำมากขึ้นเมื่อได้รับข้อมูลใหม่ ด้วยเหตุนี้ เราจึงกำหนดฟังก์ชันที่ชื่อ SDM() เพื่อให้เหมาะกับโมเดล

เราจะใช้อัลกอริทึม Random Forest

def sdm(x):
    seed = ee.Number(x)

    # Random block division for training and validation
    rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
    training_grid = rand_blk.filter(ee.Filter.lt("random", split))  # Grid for training
    testing_grid = rand_blk.filter(ee.Filter.gte("random", split))  # Grid for testing

    # Presence points
    presence_points = ee.FeatureCollection(data)
    presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
    tr_presence_points = presence_points.filter(
        ee.Filter.bounds(training_grid)
    )  # Presence points for training
    te_presence_points = presence_points.filter(
        ee.Filter.bounds(testing_grid)
    )  # Presence points for testing

    # Pseudo-absence points for training
    tr_pseudo_abs_points = area_for_pa.sample(
        region=training_grid,
        scale=grain_size,
        numPixels=tr_presence_points.size().add(300),
        seed=seed,
        geometries=True,
    )
    # Same number of pseudo-absence points as presence points for training
    tr_pseudo_abs_points = (
        tr_pseudo_abs_points.randomColumn()
        .sort("random")
        .limit(ee.Number(tr_presence_points.size()))
    )
    tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))

    te_pseudo_abs_points = area_for_pa.sample(
        region=testing_grid,
        scale=grain_size,
        numPixels=te_presence_points.size().add(100),
        seed=seed,
        geometries=True,
    )
    # Same number of pseudo-absence points as presence points for testing
    te_pseudo_abs_points = (
        te_pseudo_abs_points.randomColumn()
        .sort("random")
        .limit(ee.Number(te_presence_points.size()))
    )
    te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))

    # Merge training and pseudo-absence points
    training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
    testing_partition = te_presence_points.merge(te_pseudo_abs_points)

    # Extract predictor variable values at training points
    train_pvals = predictors.sampleRegions(
        collection=training_partition,
        properties=["PresAbs"],
        scale=grain_size,
        geometries=True,
    )

    # Random Forest classifier
    classifier = ee.Classifier.smileRandomForest(
        numberOfTrees=500,
        variablesPerSplit=None,
        minLeafPopulation=10,
        bagFraction=0.5,
        maxNodes=None,
        seed=seed,
    )
    # Presence probability: Habitat suitability map
    classifier_pr = classifier.setOutputMode("PROBABILITY").train(
        train_pvals, "PresAbs", bands
    )
    classified_img_pr = predictors.select(bands).classify(classifier_pr)

    # Binary presence/absence map: Potential distribution map
    classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
        train_pvals, "PresAbs", bands
    )
    classified_img_bin = predictors.select(bands).classify(classifier_bin)

    return [
        classified_img_pr,
        classified_img_bin,
        training_partition,
        testing_partition,
    ], classifier_pr

บล็อกเชิงพื้นที่จะแบ่งออกเป็น 70% สำหรับการฝึกโมเดลและ 30% สำหรับการทดสอบโมเดลตามลำดับ ระบบจะสร้างข้อมูลการไม่อยู่เสมือนแบบสุ่มภายในชุดการฝึกและการทดสอบแต่ละชุดในทุกการทำซ้ำ ด้วยเหตุนี้ การดำเนินการแต่ละครั้งจึงให้ชุดข้อมูลการแสดงตนและข้อมูลการไม่แสดงตนแบบจำลองที่แตกต่างกันสำหรับการฝึกและทดสอบโมเดล

split = 0.7
numiter = 10

# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)

# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]

results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list

for item in items:
    result, trained = sdm(item)
    # Accumulate SDM results into the list
    results_list.extend(result)

    # Accumulate variable importance into the list
    importance = ee.Dictionary(trained.explain()).get('importance')
    importances_list.extend(importance.getInfo().items())

# Flatten the SDM results list
results = ee.List(results_list).flatten()

ตอนนี้เราสามารถแสดงภาพแผนที่ความเหมาะสมของถิ่นที่อยู่และแผนที่การกระจายพันธุ์ที่เป็นไปได้ของนกพิตต้าเทวาได้แล้ว ในกรณีนี้ ระบบจะสร้างแผนที่ความเหมาะสมของถิ่นที่อยู่โดยใช้ฟังก์ชัน mean() เพื่อคำนวณค่าเฉลี่ยสำหรับตำแหน่งพิกเซลแต่ละตำแหน่งในรูปภาพทั้งหมด และสร้างแผนที่การกระจายที่อาจเกิดขึ้นโดยใช้ฟังก์ชัน mode() เพื่อกำหนดค่าที่เกิดขึ้นบ่อยที่สุดในตำแหน่งพิกเซลแต่ละตำแหน่งในรูปภาพทั้งหมด

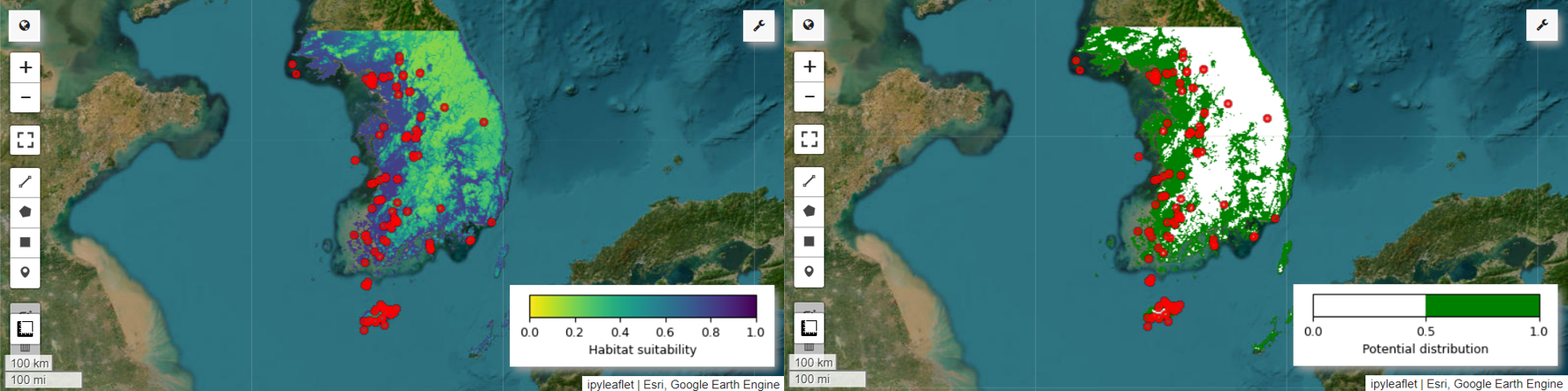
ผลลัพธ์ SDM

# Habitat suitability map
images = ee.List.sequence(
    0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
    lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()

Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')

vis_params = {
    'min': 0,
    'max': 1,
    'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
                 orientation="horizontal",
                 layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map

# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
    lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()

Map = geemap.Map(
    layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)

vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
    vis_params,
    label="Potential distribution",
    discrete=True,
    orientation="horizontal",
    layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map

การประเมินความสําคัญและความแม่นยําของตัวแปร

Random Forest (ee.Classifier.smileRandomForest) เป็นหนึ่งในวิธีการเรียนรู้แบบรวมกลุ่ม ซึ่งทำงานโดยสร้างต้นไม้ตัดสินใจหลายต้นเพื่อทำการคาดการณ์ ต้นไม้ตัดสินใจแต่ละต้นจะเรียนรู้จากชุดย่อยของข้อมูลที่แตกต่างกันโดยอิสระ และระบบจะรวบรวมผลลัพธ์เพื่อให้คาดการณ์ได้แม่นยำและเสถียรมากขึ้น

ความสําคัญของตัวแปรคือเมตริกที่ประเมินผลกระทบของตัวแปรแต่ละตัวต่อการคาดการณ์ภายในโมเดล Random Forest เราจะใช้ importances_list ที่กำหนดไว้ก่อนหน้านี้เพื่อคำนวณและพิมพ์ความสำคัญของตัวแปรเฉลี่ย

def plot_variable_importance(importances_list):
    # Extract each variable importance value into a list
    variables = [item[0] for item in importances_list]
    importances = [item[1] for item in importances_list]

    # Calculate the average importance for each variable
    average_importances = {}
    for variable in set(variables):
        indices = [i for i, var in enumerate(variables) if var == variable]
        average_importance = np.mean([importances[i] for i in indices])
        average_importances[variable] = average_importance

    # Sort the importances in descending order of importance
    sorted_importances = sorted(average_importances.items(),
                                key=lambda x: x[1], reverse=False)
    variables = [item[0] for item in sorted_importances]
    avg_importances = [item[1] for item in sorted_importances]

    # Adjust the graph size
    plt.figure(figsize=(8, 4))

    # Plot the average importance as a horizontal bar chart
    plt.barh(variables, avg_importances)
    plt.xlabel('Importance')
    plt.ylabel('Variables')
    plt.title('Average Variable Importance')

    # Display values above the bars
    for i, v in enumerate(avg_importances):
        plt.text(v + 0.02, i, f"{v:.2f}", va='center')

    # Adjust the x-axis range
    plt.xlim(0, max(avg_importances) + 5)  # Adjust to the desired range

    plt.tight_layout()
    plt.savefig('variable_importance.png')
    plt.show()

plot_variable_importance(importances_list)

เราใช้ชุดข้อมูลการทดสอบเพื่อคำนวณ AUC-ROC และ AUC-PR สำหรับการเรียกใช้แต่ละครั้ง จากนั้นเราจะคำนวณ AUC-ROC และ AUC-PR โดยเฉลี่ยในการทำซ้ำ n ครั้ง

AUC-ROC แสดงพื้นที่ใต้กราฟ "ความไว (การเรียกคืน) เทียบกับ 1-ความจำเพาะ" ซึ่งแสดงให้เห็นถึงความสัมพันธ์ระหว่างความไวและความจำเพาะเมื่อเกณฑ์เปลี่ยนแปลง ความจำเพาะจะอิงตามเหตุการณ์ทั้งหมดที่สังเกตได้ว่าไม่ได้เกิดขึ้น ดังนั้น AUC-ROC จึงครอบคลุมทั้ง 4 ส่วนของเมทริกซ์ความสับสน

AUC-PR แสดงพื้นที่ใต้กราฟ "ความแม่นยำเทียบกับความอ่อนไหว (ความไว)" ซึ่งแสดงความสัมพันธ์ระหว่างความแม่นยำกับความอ่อนไหวเมื่อเกณฑ์แตกต่างกัน ความแม่นยำอิงตามเหตุการณ์ที่คาดการณ์ทั้งหมด ดังนั้น AUC-PR จึงไม่รวมผลลบจริง (TN)

หมายเหตุ: คุณต้องตรวจสอบว่าการทดสอบแต่ละครั้งมีคะแนนเพียงพอสำหรับการตรวจสอบโมเดล จำนวนแต้มสุดท้ายอาจแตกต่างกันเนื่องจากการแบ่งพาร์ติชันแบบสุ่มของบล็อกเชิงพื้นที่ ดังนั้นจึงจำเป็นอย่างยิ่งที่จะต้องตรวจสอบว่ามีแต้มการปรากฏตัวและแต้มการไม่อยู่เทียมเพียงพอสำหรับการตรวจสอบโมเดลหรือไม่ ในกรณีของสายพันธุ์ที่ใกล้สูญพันธุ์หรือหายาก อาจมีข้อมูลการเกิดไม่เพียงพอ ซึ่งนำไปสู่ชุดข้อมูลทดสอบที่ไม่เพียงพอ ในกรณีดังกล่าว ทางเลือกอาจรวมถึงการเก็บรวบรวมข้อมูลเพิ่มเติมโดยอิงตามความรู้และประสบการณ์ของผู้เชี่ยวชาญ หรือการใช้แหล่งข้อมูลทางเลือกที่เกี่ยวข้อง

def print_pres_abs_sizes(TestingDatasets, numiter):
    # Check and print the sizes of presence and pseudo-absence coordinates
    def get_pres_abs_size(x):
        fc = ee.FeatureCollection(TestingDatasets.get(x))
        presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
        pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
        return ee.List([presence_size, pseudo_absence_size])

    sizes_info = (
        ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
        .map(get_pres_abs_size)
        .getInfo()
    )

    for i, sizes in enumerate(sizes_info):
        presence_size = sizes[0]
        pseudo_absence_size = sizes[1]
        print(
            f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
        )

# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
    3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))

print_pres_abs_sizes(testing_datasets, numiter)

def get_acc(hsm, t_data, grain_size):
    pr_prob_vals = hsm.sampleRegions(
        collection=t_data, properties=["PresAbs"], scale=grain_size
    )
    seq = ee.List.sequence(start=0, end=1, count=25)  # Divide 0 to 1 into 25 intervals

    def calculate_metrics(cutoff):
        # Each element of the seq list is passed as cutoff(threshold value)

        # Observed present = TP + FN
        pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)

        # TP (True Positive)
        tp = ee.Number(
            pres.filterMetadata("classification", "greater_than", cutoff).size()
        )

        # TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
        tpr = tp.divide(pres.size())

        # Observed absent = FP + TN
        abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)

        # FN (False Negative)
        fn = ee.Number(
            pres.filterMetadata("classification", "less_than", cutoff).size()
        )

        # TNR (True Negative Rate) = Specificity = TN  / (FP + TN) = TN / Observed absent
        tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
        tnr = tn.divide(abs.size())

        # FP (False Positive)
        fp = ee.Number(
            abs.filterMetadata("classification", "greater_than", cutoff).size()
        )

        # FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
        fpr = fp.divide(abs.size())

        # Precision = TP / (TP + FP) = TP / Predicted present
        precision = tp.divide(tp.add(fp))

        # SUMSS = SUM of Sensitivity and Specificity
        sumss = tpr.add(tnr)

        return ee.Feature(
            None,
            {
                "cutoff": cutoff,
                "TP": tp,
                "TN": tn,
                "FP": fp,
                "FN": fn,
                "TPR": tpr,
                "TNR": tnr,
                "FPR": fpr,
                "Precision": precision,
                "SUMSS": sumss,
            },
        )

    return ee.FeatureCollection(seq.map(calculate_metrics))

def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
    # Calculate AUC-ROC and AUC-PR
    def calculate_auc_metrics(x):
        hsm = ee.Image(images.get(x))
        t_data = ee.FeatureCollection(testing_datasets.get(x))
        acc = get_acc(hsm, t_data, grain_size)

        # Calculate AUC-ROC
        x = ee.Array(acc.aggregate_array("FPR"))
        y = ee.Array(acc.aggregate_array("TPR"))
        x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
        y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
        auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)

        # Calculate AUC-PR
        x = ee.Array(acc.aggregate_array("TPR"))
        y = ee.Array(acc.aggregate_array("Precision"))
        x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
        y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
        auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)

        return (auc_roc, auc_pr)

    auc_metrics = (
        ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
        .map(calculate_auc_metrics)
        .getInfo()
    )

    # Print AUC-ROC and AUC-PR for each iteration
    df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
    df.index = [f"Iteration {i + 1}" for i in range(len(df))]
    df.to_csv("auc_metrics.csv", index_label="Iteration")
    print(df)

    # Calculate mean and standard deviation of AUC-ROC and AUC-PR
    mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
    mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
    print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
    print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")

%%time

# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)

บทแนะนำนี้ได้แสดงตัวอย่างการใช้ Google Earth Engine (GEE) ในการสร้างแบบจำลองการกระจายพันธุ์ (SDM) ที่นำไปใช้ได้จริง ข้อควรทราบที่สำคัญคือความสามารถรอบด้านและความยืดหยุ่นของ GEE ในสาขา SDM การใช้ประโยชน์จากความสามารถในการประมวลผลข้อมูลเชิงพื้นที่อันทรงพลังของ Earth Engine จะเปิดโอกาสมากมายให้นักวิจัยและนักอนุรักษ์ได้ทำความเข้าใจและอนุรักษ์ความหลากหลายทางชีวภาพบนโลกของเรา การนำความรู้และทักษะที่ได้รับจากบทแนะนำนี้ไปใช้จะช่วยให้บุคคลต่างๆ ได้สำรวจและมีส่วนร่วมในสาขาการวิจัยด้านนิเวศวิทยาที่น่าสนใจนี้