移動先:
- コントロール変数の概要
- コントロール変数の選択
- コントロール係数の事前分布および事後分布のサンプルを抽出する
- 検索ボリュームをコントロール変数として含める
- 遅延変数を使用する
- 人口のスケーリング コントロール変数
- 対照群に因果推論とベースラインの分解がない理由
コントロール変数の概要
コントロール変数は、モデル内の変数のうち介入群変数でないものです。コントロール変数はベースラインの結果の推定に使用されます。ベースラインの結果とは、各介入群変数がすべての地域と期間のベースライン値に設定されているという反事実的シナリオにおいて、発生が想定される結果のことです(ベースライン値は、メディア変数の場合は常に 0 に割り当てられますが、メディア以外の介入群の場合は 0 以外が多くなります)。コントロール変数を使用すると、ベースラインの結果の推定と、介入群変数が結果に及ぼす因果効果の推定の精度が向上します。
コントロール変数は次のように分類できます。
交絡変数: 介入群と KPI に因果関係がある変数。交絡変数を含めることで、KPI に対する介入群の因果推定におけるバイアスを除外できます。
予測変数: KPI に因果関係があるものの、それ以外には影響しない変数。予測変数を含めても、介入群の因果効果のバイアスは除外されません。ただし、重要な予測指標を使用すると、因果推定値の分散を低減できます。
もう一つの変数タイプとして、メディエーター変数があります。メディエーター変数は、介入群と KPI 間の因果経路に存在します。つまり、KPI に因果効果があり、介入群の因果的な影響を受けます。メディエーター変数はコントロール変数として含めないでください。含めた場合、介入群変数に対する因果推論の推定にバイアスが生じます。
変数タイプ間の因果関係は、KPI に及ぼすメディアの因果効果を把握することを目的として、次の因果関係の有向非巡回グラフ(DAG)で説明されています。ノード名の番号 1 は期間 1 の変数値、2 は期間 2 の変数値を表しています。この図には期間 1 と 2 のノードのみが表示されていますが、 \(T\) のように、期間は多数あるものとします。
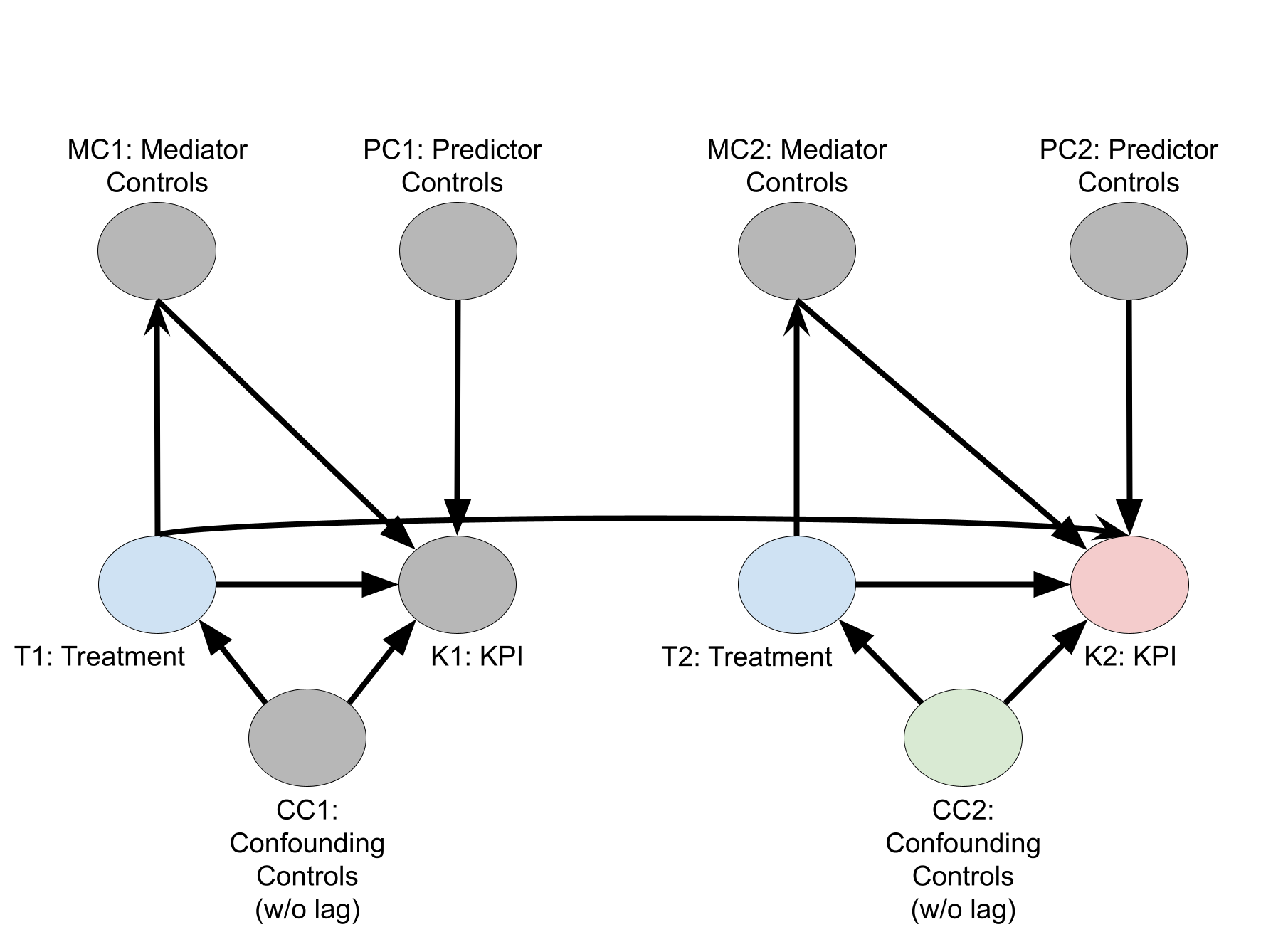
コントロール変数の選択
マーケティング ミックス モデリング(MMM)の目的は、予測精度ではなくメディア効果の因果推論です。したがって、コントロール変数の主な目的は、KPI に対する介入群の因果効果の推論を改善することです。サンプル内またはサンプル外の予測精度を向上させる可能性がある、すべての予測変数を含める必要はありません(推奨もされません)。予測精度がわずかに改善しても、因果推論の精度が向上するとは限りません。予測変数が多すぎると、因果推定値の分散が大きくなり、モデルの誤指定バイアスのリスクが高まる可能性があります。
モデルに含める可能性のある交絡変数についてブレインストーミングする際は、マーケティングの意思決定に影響する変数か、意思決定者に影響を及ぼす変数の特定に重点を置くことをおすすめします。マーケティングの意思決定に影響するほとんどの変数は KPI にも影響するため、交絡因子となることがその理由です。逆に、KPI に影響する変数の包括的なリストを作成することはほぼ不可能です。そのような変数は、マーケティングの意思決定にも影響するのでない限り、交絡因子にはなりません。
原則としてマーケティング マネージャーは、予算決定の根拠となった定量化可能なすべての情報のリストを提出できますが、実際には完全なリストを作成するのは難しい場合があります。マーケティング マネージャーへの基本的な質問としては、次のようなものがあります。
- 年間または四半期単位で、メディアの合計予算をどのように決定しましたか?
- メディア チャネル間の配分はどのように決定しましたか?
- 各年の中で、予算の多い週と少ない週をどのように決めましたか?
- 休日や商品のリリースなど、特定のイベントに応じて費用が急増していますか?
- 質問 1~4 で、予算の決定に最も影響したデータソースはどれですか?(例: 前年の KPI の値、経済関連の変数)
- オーガニック メディアはありましたか?オーガニック メディアで広告を掲載するという決定に影響を与えた要因は何ですか?
- 価格変更やプロモーションなど、メディア以外の介入群はありましたか?そうした変更を適用する時期と方法をどのように決めましたか?
コントロール変数についての推奨事項は次のとおりです。
- 交絡変数を含めます。
- メディエーター変数を除外します。
- 因果推定値の分散を低減できる重要な予測指標を含めます。
- 予測精度を最適化することだけを目的として、過度に多くの変数を含めないでください。モデルの誤指定バイアスのリスクが高まる可能性があります。
コントロール係数の事前分布および事後分布のサンプルを抽出する
コントロール係数の事前分布サンプルと事後分布サンプルはメリディアン オブジェクトに格納され、抽出して期間やその他の概要指標を作成できます。これにより、関連性の高いコントロールを特定できます。
メリディアンオブジェクトの名前が mmm の場合、コントロール係数の事前分布および事後分布のサンプルは、それぞれ mmm.inference_data.prior.gamma_c と mmm.inference_data.posterior.gamma_c で確認できます。
検索ボリュームをコントロール変数として含める
コントロール変数の選択で説明したように、介入群が KPI に及ぼす因果効果のバイアスを取り除くには、交絡変数を含める必要があります。バイアスのない因果推定を行うには、メディエーター変数を除外することも必要です。検索ボリュームは、一部のメディア チャネルではメディエーターである一方、他のメディア チャネルでは交絡因子になる可能性があります。たとえば、関連性の高い検索語句は検索広告の前提条件となることが多いため、検索ボリュームは確実に検索広告の交絡因子になります。ただし、他の種類のメディアが検索行動を促進する可能性もあるため、そうしたメディア チャネルの場合は、検索ボリュームはメディエーターとなります。詳しくは、有料検索のモデリングをご覧ください。
すべての介入群の合同効果を推定することが目的であるため、推論には単一のモデルを使用します。そのため、仮定として、検索ボリュームを交絡因子と判断してモデルに含めるか、メディエーターと判断してモデルから除外するかを決める必要があります。どちらの仮定を選ぶか決める際のポイントは次のとおりです。
- バイアスのない推定値を得るうえで重要度の高いチャネル
- 介入群、検索ボリューム、KPI の想定される相関性の強さ
- 検索ボリュームがメディエーター変数ではなく交絡変数であるチャネルの推定数
検索ボリュームと検索メディアの相関性は比較的強いため、検索ボリュームが交絡因子であると仮定してモデルに含めることが、多くの場合は正しい判断になります。ただし、この判断はユースケースによって異なります。
遅延変数を使用する
特定のコントロール変数 \(Z\)の場合は、遅延の値を含めることが有効なことがあります。たとえば、各週 \(t\)で、 \(L\)の値に \(Z_{t-1},\dots ,Z_{t-L}\)を含めます。遅延の値 \(t-1, \dots ,t-L\) が \(t\)週目の KPI に因果効果をもたらすと考えられる場合にのみ、この方法を使用することをおすすめします。
遅延のコントロールが不要な場合
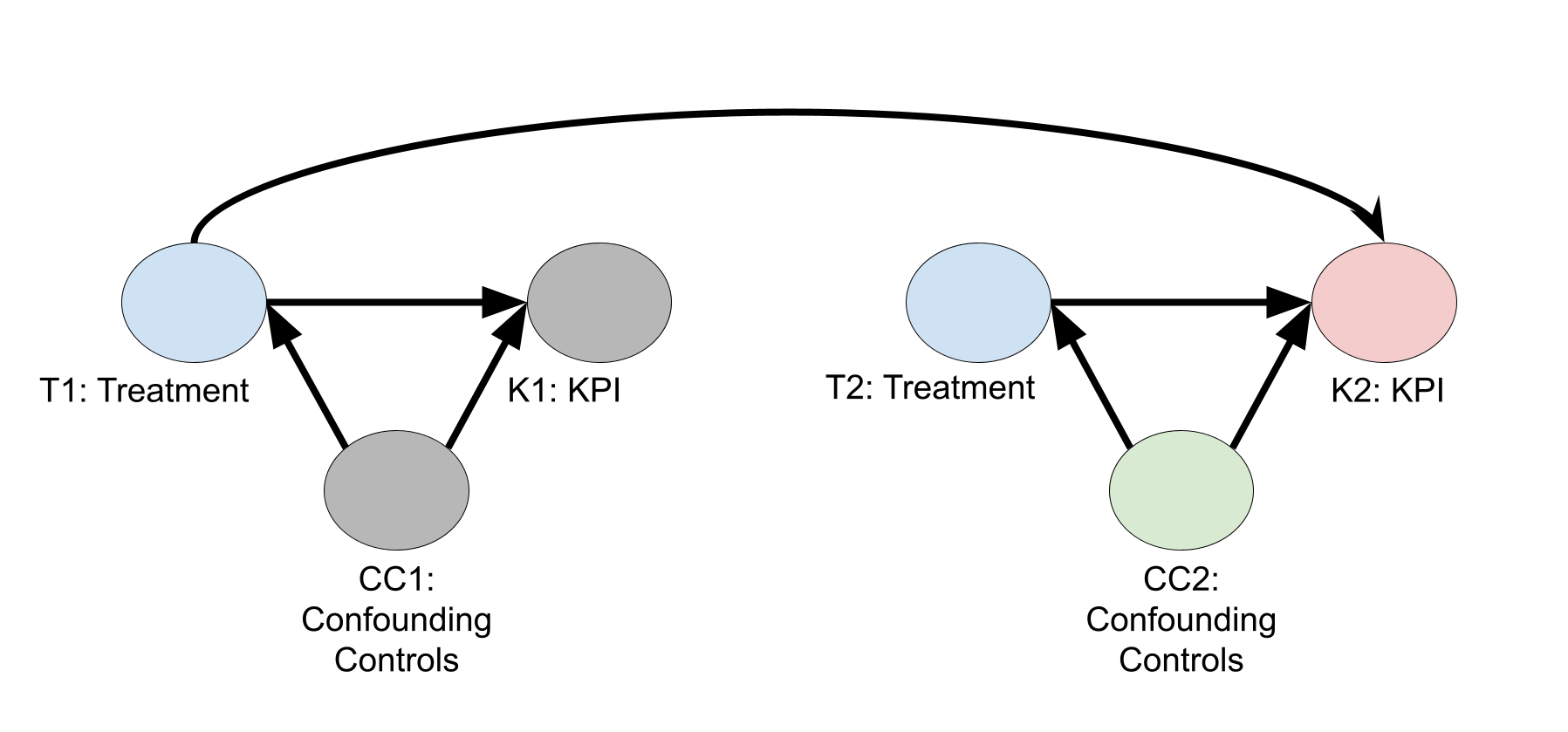
次の図は、介入群に遅延効果があり、対照群には遅延効果がないことを前提とした因果関係の有向非巡回グラフ(DAG)です。この DAG を前提とすると、遅延のコントロールは必要ありません。ノード名の番号 1 は期間 1 の変数値、2 は期間 2 の変数値を表します。この図には期間 1 と 2 のノードのみが表示されていますが、 \(N\) のように、期間は多数あるものとします。
バックドア基準(Pearl, J.、2009 年)を使用する場合、回帰モデルを適合させて\(E\bigl( K2 \big| T2,T1,C2 \bigr) = E\bigl( K2^{(T2, T1)} \big| C2 \bigr)\)を推定することで、介入群が 2 週目の KPI に及ぼす因果効果を推定できます。以前のコントロール(\(C1\))は必要ありません。
遅延のコントロールが必要な場合
次の図は、遅延のコントロールが必要な因果関係の DAG です。ここでも、ノード名の番号は期間に対応しています。介入群が 2 週目の KPI に及ぼす因果効果を推定するには、KPI に対する遅延効果がある 1 週目のコントロール変数を条件にする必要があります。それをしないと、ブロックされていないパス \(T1 \leftarrow L1 \rightarrow K2\)が残ります。バックドア基準を利用することで、回帰モデルを適合させて \(E\bigl( K2 \big| T2,T1,C2,L2,L1 \bigr) = E\bigl( K2^{(T2,T1)} \big| C2,L2,L1 \bigr)\)を推定できます。
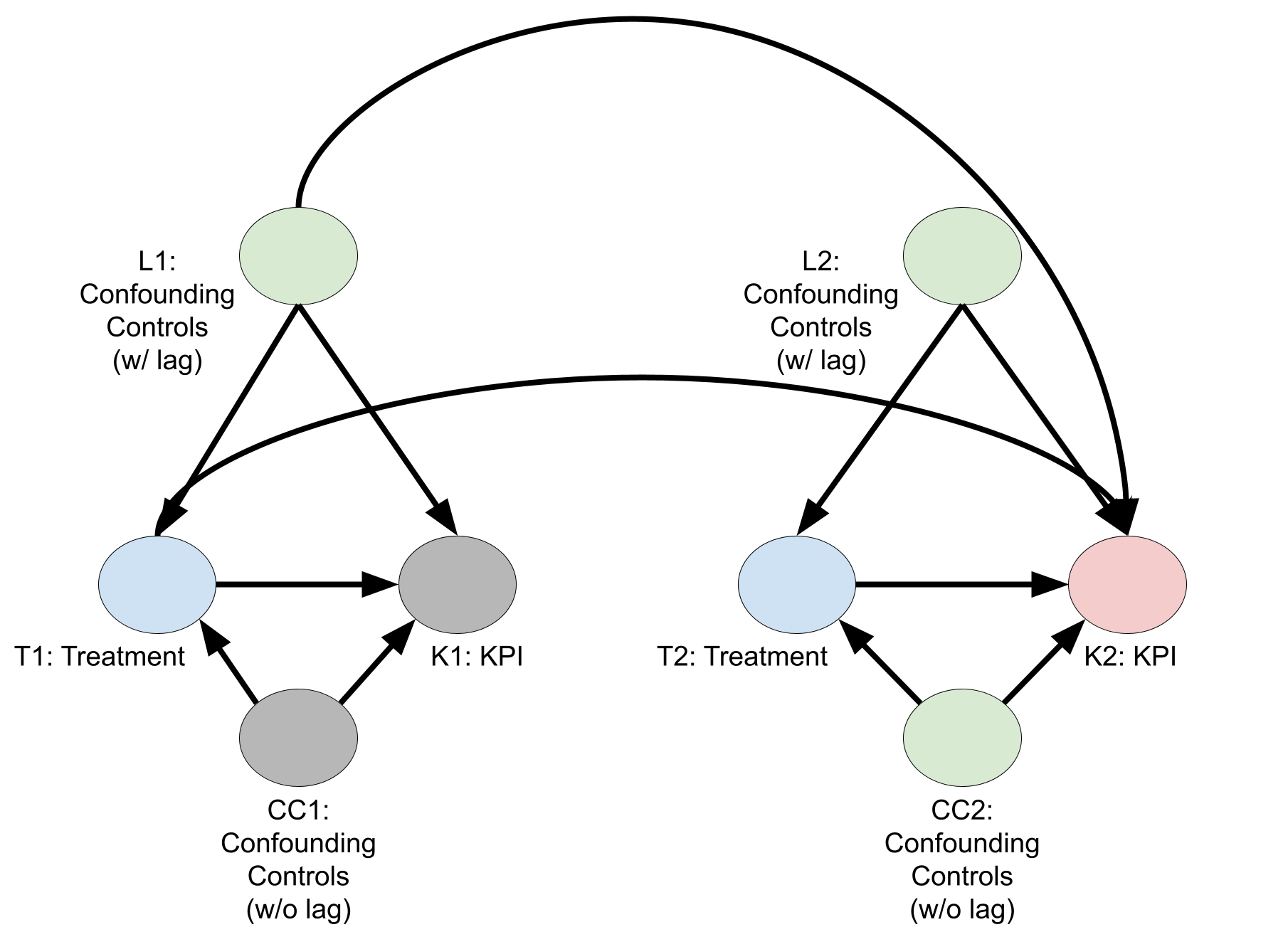
上の図は 2 週間の DAG の簡略版ですが、一般に、各週\(t\)で、 \(t,t-1, \dots ,t-L\)週目のコントロールを含める必要があります。ここで、\(L\) は、コントロールが KPI に影響を与えると考えられる最長の遅延です。 \(L\) の値はコントロール変数によって異なる場合があります。
実際には、 \(L\) を妥当な値で切り捨てることで、変数を追加しすぎてモデル分散が増大するのを防ぐことができます。遅延効果が比較的弱いのであれば、多くの場合は遅延のコントロールは完全に無視できます。このタイプのモデルの簡略化は、バイアスと分散のトレードオフと見なすことができます。
人口のスケーリング コントロール変数
デフォルトでは、KPI と有料およびオーガニック メディア施策は人口でスケーリングされます。コントロール変数は、デフォルトでは人口でスケーリングされません。気温などの一部のコントロールは、人口でスケーリングすべきでないからです。ただし、コントロール変数によっては(競合他社のインプレッション数など)、人口でスケーリングされた KPI とメディア変数との相関を最大化するために、人口でスケーリングすべきものもあります。このような変数は、ModelSpec の control_population_scaling_id 引数を使用してスケーリングできます。同様に、メディア以外の介入群もデフォルトではスケーリングされません。このような変数は、ModelSpec の non_media_population_scaling_id を使用してスケーリングできます。
対照群に因果推論やベースラインの分解がない理由
メリディアンでは、有料メディア、オーガニック メディア、メディア以外の介入群について、因果効果と貢献度(%)を確認できます。因果グラフによると、これらの変数タイプの回帰効果は因果効果として解釈できます。ただし、対照群変数の回帰効果を因果効果として解釈することはできません。そのため、メリディアンは対照群変数の因果効果や貢献度を推定しません。
メリディアンはまた、ベースラインの結果を対照群変数別の割り当て率に分解しません。一部のコントロール変数が、他のコントロール変数よりもモデルの予測精度に大きく影響するのは事実です。ただしこれは、想定される結果の計算における各変数の加算要素よりも、想定される結果の推定に各変数が寄与する分散に関係しています。実際には、コントロール変数に対してベースラインの成果の割り当てがどのように定義されるかは明確ではありません。考えられる定義の一つとして、各コントロール変数が地域と期間ごとに 0 に設定された場合に生じる、想定される結果の変化があります。ただしこの量は、コントロール変数の因果効果も予測的重要性も表していないため、実用的な意味はありません。さらに 0 という値は、すべてのコントロール変数で実質的に意味がない(または不可能である)可能性があり、解釈がさらに不明確になります。
変数には、想定される結果の計算において大きな係数と加算要素が含まれる可能性がありますが、KPI の予測因子としての重要性はほぼありません。これは、分散の小さい変数に特に当てはまります。このような変数をモデルから除外しても、加算効果を切片に吸収できる場合は、想定される結果の推定値にほとんど影響しません。
これらの変数の種類について詳しくは、オーガニック メディアとメディア以外の介入群変数をご覧ください。
