Em geral, a mídia tem um efeito de defasagem no KPI, indicando que os efeitos diminuem gradualmente com o tempo. Para modelar esse efeito, transformamos a execução de mídia de um determinado canal usando a função de Adstock:
em que:
\(w(s; \alpha) \) é uma função de peso não negativo,
\(x_s \geq 0\) é a execução de mídia no tempo \(s\),
\(\alpha\ \in\ [0, 1]\) é o parâmetro de decaimento e
\(L\) é a duração máxima da defasagem.
O Meridian oferece duas curvas de decaimento: geométrica e binomial. A taxa em que a redução gradual do efeito de mídia ocorre é determinada pela escolha da função e pelo parâmetro Alfa aprendido. O parâmetro adstock_decay_spec de ModelSpec define qual função ou combinação de funções será usada.
Por exemplo, para usar o decaimento binomial em todos os canais, opte por:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec='binomial'
)
Para usar a combinação binomial, geométrica e binomial para três canais chamados "Channel0", "Channel1" e "Channel2", respectivamente, especifique:
from meridian.model import spec
model_spec = spec.ModelSpec(
adstock_decay_spec=dict(
Channel0='binomial',
Channel1='geometric',
Channel2='binomial',
)
)
Em geral, recomendamos usar o decaimento binomial quando você considera que uma proporção significativa dos efeitos de defasagem de um canal de mídia permanece na segunda metade da janela de efeito. Caso contrário, recomendamos usar o decaimento geométrico.
Essas funções definem pesos \(w(s; \alpha)\) para a função de Adstock. Elas são determinadas de modo que, no momento \(t\), a execução de mídia no momento \(t-s\) tenha peso \(w(s; \alpha) / \sum_{s\in{\{0, ..., L\}}}w(s; \alpha)\). Para mais detalhes sobre a função de Adstock, consulte Saturação e defasagem de mídia.
Decaimento geométrico
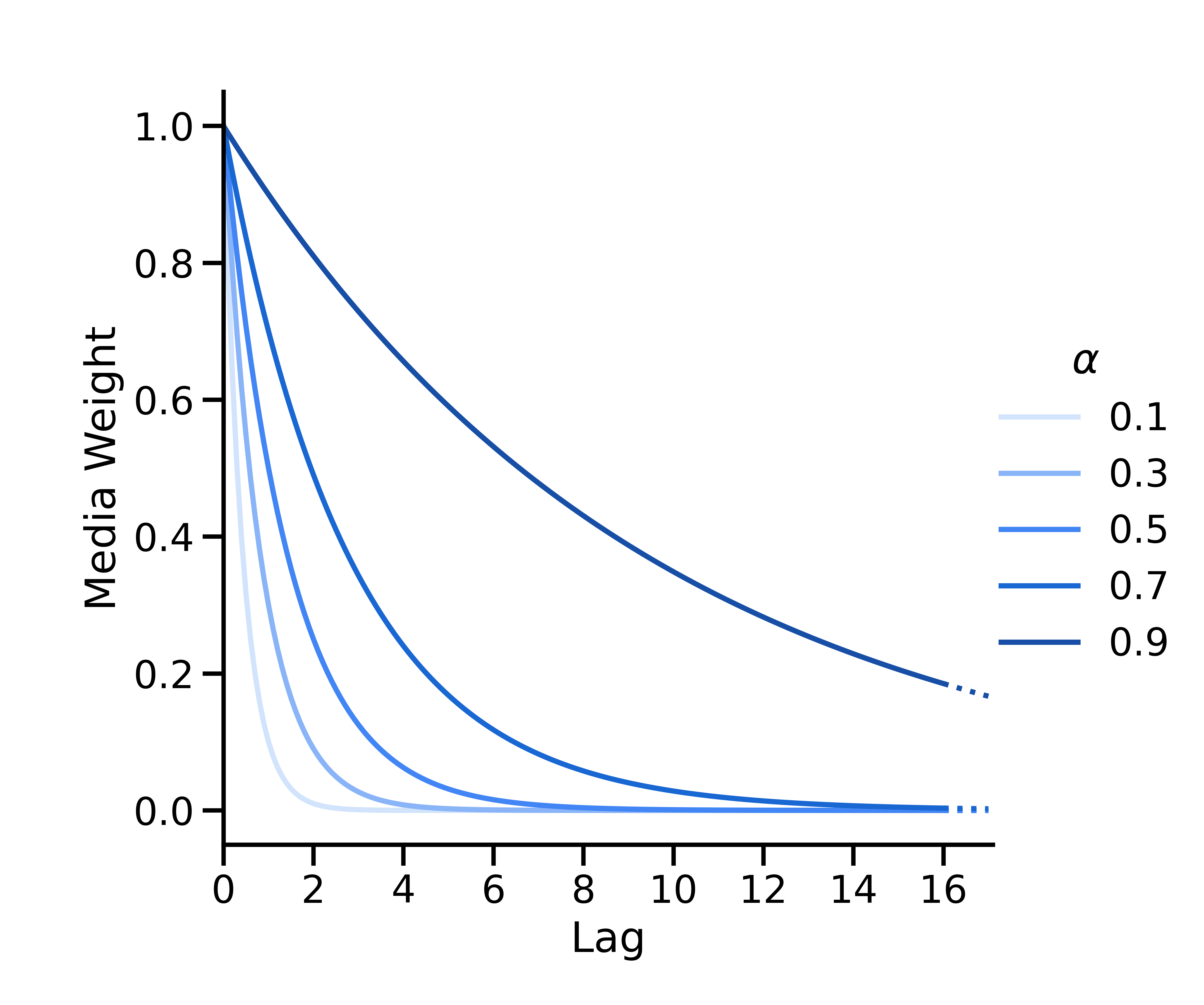
O decaimento geométrico é parametrizado como \(w(s; \alpha) = \alpha^s\), em que\(\alpha \in [0, 1] \) é o parâmetro geométrico que indica a taxa de decaimento e\(s\) é a defasagem. No momento \(t\), a execução de mídia no momento \(t-s\) tem peso \(w(s; \alpha) = \alpha^s\), que é normalizado para que todos os pesos somem um.
Decaimento binomial
O decaimento binomial é parametrizado como
em que \(L\) é a defasagem máxima (o parâmetro max_lag de ModelSpec). O mapeamento \(\alpha_*=\frac{1}{\alpha} - 1\) é usado para mapear valores de\(\alpha\) de \([0, 1]\) para \([0, \infty)\).
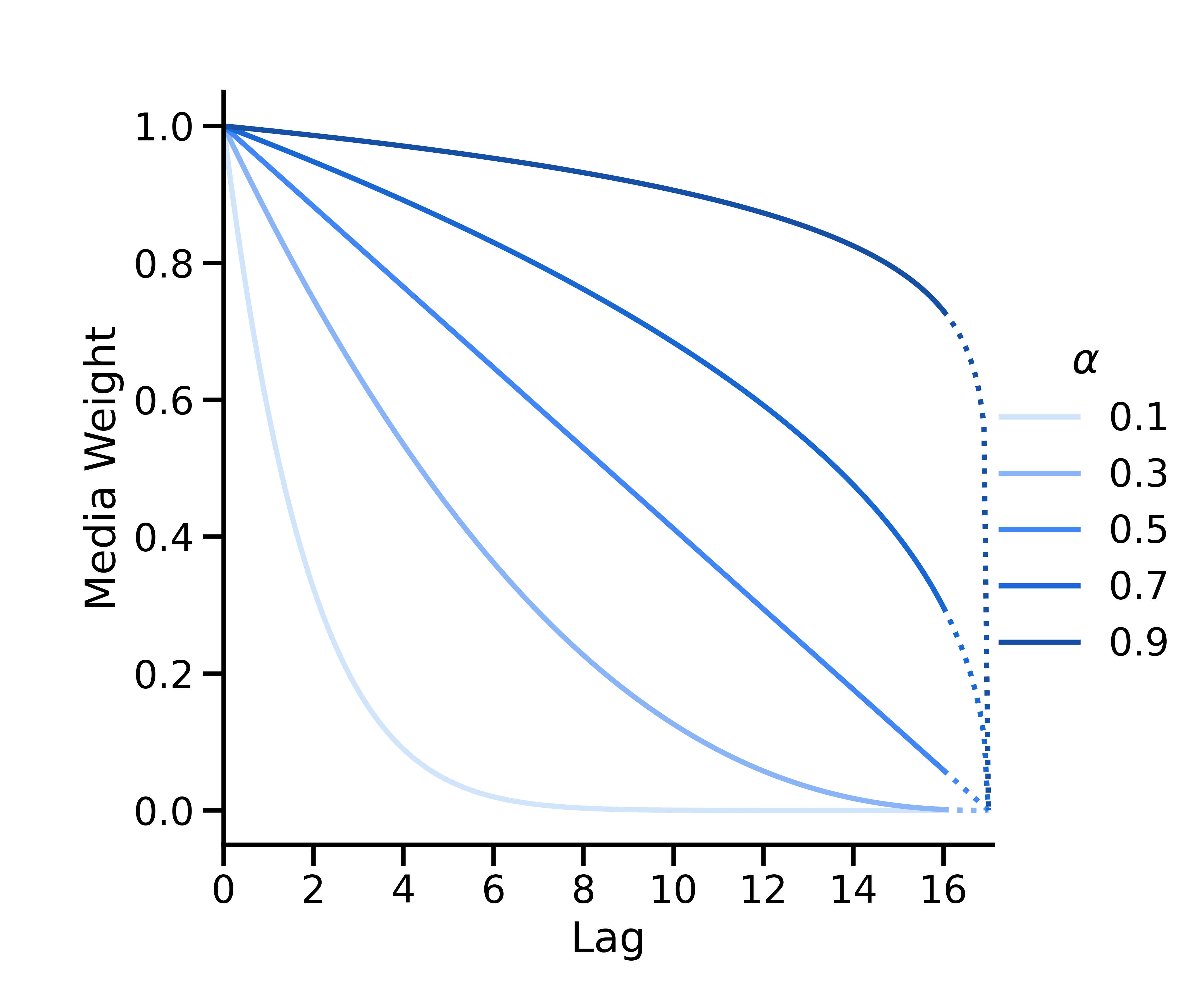
A curva binomial é convexa se \(\alpha < 0.5\), linear se \(\alpha = 0.5\)e côncava se \(\alpha > 0.5\). Ela é definida de forma que a interceptação no eixo x esteja sempre em \(L + 1\).
Decidir entre decaimento geométrico e binomial
Recomendamos selecionar o decaimento binomial quando você considera que um canal tem uma proporção significativa de efeitos na segunda metade da janela de efeito. Caso contrário, escolha o decaimento geométrico.
A curva de decaimento afeta os pesos relativos da mídia defasada. Aumentar o peso relativo dos períodos posteriores necessariamente diminui o peso relativo dos períodos anteriores. A curva de decaimento binomial define pesos que são reduzidos até zero de forma mais gradual do que a curva geométrica. Portanto, a curva binomial incentiva uma proporção maior do efeito total de mídia de um canal a acontecer em períodos posteriores, enquanto a curva geométrica incentiva uma proporção maior do efeito total de mídia de um canal a acontecer em períodos anteriores. A curva de decaimento binomial é uma boa opção ao usar valores maiores de max_lag porque ela é "esticada" para cobrir a janela de efeito, já que a interceptação no eixo x está sempre em \(L + 1\). Consulte Definir o parâmetro max_lag para mais detalhes.
Pode ser tentador selecionar a curva de decaimento binomial para todos os canais devido à capacidade de oferecer suporte a valores de max_lag maiores. No entanto, nem todos os canais terão a melhor modelagem com a curva binomial, que é mais adequada quando você considera que um canal tem uma proporção significativa de efeitos na segunda metade da janela de efeito. A aplicação incorreta da curva de decaimento binomial pode resultar em uma subestimação dos efeitos de curto prazo.
| Função | Geométrica | Binomial |
|---|---|---|
| Ideal para | Mídia com efeitos de curta duração. | Mídia com efeitos que permanecem até a segunda metade da janela de efeito. |
| Formato de curva | Decaimento rápido. | Pode permanecer por mais tempo antes de decair. |
| Recomendação de defasagem máxima | 2 a 10 períodos. | 4 a 20 períodos. |
| Desvantagens | Vulnerável à subestimação do efeito de longo prazo. | Vulnerável à subestimação do efeito de curto prazo. |
Considerações sobre efeitos de longo prazo
Se você espera efeitos de longo prazo que não estão se materializando em um modelo, alguma combinação da curva de decaimento binomial, pode ser útil modificar a distribuição a priori em Alfa e mudar o max_lag. Use as curvas de distribuição a priori de MediaEffects.plot_adstock_decay para conferir como max_lag, a distribuição a priori Alfa e a função de decaimento interagem entre si. Depois, é possível ajustar esses valores para alinhar um modelo às suas proposições iniciais sobre efeitos de defasagem. É possível modificar a distribuição a priori e max_lag simultaneamente ou em vez de selecionar uma função de decaimento específica. Recomendamos testar diferentes combinações para equilibrar a convergência, o ajuste do modelo e a janela de efeito. Consulte Definir o parâmetro max_lag para mais detalhes sobre como selecionar um valor de max_lag.
A distribuição a priori Alfa
A distribuição a priori Alfa padrão no Meridian é \(U(0, 1)\), que é uma distribuição a priori não informativa para funções de decaimento geométrico e binomial. Se você tiver uma ideia da taxa em que o efeito de mídia diminui para um canal específico, defina uma distribuição a priori Alfa personalizada nesse canal para informar o Meridian sobre sua perspectiva.
Para o decaimento geométrico e binomial, há uma relação monotônica entre\(\alpha\) e a taxa de decaimento do efeito da mídia: quanto menor for \(\alpha\), mais rápido será o decaimento, e quanto maior for \(\alpha\) , mais curto será o decaimento. As funções geométrica e binomial maximizam os efeitos de curto prazo quando \(\alpha=0\), caso em que não há efeitos defasados, e maximizam os efeitos de longo prazo quando \(\alpha=1\), caso em que toda a mídia na janela defasada histórica é ponderada igualmente.
Por isso, recomendamos definir uma distribuição a priori em Alfa com mais massa perto de zero para incentivar um decaimento mais rápido e efeitos de prazo mais curto. Por exemplo, uma distribuição Beta(1, 3) tem mais massa perto de zero do que a distribuição uniforme padrão. Por outro lado, recomendamos definir uma distribuição a priori com mais massa perto de um para incentivar um decaimento mais lento e efeitos de prazo mais longo. Por exemplo, uma distribuição Beta(3, 1) tem mais massa perto de um do que a distribuição uniforme padrão. Recomendamos representar as distribuições a priori dos pesos de Alfa e mídia (usando MediaEffects.plot_adstock_decay) para confirmar se as distribuições a priori personalizadas correspondem à sua perspectiva.
O mapa \(\alpha\) binomial
O mapeamento \(\alpha_*: [0, 1]\rightarrow[0, \infty) \) é realizado porque a função binomial decai para \(\alpha_* \in [0, \infty)\) , e a geométrica, para \(\alpha \in [0, 1]\). Esse mapeamento permite que as distribuições a priori definidas no intervalo \([0, 1]\) sejam traduzidas corretamente para \([0, \infty)\) no caso binomial e mantenham a consistência da especificação do modelo com decaimento geométrico. Valores baixos de Alfa implicam decaimento rápido e efeitos de prazo mais curto, enquanto valores mais altos de Alfa implicam decaimento lento e efeitos de prazo mais longo.
Opção avançada: defina uma distribuição a priori personalizada diretamente em \(\alpha_*\) ao usar binomial
O Meridian usa uma distribuição a priori padrão de \(U(0, 1)\) em \(\alpha\) para funções geométricas e binomiais. Com o decaimento binomial, uma distribuição a priori de \(U(0, 1)\) em\(\alpha\) é equivalente a uma distribuição a priori de Lomax(1, 1) em \(\alpha_*\):

Essa é uma distribuição a priori relativamente não informativa para permitir que os dados informem a taxa de decaimento com decaimento binomial.
O Meridian espera que as distribuições a priori \(\alpha\) personalizadas tenham suporte de \([0, 1]\) (por exemplo, uma distribuição Beta), que será mapeada para os números reais não negativos com \(1/x-1\). No entanto, se você quiser definir uma distribuição a priori em \(\alpha_*\) com suporte de \([0, \infty)\) , faça isso e transforme com o mapeamento inverso \(\frac{1}{1+x}\). Esse mapeamento está disponível pelo método auxiliar adstock_hill.transform_non_negative_reals_distribution.
Por exemplo, para ter uma distribuição a priori lognormal em \(\alpha_*\) com uma média de 0,5 e uma variância de 0,5:
import tensorflow as tf
# Example: pick mu, sigma so that the mean, variance of alpha_* are both 0.5
mu = -tf.math.log(2.0) - 0.5 * tf.math.log(3.0)
sigma = tf.math.sqrt(tf.math.log(3.0))
alpha_star_prior = tfp.distributions.LogNormal(mu, sigma) # prior on alpha_* for binomial
alpha_prior = adstock_hill.transform_non_negative_reals_distribution(alpha_star_prior)
prior = prior_distribution.PriorDistribution(
alpha_m=alpha_prior
)
model_spec = spec.ModelSpec(
prior=prior,
adstock_decay_spec='binomial'
)
Em seguida, você também pode consultar a distribuição a priori Alfa diretamente. Por exemplo, para conferir a função de densidade de probabilidade em Alfa:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, alpha_prior.prob(x), linewidth=3)
ax.set(xlabel='Alpha', ylabel='Probability')
plt.show()

Este gráfico mostra a distribuição a priori em \(\alpha\) que leva a uma distribuição a priori lognormal em\(\alpha_*\) com média e variância de 0,5 e 0,5, respectivamente.
