Nous sommes maintenant sur LinkedIn : pour consulter des informations et des ressources de Google Search Central sur la découvrabilité de votre site, suivez-nous sur LinkedIn.

Données structurées du solutionneur mathématique (`MathSolver`)

Pour aider les élèves, les enseignants et toute autre personne intéressée à résoudre un problème de mathématiques, vous pouvez ajouter des données structurées afin d'indiquer le type de problème, ainsi que des liens vers les procédures de résolution de problèmes de mathématiques spécifiques. Voici comment les solutions mathématiques peuvent s'afficher dans les résultats de recherche Google (notez toutefois que l'apparence peut changer) :

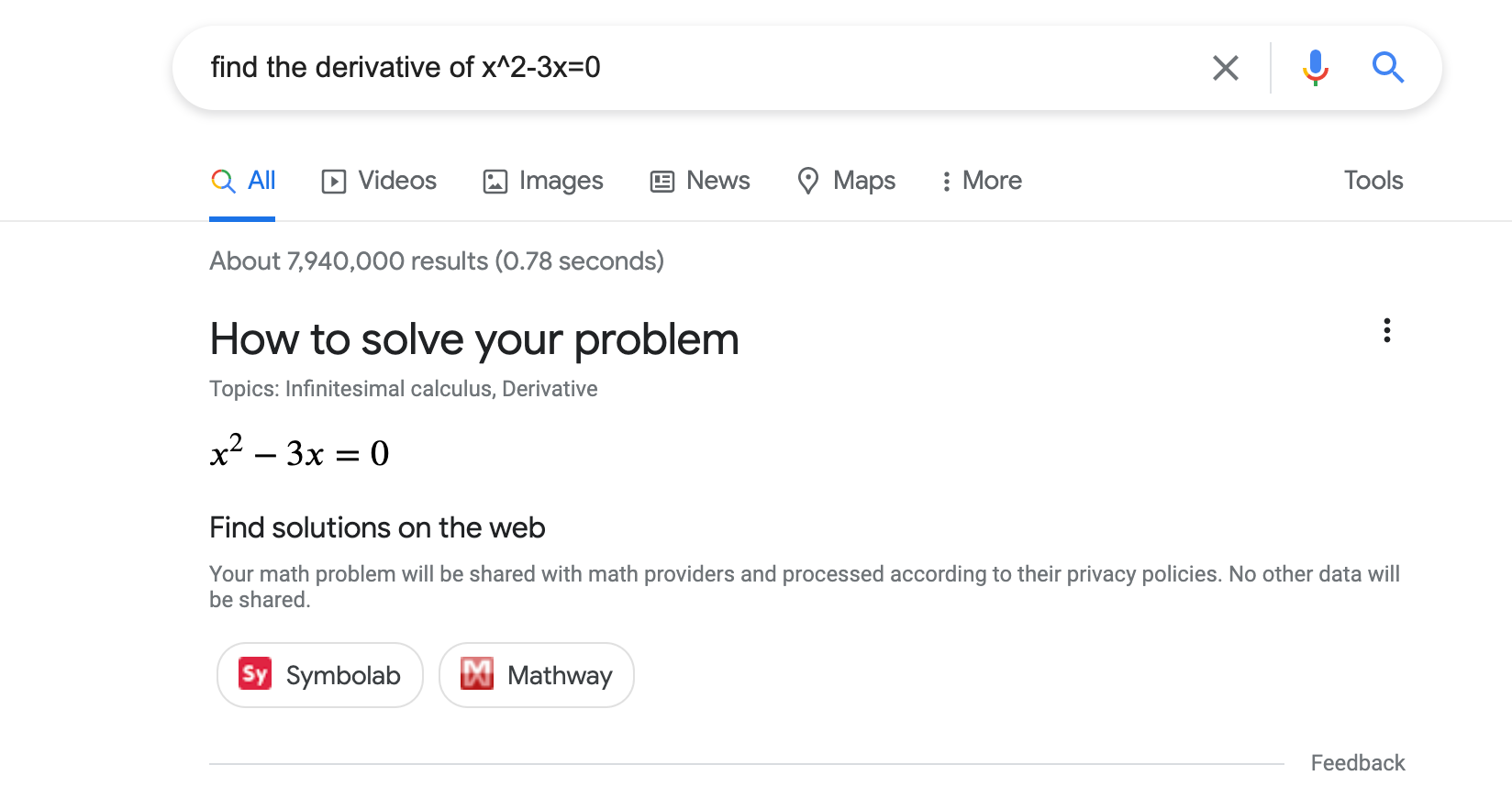
$Exemple de résultat enrichi de solutions mathématiques$

Comment ajouter des données structurées

Ces données structurées représentent un format normalisé permettant de fournir des informations sur une page et de classer son contenu. En savoir plus sur le fonctionnement des données structurées

Voici, dans les grandes lignes, comment créer, tester et publier des données structurées. Pour consulter un guide détaillé sur l'ajout de données structurées à une page Web, accédez à cet atelier de programmation.

Ajoutez les propriétés obligatoires. En fonction du format que vous utilisez, découvrez où insérer des données structurées sur la page.
Vous utilisez un CMS ? Il est peut-être plus simple d'utiliser un plug-in intégré à votre CMS.
Vous utilisez JavaScript ? Découvrez comment générer des données structurées avec JavaScript.
Suivez les consignes.
Validez votre code à l'aide de l'outil de test des résultats enrichis et corrigez les erreurs critiques, le cas échéant. Envisagez également de résoudre les problèmes non critiques que l'outil a pu signaler, car cela peut contribuer à améliorer la qualité de vos données structurées. Toutefois, ce n'est pas nécessaire pour pouvoir bénéficier des résultats enrichis.
Déployez quelques pages où figurent vos données structurées et utilisez l'outil d'inspection d'URL pour découvrir comment Google voit la page. Assurez-vous que Google peut accéder à votre page et qu'elle n'est pas bloquée par un fichier robots.txt, la balise noindex ni par des identifiants de connexion. Si tout semble être en ordre, vous pouvez demander à Google d'explorer de nouveau vos URL.
Remarque : prévoyez un certain temps avant que la nouvelle exploration et la nouvelle indexation soient effectuées. Gardez à l'esprit qu'il faut souvent compter plusieurs jours après la publication d'une page pour que Google puisse la trouver et l'explorer.
Pour informer Google des modifications futures de vos pages, nous vous recommandons de nous envoyer un sitemap. Vous pouvez automatiser cette opération à l'aide de l'API Sitemap de la Search Console.

Exemples

Action de résolution unique

Voici un exemple de page d'accueil d'une solution mathématique proposant une seule action de résolution d'équations polynomiales et de problèmes dérivés. Elle est disponible en anglais et en espagnol.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
[
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "An awesome math solver",
    "url": "https://www.mathdomain.com/",
    "usageInfo": "https://www.mathdomain.com/privacy",
    "inLanguage": "en",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  },
  {
    "@context": "https://schema.org",
    "@type": ["MathSolver", "LearningResource"],
    "name": "Un solucionador de matemáticas increíble",
    "url": "https://es.mathdomain.com/",
    "usageInfo": "https://es.mathdomain.com/privacy",
    "inLanguage": "es",
    "potentialAction": [{
      "@type": "SolveMathAction",
      "target": "https://es.mathdomain.com/solve?q={math_expression_string}",
      "mathExpression-input": "required name=math_expression_string",
      "eduQuestionType": ["Polynomial Equation","Derivative"]
     }],
    "learningResourceType": "Math solver"
  }
]
</script>
</body>
</html>

Le balisage espagnol peut être placé directement sur https://es.mathdomain.com/ au lieu de l'ajouter avec la version anglophone du balisage du solutionneur mathématique.

Deux actions de résolution

Voici un exemple de page d'accueil d'une solution mathématique proposant deux actions de résolution : une action pour résoudre des équations polynomiales, et une autre pour les équations trigonométriques. Elle n'est disponible qu'en anglais.

<html>
<head>
<title>An awesome math solver</title>
</head>
<body>
<script type="application/ld+json">
{
  "@context": "https://schema.org",
  "@type": ["MathSolver", "LearningResource"],
  "name": "An awesome math solver",
  "url": "https://www.mathdomain.com/",
  "usageInfo": "https://www.mathdomain.com/privacy",
  "inLanguage": "en",
  "potentialAction": [{
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/solve?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Polynomial Equation"
   },
   {
     "@type": "SolveMathAction",
     "target": "https://mathdomain.com/trig?q={math_expression_string}",
     "mathExpression-input": "required name=math_expression_string",
     "eduQuestionType": "Trigonometric Equation"
   }],
  "learningResourceType": "Math solver"
}
</script>
</body>
</html>

Consignes

Pour que les solutions mathématiques proposées par votre page puissent apparaître sous forme de résultats enrichis, vous devez respecter les consignes suivantes :

Consignes techniques

Ajoutez des données structurées MathSolver à la page d'accueil de votre site.
Assurez-vous que Googlebot peut explorer votre site efficacement.
Si plusieurs versions identiques de la même solution mathématique sont hébergées sous des URL différentes, utilisez les URL canoniques sur chaque version de la page.
Nous n'autorisons pas les solutions mathématiques uniquement accessibles via un paywall ou via la saisie d'identifiants de connexion. Une fois que les utilisateurs accèdent à votre site à partir de la fonctionnalité Google, ils doivent avoir directement accès à la solution et à la procédure de résolution de leur problème initial. Vous pouvez toutefois proposer tout contenu supplémentaire via un paywall ou des identifiants de connexion.

Consignes relatives au contenu

Nous avons créé des consignes spécifiques au contenu des solutions mathématiques afin de nous assurer que nos utilisateurs sont exposés à des ressources d'apprentissage pertinentes. Si nous constatons que du contenu enfreint ces règles, nous prendrons les mesures appropriées, par exemple en soumettant une action manuelle et en empêchant l'affichage des pages concernées sous forme de résultats enrichis sur Google.

Nous n'autorisons pas les contenus promotionnels déguisés en solutions mathématiques, tels que ceux publiés par des tiers (programmes d'affiliation, par exemple).
Vous êtes responsable de l'exactitude et de la qualité des solutions mathématiques proposées via cette fonctionnalité. S'il ressort de nos contrôles qualité que certaines de vos données sont inexactes, une partie ou la totalité de vos solutions mathématiques peut cesser d'apparaître sous forme de résultats enrichis tant que vous n'aurez pas résolu les problèmes en fonction de leur gravité. Prêtez, entre autres, attention aux éléments suivants :
- Précision des types de problèmes que votre solution est capable de résoudre
- Précision des solutions que vous proposez pour résoudre les problèmes de mathématiques

Définitions des types de données structurées

Vous devez inclure les propriétés obligatoires pour que votre contenu puisse être affiché sous forme de résultat enrichi. Vous pouvez également inclure les propriétés recommandées pour ajouter d'autres informations à vos données structurées et ainsi offrir une meilleure expérience utilisateur.

MathSolver

MathSolver est un outil qui aide les élèves, les enseignants et toute autre personne concernée à résoudre des problèmes de mathématiques en proposant des solutions détaillées. Ajoutez des données structurées MathSolver sur la page d'accueil de votre site.

La définition complète de l'élément MathSolver est disponible sur schema.org/MathSolver.

Les propriétés prises en charge par Google sont les suivantes :

Propriétés obligatoires
`potentialAction`	`SolveMathAction` Action qui mène à l'explication mathématique (par exemple, graphique ou solution détaillée) d'une expression mathématique. { "@type": "MathSolver", "potentialAction": [{ "@type": "SolveMathAction", "target": "https://mathdomain.com/solve?q={math_expression_string}", "mathExpression-input": "required name=math_expression_string", "eduQuestionType": "Polynomial Equation" }] }
`potentialAction.mathExpression-input`	`Text` Un espace réservé pour une expression mathématique (par exemple: x^2-3x=0) envoyée par Google à votre site Web. Vous pouvez ensuite "résoudre" l'expression mathématique, ce qui peut nécessiter de la simplifier, de la transformer ou de la résoudre pour une variable spécifique. Plusieurs formats sont possibles (par exemple, LaTeX, Ascii-Math ou expressions mathématiques que vous pouvez rédiger avec un clavier). `mathExpression-input` est une propriété annotée. Pour en savoir plus, consultez la page `Potential Actions`. Pour certains types de problèmes, `math_expression_string` indique à la fois le type de problème et ses paramètres. Voici quelques exemples de types de problèmes plus complexes afin que vous puissiez les anticiper et les analyser correctement. Dérivées Google enverra une `math_expression_string` sous l'une des deux formes suivantes : (`math_expression`)' d/d`variable` `math_expression` Examples: `(x^2+x)'` `d/dx (x^2+x)` `d/dy y^2+y` Integrals Google will send a `math_expression_string` in one of two forms: \int `math_expression` \int_{`from`}^{`to`} `math_expression` Exemples : `\int x^2+x` `\int_{0}^{2} x^2+x` Limites Google enverra une `math_expression_string` sous l'une des deux formes suivantes : \lim `math_expression` \lim_{`variable`\rightarrow`value`} `math_expression` Exemples : `\lim_{x\rightarrow0} sin(x)/x` `\lim_{y\rightarrow\infty} sin(y)/y` `\lim sin(x)/x`
`url`	`URL` URL de la solution mathématique (`MathSolver`).
`usageInfo`	`URL` Règles de confidentialité de votre site de résolution des problèmes de mathématiques. { "@type": "MathSolver", "usageInfo": "https://www.mathdomain.com/privacy" }
`potentialAction.target`	`EntryPoint` Point d'entrée de la cible d'URL pour une action. La propriété `potentialAction.target` accepte une chaîne pour représenter l'expression mathématique résolue par l'action. { "@type": "MathSolver", "potentialAction": [{ "@type": "SolveMathAction", "target": "https://mathdomain.com/solve?q={math_expression_string}" }] }

Propriétés recommandées

Propriétés recommandées
`inLanguage`	`Text` Langues acceptées sur votre site de résolution de problèmes de mathématiques. Consultez ce tableau pour déterminer la liste des langues possibles. { "@type": "MathSolver", "inLanguage": "es" }
`assesses`	`Text` : liste de définitions des types de problèmes Types de problèmes résolus avec `HowTo`. Utilisez la propriété `assesses` si vous optez pour le balisage `HowTo` en plus du balisage `MathSolver`. { "@type": "MathSolver", "assesses": "Polynomial Equation" }
`potentialAction.eduQuestionType`	`Text` : liste de définitions des types de problèmes Types de problèmes pouvant être résolus par la propriété `potentialAction.target`. { "@type": "SolveMathAction", "eduQuestionType": "Polynomial Equation" }

inLanguage

Text

Langues acceptées sur votre site de résolution de problèmes de mathématiques. Consultez ce tableau pour déterminer la liste des langues possibles.

{
  "@type": "MathSolver",
  "inLanguage": "es"
}

assesses

Text : liste de définitions des types de problèmes

Types de problèmes résolus avec HowTo. Utilisez la propriété assesses si vous optez pour le balisage HowTo en plus du balisage MathSolver.

{
  "@type": "MathSolver",
  "assesses": "Polynomial Equation"
}

potentialAction.eduQuestionType

Text : liste de définitions des types de problèmes

Types de problèmes pouvant être résolus par la propriété potentialAction.target.

{
  "@type": "SolveMathAction",
  "eduQuestionType": "Polynomial Equation"
}

LearningResource

LearningResource indique que la ressource pédagogique qui fait l'objet du balisage vise à aider les élèves, les enseignants et toute autre personne souhaitant enrichir ses connaissances en la matière. Utilisez LearningResource sur la page d'accueil de votre site.

La définition complète de LearningResource est disponible sur schema.org/LearningResource.

Les propriétés prises en charge par Google sont les suivantes :

Propriétés obligatoires

Propriétés obligatoires
`learningResourceType`	`Text` Type de cette ressource pédagogique. Utilisez cette valeur fixe : `Math Solver`. { "@type": ["MathSolver", "LearningResource"], "learningResourceType": "Math Solver" }

learningResourceType