Dans ce tutoriel, vous allez découvrir la méthodologie de modélisation de la distribution des espèces à l'aide de Google Earth Engine. Nous vous présenterons brièvement la modélisation de la distribution des espèces, puis nous vous expliquerons comment prédire et analyser l'habitat d'une espèce d'oiseau en voie de disparition appelée pitta des nymphes (nom scientifique : Pitta nympha).
Exécute-moi en premier
Exécutez la cellule suivante pour initialiser l'API. Le résultat contiendra des instructions sur la façon d'accorder à ce notebook l'accès à Earth Engine à l'aide de votre compte.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Brève présentation de la modélisation de la distribution des espèces
Découvrons ce que sont les modèles de distribution des espèces, les avantages de l'utilisation de Google Earth Engine pour leur traitement, les données requises pour les modèles et la structure du workflow.
Qu'est-ce que la modélisation de la distribution des espèces ?
La modélisation de la distribution des espèces (SDM, Species Distribution Modeling) est la méthodologie la plus courante pour estimer la distribution géographique réelle ou potentielle d'une espèce. Il s'agit de caractériser les conditions environnementales adaptées à une espèce particulière, puis d'identifier où ces conditions adaptées sont réparties géographiquement.
La modélisation de la distribution des espèces (SDM) est devenue un élément essentiel de la planification de la conservation ces dernières années, et diverses techniques de modélisation ont été développées à cet effet. L'implémentation de la modélisation de la distribution des espèces dans Google Earth Engine (GEE ci-dessous) permet d'accéder facilement à des données environnementales à grande échelle, ainsi qu'à de puissantes capacités de calcul et à la prise en charge des algorithmes de machine learning, ce qui permet une modélisation rapide.
Données requises pour SDM
La SDM utilise généralement la relation entre les enregistrements d'occurrence d'espèces connues et les variables environnementales pour identifier les conditions dans lesquelles une population peut se maintenir. En d'autres termes, deux types de données d'entrée de modèle sont requis :
- Enregistrements d'occurrences d'espèces connues
- Diverses variables d'environnement
Ces données sont saisies dans des algorithmes pour identifier les conditions environnementales associées à la présence d'espèces.
Workflow de SDM utilisant GEE
Voici le workflow pour la modélisation de la distribution des espèces à l'aide de GEE :
- Collecte et prétraitement des données d'occurrence des espèces
- Définition de la zone d'intérêt
- Ajout de variables environnementales GEE
- Génération de données de pseudo-absence
- Ajustement et prédiction du modèle
- Importance des variables et évaluation de la précision
Prédiction et analyse des habitats à l'aide de GEE
La pitta ninymphe (Pitta nympha) sera utilisée comme étude de cas pour illustrer l'application de la SDM basée sur GEE. Bien que cette espèce spécifique ait été sélectionnée pour un exemple, les chercheurs peuvent appliquer la méthodologie à toute espèce cible d'intérêt en apportant de légères modifications au code source fourni.
La pitta féerique est un oiseau migrateur estival et de passage rare en Corée du Sud, dont l'aire de répartition s'étend en raison du réchauffement climatique récent sur la péninsule coréenne. Il est classé comme espèce rare, espèce sauvage en voie de disparition de classe II, monument naturel n° 204, évalué comme éteint au niveau régional (RE) dans la Liste rouge nationale et vulnérable (VU) selon les catégories de l'UICN.
La modélisation de la distribution des espèces (SDM) pour la planification de la conservation de la pitta féerique semble très utile. Passons maintenant à la prédiction et à l'analyse des habitats à l'aide de GEE.
Tout d'abord, les bibliothèques Python sont importées.L'instruction import importe l'intégralité du contenu d'un module, tandis que l'instruction from import permet d'importer des objets spécifiques à partir d'un module.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Collecte et prétraitement des données d'occurrence des espèces
Collectons maintenant les données d'occurrence pour la pitta fée. Même si vous n'avez pas accès aux données d'occurrence pour l'espèce qui vous intéresse, vous pouvez obtenir des données d'observation sur des espèces spécifiques via l'API GBIF. L'API GBIF est une interface qui permet d'accéder aux données de répartition des espèces fournies par le GBIF. Elle permet aux utilisateurs de rechercher, de filtrer et de télécharger des données, ainsi que d'obtenir diverses informations sur les espèces.
Dans le code ci-dessous, la variable species_name est associée au nom scientifique de l'espèce (par exemple, Pitta nympha pour la pitta ninphe) et la variable country_code est associée au code pays (par exemple, KR pour la Corée du Sud). La variable base_url stocke l'adresse de l'API GBIF. params est un dictionnaire contenant les paramètres à utiliser dans la requête API :
scientificName: définit le nom scientifique de l'espèce à rechercher.country: limite la recherche à un pays spécifique.hasCoordinate: garantit que seules les données avec des coordonnées (true) sont recherchées.basisOfRecord: ne sélectionne que les enregistrements d'observation humaine (HUMAN_OBSERVATION).limit: définit le nombre maximal de résultats renvoyés sur 10 000.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
À l'aide des paramètres définis précédemment, nous interrogeons l'API GBIF pour obtenir des enregistrements d'observations de la brève nymphe (Pitta nympha) et chargeons les résultats dans un DataFrame pour vérifier la première ligne. Un DataFrame est une structure de données permettant de gérer les données au format tableau, composées de lignes et de colonnes. Si nécessaire, le DataFrame peut être enregistré au format CSV et relu.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
Ensuite, nous convertissons le DataFrame en GeoDataFrame qui inclut une colonne pour les informations géographiques (geometry) et vérifions la première ligne. Un GeoDataFrame peut être enregistré en tant que fichier GeoPackage (*.gpkg) et relu.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Cette fois, nous avons créé une fonction pour visualiser la distribution des données par année et par mois à partir du GeoDataFrame, et l'afficher sous forme de graphique, qui peut ensuite être enregistré en tant que fichier image. L'utilisation d'une carte thermique nous permet de comprendre rapidement la fréquence d'apparition des espèces par année et par mois, ce qui offre une visualisation intuitive des changements et des tendances temporelles dans les données. Cela permet d'identifier les tendances temporelles et les variations saisonnières dans les données d'occurrence des espèces, ainsi que de détecter rapidement les valeurs aberrantes ou les problèmes de qualité dans les données.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
Les données de 1995 sont très éparses, avec des lacunes importantes par rapport aux autres années. Les mois d'août et de septembre présentent également des échantillons limités et des caractéristiques saisonnières différentes de celles des autres périodes. L'exclusion de ces données peut contribuer à améliorer la stabilité et le pouvoir prédictif du modèle.
Toutefois, il est important de noter que l'exclusion de données peut améliorer la capacité de généralisation du modèle, mais peut également entraîner la perte d'informations précieuses pour les objectifs de recherche. Par conséquent, ces décisions doivent être prises avec soin.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Le GeoDataFrame filtré est ensuite converti en objet Google Earth Engine.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
Ensuite, nous allons définir la taille des pixels raster des résultats SDM sur une résolution de 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Lorsque plusieurs points d'occurrence sont présents dans le même pixel raster de résolution de 1 km, il est fort probable qu'ils partagent les mêmes conditions environnementales au même emplacement géographique. L'utilisation directe de ces données dans l'analyse peut introduire un biais dans les résultats.
En d'autres termes, nous devons limiter l'impact potentiel du biais d'échantillonnage géographique. Pour ce faire, nous ne conserverons qu'un seul emplacement dans chaque pixel de 1 km et supprimerons tous les autres, ce qui permettra au modèle de refléter plus objectivement les conditions environnementales.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
La visualisation comparant le biais d'échantillonnage géographique avant (en bleu) et après (en rouge) le prétraitement est présentée ci-dessous. Pour faciliter la comparaison, la carte a été centrée sur la zone où les coordonnées de présence de la pitta féerique sont fortement concentrées dans le parc national de Hallasan.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Définition de la zone d'intérêt
La définition de la zone d'intérêt (AOI, Area of Interest) est le terme utilisé par les chercheurs pour désigner la zone géographique qu'ils souhaitent analyser. Il a une signification similaire à celle du terme "Zone d'étude".
Dans ce contexte, nous avons obtenu le cadre de sélection de la géométrie de la couche de points d'occurrence et créé une zone tampon de 50 kilomètres autour (avec une tolérance maximale de 1 000 mètres) pour définir la ZI.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
Ajout de variables environnementales GEE
Ajoutons maintenant des variables environnementales à l'analyse. GEE fournit un large éventail d'ensembles de données pour les variables environnementales telles que la température, les précipitations, l'altitude, la couverture terrestre et le relief. Ces ensembles de données nous permettent d'analyser de manière exhaustive les différents facteurs qui peuvent influencer les préférences d'habitat de la pitta féerique.
La sélection des variables environnementales GEE dans SDM doit refléter les caractéristiques de préférence d'habitat de l'espèce. Pour ce faire, il convient de mener des recherches et d'examiner la littérature existante sur les préférences d'habitat de la pitta féerique. Ce tutoriel se concentre principalement sur le workflow de la SDM à l'aide de GEE. Certains détails approfondis sont donc omis.
WorldClim V1 Bioclim : cet ensemble de données fournit 19 variables bioclimatiques dérivées des données mensuelles de température et de précipitations. Elle couvre la période allant de 1960 à 1991 et a une résolution de 927,67 mètres.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m : cet ensemble de données contient des données d'élévation numérique issues de la mission Shuttle Radar Topography Mission (SRTM). Les données ont été collectées principalement autour de l'an 2000 et sont fournies à une résolution d'environ 30 mètres (1 seconde d'arc). Le code suivant calcule les couches d'élévation, de pente, d'aspect et d'ombrage à partir des données SRTM.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Évolution de la couverture forestière mondiale (GFCC, Global Forest Cover Change) : couverture arborée pluriannuelle mondiale de 30 m : l'ensemble de données VCF (Vegetation Continuous Fields) de Landsat estime la proportion de couverture végétale projetée verticalement lorsque la hauteur de la végétation est supérieure à 5 mètres. Cet ensemble de données est fourni pour quatre périodes centrées sur les années 2000, 2005, 2010 et 2015, avec une résolution de 30 mètres. Ici, les valeurs médianes de ces quatre périodes sont utilisées.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (variables bioclimatiques), terrain (topographie) et median_tcc (couverture de la canopée) sont combinées en une seule image multibande. La bande elevation est sélectionnée à partir de terrain, et un watermask est créé pour les zones géographiques où elevation est supérieur à 0. Cela masque les régions situées sous le niveau de la mer (par exemple, l'océan) et prépare le chercheur à analyser de manière exhaustive divers facteurs environnementaux pour la ZI.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Lorsque des variables de prédiction fortement corrélées sont incluses ensemble dans un modèle, des problèmes de multicolinéarité peuvent survenir. La multicolinéarité est un phénomène qui se produit lorsqu'il existe de fortes relations linéaires entre les variables indépendantes d'un modèle, ce qui entraîne une instabilité dans l'estimation des coefficients (pondérations) du modèle. Cette instabilité peut réduire la fiabilité du modèle et rendre difficile la prédiction ou l'interprétation de nouvelles données. Nous allons donc tenir compte de la multicolinéarité et procéder à la sélection des variables de prédiction.
Nous allons d'abord générer 5 000 points aléatoires, puis extraire les valeurs des variables de prédiction de l'image multibande unique à ces points.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Nous allons convertir les valeurs de prédiction extraites pour chaque point en DataFrame, puis vérifier la première ligne.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Calcul des coefficients de corrélation de Spearman entre les variables de prédiction données et visualisation dans une carte de chaleur.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
Le coefficient de corrélation de Spearman est utile pour comprendre les associations générales entre les variables de prédiction, mais il n'évalue pas directement la façon dont plusieurs variables interagissent, en particulier pour détecter la multicolinéarité.
Le facteur d'inflation de la variance (VIF, Variance Inflation Factor) est une métrique statistique utilisée pour évaluer la multicolinéarité et guider la sélection des variables. Il indique le degré de relation linéaire de chaque variable indépendante avec les autres variables indépendantes. Des valeurs VIF élevées peuvent être la preuve d'une multicolinéarité.
En général, lorsque les valeurs VIF dépassent 5 ou 10, cela suggère que la variable présente une forte corrélation avec d'autres variables, ce qui peut compromettre la stabilité et l'interprétabilité du modèle. Dans ce tutoriel, un critère de valeurs VIF inférieures à 10 a été utilisé pour la sélection des variables. Les six variables suivantes ont été sélectionnées en fonction du VIF.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
Ensuite, visualisons les six variables de prédiction sélectionnées sur la carte.
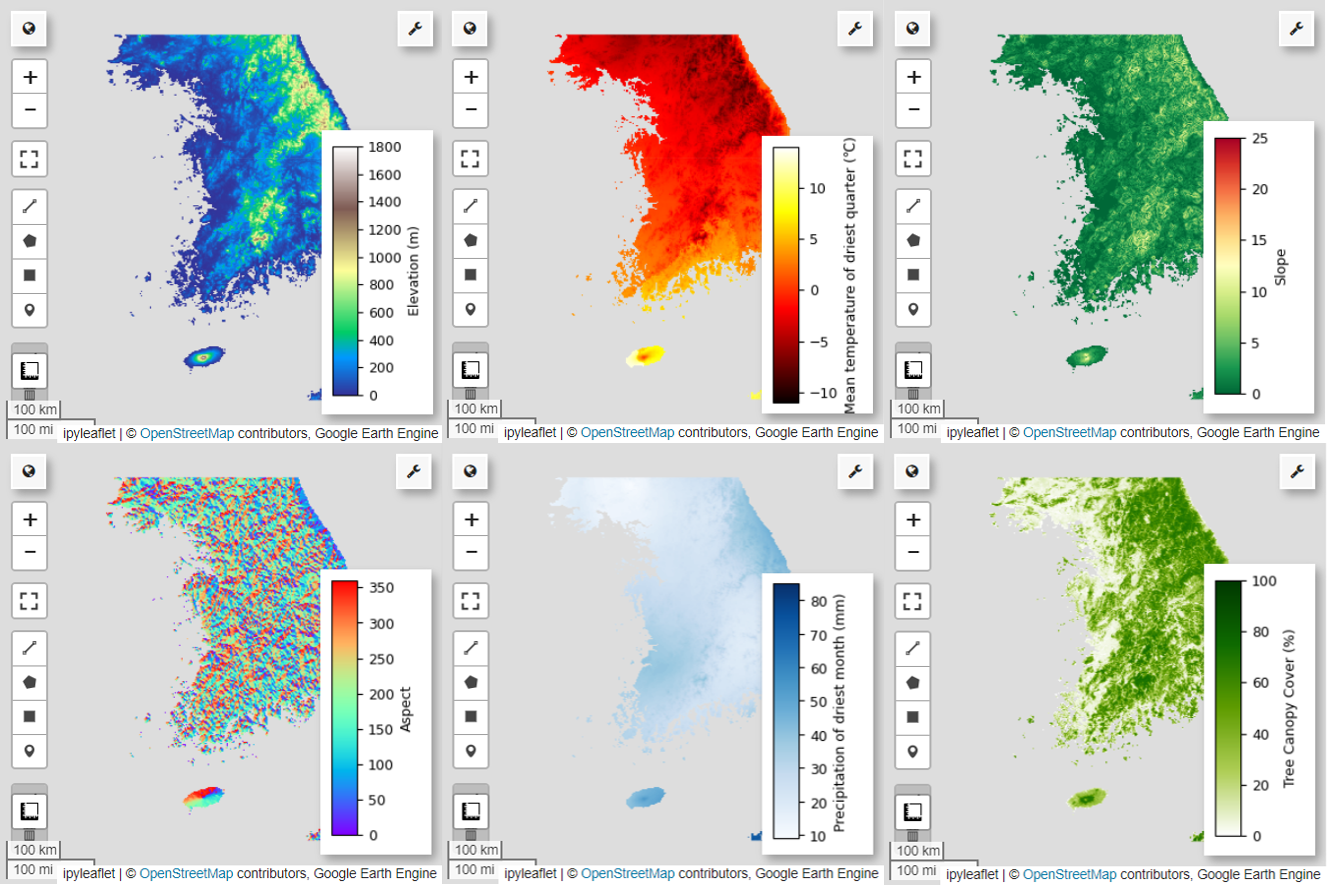
Vous pouvez explorer les palettes disponibles pour la visualisation de cartes à l'aide du code suivant. Par exemple, la palette terrain se présente comme suit :
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Génération de données de pseudo-absence
Dans le processus de modélisation de la distribution des espèces, la sélection des données d'entrée pour une espèce est principalement abordée à l'aide de deux méthodes :
Méthode de présence/arrière-plan : cette méthode compare les lieux où une espèce particulière a été observée (présence) avec d'autres lieux où elle n'a pas été observée (arrière-plan). Ici, les données de fond ne désignent pas nécessairement les zones où l'espèce n'existe pas, mais sont plutôt configurées pour refléter les conditions environnementales globales de la zone d'étude. Il permet de distinguer les environnements adaptés à l'espèce de ceux qui le sont moins.
Méthode de présence/absence : cette méthode compare les lieux où l'espèce a été observée (présence) avec ceux où elle n'a définitivement pas été observée (absence). Ici, les données d'absence représentent des lieux spécifiques où l'espèce n'existe pas. Elle ne reflète pas les conditions environnementales globales de la zone d'étude, mais indique plutôt les endroits où l'espèce n'existerait pas.
En pratique, il est souvent difficile de collecter des données d'absence réelles. C'est pourquoi des données de pseudo-absence générées artificiellement sont fréquemment utilisées. Toutefois, il est important de reconnaître les limites et les erreurs potentielles de cette méthode, car les points de pseudo-absence générés artificiellement peuvent ne pas refléter avec précision les véritables zones d'absence.
Le choix entre ces deux méthodes dépend de la disponibilité des données, des objectifs de recherche, de la précision et de la fiabilité du modèle, ainsi que du temps et des ressources disponibles. Ici, nous utiliserons les données d'occurrence collectées auprès de GBIF et les données de pseudo-absence générées artificiellement pour la modélisation à l'aide de la méthode "Présence-Absence".
La génération de données de pseudo-absence sera effectuée à l'aide de l'approche de profilage environnemental. Voici les étapes spécifiques :
Classification environnementale à l'aide du clustering en k-moyennes : l'algorithme de clustering en k-moyennes, basé sur la distance euclidienne, sera utilisé pour diviser les pixels de la zone d'étude en deux clusters. Un cluster représentera les zones présentant des caractéristiques environnementales similaires à celles de 100 lieux de présence sélectionnés au hasard, tandis que l'autre cluster représentera les zones présentant des caractéristiques différentes.
Génération de données de pseudo-absence dans des clusters dissemblables : dans le deuxième cluster identifié à la première étape (qui présente des caractéristiques environnementales différentes de celles des données de présence), des points de pseudo-absence générés de manière aléatoire seront créés. Ces points de pseudo-absence représenteront les zones où l'espèce n'est pas censée exister.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Ajustement et prédiction du modèle
Nous allons maintenant diviser les données en données d'entraînement et données de test. Les données d'entraînement seront utilisées pour trouver les paramètres optimaux en entraînant le modèle, tandis que les données de test serviront à évaluer le modèle entraîné au préalable. Dans ce contexte, l'autocorrélation spatiale est un concept important à prendre en compte.
L'autocorrélation spatiale est un élément essentiel de la modélisation de la distribution des espèces (SDM), associé à la loi de Tobler. Il incarne le concept selon lequel "tout est lié à tout, mais les choses proches sont plus liées que les choses éloignées". L'autocorrélation spatiale représente la relation significative entre l'emplacement des espèces et les variables environnementales. Toutefois, si une autocorrélation spatiale existe entre les données d'entraînement et de test, l'indépendance entre les deux ensembles de données peut être compromise. Cela a un impact significatif sur l'évaluation de la capacité de généralisation du modèle.
Une méthode pour résoudre ce problème consiste à utiliser la technique de validation croisée par blocs spatiaux, qui consiste à diviser les données en ensembles de données d'entraînement et de test. Cette technique consiste à diviser les données en plusieurs blocs, en utilisant chaque bloc indépendamment comme ensemble de données d'entraînement et de test pour réduire l'impact de l'autocorrélation spatiale. Cela renforce l'indépendance entre les ensembles de données, ce qui permet d'évaluer plus précisément la capacité de généralisation du modèle.
Voici la procédure spécifique à suivre :
- Création de blocs spatiaux : divisez l'ensemble de données en blocs spatiaux de taille égale (par exemple, 50 x 50 km).
- Attribution des ensembles d'entraînement et de test : chaque bloc spatial est attribué de manière aléatoire à l'ensemble d'entraînement (70 %) ou à l'ensemble de test (30 %). Cela empêche le modèle de surapprendre les données provenant de zones spécifiques et vise à obtenir des résultats plus généralisés.
- Validation croisée itérative : l'ensemble du processus est répété n fois (par exemple, 10 fois). À chaque itération, les blocs sont à nouveau divisés de manière aléatoire en ensembles d'entraînement et de test, ce qui vise à améliorer la stabilité et la fiabilité du modèle.
- Génération de données de pseudo-absence : à chaque itération, des données de pseudo-absence sont générées de manière aléatoire pour évaluer les performances du modèle.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Nous pouvons maintenant ajuster le modèle. L'ajustement d'un modèle implique de comprendre les tendances des données et d'ajuster les paramètres du modèle (poids et biais) en conséquence. Ce processus permet au modèle de faire des prédictions plus précises lorsqu'il est confronté à de nouvelles données. Pour ce faire, nous avons défini une fonction appelée SDM() pour ajuster le modèle.
Nous allons utiliser l'algorithme Random Forest.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
Les blocs spatiaux sont divisés en deux : 70 % pour l'entraînement du modèle et 30 % pour le test du modèle. Les données de pseudo-absence sont générées de manière aléatoire dans chaque ensemble d'entraînement et de test à chaque itération. Par conséquent, chaque exécution génère différents ensembles de données de présence et de pseudo-absence pour l'entraînement et le test du modèle.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Nous pouvons maintenant visualiser la carte de l'adéquation de l'habitat et la carte de la distribution potentielle pour la pitta féerique. Dans ce cas, la carte de l'adéquation de l'habitat est créée à l'aide de la fonction mean() pour calculer la moyenne de chaque emplacement de pixel sur toutes les images. La carte de la distribution potentielle est générée à l'aide de la fonction mode() pour déterminer la valeur la plus fréquente à chaque emplacement de pixel sur toutes les images.

# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Importance des variables et évaluation de la précision
La forêt aléatoire (ee.Classifier.smileRandomForest) est l'une des méthodes d'apprentissage par ensemble. Elle fonctionne en construisant plusieurs arbres de décision pour faire des prédictions. Chaque arbre de décision apprend indépendamment à partir de différents sous-ensembles de données, et leurs résultats sont agrégés pour permettre des prédictions plus précises et stables.
L'importance des variables est une mesure qui évalue l'impact de chaque variable sur les prédictions dans le modèle de forêt aléatoire. Nous allons utiliser importances_list défini précédemment pour calculer et imprimer l'importance moyenne des variables.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
À l'aide des ensembles de données de test, nous calculons l'AUC-ROC et l'AUC-PR pour chaque exécution. Nous calculons ensuite l'AUC-ROC et l'AUC-PR moyennes sur n itérations.
L'AUC-ROC représente l'aire sous la courbe du graphique "Sensibilité (rappel) vs 1-spécificité", qui illustre la relation entre la sensibilité et la spécificité lorsque le seuil change. La spécificité est basée sur toutes les non-occurrences observées. Par conséquent, l'AUC-ROC englobe tous les quadrants de la matrice de confusion.
AUC-PR représente l'aire sous la courbe du graphique "Précision vs rappel (sensibilité)", qui montre la relation entre la précision et le rappel lorsque le seuil varie. La précision est basée sur toutes les occurrences prédites. Par conséquent, l'AUC-PR n'inclut pas les vrais négatifs (VN).
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
Ce tutoriel a fourni un exemple pratique d'utilisation de Google Earth Engine (GEE) pour la modélisation de la distribution des espèces (SDM). Un point important à retenir est la polyvalence et la flexibilité de GEE dans le domaine de la gestion des données spatiales. Les puissantes capacités de traitement des données géospatiales d'Earth Engine offrent aux chercheurs et aux défenseurs de l'environnement des possibilités infinies pour comprendre et préserver la biodiversité de notre planète. En appliquant les connaissances et les compétences acquises dans ce tutoriel, les utilisateurs peuvent explorer ce domaine fascinant de la recherche écologique et y contribuer.
 Exécuter dans Google Colab
Exécuter dans Google Colab
 Afficher la source sur GitHub
Afficher la source sur GitHub