W tym samouczku przedstawimy metodologię modelowania rozmieszczenia gatunków za pomocą Google Earth Engine. Najpierw przedstawimy krótki przegląd modelowania rozmieszczenia gatunków, a następnie proces prognozowania i analizowania siedlisk zagrożonego gatunku ptaka, jakim jest pitta wróżkowa (nazwa naukowa: Pitta nympha).
Uruchom mnie jako pierwszego
Aby zainicjować interfejs API, uruchom tę komórkę. Wynik będzie zawierać instrukcje, jak przyznać temu notatnikowi dostęp do Earth Engine za pomocą Twojego konta.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Krótkie omówienie modelowania rozmieszczenia gatunków
Przyjrzyjmy się modelom rozmieszczenia gatunków, zaletom korzystania z Google Earth Engine do ich przetwarzania, danym wymaganym przez te modele oraz strukturze przepływu pracy.
Czym jest modelowanie rozmieszczenia gatunków?
Modelowanie rozmieszczenia gatunków (SDM) to najpopularniejsza metoda szacowania rzeczywistego lub potencjalnego rozmieszczenia geograficznego gatunku. Polega na określeniu warunków środowiskowych odpowiednich dla danego gatunku, a następnie na ustaleniu, gdzie te odpowiednie warunki występują geograficznie.
W ostatnich latach modelowanie rozmieszczenia gatunków stało się kluczowym elementem planowania ochrony przyrody. W tym celu opracowano różne techniki modelowania. Wdrożenie SDM w Google Earth Engine (GEE) zapewnia łatwy dostęp do danych środowiskowych na dużą skalę, a także do zaawansowanych możliwości obliczeniowych i obsługi algorytmów uczenia maszynowego, co umożliwia szybkie modelowanie.
Dane wymagane w SDM
SDM zwykle wykorzystuje relację między znanymi rekordami występowania gatunków a zmiennymi środowiskowymi, aby określić warunki, w których populacja może się utrzymać. Innymi słowy, wymagane są 2 typy danych wejściowych modelu:
- Rekordy występowania znanych gatunków
- Różne zmienne środowiskowe
Dane te są wprowadzane do algorytmów, aby określić warunki środowiskowe związane z występowaniem gatunków.
Przepływ pracy SDM z wykorzystaniem GEE
Przepływ pracy w przypadku SDM z użyciem GEE wygląda tak:
- Zbieranie i wstępne przetwarzanie danych o występowaniu gatunków
- Definicja obszaru zainteresowań
- Dodawanie zmiennych środowiskowych GEE
- Generowanie danych o pseudo-nieobecności
- Dopasowywanie modelu i prognozowanie
- Ocena ważności i dokładności zmiennych
Prognozowanie i analiza siedlisk za pomocą GEE
Krasnosójka (Pitta nympha) posłuży jako studium przypadku, aby zademonstrować zastosowanie modelu SDM opartego na GEE. W tym przykładzie wybrano konkretny gatunek, ale badacze mogą zastosować tę metodę do dowolnego interesującego ich gatunku docelowego, wprowadzając niewielkie modyfikacje w podanym kodzie źródłowym.
Krasnosójka wróżkowa to rzadki letni migrant i ptak przelotny w Korei Południowej, którego obszar występowania powiększa się ze względu na niedawne ocieplenie klimatu na Półwyspie Koreańskim. Jest to gatunek rzadki, zagrożony wyginięciem (klasa II), pomnik przyrody nr 204, oceniany jako regionalnie wymarły (RE) na krajowej czerwonej liście oraz jako narażony (VU) według kategorii IUCN.
Przeprowadzanie modelowania rozmieszczenia gatunków w celu planowania ochrony wróżki niebieskiej wydaje się bardzo przydatne. Teraz przejdźmy do prognozowania i analizy siedlisk za pomocą GEE.
Najpierw importowane są biblioteki Pythona.Instrukcja import wczytuje całą zawartość modułu, a instrukcja from import umożliwia importowanie określonych obiektów z modułu.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Zbieranie i wstępne przetwarzanie danych o występowaniu gatunków
Teraz zbierzmy dane o występowaniu wróżki. Nawet jeśli nie masz obecnie dostępu do danych o występowaniu interesującego Cię gatunku, możesz uzyskać dane obserwacyjne dotyczące konkretnych gatunków za pomocą interfejsu GBIF API. Interfejs GBIF API to interfejs, który umożliwia dostęp do danych o rozmieszczeniu gatunków udostępnianych przez GBIF. Użytkownicy mogą wyszukiwać, filtrować i pobierać dane, a także uzyskiwać różne informacje o gatunkach.
W poniższym kodzie zmiennej species_name przypisana jest nazwa naukowa gatunku (np. Pitta nympha w przypadku pitty wróżkowej), a zmiennej country_code przypisany jest kod kraju (np. KR w przypadku Korei Południowej). Zmienna base_url przechowuje adres interfejsu GBIF API. params to słownik zawierający parametry, które mają być użyte w żądaniu do interfejsu API:
scientificName: Ustawia nazwę naukową gatunku, który ma być wyszukiwany.country: ogranicza wyszukiwanie do określonego kraju.hasCoordinate: zapewnia, że wyszukiwane są tylko dane ze współrzędnymi (prawda).basisOfRecord: Wybiera tylko rekordy obserwacji dokonanych przez ludzi (HUMAN_OBSERVATION).limit: ustawia maksymalną liczbę zwracanych wyników na 10 000.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
Korzystając z wcześniej ustawionych parametrów, wysyłamy do interfejsu GBIF API zapytanie o rekordy obserwacji krasnoliczka wróżkowego (Pitta nympha) i wczytujemy wyniki do obiektu DataFrame, aby sprawdzić pierwszy wiersz. DataFrame to struktura danych do obsługi danych w formacie tabeli, składająca się z wierszy i kolumn. W razie potrzeby ramkę danych można zapisać jako plik CSV i ponownie odczytać.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
Następnie przekształcamy strukturę DataFrame w strukturę GeoDataFrame, która zawiera kolumnę z informacjami geograficznymi (geometry), i sprawdzamy pierwszy wiersz. Obiekt GeoDataFrame można zapisać jako plik GeoPackage (*.gpkg) i odczytać z powrotem.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Tym razem utworzyliśmy funkcję wizualizacji rozkładu danych według roku i miesiąca z obiektu GeoDataFrame i wyświetlania ich w postaci wykresu, który można następnie zapisać jako plik obrazu. Korzystanie z mapy cieplnej pozwala nam szybko zrozumieć częstotliwość występowania gatunków w poszczególnych latach i miesiącach, co zapewnia intuicyjną wizualizację zmian i wzorców czasowych w danych. Umożliwia to identyfikację wzorców czasowych i sezonowych w danych o występowaniu gatunków, a także szybkie wykrywanie wartości odstających lub problemów z jakością danych.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
Dane z 1995 roku są bardzo rzadkie i mają znaczne luki w porównaniu z innymi latami. Miesiące sierpień i wrzesień również mają ograniczone próbki i wykazują inne cechy sezonowe w porównaniu z innymi okresami. Wykluczenie tych danych może przyczynić się do zwiększenia stabilności i możliwości prognozowania modelu.
Pamiętaj jednak, że wykluczenie danych może zwiększyć zdolność modelu do generalizacji, ale może też prowadzić do utraty cennych informacji istotnych z punktu widzenia celów badania. Dlatego takie decyzje należy podejmować po dokładnym rozważeniu wszystkich okoliczności.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Teraz przefiltrowany obiekt GeoDataFrame jest konwertowany na obiekt Google Earth Engine.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
Następnie określimy rozmiar piksela rastrowego wyników SDM jako rozdzielczość 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Jeśli w tym samym rastrowym pikselu o rozdzielczości 1 km znajduje się wiele punktów występowania, istnieje duże prawdopodobieństwo, że w tej samej lokalizacji geograficznej panują te same warunki środowiskowe. Bezpośrednie użycie takich danych w analizie może spowodować zniekształcenie wyników.
Innymi słowy, musimy ograniczyć potencjalny wpływ błędu próbkowania geograficznego. W tym celu zachowamy tylko jedną lokalizację w każdym pikselu o wymiarach 1 km i usuniemy wszystkie pozostałe, co pozwoli modelowi bardziej obiektywnie odzwierciedlać warunki środowiskowe.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
Poniżej znajduje się wizualizacja porównująca geograficzne odchylenie próbkowania przed przetwarzaniem wstępnym (na niebiesko) i po nim (na czerwono). Aby ułatwić porównanie, mapa została wyśrodkowana na obszar o wysokim stężeniu współrzędnych występowania krasnoliczka w Parku Narodowym Hallasan.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Definicja obszaru zainteresowań
Określenie obszaru zainteresowania (AOI) to termin używany przez badaczy na oznaczenie obszaru geograficznego, który chcą analizować. Ma podobne znaczenie do terminu obszar badań.
W tym kontekście uzyskaliśmy pole ograniczające geometrii warstwy punktu występowania i utworzyliśmy wokół niego bufor o promieniu 50 km (z maksymalną tolerancją 1000 m), aby zdefiniować obszar zainteresowania.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
Dodawanie zmiennych środowiskowych GEE
Teraz dodajmy do analizy zmienne środowiskowe. GEE udostępnia szeroki zakres zbiorów danych dotyczących zmiennych środowiskowych, takich jak temperatura, opady, wysokość nad poziomem morza, pokrycie terenu i teren. Te zbiory danych umożliwiają nam kompleksową analizę różnych czynników, które mogą wpływać na preferencje siedliskowe tego gatunku.
Wybór zmiennych środowiskowych GEE w SDM powinien odzwierciedlać charakterystykę preferencji siedliskowych gatunku. W tym celu należy przeprowadzić wcześniejsze badania i przegląd literatury dotyczącej preferencji siedliskowych tego gatunku. Ten samouczek koncentruje się na przepływie pracy SDM z użyciem GEE, więc niektóre szczegółowe informacje zostały pominięte.
WorldClim V1 Bioclim: ten zbiór danych zawiera 19 zmiennych bioklimatycznych pochodzących z miesięcznych danych o temperaturze i opadach. Obejmuje okres od 1960 r. do 1991 r. i ma rozdzielczość 927,67 m.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m: ten zbiór danych zawiera cyfrowe dane o wysokości pochodzące z misji Shuttle Radar Topography Mission (SRTM). Dane zostały zebrane głównie około 2000 roku i mają rozdzielczość około 30 metrów (1 sekunda łuku). Poniższy kod oblicza warstwy wysokości, nachylenia, ekspozycji i cieniowania na podstawie danych SRTM.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: zbiór danych Vegetation Continuous Fields (VCF) z satelity Landsat szacuje odsetek pionowo rzutowanej pokrywy roślinnej, gdy wysokość roślinności przekracza 5 metrów. Ten zbiór danych jest dostępny dla 4 okresów, których środki przypadają na lata 2000, 2005, 2010 i 2015, a jego rozdzielczość wynosi 30 metrów. Używane są tu wartości mediany z tych 4 okresów.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (zmienne bioklimatyczne), terrain (topografia) i median_tcc (pokrywa koron drzew) są łączone w jeden obraz wielopasmowy. Pasmo elevation jest wybierane z pasma terrain, a w przypadku lokalizacji, w których elevation jest większe niż 0, tworzone jest pasmo watermask. Maskuje to obszary poniżej poziomu morza (np. oceany) i przygotowuje badacza do kompleksowej analizy różnych czynników środowiskowych w przypadku AOI.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Gdy w modelu uwzględnione są zmienne predykcyjne o wysokiej korelacji, mogą wystąpić problemy z wielokolinearnością. Współliniowość to zjawisko, które występuje, gdy w modelu występują silne zależności liniowe między zmiennymi niezależnymi, co prowadzi do niestabilności w szacowaniu współczynników (wag) modelu. Ta niestabilność może zmniejszyć wiarygodność modelu i utrudnić prognozowanie lub interpretowanie nowych danych. Dlatego weźmiemy pod uwagę współliniowość i przejdziemy do procesu wyboru zmiennych predykcyjnych.
Najpierw wygenerujemy 5000 losowych punktów, a następnie wyodrębnimy w tych punktach wartości zmiennych predykcyjnych z pojedynczego obrazu wielopasmowego.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Wyodrębnione wartości predyktorów dla każdego punktu przekonwertujemy na ramkę danych, a następnie sprawdzimy pierwszy wiersz.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Obliczanie współczynników korelacji Spearmana między podanymi zmiennymi predykcyjnymi i wyświetlanie ich na mapie cieplnej.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
Współczynnik korelacji Spearmana jest przydatny do zrozumienia ogólnych powiązań między zmiennymi predykcyjnymi, ale nie ocenia bezpośrednio interakcji między wieloma zmiennymi, w szczególności nie wykrywa współliniowości.
Współczynnik inflacji wariancji (VIF) to miara statystyczna służąca do oceny współliniowości i wyboru zmiennych. Wskazuje stopień liniowej zależności każdej zmiennej niezależnej od innych zmiennych niezależnych, a wysokie wartości VIF mogą świadczyć o współliniowości.
Zwykle, gdy wartości VIF przekraczają 5 lub 10, oznacza to, że zmienna jest silnie skorelowana z innymi zmiennymi, co może zagrażać stabilności i interpretowalności modelu. W tym samouczku do wyboru zmiennych użyto kryterium wartości VIF mniejszych niż 10. Na podstawie współczynnika VIF wybrano te 6 zmiennych.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
Następnie zwizualizujmy na mapie 6 wybranych zmiennych predykcyjnych.
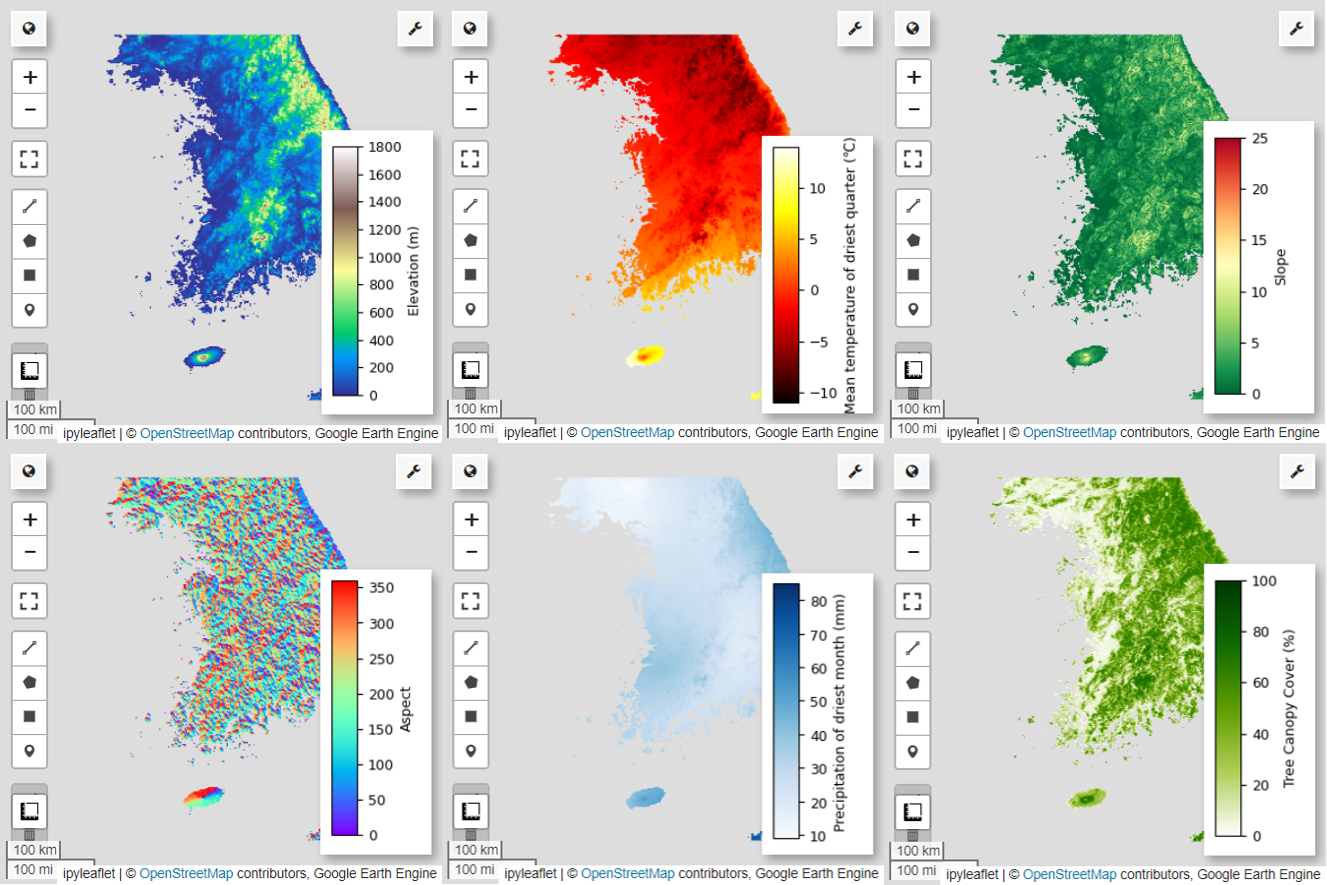
Dostępne palety do wizualizacji mapy możesz sprawdzić za pomocą tego kodu. Na przykład paleta terrain wygląda tak:cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Generowanie danych o pseudo-nieobecności
W procesie modelowania rozmieszczenia gatunków wybór danych wejściowych dla danego gatunku odbywa się głównie za pomocą 2 metod:
Metoda obecności i tła: ta metoda porównuje lokalizacje, w których zaobserwowano dany gatunek (obecność), z innymi lokalizacjami, w których go nie zaobserwowano (tło). Dane w tle nie muszą oznaczać obszarów, na których dany gatunek nie występuje, ale raczej odzwierciedlają ogólne warunki środowiskowe obszaru badań. Służy do odróżniania odpowiednich środowisk, w których gatunek może występować, od mniej odpowiednich.
Metoda obecności i nieobecności: ta metoda porównuje lokalizacje, w których gatunek został zaobserwowany (obecność), z lokalizacjami, w których na pewno nie został zaobserwowany (nieobecność). Dane o nieobecności reprezentują konkretne lokalizacje, w których dany gatunek nie występuje. Nie odzwierciedla ogólnych warunków środowiskowych na obszarze badań, ale wskazuje lokalizacje, w których gatunek prawdopodobnie nie występuje.
W praktyce często trudno jest zebrać prawdziwe dane o nieobecności, dlatego często używa się sztucznie generowanych danych o pseudo-nieobecności. Należy jednak pamiętać o ograniczeniach i potencjalnych błędach tej metody, ponieważ wygenerowane sztucznie punkty pseudo-nieobecności mogą nie odzwierciedlać dokładnie obszarów rzeczywistej nieobecności.
Wybór między tymi 2 metodami zależy od dostępności danych, celów badania, dokładności i wiarygodności modelu, a także czasu i zasobów. W tym przypadku użyjemy danych o występowaniu zebranych z GBIF i sztucznie wygenerowanych danych o pseudo-nieobecności, aby modelować za pomocą metody „Obecność–nieobecność”.
Generowanie danych o pseudo-nieobecności będzie odbywać się za pomocą „metody profilowania środowiskowego”. Poszczególne kroki są następujące:
Klasyfikacja środowiskowa za pomocą klastrowania k-średnich: algorytm klastrowy k-średnich oparty na odległości euklidesowej zostanie użyty do podzielenia pikseli na obszarze badań na 2 klastry. Jeden klaster będzie reprezentować obszary o podobnych cechach środowiskowych do losowo wybranych 100 lokalizacji występowania, a drugi – obszary o innych cechach.
Generowanie danych o pseudo-nieobecności w obrębie niepodobnych klastrów: w obrębie drugiego klastra zidentyfikowanego w pierwszym kroku (który ma inne cechy środowiskowe niż dane o obecności) zostaną utworzone losowo wygenerowane punkty pseudo-nieobecności. Te punkty pseudo-nieobecności będą reprezentować lokalizacje, w których nie oczekuje się występowania danego gatunku.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Dopasowywanie modelu i prognozowanie
Teraz podzielimy dane na dane treningowe i dane testowe. Dane treningowe posłużą do znalezienia optymalnych parametrów przez wytrenowanie modelu, a dane testowe – do oceny wcześniej wytrenowanego modelu. Ważną koncepcją w tym kontekście jest autokorelacja przestrzenna.
Autokorelacja przestrzenna to istotny element SDM związany z prawem Toblera. Opiera się na koncepcji, że „wszystko jest ze sobą powiązane, ale rzeczy bliskie są bardziej powiązane niż rzeczy odległe”. Autokorelacja przestrzenna odzwierciedla istotną zależność między lokalizacją gatunków a zmiennymi środowiskowymi. Jeśli jednak między danymi treningowymi a danymi testowymi występuje autokorelacja przestrzenna, niezależność tych dwóch zbiorów danych może zostać naruszona. Ma to znaczący wpływ na ocenę zdolności modelu do uogólniania.
Jedną z metod rozwiązania tego problemu jest technika przestrzennej blokowej walidacji krzyżowej, która polega na podzieleniu danych na zbiory do trenowania i testowania. Ta technika polega na podzieleniu danych na kilka bloków i użyciu każdego z nich niezależnie jako zbioru danych do trenowania i testowania, aby zmniejszyć wpływ autokorelacji przestrzennej. Zwiększa to niezależność zbiorów danych, co pozwala dokładniej ocenić zdolność modelu do generalizacji.
Konkretna procedura wygląda następująco:
- Tworzenie bloków przestrzennych: podziel cały zbiór danych na bloki przestrzenne o równej wielkości (np. 50 x 50 km).
- Przypisanie zbiorów treningowych i testowych: każdy blok przestrzenny jest losowo przypisywany do zbioru treningowego (70%) lub testowego (30%). Zapobiega to nadmiernemu dopasowaniu modelu do danych z określonych obszarów i pozwala uzyskać bardziej uogólnione wyniki.
- Iteracyjna walidacja krzyżowa: cały proces jest powtarzany n razy (np. 10 razy). W każdej iteracji bloki są ponownie losowo dzielone na zbiory treningowe i testowe, co ma na celu zwiększenie stabilności i niezawodności modelu.
- Generowanie danych o pseudonieobecności: w każdej iteracji dane o pseudonieobecności są generowane losowo w celu oceny wydajności modelu.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Teraz możemy dopasować model. Dopasowywanie modelu polega na rozpoznawaniu wzorców w danych i odpowiednim dostosowywaniu parametrów modelu (wag i odchyleń). Dzięki temu model może dokładniej prognozować na podstawie nowych danych. W tym celu zdefiniowaliśmy funkcję SDM(), aby dopasować model.
Użyjemy algorytmu Random Forest.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
Bloki przestrzenne są podzielone w proporcjach 70% do trenowania modelu i 30% do jego testowania. Dane o pseudonieobecności są losowo generowane w każdym zbiorze treningowym i testowym w każdej iteracji. W rezultacie każde wykonanie daje różne zbiory danych o obecności i pseudo-nieobecności do trenowania i testowania modelu.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Teraz możemy wizualizować mapę odpowiedniości siedlisk i mapę potencjalnego rozmieszczenia dla pitki tęczowej. W tym przypadku mapa przydatności siedliska jest tworzona za pomocą funkcji mean(), która oblicza średnią dla każdego piksela we wszystkich obrazach, a potencjalna mapa rozmieszczenia jest generowana za pomocą funkcji mode(), która określa najczęściej występującą wartość w każdym pikselu we wszystkich obrazach.
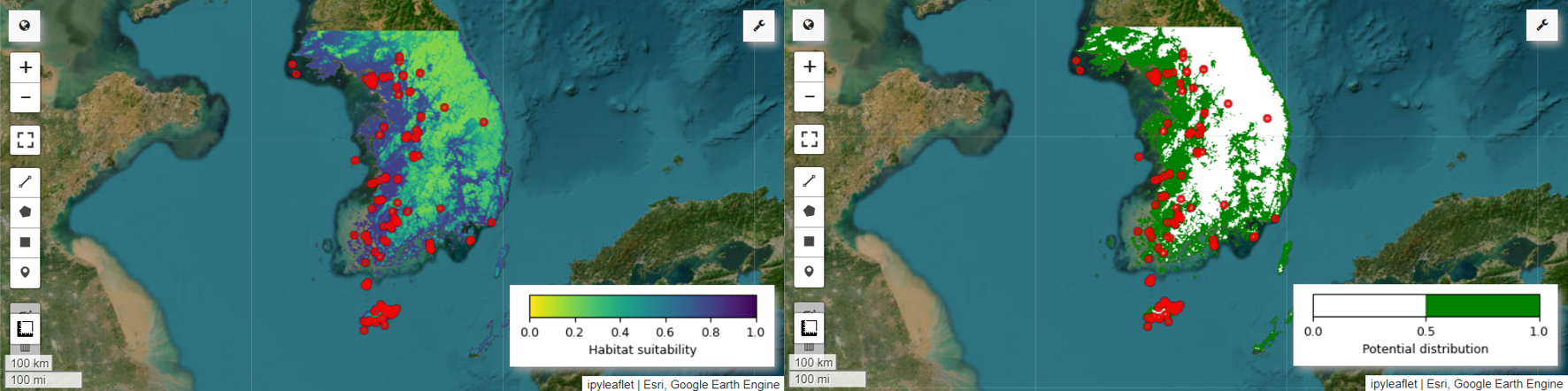
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Ocena ważności i dokładności zmiennych
Random Forest (ee.Classifier.smileRandomForest) to jedna z metod uczenia zespołowego, która działa poprzez tworzenie wielu drzew decyzyjnych w celu dokonywania prognoz. Każde drzewo decyzyjne uczy się niezależnie na podstawie różnych podzbiorów danych, a jego wyniki są agregowane, aby umożliwić dokładniejsze i stabilniejsze prognozy.
Znaczenie zmiennej to miara, która ocenia wpływ każdej zmiennej na prognozy w modelu lasu losowego. Do obliczenia i wydrukowania średniej ważności zmiennej użyjemy wcześniej zdefiniowanego symbolu importances_list.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
Korzystając ze zbiorów danych testowych, obliczamy AUC-ROC i AUC-PR dla każdego uruchomienia. Następnie obliczamy średnie wartości AUC-ROC i AUC-PR w n iteracjach.
AUC-ROC to obszar pod krzywą na wykresie „Czułość (odwołanie) a 1 – specyficzność”, który ilustruje zależność między czułością a specyficznością w miarę zmiany progu. Specyficzność jest określana na podstawie wszystkich zaobserwowanych przypadków braku wystąpienia. Dlatego AUC-ROC obejmuje wszystkie ćwiartki macierzy pomyłek.
AUC-PR to obszar pod krzywą na wykresie „Precyzja a czułość”, który pokazuje zależność między precyzją a czułością przy różnych progach. Precyzja jest obliczana na podstawie wszystkich przewidywanych wystąpień. Dlatego AUC-PR nie uwzględnia wyników prawdziwie negatywnych (TN).
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
W tym samouczku przedstawiliśmy praktyczny przykład wykorzystania Google Earth Engine (GEE) do modelowania rozmieszczenia gatunków (SDM). Ważnym wnioskiem jest wszechstronność i elastyczność GEE w dziedzinie modelowania dystrybucji gatunków. Wykorzystanie zaawansowanych możliwości przetwarzania danych geoprzestrzennych Earth Engine otwiera przed badaczami i ekologami nieograniczone możliwości poznawania i ochrony bioróżnorodności naszej planety. Dzięki wiedzy i umiejętnościom zdobytym w tym samouczku możesz odkrywać tę fascynującą dziedzinę badań ekologicznych i w niej uczestniczyć.
 Uruchom w Google Colab
Uruchom w Google Colab
 Wyświetl źródło w GitHubie
Wyświetl źródło w GitHubie