In dieser Anleitung wird die Methodik der Modellierung der Artenverteilung mit Google Earth Engine vorgestellt. Es wird ein kurzer Überblick über die Modellierung der Artenverteilung gegeben, gefolgt vom Prozess der Vorhersage und Analyse des Lebensraums einer gefährdeten Vogelart, die als Feenpitta (wissenschaftlicher Name: Pitta nympha) bekannt ist.
Zuerst ausführen
Führen Sie die folgende Zelle aus, um die API zu initialisieren. Die Ausgabe enthält eine Anleitung dazu, wie Sie diesem Notebook mit Ihrem Konto Zugriff auf Earth Engine gewähren.
import ee
# Trigger the authentication flow.
ee.Authenticate()
# Initialize the library.
ee.Initialize(project='my-project')
Kurzer Überblick über die Modellierung der Artenverteilung
Wir sehen uns an, was Artenverteilungsmodelle sind, welche Vorteile die Verwendung von Google Earth Engine für die Verarbeitung bietet, welche Daten für die Modelle erforderlich sind und wie der Workflow strukturiert ist.
Was ist die Modellierung der Artenverteilung?
Die Modellierung der Artenverteilung (Species Distribution Modeling, SDM) ist die gängigste Methode zur Schätzung der tatsächlichen oder potenziellen geografischen Verteilung einer Art. Dabei werden die für eine bestimmte Art geeigneten Umweltbedingungen charakterisiert und dann ermittelt, wo diese geeigneten Bedingungen geografisch verteilt sind.
SDM hat sich in den letzten Jahren zu einem wichtigen Bestandteil der Naturschutzplanung entwickelt, und es wurden verschiedene Modellierungstechniken für diesen Zweck entwickelt. Die Implementierung von SDM in Google Earth Engine (GEE) bietet einfachen Zugriff auf groß angelegte Umweltdaten sowie leistungsstarke Rechenfunktionen und Unterstützung für Algorithmen für maschinelles Lernen, was eine schnelle Modellierung ermöglicht.
Für SDM erforderliche Daten
Bei SDM wird in der Regel die Beziehung zwischen bekannten Aufzeichnungen zum Vorkommen von Arten und Umweltvariablen verwendet, um die Bedingungen zu ermitteln, unter denen eine Population überleben kann. Mit anderen Worten: Es sind zwei Arten von Modelleingabedaten erforderlich:
- Vorkommensdatensätze bekannter Arten
- Verschiedene Umgebungsvariablen
Diese Daten werden in Algorithmen eingegeben, um Umweltbedingungen zu ermitteln, die mit dem Vorhandensein von Arten in Verbindung stehen.
Workflow von SDM mit GEE
Der Workflow für SDM mit GEE sieht so aus:
- Erhebung und Vorverarbeitung von Daten zum Vorkommen von Arten
- Definition der interessierenden Region
- GEE-Umgebungsvariablen hinzufügen
- Generierung von Pseudo-Abwesenheitsdaten
- Modellanpassung und ‑vorhersage
- Variablenwichtigkeit und Genauigkeitsbewertung
Habitat Prediction and Analysis Using GEE
Die Nymphenpitta (Pitta nympha) wird als Fallstudie verwendet, um die Anwendung von GEE-basierten SDMs zu demonstrieren. Obwohl diese spezielle Art für ein Beispiel ausgewählt wurde, können Forscher die Methode mit geringfügigen Änderungen am bereitgestellten Quellcode auf jede gewünschte Zielart anwenden.
Die Feenpitta ist ein seltener Sommer- und Durchzügler in Südkorea, dessen Verbreitungsgebiet sich aufgrund der jüngsten Klimaerwärmung auf der koreanischen Halbinsel ausdehnt. Sie wird als seltene Art, gefährdete Wildtiere der Klasse II, Naturdenkmal Nr. 204, in der Nationalen Roten Liste als „Regional ausgestorben“ (RE) und nach den IUCN-Kategorien als „Gefährdet“ (VU) eingestuft.
Die Durchführung von SDM für die Naturschutzplanung der Feenpitta scheint sehr wertvoll zu sein. Sehen wir uns nun die Vorhersage und Analyse von Lebensräumen mit GEE an.
Zuerst werden die Python-Bibliotheken importiert.Mit der Anweisung import wird der gesamte Inhalt eines Moduls importiert, während mit der Anweisung from import bestimmte Objekte aus einem Modul importiert werden können.
# Import libraries
import geemap
import geemap.colormaps as cm
import pandas as pd, geopandas as gpd
import numpy as np, matplotlib.pyplot as plt
import os, requests, math, random
from ipyleaflet import TileLayer
from statsmodels.stats.outliers_influence import variance_inflation_factor
Erhebung und Vorverarbeitung von Daten zum Vorkommen von Arten
Als Nächstes erfassen wir Daten zum Vorkommen des Feenpittas. Auch wenn Sie derzeit keinen Zugriff auf Daten zum Vorkommen der gewünschten Art haben, können Sie über die GBIF-API Beobachtungsdaten zu bestimmten Arten abrufen. Die GBIF-API ist eine Schnittstelle, die den Zugriff auf die von GBIF bereitgestellten Daten zur Verbreitung von Arten ermöglicht. Nutzer können damit Daten suchen, filtern und herunterladen sowie verschiedene Informationen zu Arten abrufen.
Im Code unten wird der Variablen species_name der wissenschaftliche Name der Art zugewiesen (z.B. Pitta nympha für Feenpitta) und der Variablen country_code wird der Ländercode zugewiesen (z.B. KR für Südkorea). In der Variablen base_url wird die Adresse der GBIF API gespeichert. params ist ein Dictionary mit Parametern, die in der API-Anfrage verwendet werden sollen:
scientificName: Legt den wissenschaftlichen Namen der zu suchenden Art fest.country: Schränkt die Suche auf ein bestimmtes Land ein.hasCoordinate: Sorgt dafür, dass nur Daten mit Koordinaten (wahr) durchsucht werden.basisOfRecord: Wählt nur Datensätze mit menschlicher Beobachtung (HUMAN_OBSERVATION) aus.limit: Legt die maximale Anzahl der zurückgegebenen Ergebnisse auf 10.000 fest.
def get_gbif_species_data(species_name, country_code):
"""
Retrieves observational data for a specific species using the GBIF API and returns it as a pandas DataFrame.
Parameters:
species_name (str): The scientific name of the species to query.
country_code (str): The country code of the where the observation data will be queried.
Returns:
pd.DataFrame: A pandas DataFrame containing the observational data.
"""
base_url = "https://api.gbif.org/v1/occurrence/search"
params = {
"scientificName": species_name,
"country": country_code,
"hasCoordinate": "true",
"basisOfRecord": "HUMAN_OBSERVATION",
"limit": 10000,
}
try:
response = requests.get(base_url, params=params)
response.raise_for_status() # Raises an exception for a response error.
data = response.json()
occurrences = data.get("results", [])
if occurrences: # If data is present
df = pd.json_normalize(occurrences)
return df
else:
print("No data found for the given species and country code.")
return pd.DataFrame() # Returns an empty DataFrame
except requests.RequestException as e:
print(f"Request failed: {e}")
return pd.DataFrame() # Returns an empty DataFrame in case of an exception
Mit den zuvor festgelegten Parametern fragen wir die GBIF API nach Beobachtungsdatensätzen der Feenpitta (Pitta nympha) ab und laden die Ergebnisse in einen DataFrame, um die erste Zeile zu prüfen. Ein DataFrame ist eine Datenstruktur zum Verarbeiten von tabellarischen Daten, die aus Zeilen und Spalten besteht. Bei Bedarf kann der DataFrame als CSV-Datei gespeichert und wieder eingelesen werden.
# Retrieve Fairy Pitta data
df = get_gbif_species_data("Pitta nympha", "KR")
"""
# Save DataFrame to CSV and read back in.
df.to_csv("pitta_nympha_data.csv", index=False)
df = pd.read_csv("pitta_nympha_data.csv")
"""
df.head(1) # Display the first row of the DataFrame
Als Nächstes wandeln wir den DataFrame in einen GeoDataFrame um, der eine Spalte für geografische Informationen (geometry) enthält, und prüfen die erste Zeile. Ein GeoDataFrame kann als GeoPackage-Datei (*.gpkg) gespeichert und wieder eingelesen werden.
# Convert DataFrame to GeoDataFrame
gdf = gpd.GeoDataFrame(
df,
geometry=gpd.points_from_xy(df.decimalLongitude,
df.decimalLatitude),
crs="EPSG:4326"
)[["species", "year", "month", "geometry"]]
"""
# Convert GeoDataFrame to GeoPackage (requires pycrs module)
%pip install -U -q pycrs
gdf.to_file("pitta_nympha_data.gpkg", driver="GPKG")
gdf = gpd.read_file("pitta_nympha_data.gpkg")
"""
gdf.head(1) # Display the first row of the GeoDataFrame
Dieses Mal haben wir eine Funktion erstellt, mit der die Verteilung der Daten nach Jahr und Monat aus dem GeoDataFrame visualisiert und als Diagramm dargestellt werden kann. Das Diagramm kann dann als Bilddatei gespeichert werden. Mithilfe einer Heatmap können wir die Häufigkeit des Vorkommens von Arten nach Jahr und Monat schnell erfassen und so eine intuitive Visualisierung der zeitlichen Änderungen und Muster in den Daten erhalten. So lassen sich zeitliche Muster und saisonale Schwankungen in den Daten zum Vorkommen von Arten erkennen und Ausreißer oder Qualitätsprobleme in den Daten schnell erkennen.
# Yearly and monthly data distribution heatmap
def plot_heatmap(gdf, h_size=8):
statistics = gdf.groupby(["month", "year"]).size().unstack(fill_value=0)
# Heatmap
plt.figure(figsize=(h_size, h_size - 6))
heatmap = plt.imshow(
statistics.values, cmap="YlOrBr", origin="upper", aspect="auto"
)
# Display values above each pixel
for i in range(len(statistics.index)):
for j in range(len(statistics.columns)):
plt.text(
j, i, statistics.values[i, j], ha="center", va="center", color="black"
)
plt.colorbar(heatmap, label="Count")
plt.title("Monthly Species Count by Year")
plt.xlabel("Year")
plt.ylabel("Month")
plt.xticks(range(len(statistics.columns)), statistics.columns)
plt.yticks(range(len(statistics.index)), statistics.index)
plt.tight_layout()
plt.savefig("heatmap_plot.png")
plt.show()
plot_heatmap(gdf)
Die Daten von 1995 sind sehr spärlich und weisen im Vergleich zu anderen Jahren erhebliche Lücken auf. Auch für die Monate August und September sind nur begrenzte Stichproben verfügbar und sie weisen im Vergleich zu anderen Zeiträumen unterschiedliche saisonale Merkmale auf. Wenn Sie diese Daten ausschließen, kann das dazu beitragen, die Stabilität und Vorhersagekraft des Modells zu verbessern.
Es ist jedoch wichtig zu beachten, dass das Ausschließen von Daten die Generalisierungsfähigkeit des Modells verbessern kann, aber auch zum Verlust wertvoller Informationen führen kann, die für die Forschungsziele relevant sind. Solche Entscheidungen sollten daher sorgfältig getroffen werden.
# Filtering data by year and month
filtered_gdf = gdf[
(~gdf['year'].eq(1995)) &
(~gdf['month'].between(8, 9))
]
Der gefilterte GeoDataFrame wird jetzt in ein Google Earth Engine-Objekt konvertiert.
# Convert GeoDataFrame to Earth Engine object
data_raw = geemap.geopandas_to_ee(filtered_gdf)
Als Nächstes definieren wir die Rasterpixelgröße der SDM-Ergebnisse als 1 km.
# Spatial resolution setting (meters)
grain_size = 1000
Wenn mehrere Fundorte im selben Rasterpixel mit einer Auflösung von 1 km vorhanden sind, ist es sehr wahrscheinlich, dass sie am selben geografischen Standort dieselben Umweltbedingungen aufweisen. Wenn Sie solche Daten direkt in die Analyse einbeziehen, können die Ergebnisse verfälscht werden.
Mit anderen Worten: Wir müssen die potenziellen Auswirkungen von geografischen Stichprobenerhebungs-Bias begrenzen. Dazu behalten wir nur einen Standort innerhalb jedes 1‑km-Pixels bei und entfernen alle anderen, damit das Modell die Umweltbedingungen objektiver widerspiegeln kann.
def remove_duplicates(data, grain_size):
# Select one occurrence record per pixel at the chosen spatial resolution
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
rand_point_vals = random_raster.sampleRegions(
collection=ee.FeatureCollection(data), geometries=True
)
return rand_point_vals.distinct("random")
data = remove_duplicates(data_raw, grain_size)
# Before selection and after selection
print("Original data size:", data_raw.size().getInfo())
print("Final data size:", data.size().getInfo())
Unten sehen Sie eine Visualisierung, in der der geografische Stichprobeneffekt vor (blau) und nach (rot) der Vorverarbeitung verglichen wird. Um den Vergleich zu erleichtern, wurde die Karte auf das Gebiet mit einer hohen Konzentration von Koordinaten für das Vorkommen von Feenpittas im Hallasan-Nationalpark zentriert.
# Visualization of geographic sampling bias before (blue) and after (red) preprocessing
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
# Add the random raster layer
random_raster = ee.Image.random().reproject("EPSG:4326", None, grain_size)
Map.addLayer(
random_raster,
{"min": 0, "max": 1, "palette": ["black", "white"], "opacity": 0.5},
"Random Raster",
)
# Add the original data layer in blue
Map.addLayer(data_raw, {"color": "blue"}, "Original data")
# Add the final data layer in red
Map.addLayer(data, {"color": "red"}, "Final data")
# Set the center of the map to the coordinates
Map.setCenter(126.712, 33.516, 14)
Map
Definition der interessierenden Region
Die Definition des Untersuchungsgebiets (Area of Interest, AOI) bezieht sich auf den Begriff, den Forscher verwenden, um das geografische Gebiet zu bezeichnen, das sie analysieren möchten. Er hat eine ähnliche Bedeutung wie der Begriff „Untersuchungsgebiet“.
In diesem Zusammenhang haben wir die Bounding Box der Geometrie der Ebene mit den Fundorten abgerufen und einen 50 km-Puffer darum erstellt (mit einer maximalen Toleranz von 1.000 Metern), um das AOI zu definieren.
# Define the AOI
aoi = data.geometry().bounds().buffer(distance=50000, maxError=1000)
# Add the AOI to the map
outline = ee.Image().byte().paint(
featureCollection=aoi, color=1, width=3)
Map.remove_layer("Random Raster")
Map.addLayer(outline, {'palette': 'FF0000'}, "AOI")
Map.centerObject(aoi, 6)
Map
GEE-Umgebungsvariablen hinzufügen
Fügen wir der Analyse nun Umgebungsvariablen hinzu. GEE bietet eine Vielzahl von Datasets für Umgebungsvariablen wie Temperatur, Niederschlag, Höhe, Bodenbedeckung und Gelände. Mithilfe dieser Datasets können wir verschiedene Faktoren umfassend analysieren, die die Lebensraumpräferenzen der Feenpitta beeinflussen können.
Die Auswahl der GEE-Umgebungsvariablen im SDM sollte die Habitatpräferenzen der Art widerspiegeln. Dazu sollten vorab Studien und eine Literaturrecherche zu den Lebensraumpräferenzen der Feenpitta durchgeführt werden. In dieser Anleitung geht es hauptsächlich um den Workflow von SDM mit GEE. Daher werden einige detaillierte Informationen ausgelassen.
WorldClim V1 Bioclim: Dieser Datensatz enthält 19 bioklimatische Variablen, die aus monatlichen Temperatur- und Niederschlagsdaten abgeleitet wurden. Sie deckt den Zeitraum von 1960 bis 1991 ab und hat eine Auflösung von 927,67 Metern.
# WorldClim V1 Bioclim
bio = ee.Image("WORLDCLIM/V1/BIO")
NASA SRTM Digital Elevation 30m: Dieser Datensatz enthält digitale Höhendaten aus der Shuttle Radar Topography Mission (SRTM). Die Daten wurden hauptsächlich um das Jahr 2000 erhoben und haben eine Auflösung von etwa 30 Metern (1 Bogensekunde). Mit dem folgenden Code werden die Ebenen für Höhe, Neigung, Ausrichtung und Schummerung aus den SRTM-Daten berechnet.
# NASA SRTM Digital Elevation 30m
terrain = ee.Algorithms.Terrain(ee.Image("USGS/SRTMGL1_003"))
Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m: Das VCF-Dataset (Vegetation Continuous Fields) von Landsat schätzt den Anteil der vertikal projizierten Vegetationsbedeckung, wenn die Vegetationshöhe mehr als 5 Meter beträgt. Dieser Datensatz ist für vier Zeiträume um die Jahre 2000, 2005, 2010 und 2015 mit einer Auflösung von 30 Metern verfügbar. Hier werden die Medianwerte aus diesen vier Zeiträumen verwendet.
# Global Forest Cover Change (GFCC) Tree Cover Multi-Year Global 30m
tcc = ee.ImageCollection("NASA/MEASURES/GFCC/TC/v3")
median_tcc = (
tcc.filterDate("2000-01-01", "2015-12-31")
.select(["tree_canopy_cover"], ["TCC"])
.median()
)
bio (bioklimatische Variablen), terrain (Topografie) und median_tcc (Baumkronenbedeckung) werden zu einem einzelnen Multibandbild kombiniert. Das Band elevation wird aus terrain ausgewählt und für Standorte, an denen elevation größer als 0 ist, wird ein watermask erstellt. Dadurch werden Regionen unter dem Meeresspiegel (z.B. der Ozean) maskiert und der Forscher kann verschiedene Umweltfaktoren für das AOI umfassend analysieren.
# Combine bands into a multi-band image
predictors = bio.addBands(terrain).addBands(median_tcc)
# Create a water mask
watermask = terrain.select('elevation').gt(0)
# Mask out ocean pixels and clip to the area of interest
predictors = predictors.updateMask(watermask).clip(aoi)
Wenn stark korrelierte Vorhersagevariablen gemeinsam in ein Modell aufgenommen werden, können Probleme mit Multikollinearität auftreten. Multikollinearität ist ein Phänomen, das auftritt, wenn es starke lineare Beziehungen zwischen unabhängigen Variablen in einem Modell gibt. Dies führt zu Instabilität bei der Schätzung der Koeffizienten (Gewichtungen) des Modells. Diese Instabilität kann die Zuverlässigkeit des Modells verringern und Vorhersagen oder Interpretationen für neue Daten erschweren. Daher berücksichtigen wir die Multikollinearität und fahren mit der Auswahl der Vorhersagevariablen fort.
Zuerst werden 5.000 zufällige Punkte generiert und dann die Werte der Vorhersagevariablen des einzelnen Multibandbilds an diesen Punkten extrahiert.
# Generate 5,000 random points
data_cor = predictors.sample(scale=grain_size, numPixels=5000, geometries=True)
# Extract predictor variable values
pvals = predictors.sampleRegions(collection=data_cor, scale=grain_size)
Wir wandeln die extrahierten Vorhersagewerte für jeden Punkt in einen DataFrame um und prüfen dann die erste Zeile.
# Converting predictor values from Earth Engine to a DataFrame
pvals_df = geemap.ee_to_df(pvals)
pvals_df.head(1)
# Displaying the columns
columns = pvals_df.columns
print(columns)
Berechnung von Spearman-Korrelationskoeffizienten zwischen den angegebenen Vorhersagevariablen und Visualisierung in einer Heatmap.
def plot_correlation_heatmap(dataframe, h_size=10, show_labels=False):
# Calculate Spearman correlation coefficients
correlation_matrix = dataframe.corr(method="spearman")
# Create a heatmap
plt.figure(figsize=(h_size, h_size-2))
plt.imshow(correlation_matrix, cmap='coolwarm', interpolation='nearest')
# Optionally display values on the heatmap
if show_labels:
for i in range(correlation_matrix.shape[0]):
for j in range(correlation_matrix.shape[1]):
plt.text(j, i, f"{correlation_matrix.iloc[i, j]:.2f}",
ha='center', va='center', color='white', fontsize=8)
columns = dataframe.columns.tolist()
plt.xticks(range(len(columns)), columns, rotation=90)
plt.yticks(range(len(columns)), columns)
plt.title("Variables Correlation Matrix")
plt.colorbar(label="Spearman Correlation")
plt.savefig('correlation_heatmap_plot.png')
plt.show()
# Plot the correlation heatmap of variables
plot_correlation_heatmap(pvals_df)
Der Spearman-Korrelationskoeffizient ist nützlich, um die allgemeinen Beziehungen zwischen Vorhersagevariablen zu verstehen, bewertet aber nicht direkt, wie mehrere Variablen interagieren, insbesondere um Multikollinearität zu erkennen.
Der Varianzinflationsfaktor (VIF) ist ein statistischer Messwert, mit dem Multikollinearität bewertet und die Variablenauswahl gesteuert wird. Er gibt den Grad der linearen Beziehung jeder unabhängigen Variablen zu den anderen unabhängigen Variablen an. Hohe VIF-Werte können ein Hinweis auf Multikollinearität sein.
Wenn VIF-Werte 5 oder 10 überschreiten, deutet das in der Regel darauf hin, dass die Variable stark mit anderen Variablen korreliert. Das kann die Stabilität und Interpretierbarkeit des Modells beeinträchtigen. In dieser Anleitung wurde für die Variablenauswahl ein Kriterium von VIF-Werten unter 10 verwendet. Die folgenden sechs Variablen wurden auf Grundlage des VIF ausgewählt.
# Filter variables based on Variance Inflation Factor (VIF)
def filter_variables_by_vif(dataframe, threshold=10):
original_columns = dataframe.columns.tolist()
remaining_columns = original_columns[:]
while True:
vif_data = dataframe[remaining_columns]
vif_values = [
variance_inflation_factor(vif_data.values, i)
for i in range(vif_data.shape[1])
]
max_vif_index = vif_values.index(max(vif_values))
max_vif = max(vif_values)
if max_vif < threshold:
break
print(f"Removing '{remaining_columns[max_vif_index]}' with VIF {max_vif:.2f}")
del remaining_columns[max_vif_index]
filtered_data = dataframe[remaining_columns]
bands = filtered_data.columns.tolist()
print("Bands:", bands)
return filtered_data, bands
filtered_pvals_df, bands = filter_variables_by_vif(pvals_df)
# Variable Selection Based on VIF
predictors = predictors.select(bands)
# Plot the correlation heatmap of variables
plot_correlation_heatmap(filtered_pvals_df, h_size=6, show_labels=True)
Als Nächstes visualisieren wir die sechs ausgewählten Vorhersagevariablen auf der Karte.
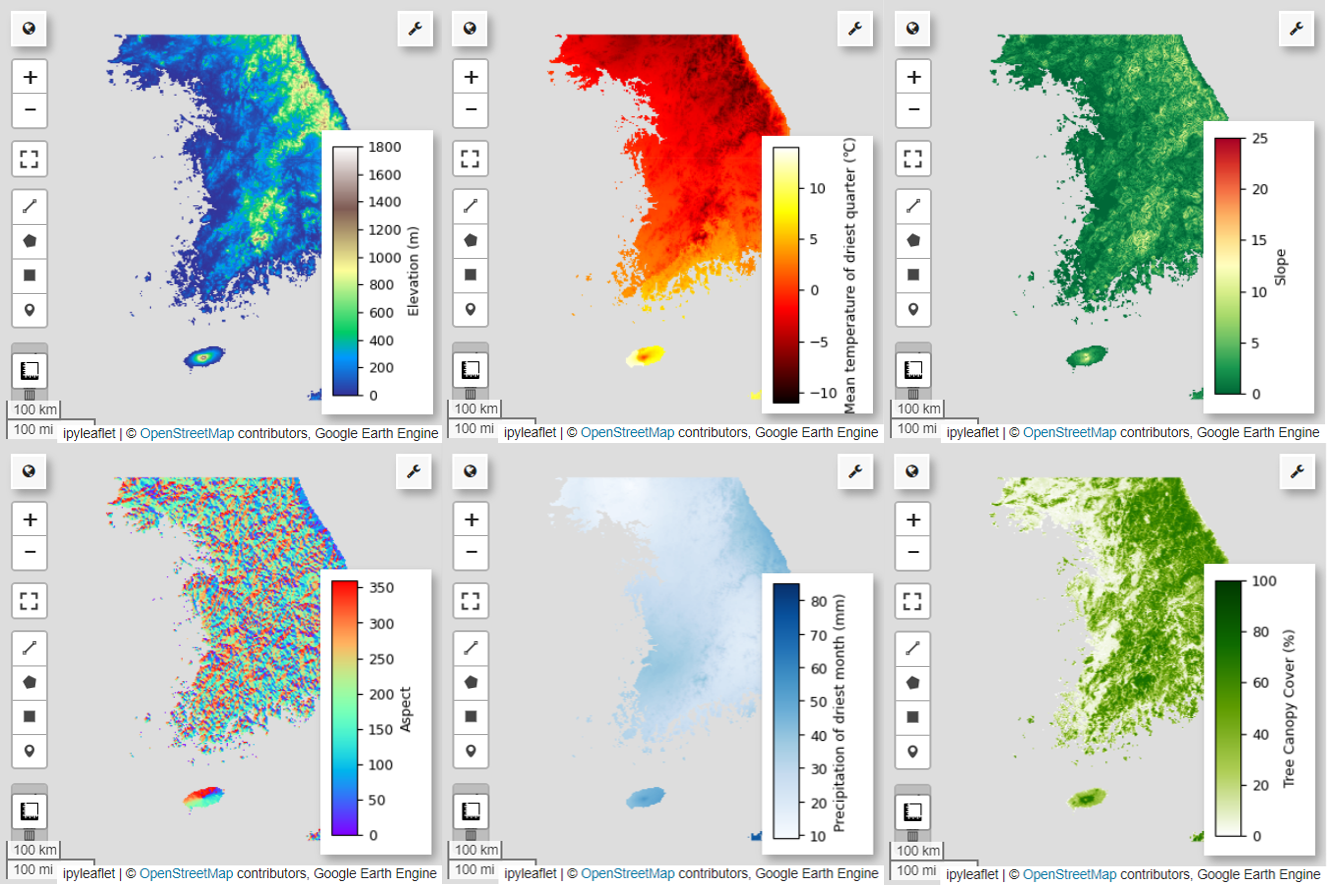
Mit dem folgenden Code können Sie die verfügbaren Paletten für die Kartendarstellung untersuchen. Die terrain-Palette sieht beispielsweise so aus.
cm.plot_colormaps(width=8.0, height=0.2)
cm.plot_colormap('terrain', width=8.0, height=0.2, orientation='horizontal')
# Elevation layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['elevation'], 'min': 0, 'max': 1800, 'palette': cm.palettes.terrain}
Map.addLayer(predictors, vis_params, 'elevation')
Map.add_colorbar(vis_params, label="Elevation (m)", orientation="vertical", layer_name="elevation")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio09
min_max_val = (
predictors.select("bio09")
.multiply(0.1)
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio09 (Mean temperature of driest quarter) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"min": math.floor(min_max_val["bio09_min"]),
"max": math.ceil(min_max_val["bio09_max"]),
"palette": cm.palettes.hot,
}
Map.addLayer(predictors.select("bio09").multiply(0.1), vis_params, "bio09")
Map.add_colorbar(
vis_params,
label="Mean temperature of driest quarter (℃)",
orientation="vertical",
layer_name="bio09",
)
Map.centerObject(aoi, 6)
Map
# Slope layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['slope'], 'min': 0, 'max': 25, 'palette': cm.palettes.RdYlGn_r}
Map.addLayer(predictors, vis_params, 'slope')
Map.add_colorbar(vis_params, label="Slope", orientation="vertical", layer_name="slope")
Map.centerObject(aoi, 6)
Map
# Aspect layer
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
vis_params = {'bands':['aspect'], 'min': 0, 'max': 360, 'palette': cm.palettes.rainbow}
Map.addLayer(predictors, vis_params, 'aspect')
Map.add_colorbar(vis_params, label="Aspect", orientation="vertical", layer_name="aspect")
Map.centerObject(aoi, 6)
Map
# Calculate the minimum and maximum values for bio14
min_max_val = (
predictors.select("bio14")
.reduceRegion(reducer=ee.Reducer.minMax(), scale=1000)
.getInfo()
)
# bio14 (Precipitation of driest month) layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["bio14"],
"min": math.floor(min_max_val["bio14_min"]),
"max": math.ceil(min_max_val["bio14_max"]),
"palette": cm.palettes.Blues,
}
Map.addLayer(predictors, vis_params, "bio14")
Map.add_colorbar(
vis_params,
label="Precipitation of driest month (mm)",
orientation="vertical",
layer_name="bio14",
)
Map.centerObject(aoi, 6)
Map
# TCC layer
Map = geemap.Map(layout={"height": "400px", "width": "800px"})
vis_params = {
"bands": ["TCC"],
"min": 0,
"max": 100,
"palette": ["ffffff", "afce56", "5f9c00", "0e6a00", "003800"],
}
Map.addLayer(predictors, vis_params, "TCC")
Map.add_colorbar(
vis_params, label="Tree Canopy Cover (%)", orientation="vertical", layer_name="TCC"
)
Map.centerObject(aoi, 6)
Map
Generierung von Pseudo-Abwesenheitsdaten
Bei der SDM-Methode wird die Auswahl der Eingabedaten für eine Art hauptsächlich mit zwei Methoden angegangen:
Methode „Anwesenheit – Hintergrund“: Bei dieser Methode werden die Orte, an denen eine bestimmte Art beobachtet wurde (Anwesenheit), mit anderen Orten verglichen, an denen die Art nicht beobachtet wurde (Hintergrund). Die Hintergrunddaten beziehen sich hier nicht unbedingt auf Gebiete, in denen die Art nicht vorkommt, sondern sind so eingerichtet, dass sie die allgemeinen Umweltbedingungen des Untersuchungsgebiets widerspiegeln. Damit werden geeignete Umgebungen, in denen die Art vorkommen könnte, von weniger geeigneten unterschieden.
Methode zur Analyse von Anwesenheit und Abwesenheit: Bei dieser Methode werden Orte, an denen die Art beobachtet wurde (Anwesenheit), mit Orten verglichen, an denen sie definitiv nicht beobachtet wurde (Abwesenheit). Hier stehen Abwesenheitsdaten für bestimmte Orte, an denen die Art bekanntermaßen nicht vorkommt. Sie spiegelt nicht die allgemeinen Umweltbedingungen des Untersuchungsgebiets wider, sondern verweist auf Orte, an denen die Art voraussichtlich nicht vorkommt.
In der Praxis ist es oft schwierig, echte Abwesenheitsdaten zu erheben. Daher werden häufig künstlich generierte Pseudo-Abwesenheitsdaten verwendet. Es ist jedoch wichtig, die Einschränkungen und potenziellen Fehler dieser Methode zu berücksichtigen, da künstlich generierte Pseudo-Abwesenheitspunkte möglicherweise nicht die tatsächlichen Abwesenheitsbereiche widerspiegeln.
Die Wahl zwischen diesen beiden Methoden hängt von der Datenverfügbarkeit, den Forschungszielen, der Modellgenauigkeit und ‑zuverlässigkeit sowie von Zeit und Ressourcen ab. Hier verwenden wir Daten zum Vorkommen, die von GBIF erhoben wurden, und künstlich generierte Pseudo-Abwesenheitsdaten, um das Modell mit der Methode „Anwesenheit/Abwesenheit“ zu erstellen.
Die Generierung von Pseudo-Abwesenheitsdaten erfolgt über den „Environmental Profiling Approach“. Die einzelnen Schritte sind:
Umweltklassifizierung mit k-Means-Clustering: Der k-Means-Clustering-Algorithmus, der auf der euklidischen Distanz basiert, wird verwendet, um die Pixel im Untersuchungsgebiet in zwei Cluster zu unterteilen. Ein Cluster repräsentiert Gebiete mit ähnlichen Umweltmerkmalen wie die zufällig ausgewählten 100 Standorte, an denen Nutzer präsent waren, während der andere Cluster Gebiete mit unterschiedlichen Merkmalen repräsentiert.
Generierung von Pseudo-Abwesenheitsdaten in unähnlichen Clustern: Im zweiten Cluster, der im ersten Schritt identifiziert wurde (mit anderen Umgebungsmerkmalen als die Anwesenheitsdaten), werden zufällig generierte Pseudo-Abwesenheitspunkte erstellt. Diese Pseudo-Abwesenheitspunkte stellen Orte dar, an denen die Art voraussichtlich nicht vorkommt.
# Randomly select 100 locations for occurrence
pvals = predictors.sampleRegions(
collection=data.randomColumn().sort('random').limit(100),
properties=[],
scale=grain_size
)
# Perform k-means clustering
clusterer = ee.Clusterer.wekaKMeans(
nClusters=2,
distanceFunction="Euclidean"
).train(pvals)
cl_result = predictors.cluster(clusterer)
# Get cluster ID for locations similar to occurrence
cl_id = cl_result.sampleRegions(
collection=data.randomColumn().sort('random').limit(200),
properties=[],
scale=grain_size
)
# Define non-occurrence areas in dissimilar clusters
cl_id = ee.FeatureCollection(cl_id).reduceColumns(ee.Reducer.mode(),['cluster'])
cl_id = ee.Number(cl_id.get('mode')).subtract(1).abs()
cl_mask = cl_result.select(['cluster']).eq(cl_id)
# Presence location mask
presence_mask = data.reduceToImage(properties=['random'],
reducer=ee.Reducer.first()
).reproject('EPSG:4326', None,
grain_size).mask().neq(1).selfMask()
# Masking presence locations in non-occurrence areas and clipping to AOI
area_for_pa = presence_mask.updateMask(cl_mask).clip(aoi)
# Area for Pseudo-absence
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(area_for_pa, {'palette': 'black'}, 'AreaForPA')
Map.centerObject(aoi, 6)
Map
Modellanpassung und ‑vorhersage
Wir teilen die Daten jetzt in Trainings- und Testdaten auf. Die Trainingsdaten werden verwendet, um die optimalen Parameter durch Trainieren des Modells zu ermitteln, während die Testdaten verwendet werden, um das zuvor trainierte Modell zu bewerten. Ein wichtiges Konzept in diesem Zusammenhang ist die räumliche Autokorrelation.
Die räumliche Autokorrelation ist ein wesentliches Element in SDM, das mit dem Gesetz von Tobler zusammenhängt. Es verkörpert das Konzept, dass „alles mit allem zusammenhängt, aber nahe Dinge stärker zusammenhängen als entfernte Dinge“. Die räumliche Autokorrelation stellt die signifikante Beziehung zwischen dem Standort von Arten und Umweltvariablen dar. Wenn jedoch eine räumliche Autokorrelation zwischen den Trainings- und Testdaten besteht, kann die Unabhängigkeit zwischen den beiden Datasets beeinträchtigt werden. Dies hat erhebliche Auswirkungen auf die Bewertung der Generalisierungsfähigkeit des Modells.
Eine Methode, um dieses Problem zu beheben, ist die räumliche Block-Kreuzvalidierung, bei der die Daten in Trainings- und Test-Datasets aufgeteilt werden. Bei dieser Methode werden die Daten in mehrere Blöcke unterteilt. Jeder Block wird unabhängig als Trainings- und Test-Dataset verwendet, um die Auswirkungen der räumlichen Autokorrelation zu verringern. Dadurch wird die Unabhängigkeit zwischen Datasets erhöht, was eine genauere Bewertung der Generalisierungsfähigkeit des Modells ermöglicht.
So gehen Sie vor:
- Erstellung von räumlichen Blöcken: Teilen Sie das gesamte Dataset in räumliche Blöcke gleicher Größe auf (z.B. 50 × 50 km).
- Zuweisung von Trainings- und Test-Datasets: Jeder räumliche Block wird nach dem Zufallsprinzip entweder dem Trainings-Dataset (70%) oder dem Test-Dataset (30%) zugewiesen. Dadurch wird verhindert, dass das Modell Daten aus bestimmten Bereichen überanpasst, und es werden allgemeinere Ergebnisse erzielt.
- Iterative Kreuzvalidierung: Der gesamte Prozess wird n-mal wiederholt (z.B. 10-mal). In jeder Iteration werden die Blöcke wieder zufällig in Trainings- und Testsets unterteilt, um die Stabilität und Zuverlässigkeit des Modells zu verbessern.
- Generierung von Pseudo-Abwesenheitsdaten: In jeder Iteration werden zufällig Pseudo-Abwesenheitsdaten generiert, um die Leistung des Modells zu bewerten.
Scale = 50000
grid = watermask.reduceRegions(
collection=aoi.coveringGrid(scale=Scale, proj='EPSG:4326'),
reducer=ee.Reducer.mean()).filter(ee.Filter.neq('mean', None))
Map = geemap.Map(layout={'height':'400px', 'width':'800px'})
Map.addLayer(grid, {}, "Grid for spatial block cross validation")
Map.addLayer(outline, {'palette': 'FF0000'}, "Study Area")
Map.centerObject(aoi, 6)
Map
Jetzt können wir das Modell anpassen. Beim Anpassen eines Modells müssen die Muster in den Daten erkannt und die Parameter des Modells (Gewichte und Bias) entsprechend angepasst werden. So kann das Modell genauere Vorhersagen treffen, wenn es mit neuen Daten konfrontiert wird. Dazu haben wir eine Funktion namens SDM() definiert, um das Modell anzupassen.
Wir verwenden den Random Forest-Algorithmus.
def sdm(x):
seed = ee.Number(x)
# Random block division for training and validation
rand_blk = ee.FeatureCollection(grid).randomColumn(seed=seed).sort("random")
training_grid = rand_blk.filter(ee.Filter.lt("random", split)) # Grid for training
testing_grid = rand_blk.filter(ee.Filter.gte("random", split)) # Grid for testing
# Presence points
presence_points = ee.FeatureCollection(data)
presence_points = presence_points.map(lambda feature: feature.set("PresAbs", 1))
tr_presence_points = presence_points.filter(
ee.Filter.bounds(training_grid)
) # Presence points for training
te_presence_points = presence_points.filter(
ee.Filter.bounds(testing_grid)
) # Presence points for testing
# Pseudo-absence points for training
tr_pseudo_abs_points = area_for_pa.sample(
region=training_grid,
scale=grain_size,
numPixels=tr_presence_points.size().add(300),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for training
tr_pseudo_abs_points = (
tr_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(tr_presence_points.size()))
)
tr_pseudo_abs_points = tr_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
te_pseudo_abs_points = area_for_pa.sample(
region=testing_grid,
scale=grain_size,
numPixels=te_presence_points.size().add(100),
seed=seed,
geometries=True,
)
# Same number of pseudo-absence points as presence points for testing
te_pseudo_abs_points = (
te_pseudo_abs_points.randomColumn()
.sort("random")
.limit(ee.Number(te_presence_points.size()))
)
te_pseudo_abs_points = te_pseudo_abs_points.map(lambda feature: feature.set("PresAbs", 0))
# Merge training and pseudo-absence points
training_partition = tr_presence_points.merge(tr_pseudo_abs_points)
testing_partition = te_presence_points.merge(te_pseudo_abs_points)
# Extract predictor variable values at training points
train_pvals = predictors.sampleRegions(
collection=training_partition,
properties=["PresAbs"],
scale=grain_size,
geometries=True,
)
# Random Forest classifier
classifier = ee.Classifier.smileRandomForest(
numberOfTrees=500,
variablesPerSplit=None,
minLeafPopulation=10,
bagFraction=0.5,
maxNodes=None,
seed=seed,
)
# Presence probability: Habitat suitability map
classifier_pr = classifier.setOutputMode("PROBABILITY").train(
train_pvals, "PresAbs", bands
)
classified_img_pr = predictors.select(bands).classify(classifier_pr)
# Binary presence/absence map: Potential distribution map
classifier_bin = classifier.setOutputMode("CLASSIFICATION").train(
train_pvals, "PresAbs", bands
)
classified_img_bin = predictors.select(bands).classify(classifier_bin)
return [
classified_img_pr,
classified_img_bin,
training_partition,
testing_partition,
], classifier_pr
Die räumlichen Blöcke werden in 70% für das Modelltraining und 30% für das Testen des Modells unterteilt. Pseudo-Abwesenheitsdaten werden in jeder Iteration zufällig in jedem Trainings- und Testsatz generiert. Daher liefert jede Ausführung unterschiedliche Mengen an Daten zu Anwesenheit und Pseudo-Abwesenheit für das Training und Testen des Modells.
split = 0.7
numiter = 10
# Random Seed
runif = lambda length: [random.randint(1, 1000) for _ in range(length)]
items = runif(numiter)
# Fixed seed
# items = [287, 288, 553, 226, 151, 255, 902, 267, 419, 538]
results_list = [] # Initialize SDM results list
importances_list = [] # Initialize variable importance list
for item in items:
result, trained = sdm(item)
# Accumulate SDM results into the list
results_list.extend(result)
# Accumulate variable importance into the list
importance = ee.Dictionary(trained.explain()).get('importance')
importances_list.extend(importance.getInfo().items())
# Flatten the SDM results list
results = ee.List(results_list).flatten()
Jetzt können wir die Karte zur Eignung des Lebensraums und die Karte zur potenziellen Verbreitung für die Feenpitta visualisieren. In diesem Fall wird die Karte zur Eignung des Lebensraums erstellt, indem mit der Funktion mean() der Durchschnitt für jede Pixelposition über alle Bilder hinweg berechnet wird. Die Karte zur potenziellen Verbreitung wird generiert, indem mit der Funktion mode() der am häufigsten vorkommende Wert an jeder Pixelposition über alle Bilder hinweg ermittelt wird.
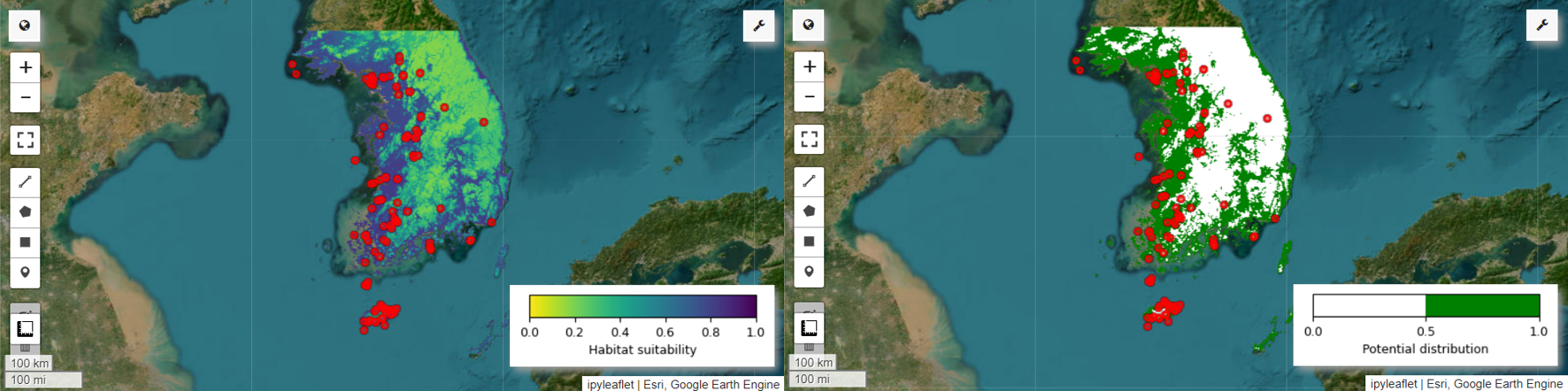
# Habitat suitability map
images = ee.List.sequence(
0, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x))
model_average = ee.ImageCollection.fromImages(images).mean()
Map = geemap.Map(layout={'height':'400px', 'width':'800px'}, basemap='Esri.WorldImagery')
vis_params = {
'min': 0,
'max': 1,
'palette': cm.palettes.viridis_r}
Map.addLayer(model_average, vis_params, 'Habitat suitability')
Map.add_colorbar(vis_params, label="Habitat suitability",
orientation="horizontal",
layer_name="Habitat suitability")
Map.addLayer(data, {'color':'red'}, 'Presence')
Map.centerObject(aoi, 6)
Map
# Potential distribution map
images2 = ee.List.sequence(1, ee.Number(numiter).multiply(4).subtract(1), 4).map(
lambda x: results.get(x)
)
distribution_map = ee.ImageCollection.fromImages(images2).mode()
Map = geemap.Map(
layout={"height": "400px", "width": "800px"}, basemap="Esri.WorldImagery"
)
vis_params = {"min": 0, "max": 1, "palette": ["white", "green"]}
Map.addLayer(distribution_map, vis_params, "Potential distribution")
Map.addLayer(data, {"color": "red"}, "Presence")
Map.add_colorbar(
vis_params,
label="Potential distribution",
discrete=True,
orientation="horizontal",
layer_name="Potential distribution",
)
Map.centerObject(data.geometry(), 6)
Map
Variablenwichtigkeit und Genauigkeitsbewertung
Random Forest (ee.Classifier.smileRandomForest) ist eine der Ensemble-Lernmethoden, bei der mehrere Entscheidungsbäume erstellt werden, um Vorhersagen zu treffen. Jeder Entscheidungsbaum lernt unabhängig von verschiedenen Teilmengen der Daten. Die Ergebnisse werden zusammengefasst, um genauere und stabilere Vorhersagen zu ermöglichen.
Die Variablenwichtigkeit ist ein Maß, mit dem die Auswirkungen der einzelnen Variablen auf die Vorhersagen im Random Forest-Modell bewertet werden. Wir verwenden die zuvor definierte importances_list, um die durchschnittliche Wichtigkeit der Variablen zu berechnen und auszugeben.
def plot_variable_importance(importances_list):
# Extract each variable importance value into a list
variables = [item[0] for item in importances_list]
importances = [item[1] for item in importances_list]
# Calculate the average importance for each variable
average_importances = {}
for variable in set(variables):
indices = [i for i, var in enumerate(variables) if var == variable]
average_importance = np.mean([importances[i] for i in indices])
average_importances[variable] = average_importance
# Sort the importances in descending order of importance
sorted_importances = sorted(average_importances.items(),
key=lambda x: x[1], reverse=False)
variables = [item[0] for item in sorted_importances]
avg_importances = [item[1] for item in sorted_importances]
# Adjust the graph size
plt.figure(figsize=(8, 4))
# Plot the average importance as a horizontal bar chart
plt.barh(variables, avg_importances)
plt.xlabel('Importance')
plt.ylabel('Variables')
plt.title('Average Variable Importance')
# Display values above the bars
for i, v in enumerate(avg_importances):
plt.text(v + 0.02, i, f"{v:.2f}", va='center')
# Adjust the x-axis range
plt.xlim(0, max(avg_importances) + 5) # Adjust to the desired range
plt.tight_layout()
plt.savefig('variable_importance.png')
plt.show()
plot_variable_importance(importances_list)
Anhand der Test-Datasets berechnen wir für jeden Lauf AUC-ROC und AUC-PR. Anschließend berechnen wir die durchschnittliche AUC-ROC und AUC-PR über n Iteration hinweg.
AUC-ROC steht für die Fläche unter der Kurve des Diagramms „Sensitivität (Trefferquote) im Vergleich zu 1 – Spezifität“. Sie veranschaulicht das Verhältnis zwischen Sensitivität und Spezifität bei Änderung des Grenzwerts. Die Spezifität basiert auf allen beobachteten Nicht-Ereignissen. Daher umfasst AUC-ROC alle Quadranten der Konfusionsmatrix.
AUC-PR steht für die Fläche unter der Kurve des Diagramms „Precision vs. Recall (Sensitivity)“ (Genauigkeit im Vergleich zur Trefferquote (Sensitivität)). Es zeigt das Verhältnis zwischen Genauigkeit und Trefferquote bei unterschiedlichen Schwellenwerten. Die Genauigkeit basiert auf allen vorhergesagten Ereignissen. Daher werden die echten Negativwerte (TN) nicht in die AUC-PR einbezogen.
def print_pres_abs_sizes(TestingDatasets, numiter):
# Check and print the sizes of presence and pseudo-absence coordinates
def get_pres_abs_size(x):
fc = ee.FeatureCollection(TestingDatasets.get(x))
presence_size = fc.filter(ee.Filter.eq("PresAbs", 1)).size()
pseudo_absence_size = fc.filter(ee.Filter.eq("PresAbs", 0)).size()
return ee.List([presence_size, pseudo_absence_size])
sizes_info = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(get_pres_abs_size)
.getInfo()
)
for i, sizes in enumerate(sizes_info):
presence_size = sizes[0]
pseudo_absence_size = sizes[1]
print(
f"Iteration {i + 1}: Presence Size = {presence_size}, Pseudo-absence Size = {pseudo_absence_size}"
)
# Extracting the Testing Datasets
testing_datasets = ee.List.sequence(
3, ee.Number(numiter).multiply(4).subtract(1), 4
).map(lambda x: results.get(x))
print_pres_abs_sizes(testing_datasets, numiter)
def get_acc(hsm, t_data, grain_size):
pr_prob_vals = hsm.sampleRegions(
collection=t_data, properties=["PresAbs"], scale=grain_size
)
seq = ee.List.sequence(start=0, end=1, count=25) # Divide 0 to 1 into 25 intervals
def calculate_metrics(cutoff):
# Each element of the seq list is passed as cutoff(threshold value)
# Observed present = TP + FN
pres = pr_prob_vals.filterMetadata("PresAbs", "equals", 1)
# TP (True Positive)
tp = ee.Number(
pres.filterMetadata("classification", "greater_than", cutoff).size()
)
# TPR (True Positive Rate) = Recall = Sensitivity = TP / (TP + FN) = TP / Observed present
tpr = tp.divide(pres.size())
# Observed absent = FP + TN
abs = pr_prob_vals.filterMetadata("PresAbs", "equals", 0)
# FN (False Negative)
fn = ee.Number(
pres.filterMetadata("classification", "less_than", cutoff).size()
)
# TNR (True Negative Rate) = Specificity = TN / (FP + TN) = TN / Observed absent
tn = ee.Number(abs.filterMetadata("classification", "less_than", cutoff).size())
tnr = tn.divide(abs.size())
# FP (False Positive)
fp = ee.Number(
abs.filterMetadata("classification", "greater_than", cutoff).size()
)
# FPR (False Positive Rate) = FP / (FP + TN) = FP / Observed absent
fpr = fp.divide(abs.size())
# Precision = TP / (TP + FP) = TP / Predicted present
precision = tp.divide(tp.add(fp))
# SUMSS = SUM of Sensitivity and Specificity
sumss = tpr.add(tnr)
return ee.Feature(
None,
{
"cutoff": cutoff,
"TP": tp,
"TN": tn,
"FP": fp,
"FN": fn,
"TPR": tpr,
"TNR": tnr,
"FPR": fpr,
"Precision": precision,
"SUMSS": sumss,
},
)
return ee.FeatureCollection(seq.map(calculate_metrics))
def calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter):
# Calculate AUC-ROC and AUC-PR
def calculate_auc_metrics(x):
hsm = ee.Image(images.get(x))
t_data = ee.FeatureCollection(testing_datasets.get(x))
acc = get_acc(hsm, t_data, grain_size)
# Calculate AUC-ROC
x = ee.Array(acc.aggregate_array("FPR"))
y = ee.Array(acc.aggregate_array("TPR"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_roc = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
# Calculate AUC-PR
x = ee.Array(acc.aggregate_array("TPR"))
y = ee.Array(acc.aggregate_array("Precision"))
x1 = x.slice(0, 1).subtract(x.slice(0, 0, -1))
y1 = y.slice(0, 1).add(y.slice(0, 0, -1))
auc_pr = x1.multiply(y1).multiply(0.5).reduce("sum", [0]).abs().toList().get(0)
return (auc_roc, auc_pr)
auc_metrics = (
ee.List.sequence(0, ee.Number(numiter).subtract(1), 1)
.map(calculate_auc_metrics)
.getInfo()
)
# Print AUC-ROC and AUC-PR for each iteration
df = pd.DataFrame(auc_metrics, columns=["AUC-ROC", "AUC-PR"])
df.index = [f"Iteration {i + 1}" for i in range(len(df))]
df.to_csv("auc_metrics.csv", index_label="Iteration")
print(df)
# Calculate mean and standard deviation of AUC-ROC and AUC-PR
mean_auc_roc, std_auc_roc = df["AUC-ROC"].mean(), df["AUC-ROC"].std()
mean_auc_pr, std_auc_pr = df["AUC-PR"].mean(), df["AUC-PR"].std()
print(f"Mean AUC-ROC = {mean_auc_roc:.4f} ± {std_auc_roc:.4f}")
print(f"Mean AUC-PR = {mean_auc_pr:.4f} ± {std_auc_pr:.4f}")
%%time
# Calculate AUC-ROC and AUC-PR
calculate_and_print_auc_metrics(images, testing_datasets, grain_size, numiter)
In dieser Anleitung wurde ein praktisches Beispiel für die Verwendung von Google Earth Engine (GEE) für die Modellierung der Artenverteilung (Species Distribution Modeling, SDM) vorgestellt. Eine wichtige Erkenntnis ist die Vielseitigkeit und Flexibilität von GEE im Bereich SDM. Die leistungsstarken Funktionen von Earth Engine zur Verarbeitung von Geodaten eröffnen Forschern und Naturschützern unzählige Möglichkeiten, die Artenvielfalt auf unserem Planeten zu verstehen und zu bewahren. Durch die Anwendung des in diesem Tutorial erworbenen Wissens und der erworbenen Fähigkeiten können Einzelpersonen dieses faszinierende Feld der ökologischen Forschung erkunden und dazu beitragen.
 In Google Colab ausführen
In Google Colab ausführen
 Quelle auf GitHub ansehen
Quelle auf GitHub ansehen