הפסד הוא מדד מספרי שמתאר עד כמה התחזיות של מודל שגויות. הפונקציה Loss מודדת את המרחק בין התחזיות של המודל לבין התוויות בפועל. המטרה של אימון מודל היא למזער את ההפסד, ולהקטין אותו לערך הנמוך ביותר האפשרי.
בתמונה הבאה אפשר לראות את ההפסד כחיצים שמצוירים מנקודות הנתונים אל המודל. החיצים מראים את המרחק בין התחזיות של המודל לבין הערכים בפועל.
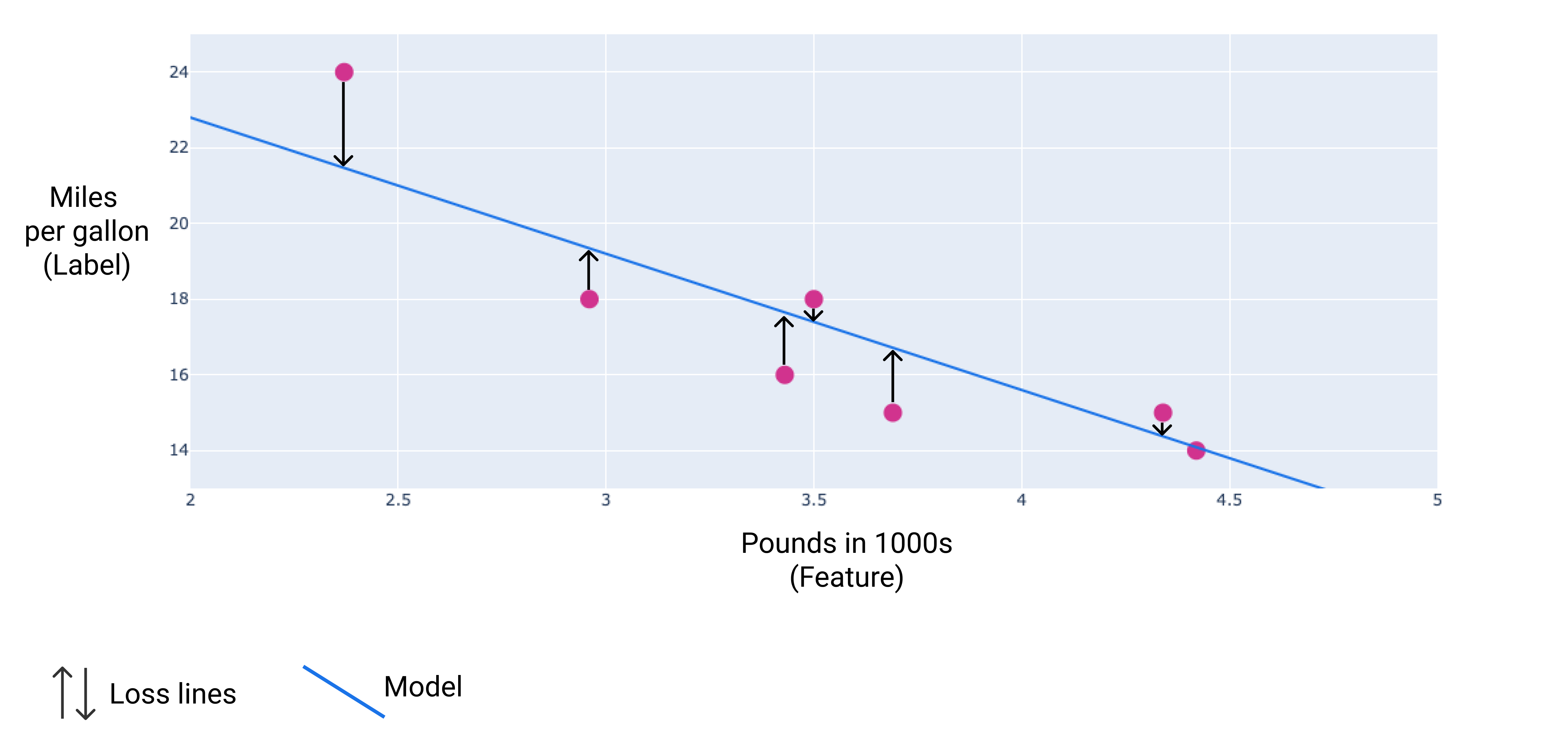
איור 8. ההפסד נמדד מהערך בפועל לערך החזוי.
מרחק ההפסד
בסטטיסטיקה ובלמידת מכונה, הפסד הוא מדד להפרש בין הערכים החזויים לבין הערכים בפועל. ההפסד מתמקד במרחק בין הערכים, ולא בכיוון. לדוגמה, אם מודל חוזה את הערך 2, אבל הערך בפועל הוא 5, לא משנה לנו שההפסד הוא שלילי (2-5=-3). מה שחשוב לנו הוא המרחק בין הערכים, שהוא 3. לכן, בכל השיטות לחישוב ההפסד, הסימן מוסר.
שתי השיטות הנפוצות ביותר להסרת הסימן הן:
- מחשבים את הערך המוחלט של ההפרש בין הערך בפועל לבין התחזית.
- מעלים בריבוע את ההפרש בין הערך בפועל לבין התחזית.
סוגי הפסדים
ברגרסיה ליניארית יש חמישה סוגים עיקריים של הפסדים, שמפורטים בטבלה הבאה.
| סוג האובדן | הגדרה | משוואה |
|---|---|---|
| הפסד L1 | סכום הערכים המוחלטים של ההפרש בין הערכים החזויים לבין הערכים בפועל. | $ ∑ | actual\ value - predicted\ value | $ |
| שגיאה ממוצעת מוחלטת (MAE) | הממוצע של הפסדי L1 על פני קבוצה של N דוגמאות. | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| L2 loss | סכום ההפרש בריבוע בין הערכים החזויים לבין הערכים בפועל. | $ ∑(actual\ value - predicted\ value)^2 $ |
| שגיאה ריבועית ממוצעת (MSE) | הממוצע של הפסדי L2 על פני קבוצה של N דוגמאות. | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| שורש טעות ריבועית ממוצעת (RMSE) | השורש הריבועי של השגיאה הריבועית הממוצעת (MSE). | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
ההבדל הפונקציונלי בין פונקציית אובדן L1 לבין פונקציית אובדן L2 (או בין MAE/RMSE לבין MSE) הוא העלאה בריבוע. כשההבדל בין התחזית לבין התווית גדול, העלאה בריבוע מגדילה עוד יותר את ההפסד. כשההבדל קטן (פחות מ-1), העלאה בריבוע מקטינה עוד יותר את ההפסד.
במקרים מסוימים, מדדי הפסד כמו MAE ו-RMSE עדיפים על הפסד L2 או MSE, כי בדרך כלל קל יותר להבין אותם. הם מודדים את השגיאה באמצעות אותו סולם שבו מודד המודל את הערך החזוי.
כשמעבדים כמה דוגמאות בבת אחת, מומלץ לחשב את הממוצע של ערכי השגיאה בכל הדוגמאות, בין אם משתמשים ב-MAE, ב-MSE או ב-RMSE.
דוגמה לחישוב הפסד
נשתמש בקו ההתאמה הטובה ביותר הקודם כדי לחשב את הפסד L2 עבור דוגמה אחת. מקו ההתאמה הטובה ביותר, קיבלנו את הערכים הבאים למשקל ולהטיה:
- $ \small{Weight: -4.6} $
- $ \small{Bias: 34} $
אם המודל חוזה שרכב במשקל 1,075 ק"ג צורך 9.8 ליטר ל-100 ק"מ, אבל בפועל הוא צורך 9 ליטר ל-100 ק"מ, נחשב את הפסד L2 באופן הבא:
| ערך | משוואה | תוצאה |
|---|---|---|
| חיזוי | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| ערך בפועל | $ \small{ label } $ | $ \small{ 26 } $ |
| הפסד L2 | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
בדוגמה הזו, הפסד L2 לנקודת הנתונים היחידה הזו הוא 8.41.
בחירת הפסד
ההחלטה אם להשתמש ב-MAE או ב-MSE יכולה להיות תלויה במערך הנתונים ובאופן שבו רוצים לטפל בתחזיות מסוימות. בדרך כלל, רוב ערכי התכונות במערך נתונים נמצאים בטווח מובחן. לדוגמה, מכוניות שוקלות בדרך כלל בין 900 ל-2,250 ק"ג וצריכת הדלק שלהן היא בין 3.4 ל-21.3 ק"מ לליטר. מכונית במשקל 3,600 ק"ג או מכונית שצורכת גלון דלק לכל 100 מיילים חורגת מהטווח האופייני ותיחשב חריגה.
מונח זה יכול גם להתייחס למרחק בין התחזיות של מודל לבין הערכים האמיתיים. לדוגמה, 3,000 פאונד נמצאים בטווח המשקל האופייני של מכונית, ו-40 מייל לגלון נמצאים בטווח צריכת הדלק האופיינית. עם זאת, רכב במשקל 1,360 ק"ג שצורך 17 ליטר לכל 100 ק"מ יהיה חריג בחיזוי של המודל, כי המודל יחזה שרכב במשקל 1,360 ק"ג יצרוך בערך 8.5 ליטר לכל 100 ק"מ.
כשבוחרים את פונקציית ההפסד הכי טובה, צריך לחשוב איך רוצים שהמודל יתייחס לערכים חריגים. לדוגמה, MSE מזיז את המודל יותר לכיוון הערכים החריגים, בעוד ש-MAE לא עושה זאת. הפסד של L2 גורר קנס גבוה הרבה יותר עבור חריג מאשר הפסד של L1. לדוגמה, בתמונות הבאות מוצג מודל שאומן באמצעות MAE ומודל שאומן באמצעות MSE. הקו האדום מייצג מודל שעבר אימון מלא וישמש ליצירת תחזיות. הערכים החריגים קרובים יותר למודל שאומן באמצעות MSE מאשר למודל שאומן באמצעות MAE.
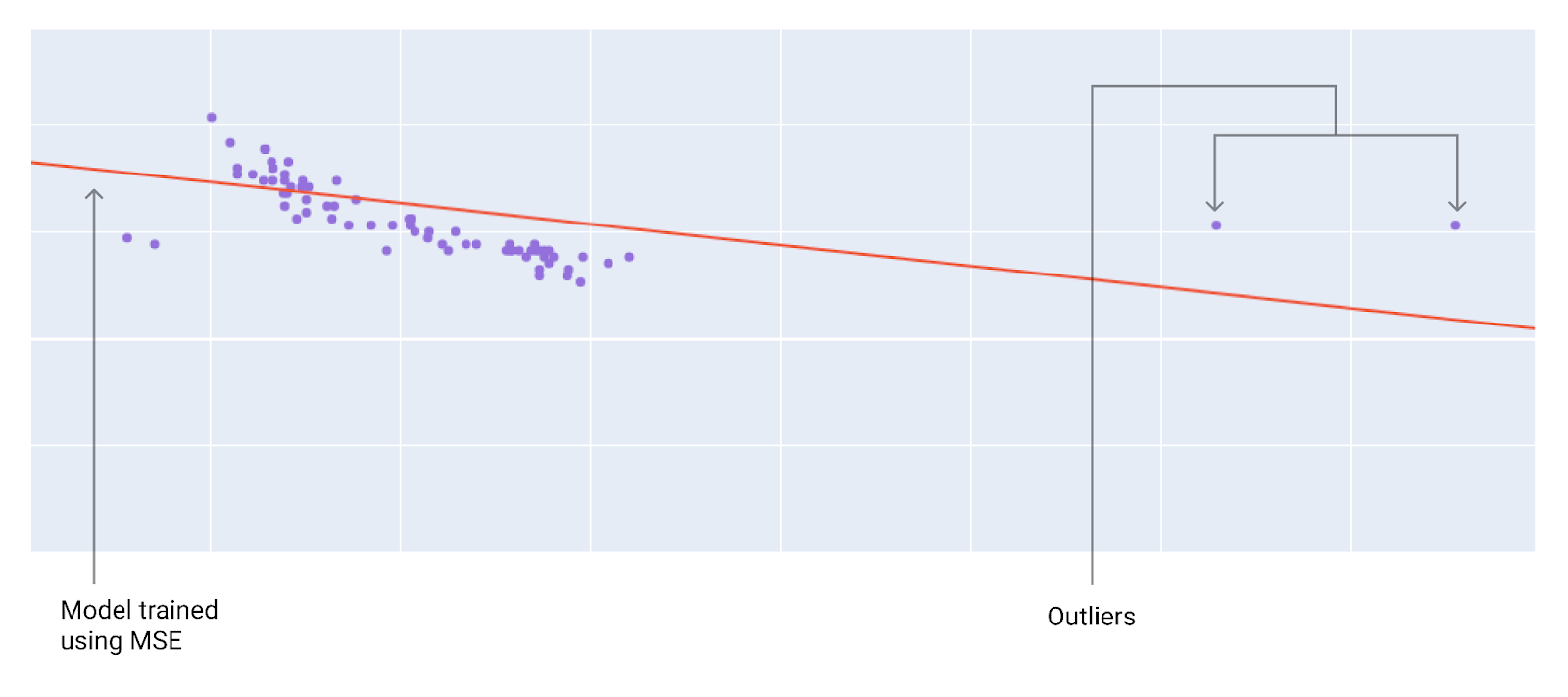
איור 9. הפסד MSE מקרב את המודל לערכים החריגים.
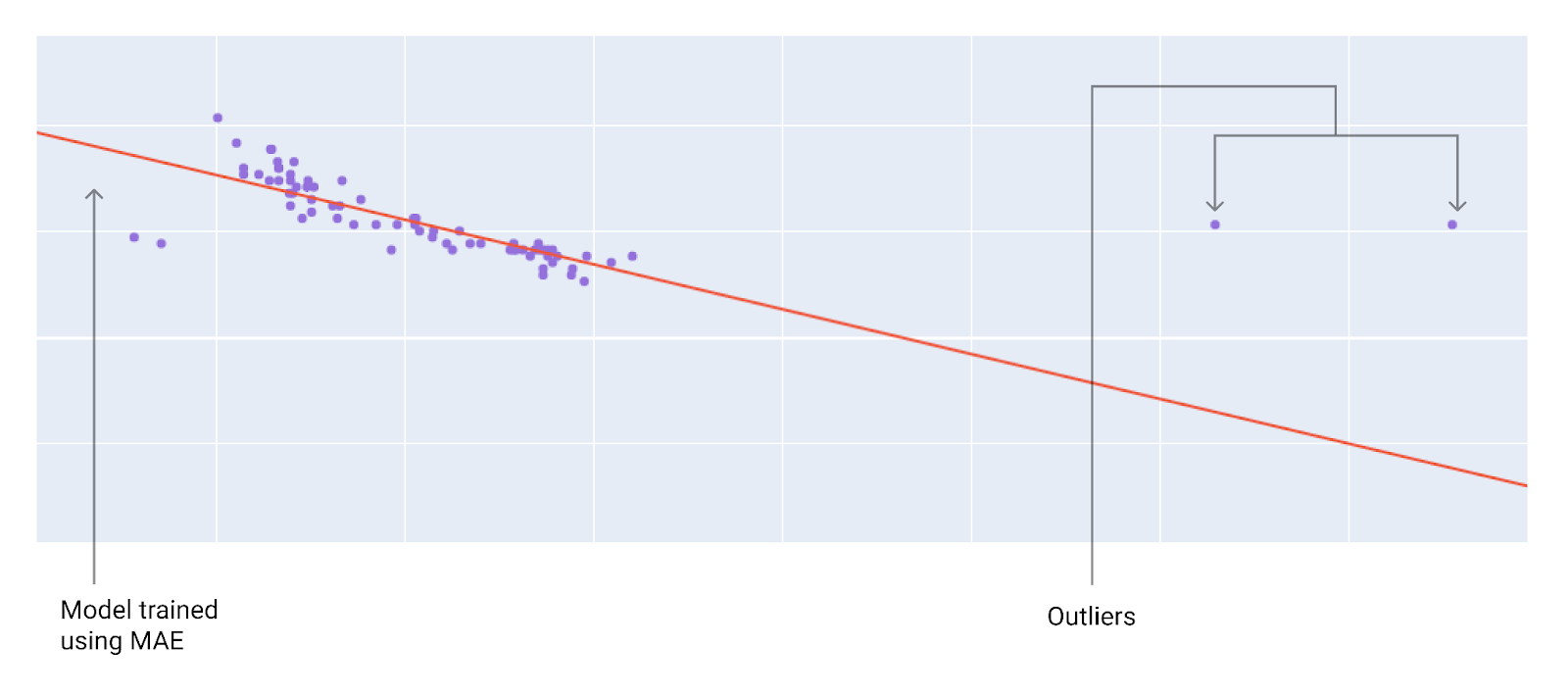
איור 10. הפסד MAE מרחיק את המודל מהערכים החריגים.
שימו לב לקשר בין המודל לבין הנתונים:
MSE. המודל קרוב יותר לערכים החריגים אבל רחוק יותר מרוב נקודות הנתונים האחרות.
MAE. המודל רחוק יותר מהערכים החריגים אבל קרוב יותר לרוב נקודות הנתונים האחרות.
בדיקת ההבנה
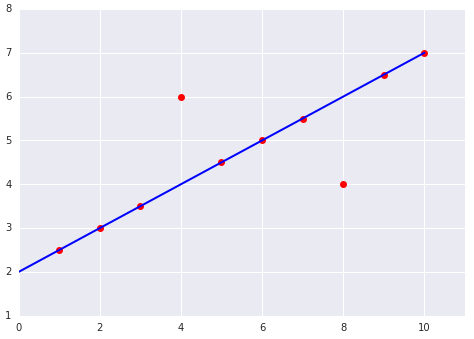
כדאי לעיין בשני הגרפים הבאים של התאמה של מודל ליניארי למערך נתונים:
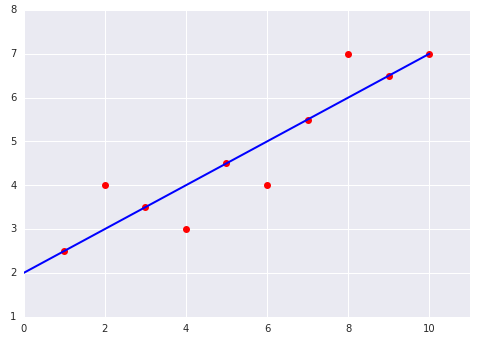
|
|
