زیان (Loss) یک معیار عددی است که میزان اشتباه پیشبینیهای یک مدل را توصیف میکند. زیان، فاصله بین پیشبینیهای مدل و برچسبهای واقعی را اندازهگیری میکند. هدف از آموزش یک مدل، به حداقل رساندن زیان و کاهش آن به کمترین مقدار ممکن است.
در تصویر زیر، میتوانید میزان زیان را به صورت فلشهایی که از نقاط داده به مدل کشیده شدهاند، تجسم کنید. فلشها نشان میدهند که پیشبینیهای مدل چقدر از مقادیر واقعی فاصله دارند.
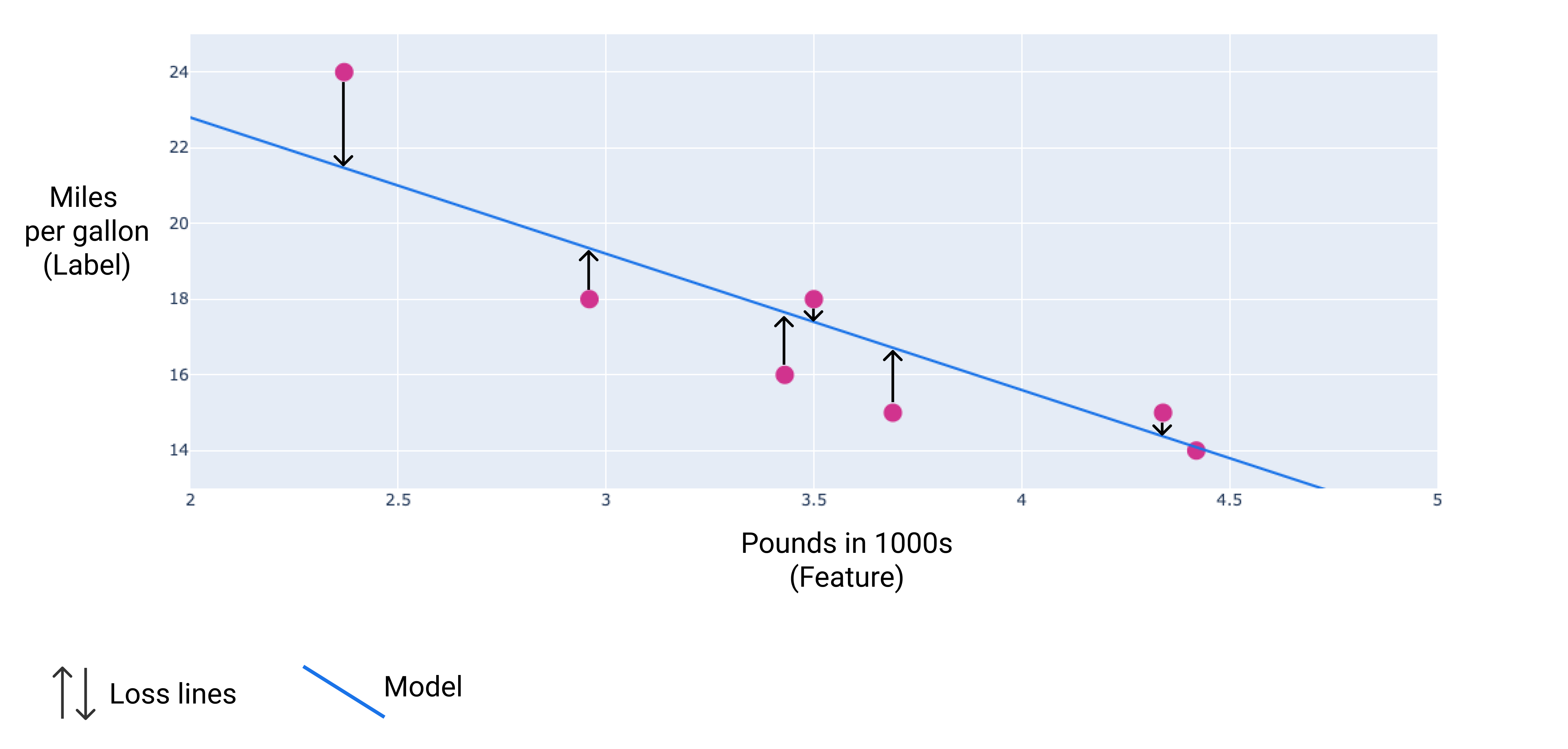
شکل ۸. میزان تلفات از مقدار واقعی تا مقدار پیشبینیشده اندازهگیری میشود.
فاصله از دست دادن
در آمار و یادگیری ماشین، زیان، تفاوت بین مقادیر پیشبینیشده و واقعی را اندازهگیری میکند. زیان بر فاصله بین مقادیر تمرکز دارد، نه جهت. برای مثال، اگر یک مدل ۲ را پیشبینی کند، اما مقدار واقعی ۵ باشد، برای ما مهم نیست که زیان منفی باشد (۲-۵$=-۳$). در عوض، برای ما مهم است که فاصله بین مقادیر ۳$ باشد. بنابراین، تمام روشهای محاسبه زیان، علامت را حذف میکنند.
دو روش رایج برای حذف علامت به شرح زیر است:
- قدر مطلق اختلاف بین مقدار واقعی و مقدار پیشبینی شده را در نظر بگیرید.
- اختلاف بین مقدار واقعی و مقدار پیشبینی شده را به توان دو برسانید.
انواع ضرر
در رگرسیون خطی، پنج نوع اصلی از دست دادن وجود دارد که در جدول زیر شرح داده شدهاند.
| نوع ضرر | تعریف | معادله |
|---|---|---|
| ضرر L 1 | مجموع قدر مطلق اختلاف بین مقادیر پیشبینیشده و مقادیر واقعی. | $ ∑ | مقدار واقعی - مقدار پیشبینیشده | $ |
| میانگین خطای مطلق (MAE) | میانگین L1 تلفات در مجموعهای از N مثال. | $ \frac{1}{N} ∑ | مقدار واقعی - مقدار پیشبینیشده | $ |
| ضرر L 2 | مجموع مربعات اختلاف بین مقادیر پیشبینیشده و مقادیر واقعی. | $ ∑(مقدار واقعی - مقدار پیشبینیشده)^2 $ |
| میانگین مربعات خطا (MSE) | میانگین L₂ تلفات در مجموعهای از N مثال. | $ \frac{1}{N} ∑ (مقدار واقعی - مقدار پیشبینیشده)^2 $ |
| جذر میانگین مربعات خطا (RMSE) | جذر میانگین مربعات خطا (MSE). | $ \sqrt{\frac{1}{N} ∑ (مقدار واقعی - مقدار پیشبینیشده)^2} $ |
تفاوت عملکردی بین خطای L1 و خطای L2 (یا بین MAE/RMSE و MSE) به توان دو رساندن است. وقتی تفاوت بین پیشبینی و برچسب زیاد باشد، به توان دو رساندن، خطای پیشبینی را بیشتر میکند. وقتی تفاوت کم باشد (کمتر از ۱)، به توان دو رساندن، خطای پیشبینی را کمتر میکند.
معیارهای زیان مانند MAE و RMSE ممکن است در برخی موارد استفاده نسبت به L2 loss یا MSE ارجحیت داشته باشند، زیرا تفسیر آنها توسط انسان آسانتر است، زیرا خطا را با استفاده از همان مقیاس مقدار پیشبینیشده مدل اندازهگیری میکنند.
هنگام پردازش چندین مثال به طور همزمان، توصیه میکنیم میانگین تلفات را در تمام مثالها، چه با استفاده از MAE، MSE یا RMSE، محاسبه کنید.
مثال محاسبه ضرر
با استفاده از بهترین خط برازش قبلی، ضرر L2 را برای یک مثال واحد محاسبه میکنیم. از بهترین خط برازش، مقادیر زیر را برای وزن و بایاس داشتیم:
- وزن: -۴.۶
- $ \small{بایاس: ۳۴} $
اگر مدل پیشبینی کند که یک ماشین ۲۳۷۰ پوندی ۲۳.۱ مایل در هر گالن مصرف میکند، اما در واقع ۲۶ مایل در هر گالن مصرف میکند، ما اتلاف L2 را به صورت زیر محاسبه میکنیم:
| ارزش | معادله | نتیجه |
|---|---|---|
| پیشبینی | $\small{بایاس + (وزن * ویژگی\ مقدار)}$ $\small{34 + (-4.6*2.37)}$ | $\کوچک{23.1}$ |
| ارزش واقعی | برچسب کوچک | \کوچک{26} |
| ضرر L 2 | $ \small{ (مقدار واقعی - مقدار پیشبینیشده)^2 } $ $\small{ (26 - 23.1)^2 }$ | $\کوچک{8.41}$ |
در این مثال، تلفات L2 برای آن نقطه داده واحد، ۸.۴۱ است.
انتخاب ضرر
تصمیمگیری در مورد استفاده از MAE یا MSE میتواند به مجموعه دادهها و نحوهی مدیریت پیشبینیهای خاص بستگی داشته باشد. اکثر مقادیر ویژگیها در یک مجموعه دادهها معمولاً در یک محدودهی مشخص قرار میگیرند. به عنوان مثال، خودروها معمولاً بین ۲۰۰۰ تا ۵۰۰۰ پوند وزن دارند و بین ۸ تا ۵۰ مایل در هر گالن مصرف میکنند. یک ماشین ۸۰۰۰ پوندی یا ماشینی که ۱۰۰ مایل در هر گالن مصرف میکند، خارج از محدودهی معمول است و به عنوان یک دادهی پرت در نظر گرفته میشود.
یک داده پرت همچنین میتواند به میزان فاصله پیشبینیهای مدل از مقادیر واقعی اشاره داشته باشد. به عنوان مثال، ۳۰۰۰ پوند در محدوده وزن معمول خودرو و ۴۰ مایل در هر گالن در محدوده بهرهوری سوخت معمول است. با این حال، یک ماشین ۳۰۰۰ پوندی که ۴۰ مایل در هر گالن مصرف میکند، از نظر پیشبینی مدل، یک داده پرت خواهد بود زیرا مدل پیشبینی میکند که یک ماشین ۳۰۰۰ پوندی حدود ۲۰ مایل در هر گالن مصرف خواهد کرد.
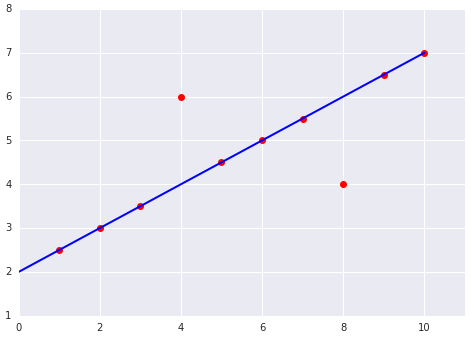
هنگام انتخاب بهترین تابع زیان، در نظر بگیرید که میخواهید مدل چگونه با دادههای پرت رفتار کند. برای مثال، MSE مدل را بیشتر به سمت دادههای پرت حرکت میدهد، در حالی که MAE این کار را نمیکند. زیان L2 جریمه بسیار بیشتری برای یک داده پرت نسبت به زیان L1 متحمل میشود. برای مثال، تصاویر زیر مدلی را نشان میدهند که با استفاده از MAE آموزش دیده و مدلی را که با استفاده از MSE آموزش دیده است. خط قرمز نشان دهنده یک مدل کاملاً آموزش دیده است که برای پیشبینی استفاده خواهد شد. دادههای پرت به مدل آموزش دیده با MSE نزدیکتر هستند تا به مدل آموزش دیده با MAE.
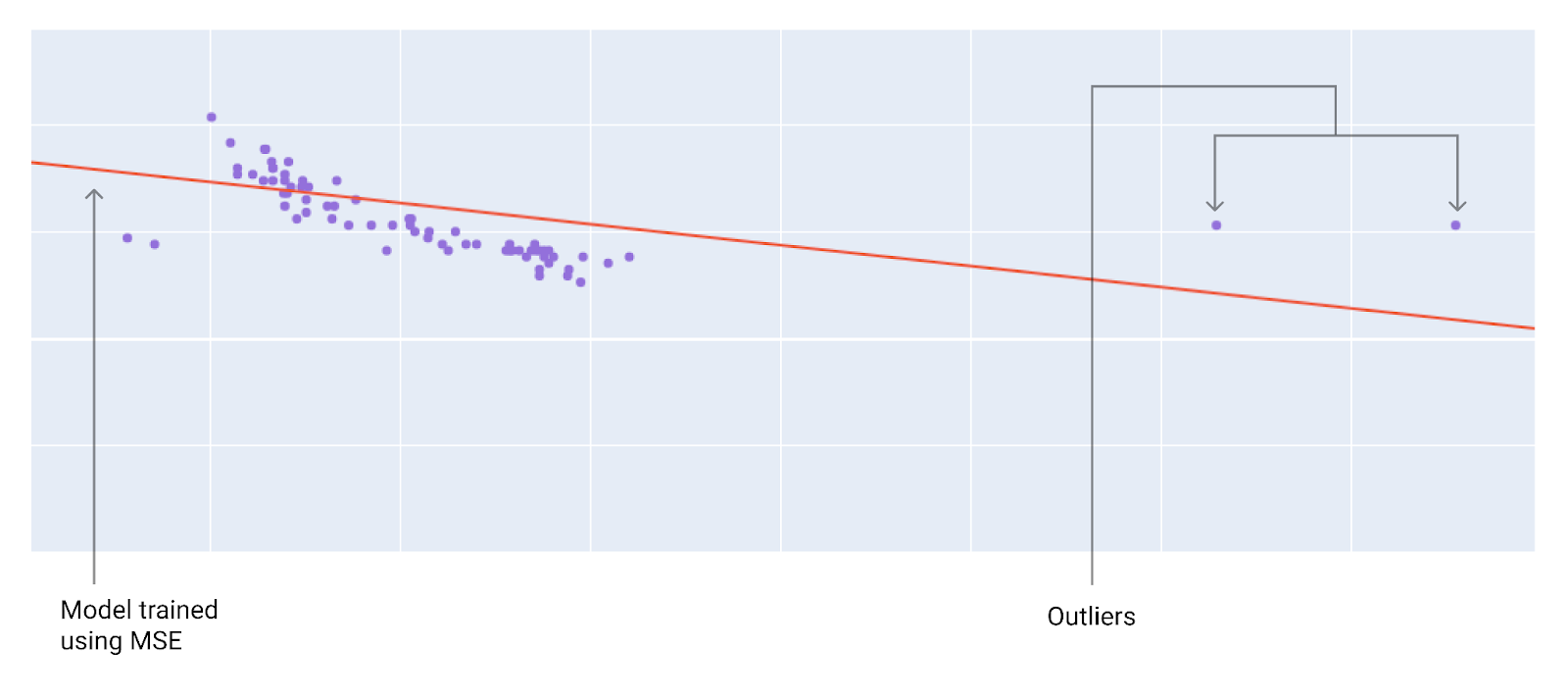
شکل 9. زیان MSE مدل را به دادههای پرت نزدیکتر میکند.
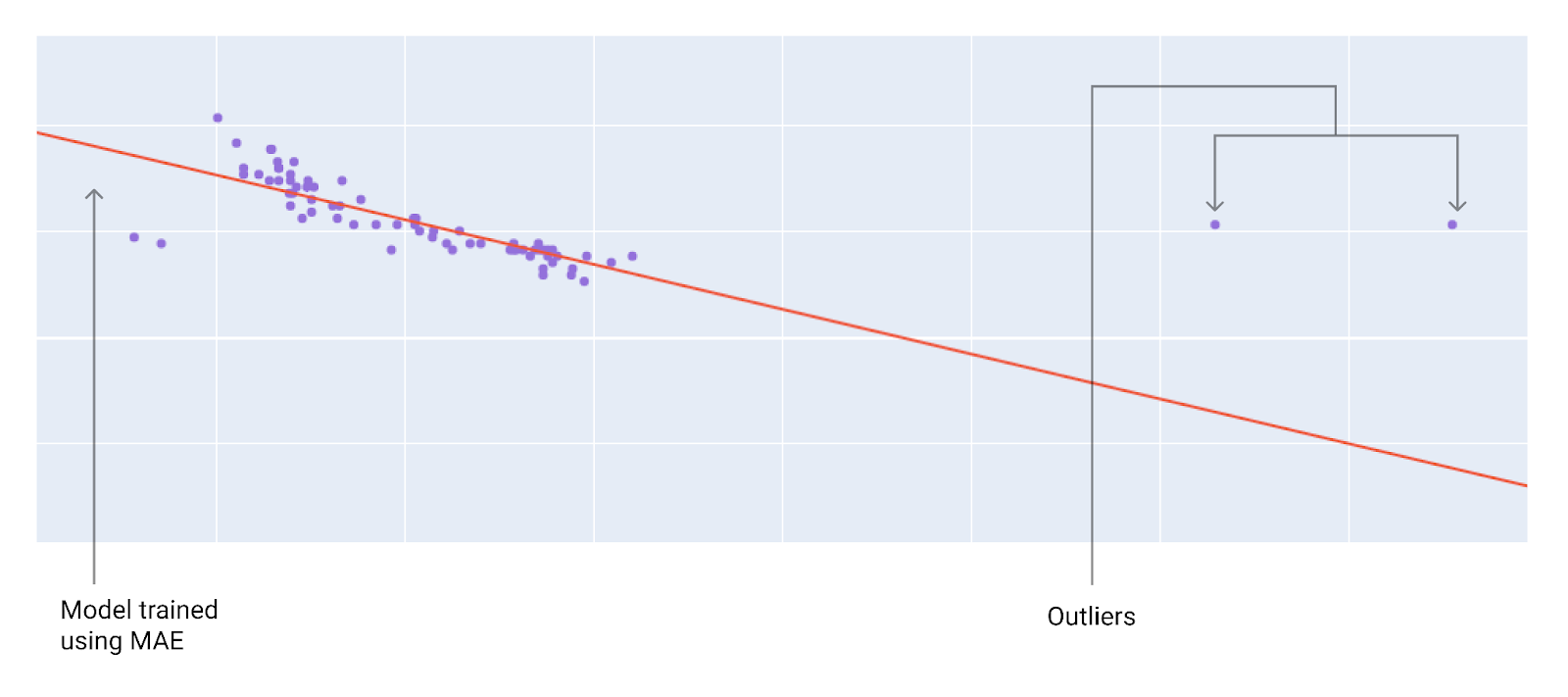
شکل 10. زیان MAE مدل را از دادههای پرت دورتر نگه میدارد.
به رابطه بین مدل و دادهها توجه کنید:
MSE . مدل به دادههای پرت نزدیکتر است اما از اکثر نقاط داده دیگر دورتر است.
MAE . مدل از دادههای پرت دورتر است اما به اکثر نقاط داده دیگر نزدیکتر است.
درک خود را بررسی کنید
دو نمودار زیر از یک مدل خطی برازش یافته به یک مجموعه داده را در نظر بگیرید:
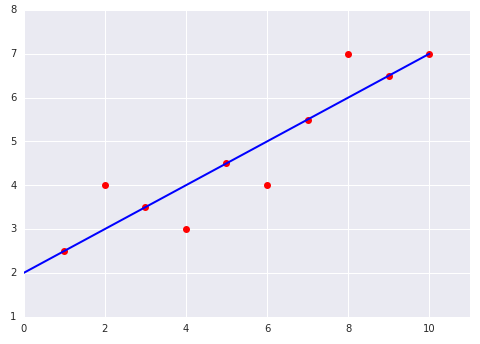 |  |
