ক্ষতি হল একটি সংখ্যাসূচক পরিমাপ যা বর্ণনা করে যে একটি মডেলের ভবিষ্যদ্বাণী কতটা ভুল। ক্ষতি মডেলের ভবিষ্যদ্বাণী এবং প্রকৃত লেবেলের মধ্যে দূরত্ব পরিমাপ করে। একটি মডেলকে প্রশিক্ষণ দেওয়ার লক্ষ্য হল ক্ষতি কমিয়ে আনা, এটিকে সর্বনিম্ন সম্ভাব্য মান পর্যন্ত কমিয়ে আনা।
নিচের ছবিতে, আপনি ডেটা পয়েন্ট থেকে মডেলের দিকে টানা তীর হিসাবে ক্ষতি কল্পনা করতে পারেন। তীরগুলি দেখায় যে মডেলের ভবিষ্যদ্বাণীগুলি প্রকৃত মান থেকে কতটা দূরে।
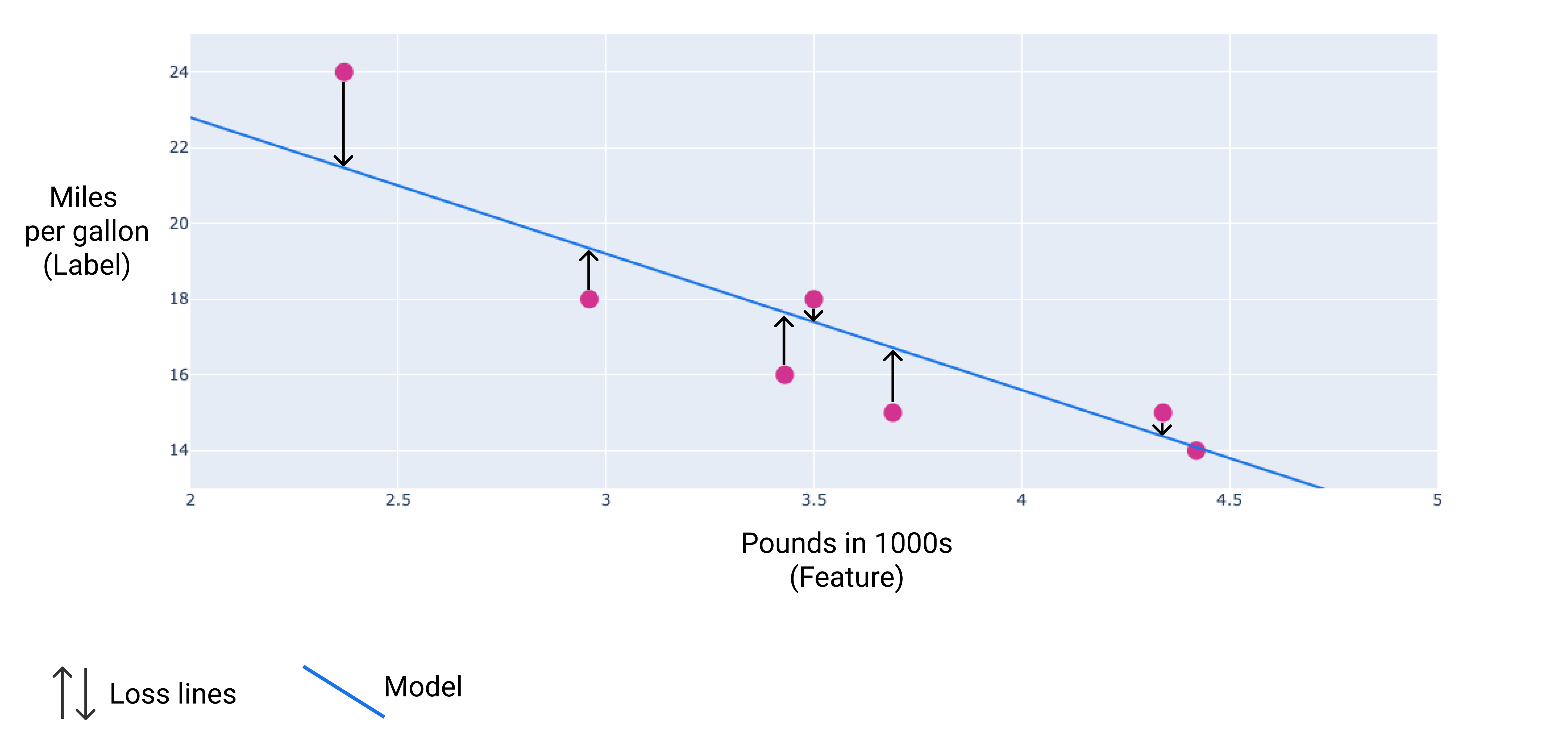
চিত্র ৮। ক্ষতির পরিমাণ প্রকৃত মান থেকে পূর্বাভাসিত মান পর্যন্ত পরিমাপ করা হয়।
ক্ষতির দূরত্ব
পরিসংখ্যান এবং মেশিন লার্নিং-এ, ক্ষতি পূর্বাভাসিত এবং প্রকৃত মানের মধ্যে পার্থক্য পরিমাপ করে। ক্ষতি দিকনির্দেশনার উপর নয়, মানের মধ্যে দূরত্বের উপর দৃষ্টি নিবদ্ধ করে। উদাহরণস্বরূপ, যদি একটি মডেল 2 ভবিষ্যদ্বাণী করে, কিন্তু প্রকৃত মান 5 হয়, তাহলে আমরা ক্ষতি নেতিবাচক কিনা তা পরোয়া করি না ($ 2-5=-3 $)। পরিবর্তে, আমরা গুরুত্ব দিই যে মানগুলির মধ্যে দূরত্ব $ 3 $। সুতরাং, ক্ষতি গণনা করার সমস্ত পদ্ধতি চিহ্নটি সরিয়ে দেয়।
চিহ্নটি অপসারণের দুটি সবচেয়ে সাধারণ পদ্ধতি হল:
- প্রকৃত মান এবং পূর্বাভাসের মধ্যে পার্থক্যের পরম মান নিন।
- প্রকৃত মান এবং পূর্বাভাসের মধ্যে পার্থক্যের বর্গ করুন।
ক্ষতির প্রকারভেদ
রৈখিক রিগ্রেশনে, পাঁচটি প্রধান ধরণের ক্ষতি রয়েছে, যা নিম্নলিখিত সারণীতে বর্ণিত হয়েছে।
| ক্ষতির ধরণ | সংজ্ঞা | সমীকরণ |
|---|---|---|
| এল ১ ক্ষতি | পূর্বাভাসিত মান এবং প্রকৃত মানের মধ্যে পার্থক্যের পরম মানের যোগফল। | $ ∑ | প্রকৃত\ মান - পূর্বাভাসিত\ মান | $ |
| গড় পরম ত্রুটি (MAE) | N উদাহরণের একটি সেট জুড়ে L 1 ক্ষতির গড়। | $ \frac{1}{N} ∑ | প্রকৃত\ মান - পূর্বাভাসিত\ মান | $ |
| L 2 ক্ষতি | পূর্বাভাসিত মান এবং প্রকৃত মানের মধ্যে বর্গ পার্থক্যের যোগফল। | $ ∑(প্রকৃত\ মান - পূর্বাভাসিত\ মান)^2 $ |
| গড় বর্গ ত্রুটি (MSE) | N উদাহরণের একটি সেট জুড়ে L 2 ক্ষতির গড়। | $ \frac{1}{N} ∑ (প্রকৃত\ মান - পূর্বাভাসিত\ মান)^2 $ |
| মূল গড় বর্গ ত্রুটি (RMSE) | গড় বর্গ ত্রুটির (MSE) বর্গমূল। | $ \sqrt{\frac{1}{N} ∑ (প্রকৃত\ মান - পূর্বাভাসিত\ মান)^2} $ |
L 1 ক্ষতি এবং L 2 ক্ষতির (অথবা MAE/RMSE এবং MSE এর মধ্যে) কার্যকরী পার্থক্য হল বর্গকরণ। যখন পূর্বাভাস এবং লেবেলের মধ্যে পার্থক্য বড় হয়, তখন বর্গকরণ ক্ষতিকে আরও বড় করে তোলে। যখন পার্থক্য ছোট হয় (1 এর কম), তখন বর্গকরণ ক্ষতিকে আরও ছোট করে তোলে।
কিছু ব্যবহারের ক্ষেত্রে L 2 ক্ষতি বা MSE এর চেয়ে MAE এবং RMSE এর মতো ক্ষতির মেট্রিক্স বেশি পছন্দনীয় হতে পারে কারণ এগুলি মানুষের দ্বারা ব্যাখ্যাযোগ্য হওয়ার প্রবণতা বেশি, কারণ তারা মডেলের পূর্বাভাসিত মানের মতো একই স্কেল ব্যবহার করে ত্রুটি পরিমাপ করে।
একসাথে একাধিক উদাহরণ প্রক্রিয়া করার সময়, আমরা MAE, MSE, অথবা RMSE ব্যবহার করেই হোক না কেন, সমস্ত উদাহরণের ক্ষতির গড় নির্ধারণ করার পরামর্শ দিই।
ক্ষতি গণনার উদাহরণ
পূর্ববর্তী সেরা ফিট লাইন ব্যবহার করে, আমরা একটি একক উদাহরণের জন্য L 2 ক্ষতি গণনা করব। সেরা ফিট লাইন থেকে, আমাদের ওজন এবং পক্ষপাতের জন্য নিম্নলিখিত মানগুলি ছিল:
- $ \ছোট{ওজন: -৪.৬} $
- $ \ছোট{পক্ষপাত: ৩৪} $
যদি মডেলটি ভবিষ্যদ্বাণী করে যে ২,৩৭০ পাউন্ড ওজনের একটি গাড়ি প্রতি গ্যালনে ২৩.১ মাইল পায়, কিন্তু আসলে এটি প্রতি গ্যালনে ২৬ মাইল পায়, তাহলে আমরা নিম্নরূপ L 2 ক্ষতি গণনা করব:
| মূল্য | সমীকরণ | ফলাফল |
|---|---|---|
| ভবিষ্যদ্বাণী | $\ছোট{পক্ষপাত + (ওজন * বৈশিষ্ট্য\ মান)}$ $\ছোট{৩৪ + (-৪.৬*২.৩৭)}$ | $\ছোট{২৩.১}$ |
| প্রকৃত মান | $ \ছোট{ লেবেল } $ | $ \ছোট{ 26 } $ |
| L 2 ক্ষতি | $ \ছোট{ (প্রকৃত\ মান - পূর্বাভাসিত\ মান)^2 } $ $\ছোট{ (২৬ - ২৩.১)^২ }$ | $\ছোট{৮.৪১}$ |
এই উদাহরণে, সেই একক ডেটা পয়েন্টের জন্য L 2 ক্ষতি হল 8.41।
ক্ষতি বেছে নেওয়া
MAE নাকি MSE ব্যবহার করবেন তা নির্ধারণ ডেটাসেট এবং আপনি কীভাবে নির্দিষ্ট ভবিষ্যদ্বাণী পরিচালনা করতে চান তার উপর নির্ভর করতে পারে। একটি ডেটাসেটের বেশিরভাগ বৈশিষ্ট্যের মান সাধারণত একটি নির্দিষ্ট পরিসরের মধ্যে পড়ে। উদাহরণস্বরূপ, গাড়িগুলি সাধারণত 2000 থেকে 5000 পাউন্ডের মধ্যে হয় এবং প্রতি গ্যালনে 8 থেকে 50 মাইলের মধ্যে যায়। একটি 8,000-পাউন্ডের গাড়ি, অথবা একটি গাড়ি যা প্রতি গ্যালনে 100 মাইল পায়, সাধারণ পরিসরের বাইরে এবং এটিকে একটি বহিরাগত হিসাবে বিবেচনা করা হবে।
একটি আউটলায়ার বলতে বোঝায় যে, একটি মডেলের ভবিষ্যদ্বাণী বাস্তব মান থেকে কতটা দূরে। উদাহরণস্বরূপ, ৩,০০০ পাউন্ড হল সাধারণ গাড়ির ওজনের সীমার মধ্যে, এবং প্রতি গ্যালনে ৪০ মাইল হল সাধারণ জ্বালানি-দক্ষতার সীমার মধ্যে। যাইহোক, ৩,০০০ পাউন্ড ওজনের একটি গাড়ি যা প্রতি গ্যালনে ৪০ মাইল ওজন করে, তা মডেলের ভবিষ্যদ্বাণীর পরিপ্রেক্ষিতে একটি আউটলায়ার হবে কারণ মডেলটি ভবিষ্যদ্বাণী করবে যে ৩,০০০ পাউন্ড ওজনের একটি গাড়ি প্রতি গ্যালনে প্রায় ২০ মাইল ওজন করবে।
সেরা ক্ষতির ফাংশন নির্বাচন করার সময়, বিবেচনা করুন যে মডেলটি বহির্মুখীদের সাথে কীভাবে আচরণ করবে। উদাহরণস্বরূপ, MSE মডেলটিকে বহির্মুখীদের দিকে বেশি নিয়ে যায়, যেখানে MAE তা করে না। L 2 ক্ষতি L 1 ক্ষতির চেয়ে বহির্মুখীদের জন্য অনেক বেশি জরিমানা বহন করে। উদাহরণস্বরূপ, নিম্নলিখিত চিত্রগুলিতে MAE ব্যবহার করে প্রশিক্ষিত একটি মডেল এবং MSE ব্যবহার করে প্রশিক্ষিত একটি মডেল দেখানো হয়েছে। লাল রেখাটি একটি সম্পূর্ণ প্রশিক্ষিত মডেলকে প্রতিনিধিত্ব করে যা ভবিষ্যদ্বাণী করতে ব্যবহৃত হবে। বহির্মুখীরা MAE ব্যবহার করে প্রশিক্ষিত মডেলের তুলনায় MSE ব্যবহার করে প্রশিক্ষিত মডেলের কাছাকাছি।
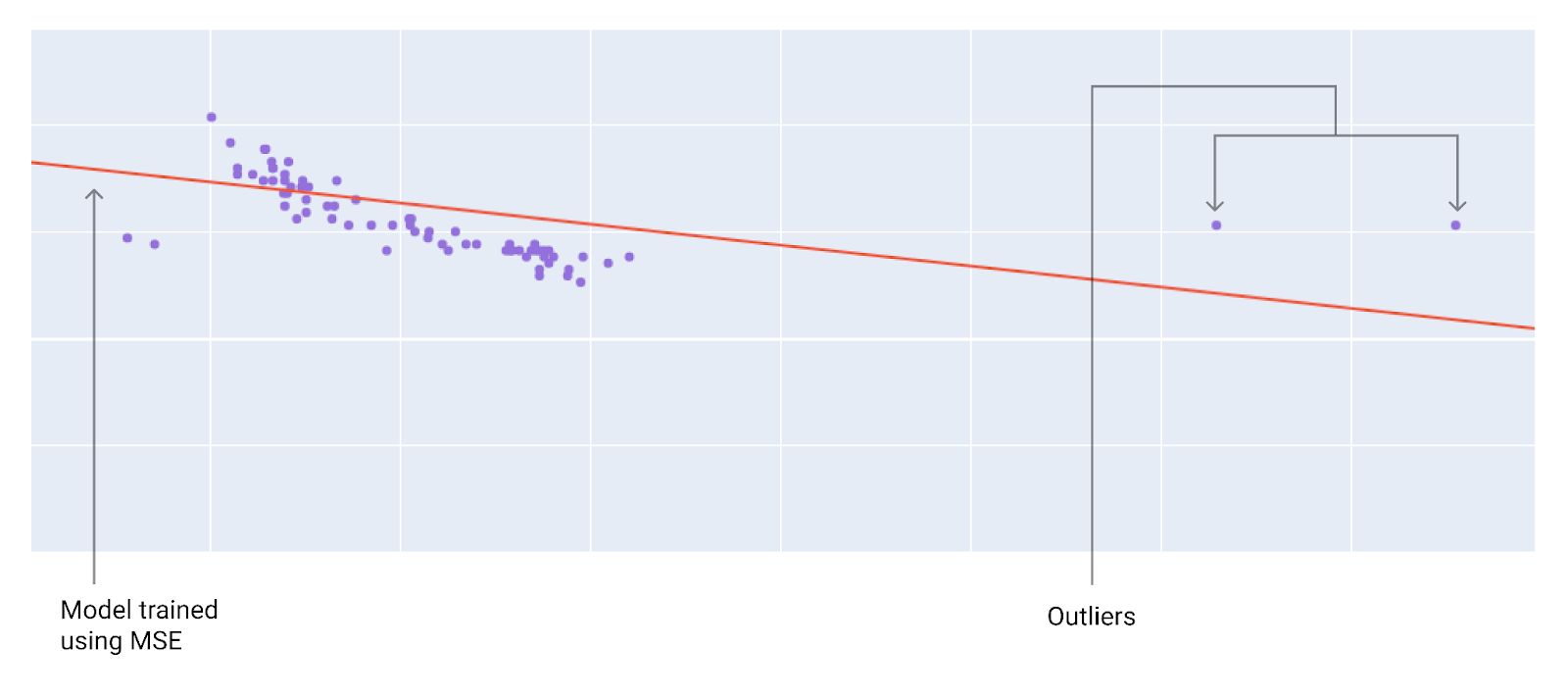
চিত্র ৯। MSE ক্ষতি মডেলটিকে বহির্মুখীদের কাছাকাছি নিয়ে যায়।
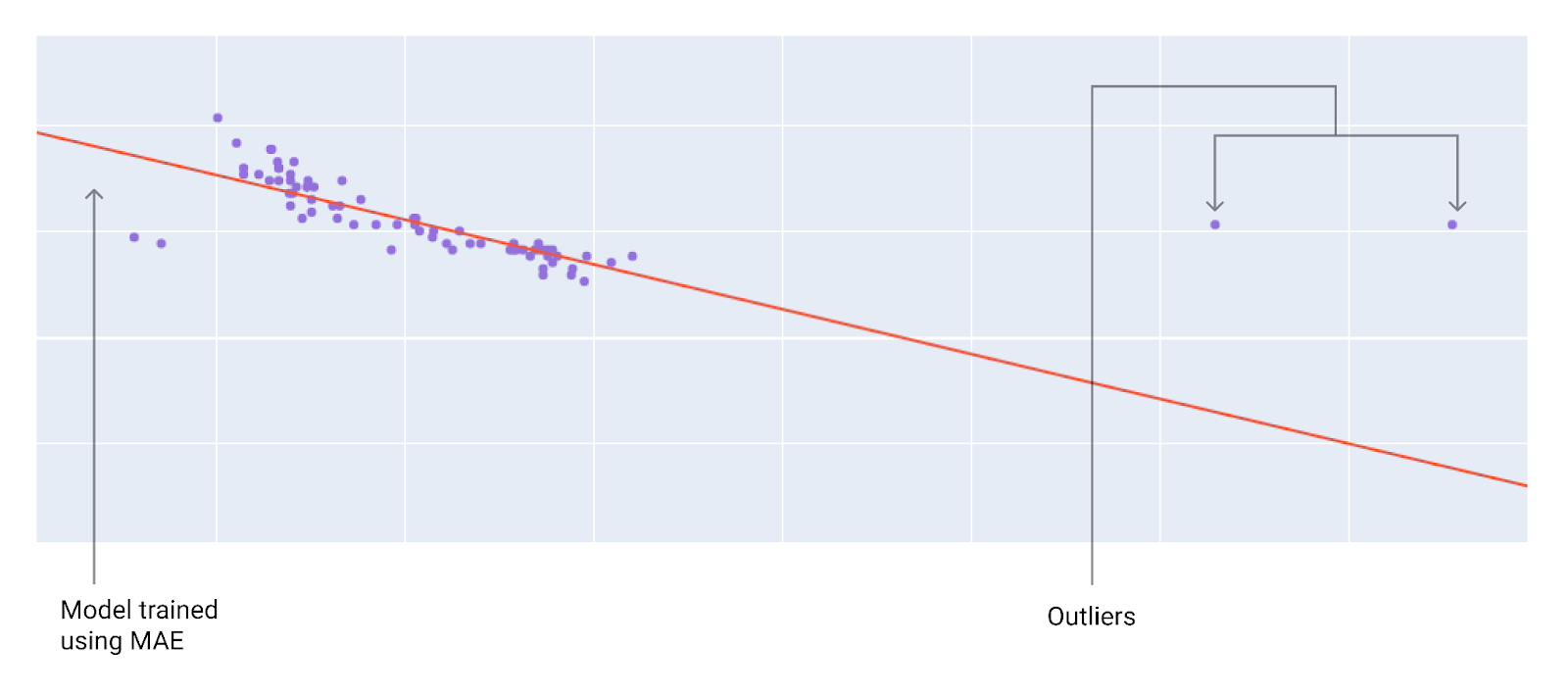
চিত্র ১০। MAE ক্ষতি মডেলটিকে বহিরাগতদের থেকে অনেক দূরে রাখে।
মডেল এবং ডেটার মধ্যে সম্পর্ক লক্ষ্য করুন:
MSE । মডেলটি বহির্মুখীদের কাছাকাছি কিন্তু অন্যান্য বেশিরভাগ ডেটা পয়েন্ট থেকে আরও দূরে।
MAE । মডেলটি বহির্মুখী থেকে আরও দূরে কিন্তু অন্যান্য বেশিরভাগ ডেটা পয়েন্টের কাছাকাছি।
তোমার বোধগম্যতা পরীক্ষা করো
একটি ডেটাসেটের সাথে মানানসই একটি রৈখিক মডেলের নিম্নলিখিত দুটি প্লট বিবেচনা করুন:
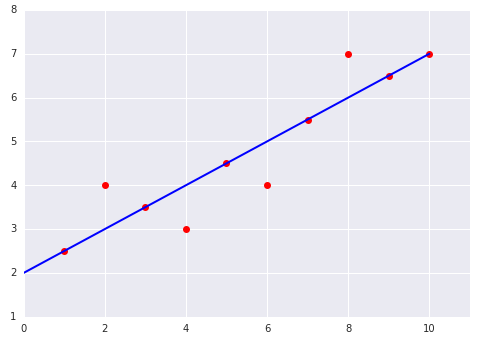 | 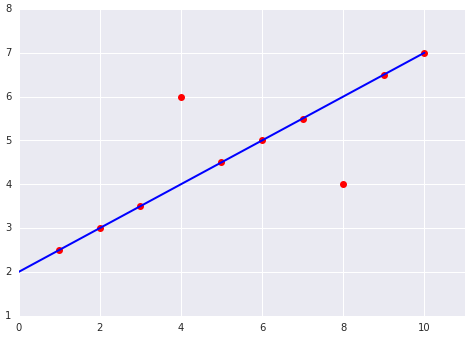 |
