損失は、モデルの予測の精度がどの程度低いかを表す数値指標です。損失は、モデルの予測と実際のラベルの間の距離を測定します。モデルのトレーニングの目標は、損失を最小限に抑え、可能な限り低い値にすることです。
次の図では、損失はデータポイントからモデルに描画された矢印として視覚化されています。矢印は、モデルの予測が実際の値からどのくらい離れているかを示しています。
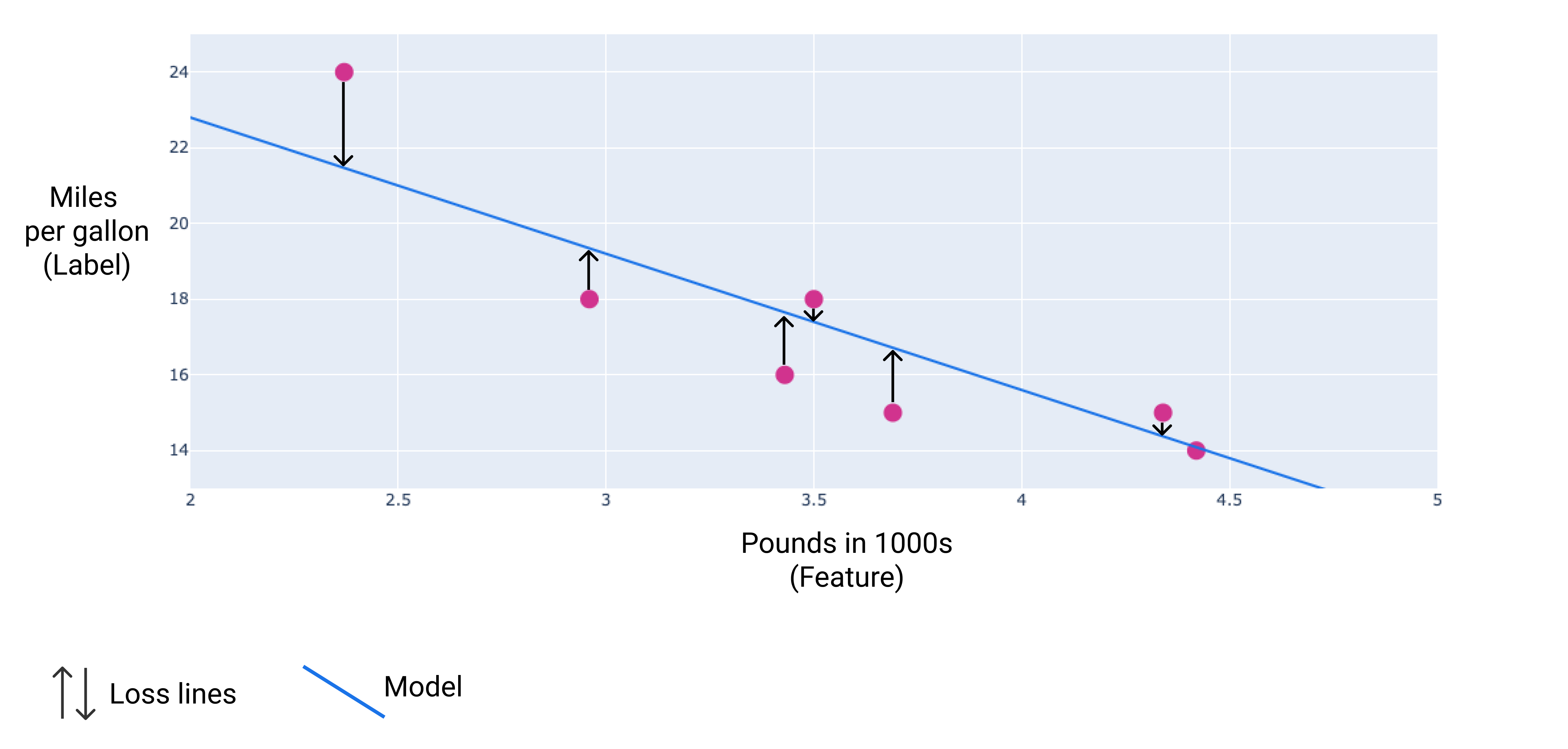
図 8. 損失は、実際の値から予測値までの距離で測定されます。
損失距離
統計と ML では、損失は予測値と正解値の差を測定します。損失は、方向ではなく値間の距離に焦点を当てます。たとえば、モデルが 2 と予測したのに、実際の値が 5 の場合、損失が負の値($ 2-5=-3 $)であることは問題ではありません。値間の距離が $ 3 $ であることが重要です。したがって、損失を計算するすべての方法で符号が削除されます。
符号を削除する最も一般的な方法は次の 2 つです。
- 実際の値と予測値の差の絶対値を取得します。
- 実際の値と予測値の差を 2 乗します。
損失の種類
線形回帰には、次の表に示す 4 つの主な損失タイプがあります。
| 損失タイプ | 定義 | 計算式 |
|---|---|---|
| L1 損失 | 予測値と実際の値の差の絶対値の合計。 | $ ∑ | 実際の値 - 予測値 | $ |
| 平均絶対誤差(MAE) | *N* 個のサンプルのセットにおける L1 損失の平均。 | $ \frac{1}{N} ∑ | 実測値 - 予測値 | $ |
| L2 損失 | 予測値と実際の値の差の二乗和。 | $ ∑(実際の値 - 予測値)^2 $ |
| 平均二乗誤差(MSE) | *N* 個のサンプルセット全体の L2 損失の平均。 | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
L1 損失と L2 損失(または MAE と MSE)の機能的な違いは、二乗です。予測とラベルの差が大きい場合、二乗することで損失がさらに大きくなります。差が小さい(1 未満)場合、2 乗すると損失はさらに小さくなります。
複数の例を一度に処理する場合は、MAE と MSE のどちらを使用する場合でも、すべての例の損失を平均することをおすすめします。
損失の計算例
前の最適な直線を使用して、単一の例の L2 損失を計算します。最適な適合線から、重みとバイアスの値は次のようになります。
- $ \small{重み: -4.6} $
- $ \small{バイアス: 34} $
モデルが 2,370 ポンドの自動車の燃費を 23.1 マイル / ガロンと予測したが、実際には 26 マイル / ガロンである場合、L2 損失は次のように計算されます。
| 値 | 計算式 | 結果 |
|---|---|---|
| 予測 | $\small{バイアス + (重み * 特徴値)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| 実際の値 | $ \small{ label } $ | $ \small{ 26 } $ |
| L2 損失 | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
この例では、その単一のデータポイントの L2 損失は 8.41 です。
損失を選択する
MAE を使用するか MSE を使用するかは、データセットと特定の予測の処理方法によって異なります。通常、データセット内のほとんどの特徴値は、明確な範囲内に収まります。たとえば、自動車の重量は通常 2,000 ~ 5,000 ポンドで、1 ガロンあたりの走行距離は 8 ~ 50 マイルです。8,000 ポンドの車や、燃費が 100 マイル / ガロンの車は、一般的な範囲外であり、外れ値と見なされます。
外れ値は、モデルの予測が実際の値からどのくらい離れているかを表すこともあります。たとえば、3,000 ポンドは一般的な車の重量範囲内であり、40 マイル / ガロンは一般的な燃費範囲内です。ただし、3,000 ポンドの自動車で燃費が 40 マイル / ガロンの場合、モデルの予測では外れ値になります。モデルでは、3,000 ポンドの自動車の燃費は 20 マイル / ガロン程度と予測されるためです。
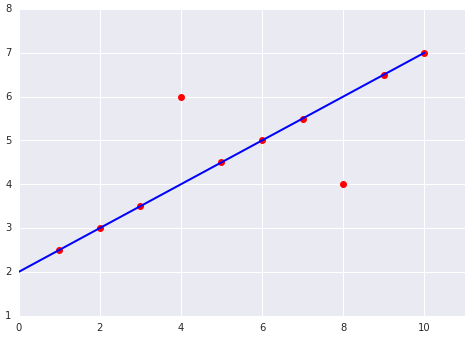
最適な損失関数を選択する際は、モデルで外れ値をどのように処理するかを検討してください。たとえば、MSE はモデルを外れ値に近づけますが、MAE は近づけません。L2 損失は、L1 損失よりも外れ値に対してはるかに大きなペナルティを課します。たとえば、次の画像は、MAE を使用してトレーニングされたモデルと、MSE を使用してトレーニングされたモデルを示しています。赤い線は、予測に使用される完全にトレーニングされたモデルを表します。外れ値は、MAE でトレーニングされたモデルよりも MSE でトレーニングされたモデルに近い。
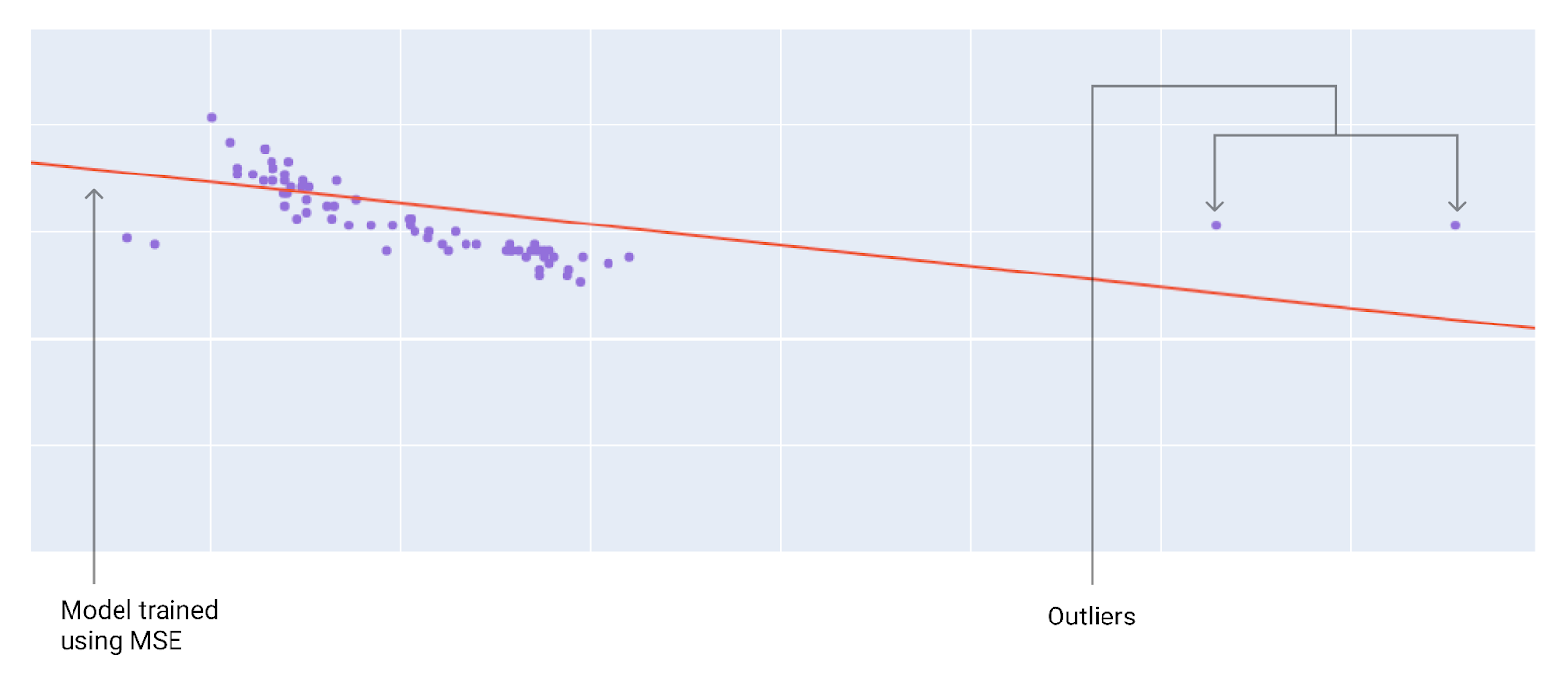
図 9. MSE でトレーニングされたモデルは、外れ値に近づきます。
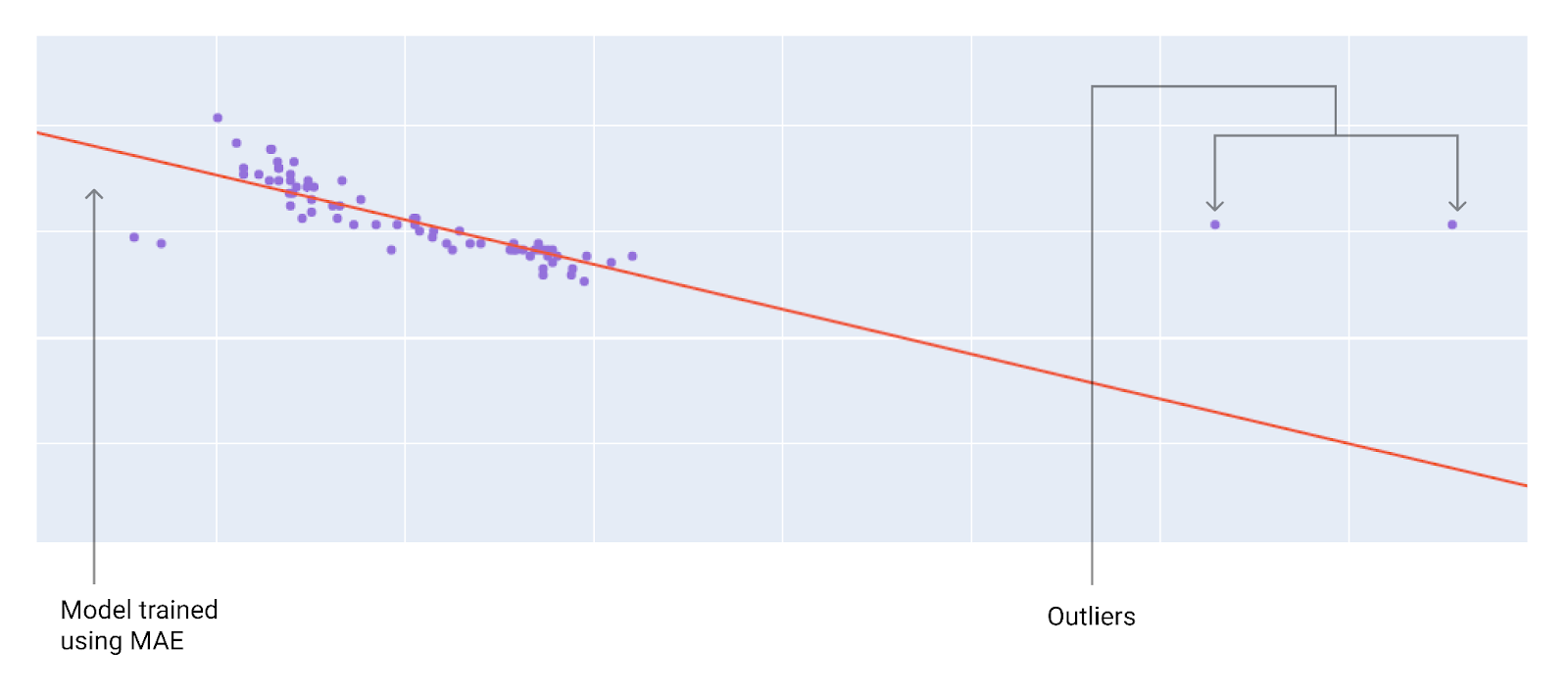
図 10. MAE でトレーニングされたモデルは、外れ値から遠くなります。
モデルとデータの関係に注意してください。
MSE。モデルは外れ値に近いですが、他のほとんどのデータポイントからは離れています。
MAE。モデルは外れ値から遠く離れていますが、他のほとんどのデータポイントには近くなっています。
理解度チェック
データセットに適合した線形モデルの次の 2 つのプロットについて考えてみましょう。
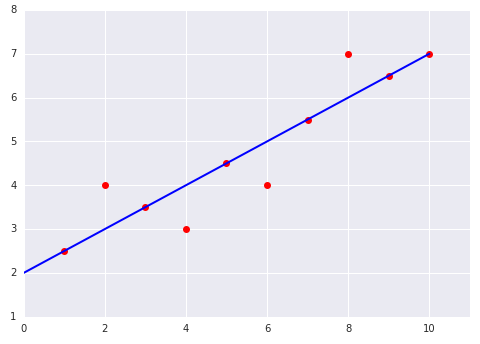
|
|
