الخسارة هي مقياس رقمي يصف مدى خطأ توقّعات النموذج. تقيس الخسارة المسافة بين التوقعات التي يقدّمها النموذج والتصنيفات الفعلية. والهدف من تدريب النموذج هو تقليل الخسارة إلى أدنى قيمة ممكنة.
في الصورة التالية، يمكنك تصوّر الخسارة على شكل أسهم مرسومة من نقاط البيانات إلى النموذج. توضّح الأسهم مدى بُعد التوقّعات التي يقدّمها النموذج عن القيم الفعلية.
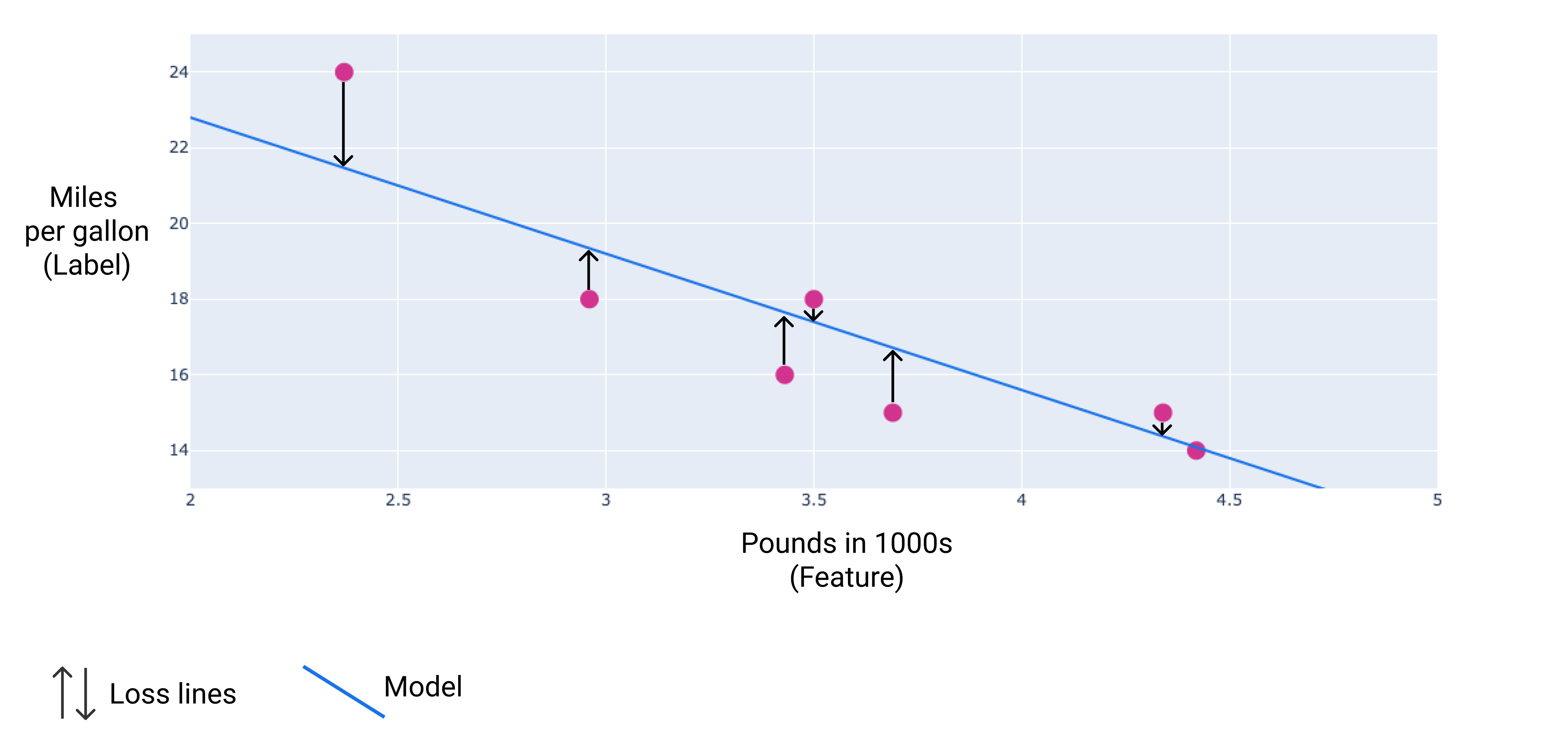
الشكل 8 يتم قياس الخسارة من القيمة الفعلية إلى القيمة المتوقّعة.
مسافة الفقدان
في الإحصاء وتعلُّم الآلة، يقيس مقياس الخسارة الفرق بين القيم المتوقّعة والفعلية. يركّز مقياس الخسارة على المسافة بين القيم، وليس على الاتجاه. على سبيل المثال، إذا توقّع أحد النماذج القيمة 2، ولكن القيمة الفعلية كانت 5، لا يهمّنا أن تكون الخسارة سالبة (2-5=-3)، بل يهمّنا أن تكون المسافة بين القيمتين هي 3. وبالتالي، تزيل جميع طرق حساب الخسارة الإشارة.
في ما يلي الطريقتان الأكثر شيوعًا لإزالة العلامة:
- يتم احتساب القيمة المطلقة للفرق بين القيمة الفعلية والقيمة المتوقّعة.
- ربِّع الفرق بين القيمة الفعلية والقيمة المتوقّعة.
أنواع الخسائر
في الانحدار الخطي، هناك أربعة أنواع رئيسية من الخسارة، وهي موضّحة في الجدول التالي.
| نوع الخسارة | التعريف | معادلة |
|---|---|---|
| فقدان L1 | يشير ذلك المصطلح إلى مجموع القيم المطلقة للفرق بين القيم المتوقَّعة والقيم الفعلية. | $ ∑ | actual\ value - predicted\ value | $ |
| متوسّط الخطأ المطلق (MAE) | متوسط خسائر L1 على مجموعة من *N* الأمثلة | $ \frac{1}{N} ∑ | actual\ value - predicted\ value | $ |
| فقدان L2 | يشير ذلك المصطلح إلى مجموع الفَرق التربيعي بين القيم المتوقَّعة والقيم الفعلية. | $ ∑(actual\ value - predicted\ value)^2 $ |
| الخطأ التربيعي المتوسّط (MSE) | متوسط خسائر L2 على مجموعة من *N* الأمثلة | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
الفرق الوظيفي بين خسارة L1 وخسارة L2(أو بين متوسط الخطأ المطلق ومتوسط الخطأ التربيعي) هو التربيع. عندما يكون الفرق بين التوقّع والتصنيف كبيرًا، يؤدي التربيع إلى زيادة الخسارة. عندما يكون الفرق صغيرًا (أقل من 1)، يؤدي التربيع إلى تقليل الخسارة.
عند معالجة أمثلة متعددة في الوقت نفسه، ننصحك بحساب متوسط الخسائر على مستوى جميع الأمثلة، سواء كنت تستخدم متوسط الخطأ المطلق أو متوسط الخطأ التربيعي.
مثال على احتساب الخسارة
باستخدام خط أفضل تطابق السابق، سنحسب مقياس L2 للخطأ لمثال واحد. من خط أفضل تطابق، حصلنا على القيم التالية للوزن والانحياز:
- $ \small{Weight: -4.6} $
- $ \small{Bias: 34} $
إذا توقّع النموذج أنّ سيارة تزن 2,370 رطلاً ستقطع مسافة 23.1 ميلاً لكل غالون، ولكنّها في الواقع تقطع مسافة 26 ميلاً لكل غالون، سنحسب خسارة L2 على النحو التالي:
| القيمة | معادلة | النتيجة |
|---|---|---|
| التوقّع | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| القيمة الفعلية | $ \small{ label } $ | $ \small{ 26 } $ |
| خسارة 2 | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
في هذا المثال، تبلغ قيمة L2 المفقودة لنقطة البيانات الفردية هذه 8.41.
اختيار خسارة
يعتمد قرار استخدام MAE أو MSE على مجموعة البيانات والطريقة التي تريد بها التعامل مع بعض التوقعات. عادةً ما تندرج معظم قيم الميزات في مجموعة البيانات ضمن نطاق مميّز. على سبيل المثال، يتراوح وزن السيارات عادةً بين 2000 و5000 رطل، وتستهلك ما بين 8 و50 ميلاً لكل غالون. تُعدّ السيارة التي يبلغ وزنها 8,000 رطل أو السيارة التي تقطع 100 ميل لكل غالون قيمة متطرفة لأنّها خارج النطاق المعتاد.
يمكن أن يشير الشذوذ أيضًا إلى مدى اختلاف توقّعات النموذج عن القيم الحقيقية. على سبيل المثال، يقع وزن 3,000 رطل ضمن نطاق وزن السيارة العادي، كما أنّ 40 ميلاً لكل غالون يقع ضمن نطاق كفاءة استهلاك الوقود العادي. في المقابل، ستكون السيارة التي تزن 3,000 رطل وتستهلك 40 ميلاً لكل غالون أمريكية قيمة متطرفة في ما يتعلّق بتوقّعات النموذج، لأنّ النموذج سيتوقّع أنّ السيارة التي تزن 3,000 رطل ستستهلك حوالي 20 ميلاً لكل غالون أمريكية.
عند اختيار أفضل دالة خسارة، يجب مراعاة الطريقة التي تريد أن يتعامل بها النموذج مع القيم الشاذة. على سبيل المثال، يميل MSE إلى القيم الخارجة عن النطاق الطبيعي، بينما لا يميل MAE إلى ذلك. يؤدي فقدان L2 إلى فرض عقوبة أعلى بكثير على القيمة الشاذة مقارنةً بفقدان L1. على سبيل المثال، تعرض الصور التالية نموذجًا تم تدريبه باستخدام MAE ونموذجًا تم تدريبه باستخدام MSE. يمثّل الخط الأحمر نموذجًا تم تدريبه بالكامل وسيتم استخدامه لتقديم التوقعات. تكون القيم الشاذة أقرب إلى النموذج المدرَّب باستخدام متوسط الخطأ التربيعي (MSE) مقارنةً بالنموذج المدرَّب باستخدام متوسط الخطأ المطلق (MAE).
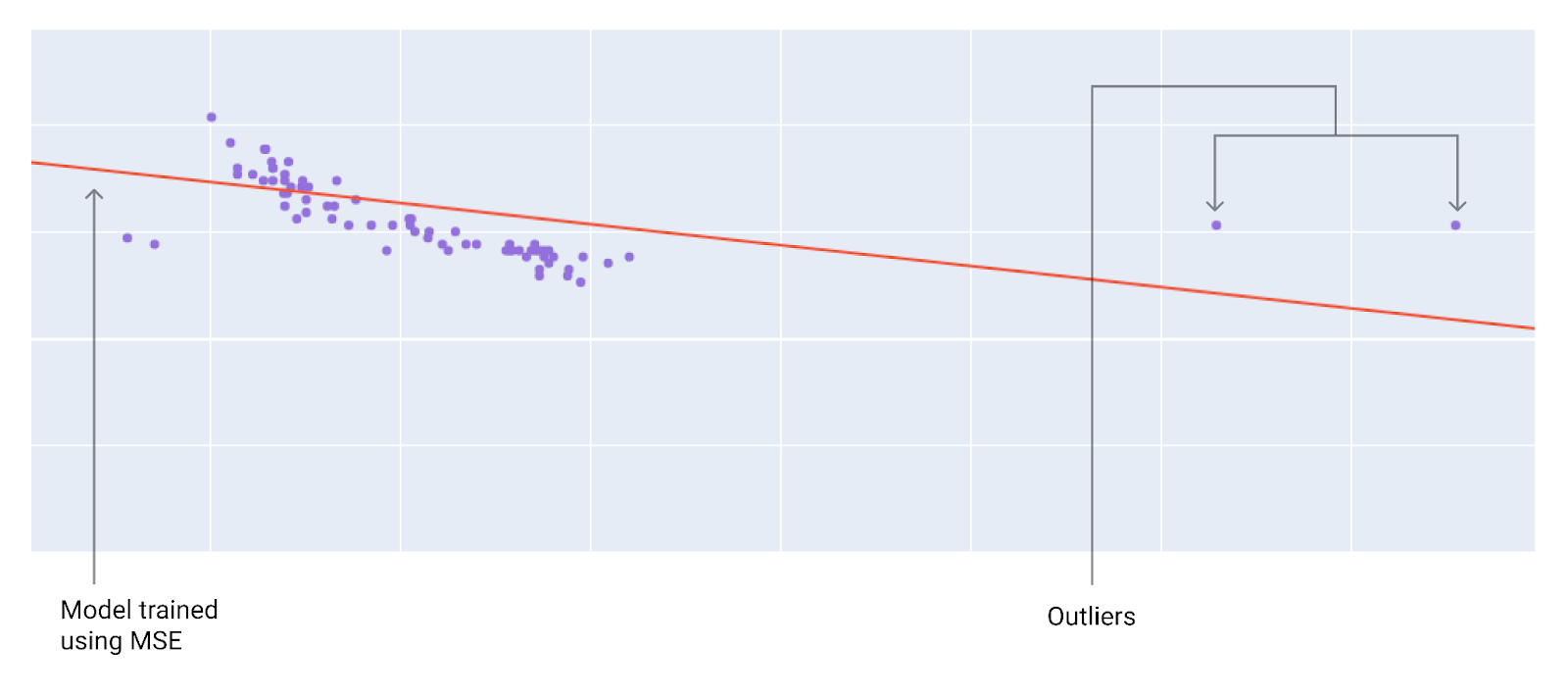
الشكل 9 يؤدي استخدام MSE في تدريب نموذج إلى تقريب النموذج من القيم الشاذة.
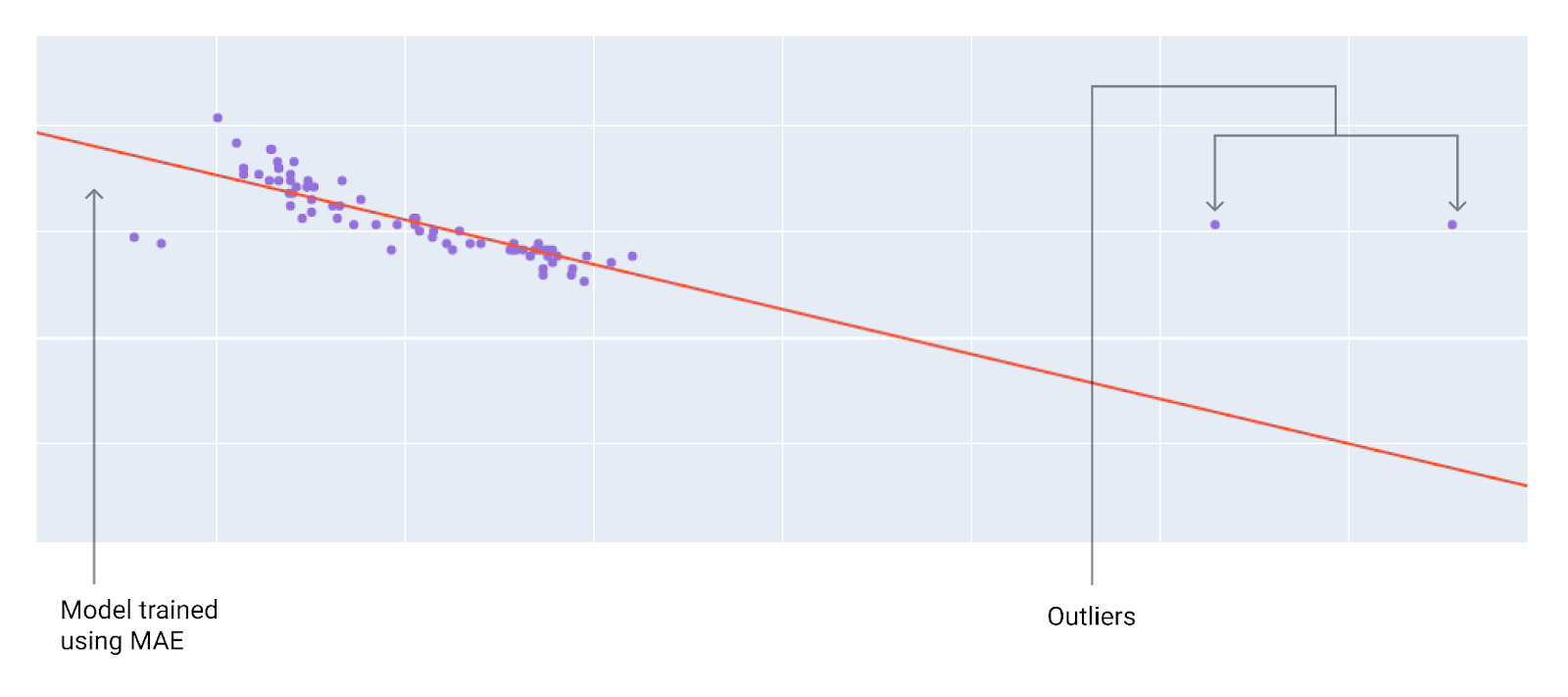
الشكل 10 يكون النموذج المدرَّب باستخدام متوسط الخطأ المطلق أبعد عن القيم الشاذة.
لاحظ العلاقة بين النموذج والبيانات:
MSE يكون النموذج أقرب إلى القيم الشاذة وأبعد عن معظم نقاط البيانات الأخرى.
MAE يكون النموذج أبعد عن القيم الشاذة ولكنه أقرب إلى معظم نقاط البيانات الأخرى.
التحقّق من فهمك
لنفترض أنّ لديك المخططَين التاليَين لنموذج خطي ملائم لمجموعة بيانات:
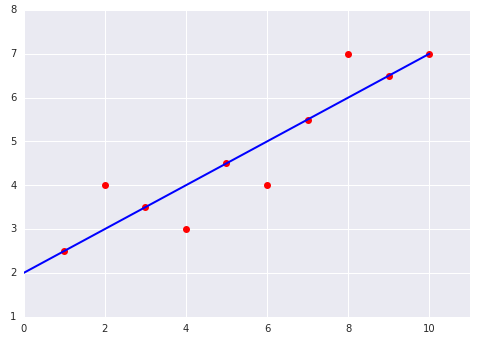
|
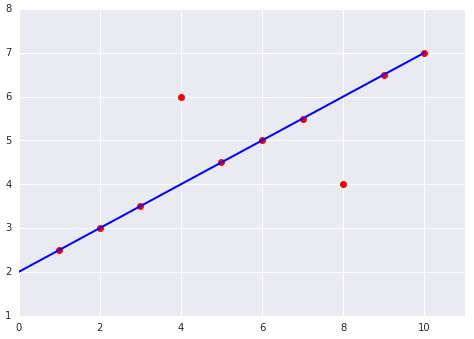
|
