損失是描述模型預測錯誤程度的數值指標。損失會測量模型預測與實際標籤之間的距離。訓練模型的目標是盡可能降低損失值。
在下圖中,您可以將損失視覺化為從資料點繪製到模型的箭頭。箭頭顯示模型預測值與實際值的差距。
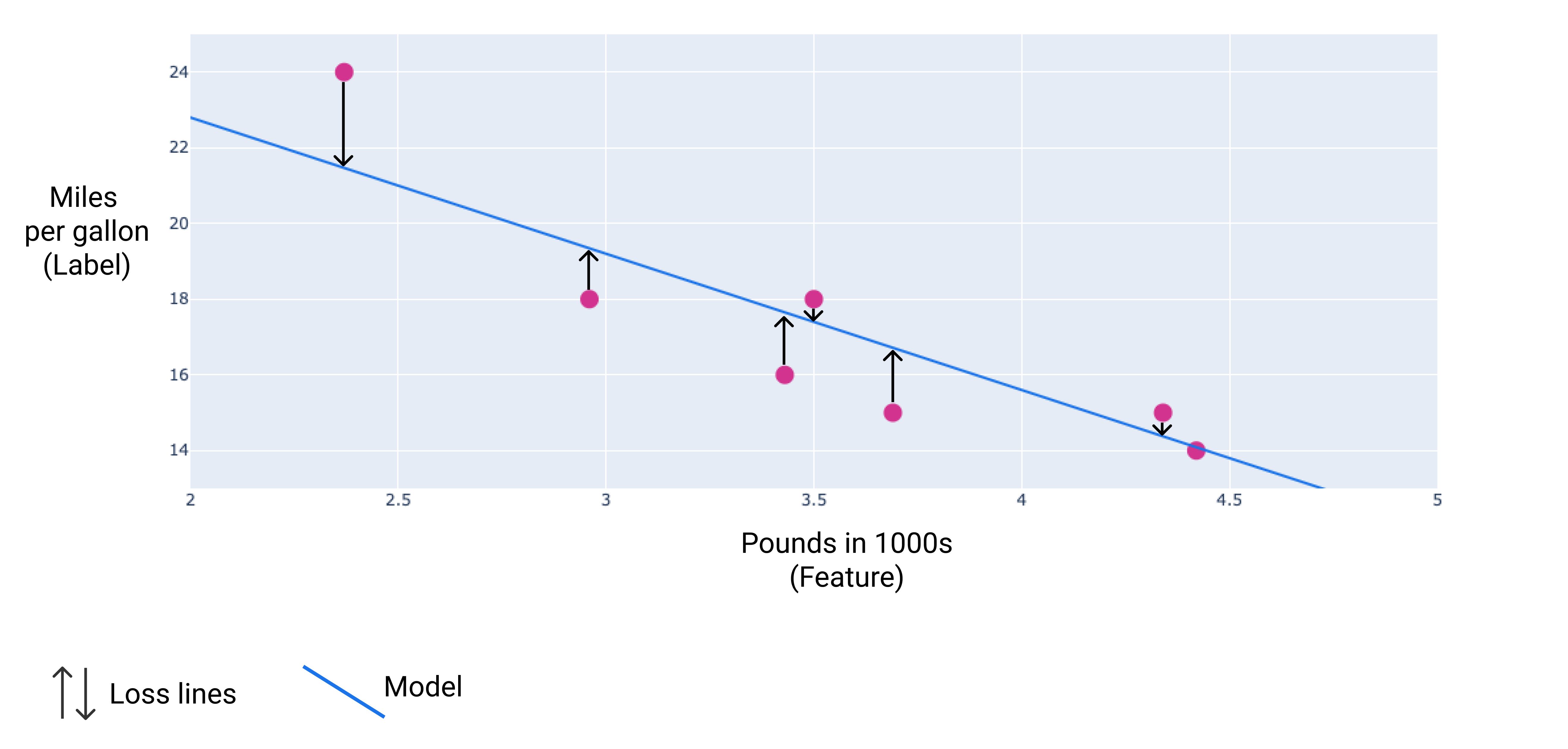
圖 8. 損失的計算方式是從實際值到預測值。
損失距離
在統計和機器學習中,損失會測量預測值和實際值之間的差異。損失著重於值之間的距離,而非方向。舉例來說,如果模型預測值為 2,但實際值為 5,我們不會在意損失為負值 ($ 2-5=-3 $)。相反地,我們會在意值之間的距離為 $ 3 $。因此,所有損失計算方法都會移除符號。
移除標記最常見的兩種方法如下:
- 計算實際值與預測值之間的絕對差異。
- 計算實際值與預測值之間的差值,然後取平方。
損失類型
在線性迴歸中,主要有五種損失類型,如下表所示。
| 損失類型 | 定義 | 方程式 |
|---|---|---|
| L1 損失 | 預測值與實際值之間差異的絕對值總和。 | $ ∑ | 實際值 - 預測值 | $ |
| 平均絕對誤差 (MAE) | 一組 N 個範例的平均 L1 損失。 | $ \frac{1}{N} ∑ | 實際值 - 預測值 | $ |
| L2 損失 | 預測值與實際值之間的平方差總和。 | $ ∑(實際值 - 預測值)^2 $ |
| 均方誤差 (MSE) | 一組 N 個範例的平均 L2 損失。 | $ \frac{1}{N} ∑ (actual\ value - predicted\ value)^2 $ |
| 均方根誤差 (RMSE) | 均方誤差 (MSE) 的平方根。 | $ \sqrt{\frac{1}{N} ∑ (actual\ value - predicted\ value)^2} $ |
L1 損失和 L2 損失 (或 MAE/RMSE 和 MSE) 之間的函數差異是平方。如果預測結果與標籤之間的差異很大,平方運算會使損失更大。如果差異很小 (小於 1),平方運算會讓損失更小。
在某些情況下,MAE 和 RMSE 等損失指標可能比 L2 損失或 MSE 更合適,因為這些指標通常更容易解讀,且會使用與模型預測值相同的比例來測量誤差。
一次處理多個樣本時,建議您無論使用 MAE、MSE 或 RMSE,都應計算所有樣本的平均損失。
計算損失範例
使用先前的最佳擬合線,我們會計算單一範例的 L2 損失。從最佳擬合線,我們得到以下權重和偏差值:
- $ \small{Weight: -4.6} $
- $ \small{Bias: 34} $
如果模型預測 2,370 磅的車輛每加侖可跑 23.1 英里,但實際每加侖可跑 26 英里,我們會按照下列方式計算 L2 損失:
| 值 | 方程式 | 結果 |
|---|---|---|
| 預測 | $\small{bias + (weight * feature\ value)}$ $\small{34 + (-4.6*2.37)}$ |
$\small{23.1}$ |
| 實際值 | $ \small{ label } $ | $ \small{ 26 } $ |
| L2 損失 | $ \small{ (actual\ value - predicted\ value)^2 } $ $\small{ (26 - 23.1)^2 }$ |
$\small{8.41}$ |
在這個例子中,該單一資料點的 L2 損失為 8.41。
選擇損失
決定使用 MAE 或 MSE 時,可考量資料集和您處理特定預測的方式。資料集中的大多數特徵值通常會落在特定範圍內。舉例來說,汽車的重量通常介於 2000 到 5000 磅,每加侖汽油可跑 8 到 50 英里。如果車輛重達 8,000 磅,或每加侖可跑 100 英里,就超出一般範圍,會被視為離群值。
離群值也可以指模型預測值與實際值之間的差距。舉例來說,3,000 磅是常見的車輛重量範圍,而每加侖 40 英里是常見的燃油效率範圍。不過,如果車輛重達 3,000 磅,每加侖可跑 40 英里,這就屬於模型預測的離群值,因為模型會預測 3,000 磅的車輛每加侖可跑約 20 英里。
選擇最佳損失函式時,請考量您希望模型如何處理離群值。舉例來說,MSE 會將模型往離群值移動,但 MAE 不會。相較於 L1 損失,L2 損失對離群值的懲罰高出許多。舉例來說,下圖顯示使用 MAE 訓練的模型,以及使用 MSE 訓練的模型。紅線代表經過完整訓練的模型,可用於進行預測。與使用 MAE 訓練的模型相比,離群值更接近使用 MSE 訓練的模型。
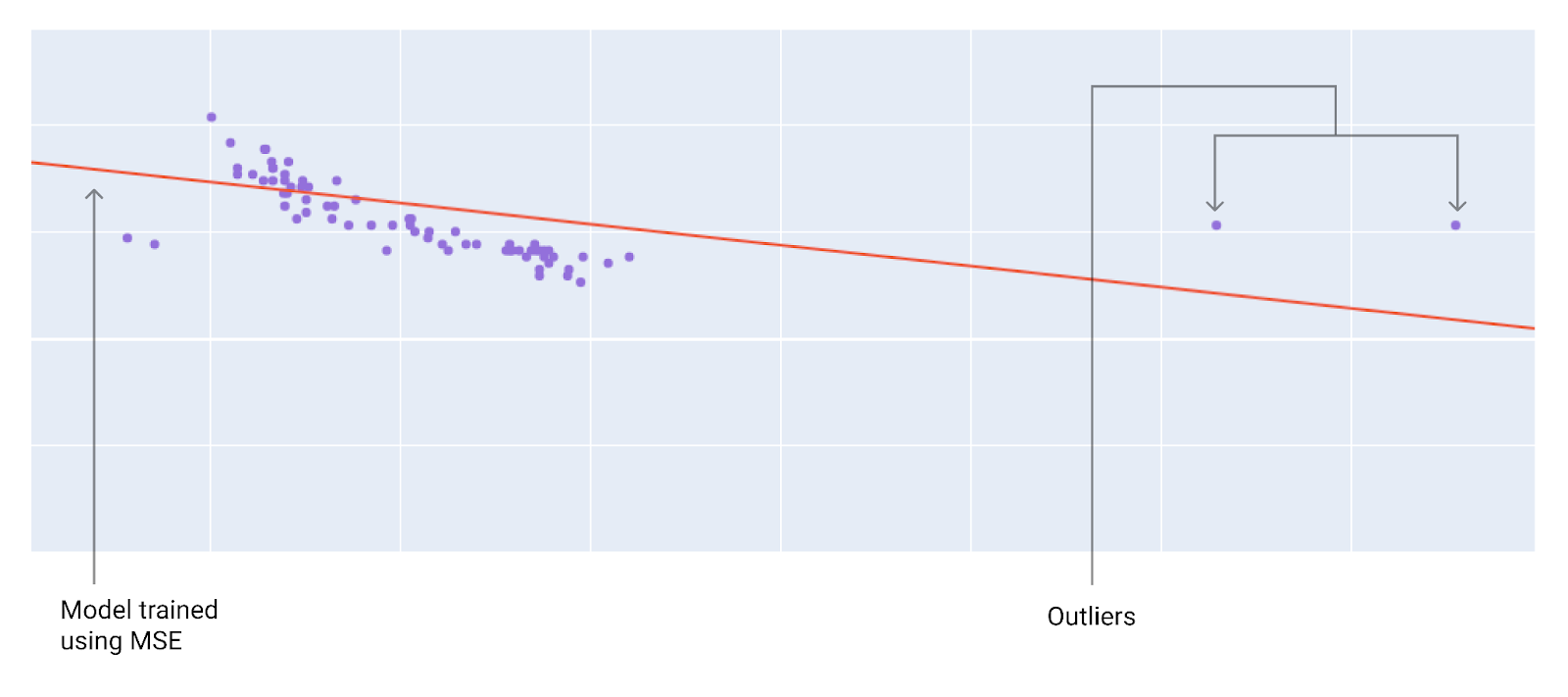
圖 9. MSE 損失會讓模型更接近離群值。
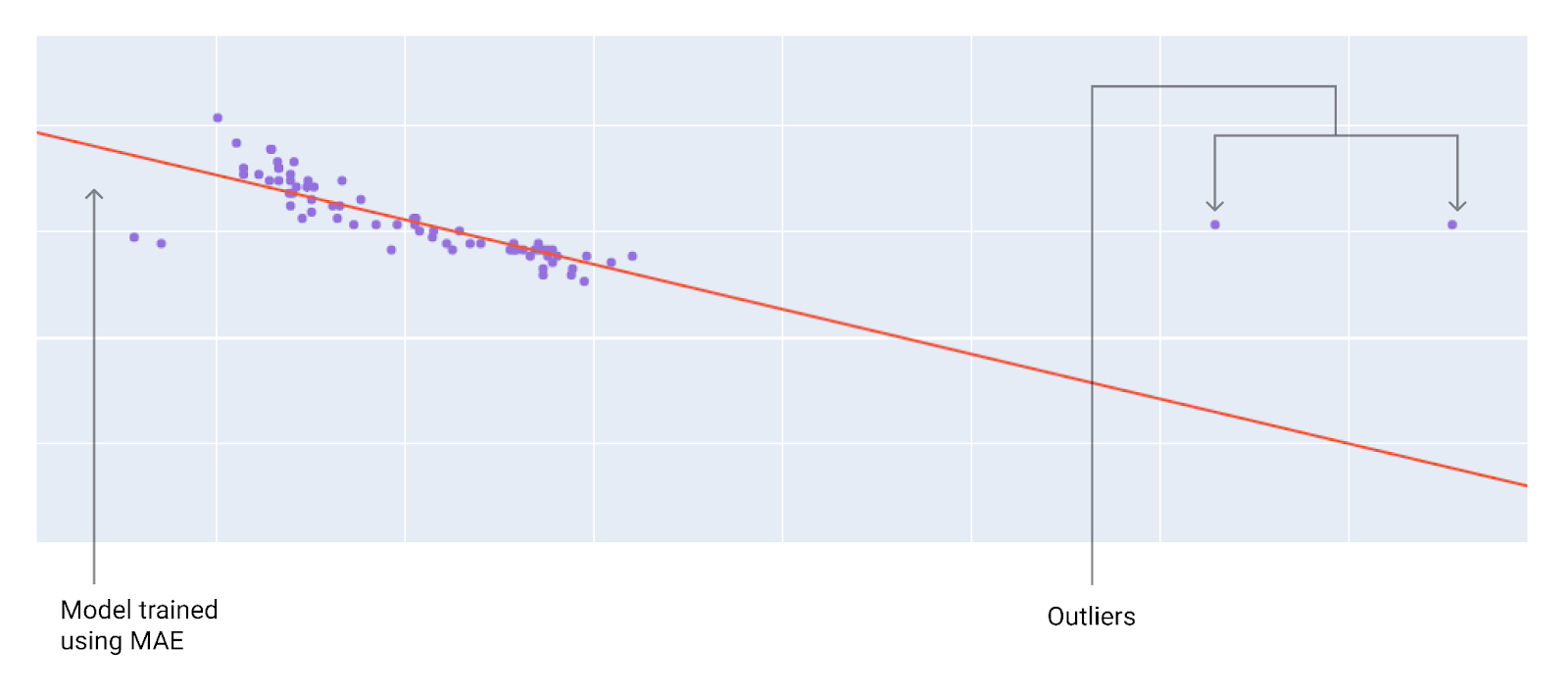
圖 10. MAE 損失可讓模型遠離離群值。
請注意模型與資料之間的關係:
MSE。模型較接近離群值,但距離大多數其他資料點較遠。
MAE。模型與離群值相距較遠,但與大多數其他資料點的距離較近。
隨堂測驗
請看以下兩個線性模型圖,這些模型適合資料集:
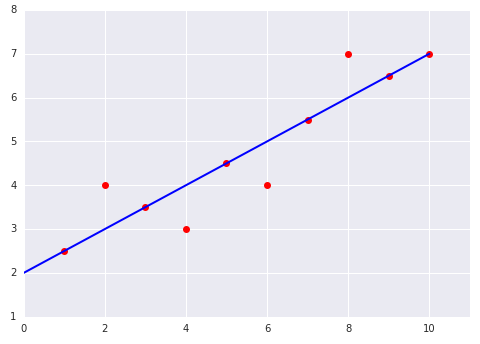
|
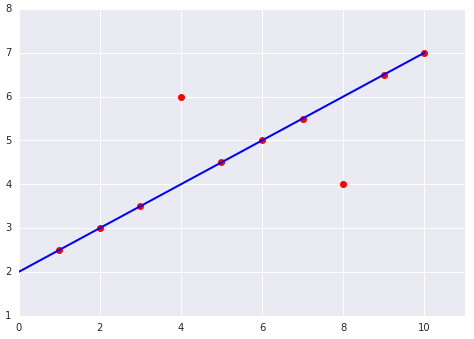
|
