Embeddings: Embedding space and static embeddings

An embedding is a vector representation of data in embedding space. Generally speaking, a model finds potential embeddings by projecting the high-dimensional space of initial data vectors into a lower-dimensional space. For a discussion of high-dimensional versus low-dimensional data, see the Categorical Data module.

Embeddings make it easier to do machine learning on large feature vectors, such as the sparse vectors representing meal items discussed in the previous section. Sometimes the relative positions of items in embedding space have a potential semantic relationship, but often the process of finding a lower-dimensional space, and relative positions in that space, is not interpretable by humans, and the resulting embeddings are difficult to understand.

Still, for the sake of human understanding, to give an idea of how embedding vectors represent information, consider the following one-dimensional representation of the dishes hot dog, pizza, salad, shawarma, and borscht, on a scale of "least like a sandwich" to "most like a sandwich." The single dimension is an imaginary measure of "sandwichness."

Figure 3. Foods along an imagined dimension of "sandwichness."

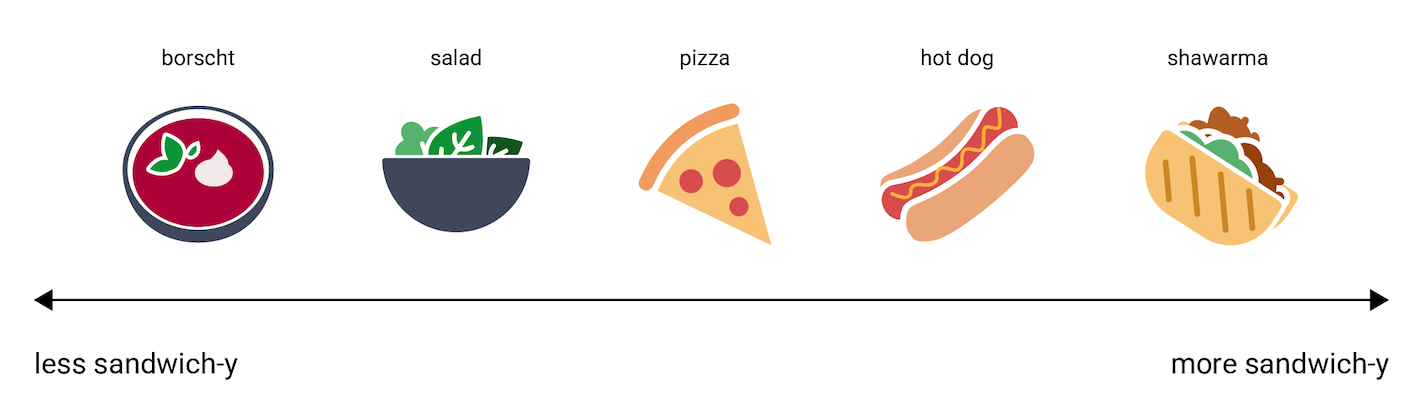
Where on this line would an apple strudel fall? Arguably, it could be placed between hot dog and shawarma. But apple strudel also seems to have an additional dimension of sweetness or dessertness that makes it very different from the other options. The following figure visualizes this by adding a "dessertness" dimension:

Figure 4. Foods plotted by both "sandwichness" and "dessertness."

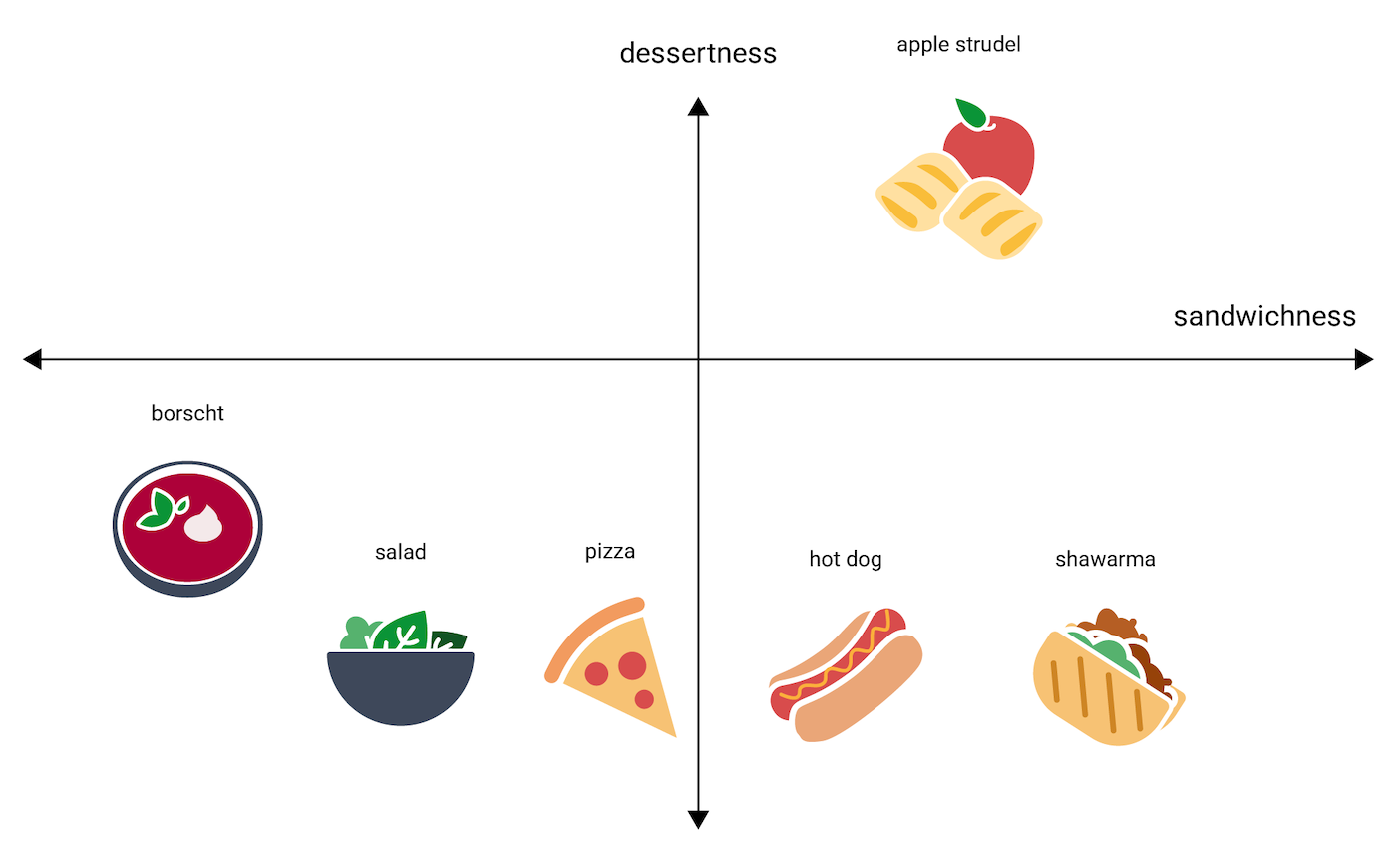
An embedding represents each item in n-dimensional space with n floating-point numbers (typically in the range –1 to 1 or 0 to 1). The embedding in Figure 3 represents each food in one-dimensional space with a single coordinate, while Figure 4 represents each food in two-dimensional space with two coordinates. In Figure 4, "apple strudel" is in the upper-right quadrant of the graph and could be assigned the point (0.5, 0.3), whereas "hot dog" is in the bottom-right quadrant of the graph and could be assigned the point (0.2, –0.5).

In an embedding, the distance between any two items can be calculated mathematically, and can be interpreted as a measure of relative similarity between those two items. Two things that are close to each other, like shawarma and hot dog in Figure 4, are more closely related in the model's representation of the data than two things more distant from each other, like apple strudel and borscht.

To learn about different methods of calculating distance between embedding vectors, see Measuring Similarity from Embeddings.

Notice also that in the 2D space in Figure 4, apple strudel is much farther from shawarma and hot dog than it would be in the 1D space, which matches intuition: apple strudel is not as similar to a hot dog or a shawarma as hot dogs and shawarmas are to each other.

Now consider borscht, which is much more liquid than the other items. This suggests a third dimension, liquidness, or how liquid a food might be. Adding that dimension, the items could be visualized in 3D in this way:

Figure 5. Foods plotted by "sandwichness," "dessertness," and "liquidness."

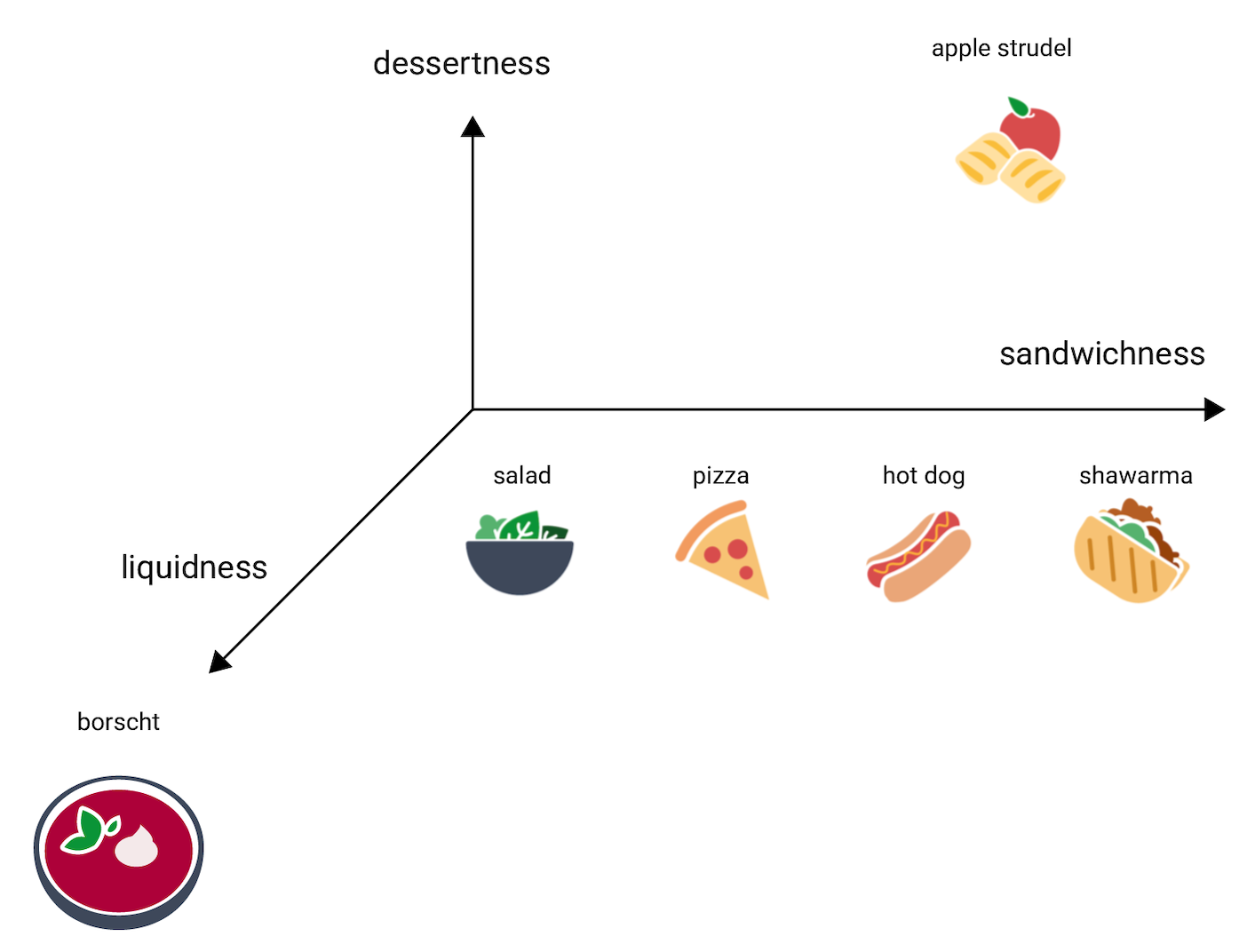
Where in this 3D space would tangyuan go? It's soupy, like borscht, and a sweet dessert, like apple strudel, and most definitely not a sandwich. Here is one possible placement:

Figure 6. Adding tangyuan to the previous image, high on "dessertness" and "liquidness" and low on "sandwichness."

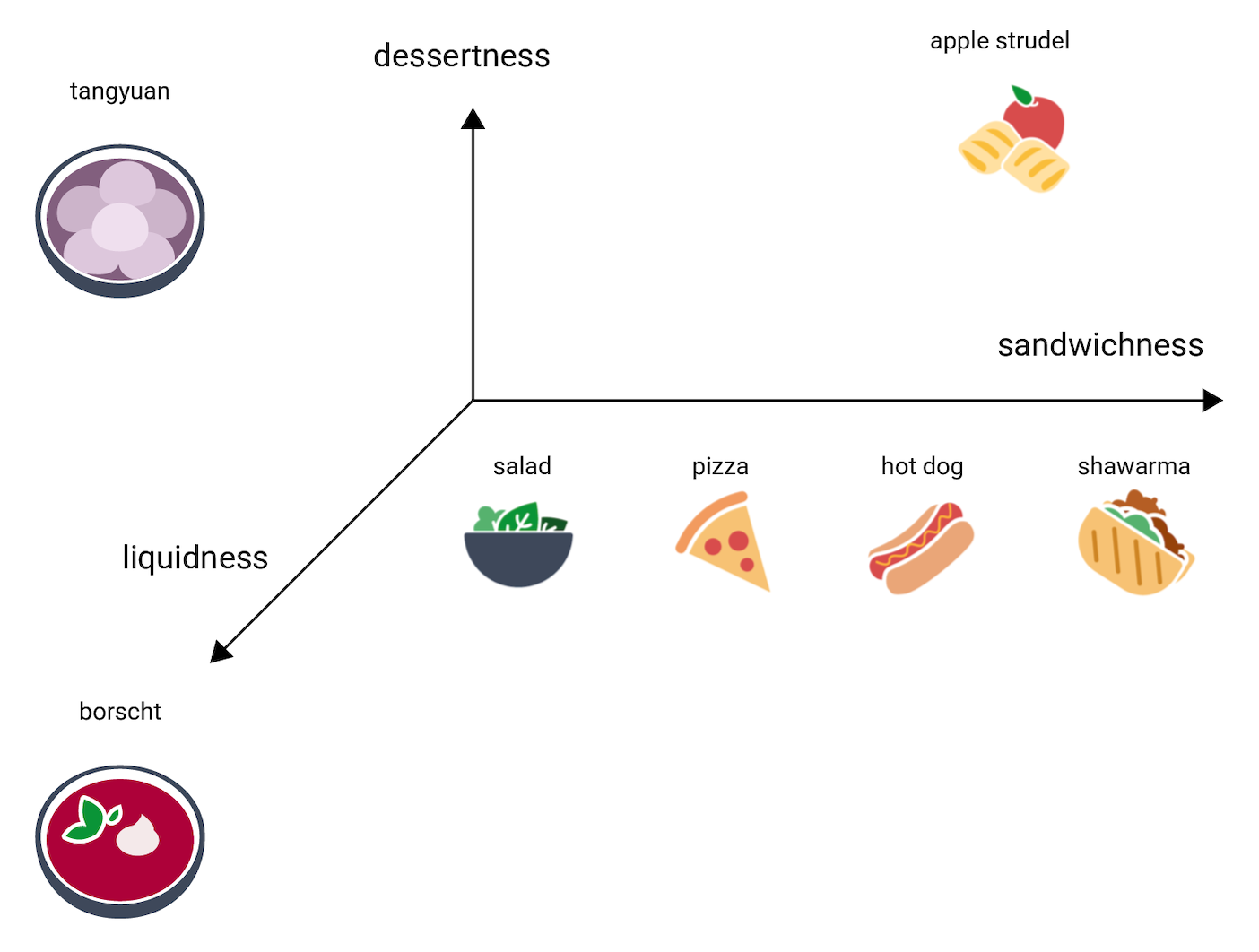
Notice how much information is expressed in these three dimensions. You could imagine adding additional dimensions, like how meaty or baked a food might be, though 4D, 5D, and higher-dimensional spaces are difficult to visualize.

Real-world embedding spaces

In the real world, embedding spaces are d-dimensional, where d is much higher than 3, though lower than the dimensionality of the data, and relationships between data points are not necessarily as intuitive as in the contrived illustration above. (For word embeddings, d is often 256, 512, or 1024.¹)

In practice, the ML practitioner usually sets the specific task and the number of embedding dimensions. The model then tries to arrange the training examples to be close in an embedding space with the specified number of dimensions, or tunes for the number of dimensions, if d is not fixed. The individual dimensions are rarely as understandable as "dessertness" or "liquidness." Sometimes what they "mean" can be inferred but this is not always the case.

Embeddings will usually be specific to the task, and differ from each other when the task differs. For example, the embeddings generated by a vegetarian versus non-vegetarian classification model will be different from the embeddings generated by a model that suggests dishes based on time of day or season. "Cereal" and "breakfast sausage" would probably be close together in the embedding space of a time-of-day model but far apart in the embedding space of a vegetarian versus non-vegetarian model, for example.

Static embeddings

While embeddings differ from task to task, one task has some general applicability: predicting the context of a word. Models trained to predict the context of a word assume that words appearing in similar contexts are semantically related. For example, training data that includes the sentences "They rode a burro down into the Grand Canyon" and "They rode a horse down into the canyon" suggests that "horse" appears in similar contexts to "burro." It turns out that embeddings based on semantic similarity work well for many general language tasks.

While it's an older example, and largely superseded by other models, the word2vec model remains useful for illustration. word2vec trains on a corpus of documents to obtain a single global embedding per word. When each word or data point has a single embedding vector, this is called a static embedding. The following video walks through a simplified illustration of word2vec training.

Note: word2vec can refer to both an algorithm for obtaining static word embeddings and a set of word vectors that were pretrained with that algorithm. It's used in both senses in this module.

Research suggests that these static embeddings, once trained, encode some degree of semantic information, particularly in relationships between words. That is, words that are used in similar contexts will be closer to each other in embedding space. The specific embeddings vectors generated will depend on the corpus used for training. See T. Mikolov et al (2013), "Efficient estimation of word representations in vector space", for details.

The following exercises use TensorFlow's Embedding Projector, set to Word2Vec 10k in the Data section of the left sidebar, which should be the default selection. This visualization flattens 10,000 word2vec static vectors into a 3D space. Collapsing dimensions in this way can be misleading, because the points closest to each other in the original high-dimensional space may appear farther apart in the 3D projection.

Click the rotating visualization to pause it.

In the right sidebar, you can search for a specific word in Search, set to by: word. For any search with multiple results, click the text of the word to show the word's n nearest neighbors and their distances to your target word. (Use either distance calculation). You can set n either by dragging the slider or typing in the box to the right of neighbors.

If you search for the first word in the first exercise below, then click the text of iii, the right sidebar should look like this:

Figure 7. The nearest 20 neighbors of iii in the Embedding Projector.

Note: To show nearest neighbors on any search with multiple results, you must click the letters of the target word, and not the whitespace to either side.

Exercise

In these experiments, you'll play with the word2vec embeddings in Tensorflow's Embedding Projector.

Task 1

Try to find the 20 nearest neighbors for the following, and see where the groups fall in the cloud.

• iii, third, and three
• tao and way
• orange, yellow, and juice

What do you notice about these results?

Click here for our answer

Even though iii, third, and three are semantically similar, they appear in different contexts in text and don't appear to be close together in this embedding space. In word2vec, iii is closer to iv than to third.

Similarly, while way is a direct translation of tao, these words most frequently occur with completely different groups of words in the dataset used, and so the two vectors are very far apart.

The first several nearest neighbors of orange are colors, but juice and peel, related to the meaning of orange as fruit, show up as the 14th and 18th nearest neighbors. prince, meanwhile, as in the Prince of Orange, is 17th. In the projection, the words closest to orange are yellow and other colors, while the closest words to juice don't include orange.

Task 2

Try to figure out some characteristics of the training data. For example, try to find the 100 nearest neighbors for the following, and see where the groups are in the cloud:

• boston, paris, tokyo, delhi, moscow, and seoul (this is a trick question)
• jane, sarah, john, peter, rosa, and juan

Click here for our answer

Many of the nearest neighbors to boston are other cities in the US. Many of the nearest neighbors to paris are other cities in Europe. tokyo and delhi don't seem to have similar results: one is associated with cities around the world that are travel hubs, while the other is associated with india and related words. seoul doesn't appear in this trimmed-down set of word vectors at all.

It seems that this dataset contains many documents related to US national geography, some documents relate to European regional geography, and not much fine-grained coverage of other countries or regions.

Similarly, this dataset seems to contain many male English names, some female English names, and far fewer names from other languages. Note that Don Rosa wrote and illustrated Scrooge McDuck comics for Disney, which is the likely reason that `scrooge` and `mcduck` are among the nearest neighbors for `rosa`.

The pre-trained word vectors offered by word2vec were in fact trained on Google News articles up to 2013.

Task 3

Embeddings aren't limited to words. Images, audio, and other data can also be embedded. For this task:

1. Open TensorFlow's Embedding Projector.
2. In the left sidebar titled Data, choose Mnist with images. This brings up a projection of the embeddings of the MNIST database of handwritten digits.
3. Click to stop the rotation and choose a single image. Zoom in and out as needed.
4. Look in the right sidebar for nearest neighbors. Are there any surprises?

• Why do some 7s have 1s as their nearest neighbor? Why do some 8s have 9 as their nearest neighbor?
• Is there anything about the images on the edges of the projection space that seem different from the images in the center of the projection space?

Keep in mind that the model that created these embeddings is receiving image data, which is to say, pixels, and choosing a numerical vector representation for each image. The model doesn't make an automatic mental association between the image of the handwritten digit and the numerical digit itself.

Click here for our answer

Due to similarities in shape, the vector representations of some of the skinnier, narrower 7s are placed closer to the vectors for handwritten 1s. The same thing happens for some 8s and 9s, and even some of the 5s and 3s.

The handwritten digits on the outside of the projection space appear more strongly definable as one of the nine digits and strongly differentiated from other possible digits.

Key terms:

• Embedding vector
• Embedding space

---

1. François Chollet, Deep Learning with Python (Shelter Island, NY: Manning, 2017), 6.1.2. ↩