嵌入是嵌入空间中数据的向量表示法。一般来说,模型通过将初始数据向量的高维空间投影到低维空间来查找潜在的嵌入。如需了解高维数据与低维数据的不同之处,请参阅类别数据模块。
借助嵌入,我们可以更轻松地对大型特征向量(例如上一节中讨论的代表食物的稀疏向量)进行机器学习。有时,嵌入空间中各项内容的相对位置可能存在语义关系,但通常情况下,人类无法解释寻找低维空间以及该空间中的相对位置的过程,并且生成的嵌入很难理解。
不过,为了便于理解,并了解嵌入向量如何表示信息,请看看以下对菜肴热狗、披萨、沙拉、沙瓦玛和罗宋汤的一维表示法,从“最不像三明治”到“最像三明治”进行评分。单个维度是“三明治度”的虚构衡量标准。
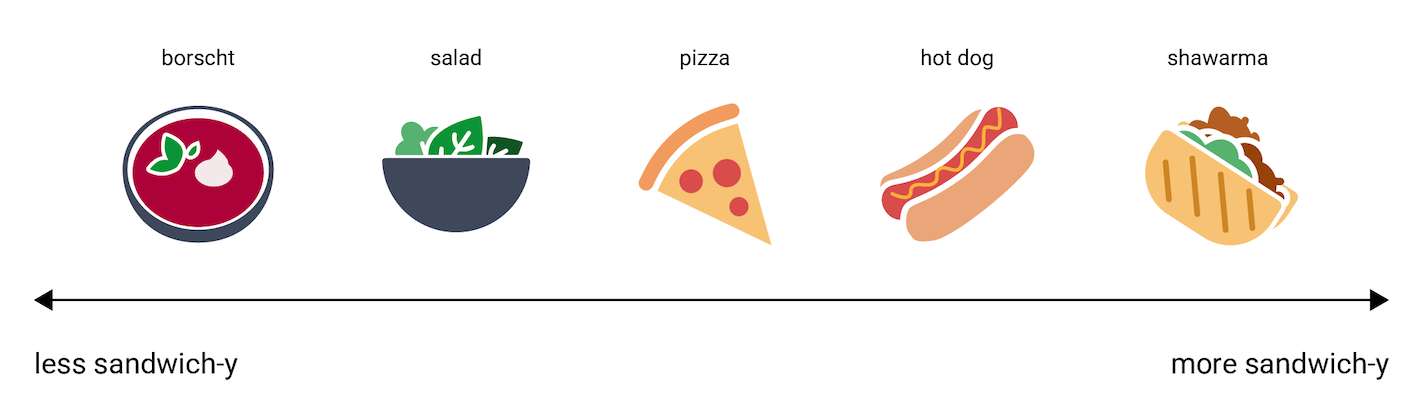
苹果馅饼会落在哪个位置?可以将其放置在 hot dog 和 shawarma 之间。但苹果馅饼似乎还具有额外的甜度或甜点度维度,这使其与其他选项大不相同。下图通过添加“甜点度”维度来直观呈现这一点:
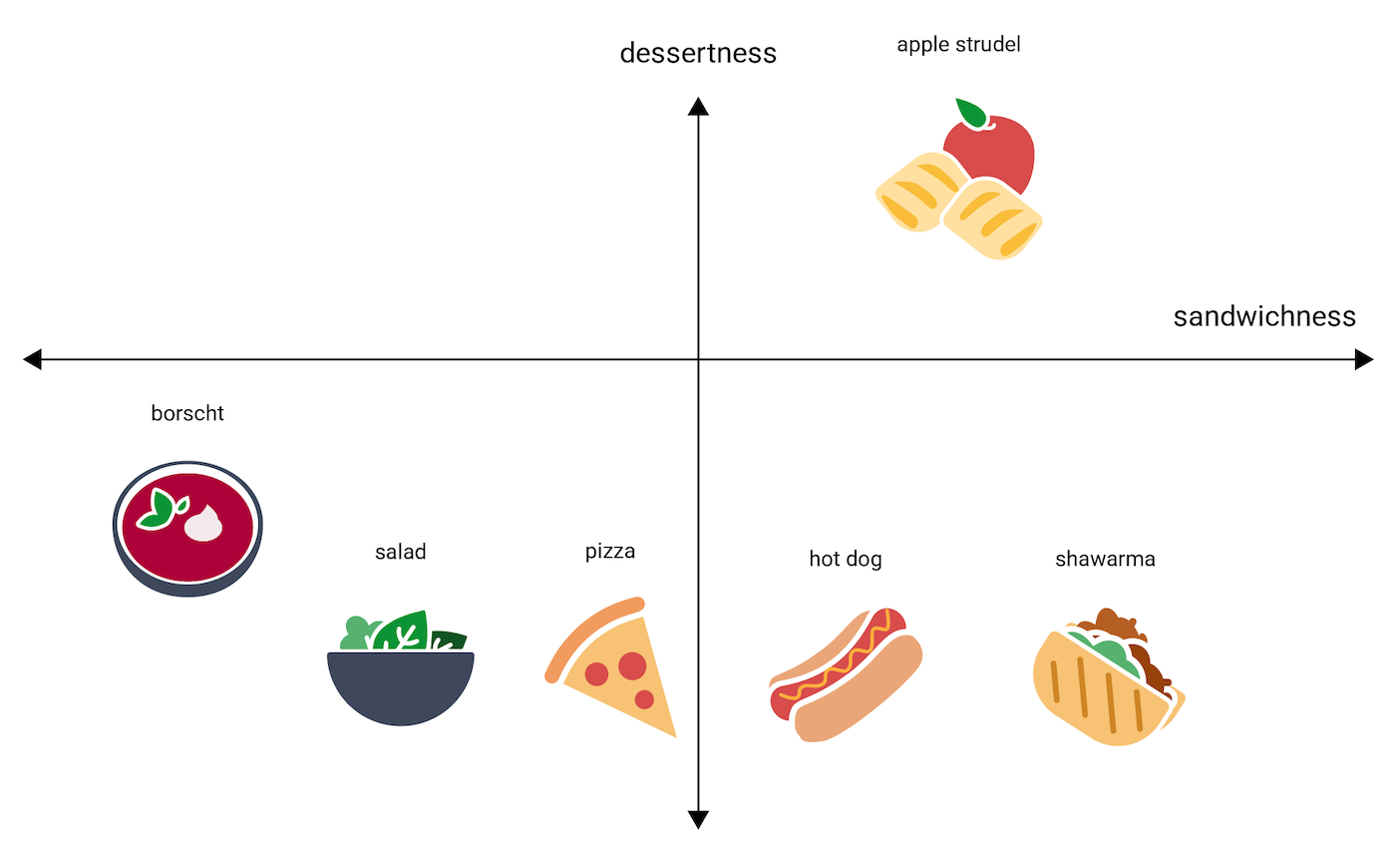
嵌入式表示法使用 n 个浮点数(通常介于 –1 到 1 或 0 到 1 之间)来表示 n 维空间中的每个项。图 3 中的嵌入表示在单维空间中使用单个坐标表示每种食物,而图 4 表示在二维空间中使用两个坐标表示每种食物。在图 4 中,“苹果馅饼”位于图表的右上象限,可以分配点 (0.5, 0.3),而“热狗”位于图表的右下象限,可以分配点 (0.2, –0.5)。
在嵌入中,可以通过数学方式计算任意两项之间的距离,并将其解释为衡量这两项之间相似程度的指标。彼此靠近的两项(例如图 4 中的 shawarma 和 hot dog)在模型的数据表示法中比彼此较远的两项(例如 apple strudel 和 borscht)更密切相关。
另请注意,在图 4 中的 2D 空间中,apple strudel 与 shawarma 和 hot dog 的距离比在 1D 空间中更远,这符合直觉:apple strudel 与热狗或沙瓦玛之间的相似度不如热狗与沙瓦玛之间的相似度。
现在,考虑一下罗宋汤,它比其他菜肴含有更多的液体。这暗示了第三个维度,即液体度,或者说食物的液体程度。添加该维度后,可通过以下方式以 3D 形式直观呈现食物:
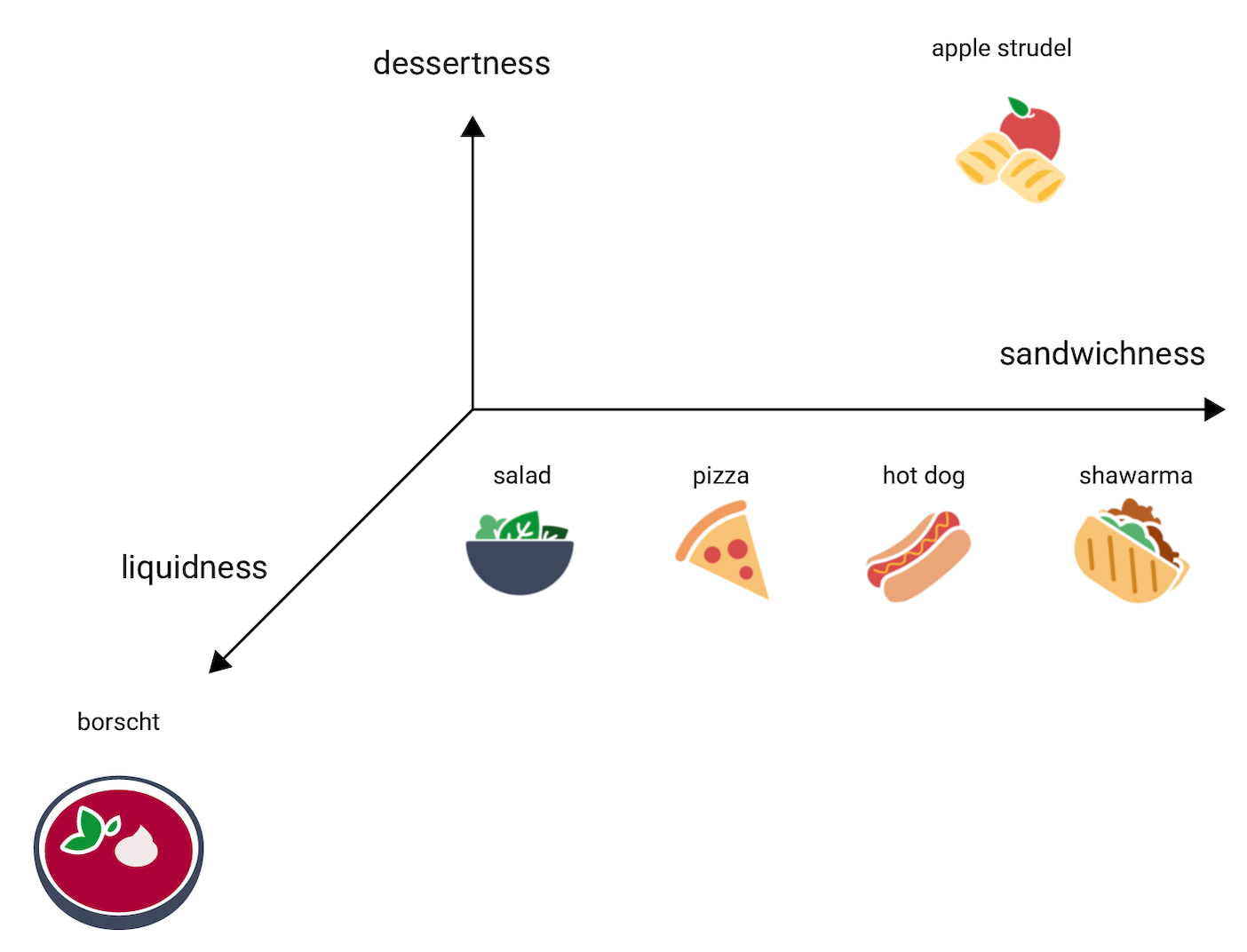
在这个 3D 空间中,汤圆会放在哪里?它是汤状的,像罗宋汤,还是甜点,像苹果馅饼,但绝对不是三明治。以下是一种可能的放置位置:

请注意这三个维度表达了多少信息。 您可以想象一下添加其他维度,例如食物的肉质或烘烤程度,但 4D、5D 和更高维空间很难直观呈现。
真实世界的嵌入空间
在现实世界中,嵌入空间是 d 维的,其中 d 远高于 3,但低于数据的维数,并且数据点之间的关系不一定像上文中所示的人工构造的图示那样直观。(对于词嵌入,d 通常为 256、512 或 1024。1)
在实践中,机器学习从业者通常会设置特定任务和嵌入维度数量。然后,模型会尝试将训练样本安排在具有指定维度数的嵌入空间中,或者自动适配最佳维度数量(如果 d 未固定)。具体维度很少像“甜点度”或“液体度”那样易于理解。有时,可以推断出它们的“含义”,但并非总是如此。
嵌入通常因任务而异,并且在任务不同时也会有所不同。例如,素食与非素食分类模型生成的嵌入将不同于根据时间或季节建议菜肴的模型生成的嵌入。例如,“Cereal”和“breakfast sausage”在一天时段模型的嵌入空间中可能相距不远,但在素食与非素食模型的嵌入空间中可能相距甚远。
静态嵌入
虽然不同任务的嵌入各不相同,但有一个任务具有一定的通用适用性:预测字词的上下文。经过训练以预测字词上下文的模型会假定在类似上下文中出现的字词在语义上是相关的。例如,包含“They rode a burro down into the Grand Canyon”和“They rode a horse down into the canyon”这两句话的训练数据表明,“horse”出现在与“burro”类似的上下文中。事实证明,基于语义相似性的嵌入对于许多常规语言任务都非常有效。
虽然 word2vec 模型是一个较旧的示例,并且已被其他模型大大取代,但它仍然可以拿出来作为示例进行说明。word2vec 会针对文档语料库进行训练,以便为每个字词获得单个全局嵌入。如果每个字词或数据点都有一个嵌入向量,则称为静态嵌入。以下视频简要介绍了 word2vec 训练。
研究表明,这些静态嵌入经过训练后会编码一定程度的语义信息,尤其是字词之间的关系。也就是说,在类似上下文中使用的字词在嵌入空间中彼此靠得更近。生成的特定嵌入向量取决于用于训练的语料库。详情请参阅 T. Mikolov 等人 (2013) 的“在向量空间中高效估算字词表示法”。
-
François Chollet,使用 Python 进行深度学习(纽约州谢尔特岛:Manning,2017 年),6.1.2。 ↩