AI-generated Key Takeaways
-
Counterfactual fairness is a metric that evaluates fairness by comparing predictions for similar individuals, differing only in a sensitive attribute like demographic group.
-
This metric is particularly useful when datasets lack complete demographic information for all examples but contain it for a subset.
-
While counterfactual fairness can identify individual-level biases, it might not address broader, systemic biases across subgroups.
-
Other fairness metrics, such as demographic parity and equality of opportunity, provide a more holistic view but may require complete demographic data.
-
Selecting the appropriate fairness metric depends on the specific application and desired outcome, with no single "right" metric universally applicable.
Thus far, our discussions of fairness metrics have assumed that our training and test examples contain comprehensive demographic data for the demographic subgroups being evaluated. But often this isn't the case.
Suppose our admissions dataset doesn't contain complete demographic data. Instead, demographic-group membership is recorded for just a small percentage of examples, such as students who opted to self-identify which group they belonged to. In this case, the breakdown of our candidate pool into accepted and rejected students now looks like this:
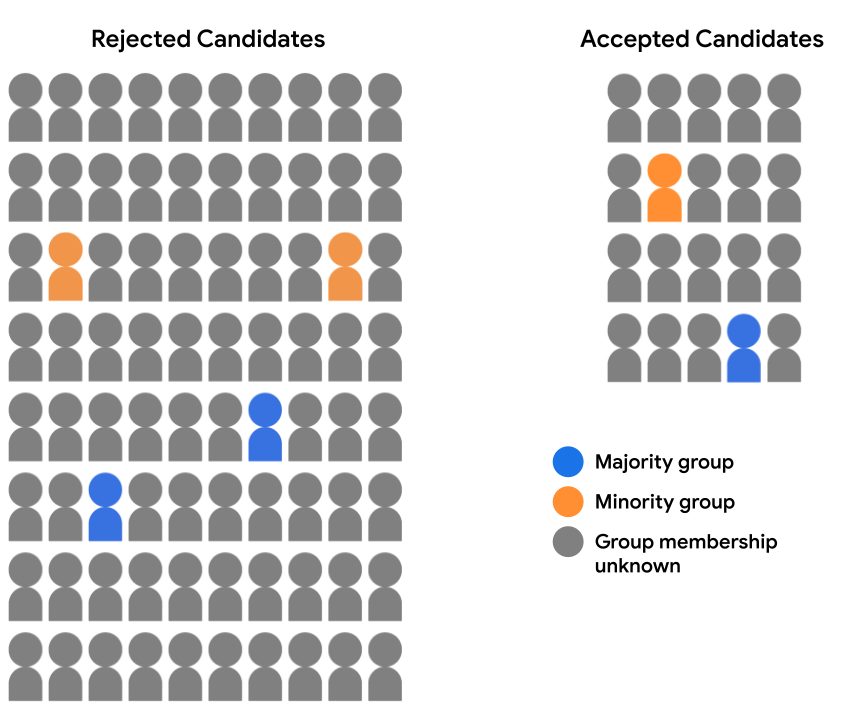
It's not feasible here to evaluate model predictions for either demographic parity or equality of opportunity, because we don't have demographic data for 94% of our examples. However, for the 6% of examples that do contain demographic features, we can still compare pairs of individual predictions (a majority candidate vs. a minority candidate) and see if they have been treated equitably by the model.
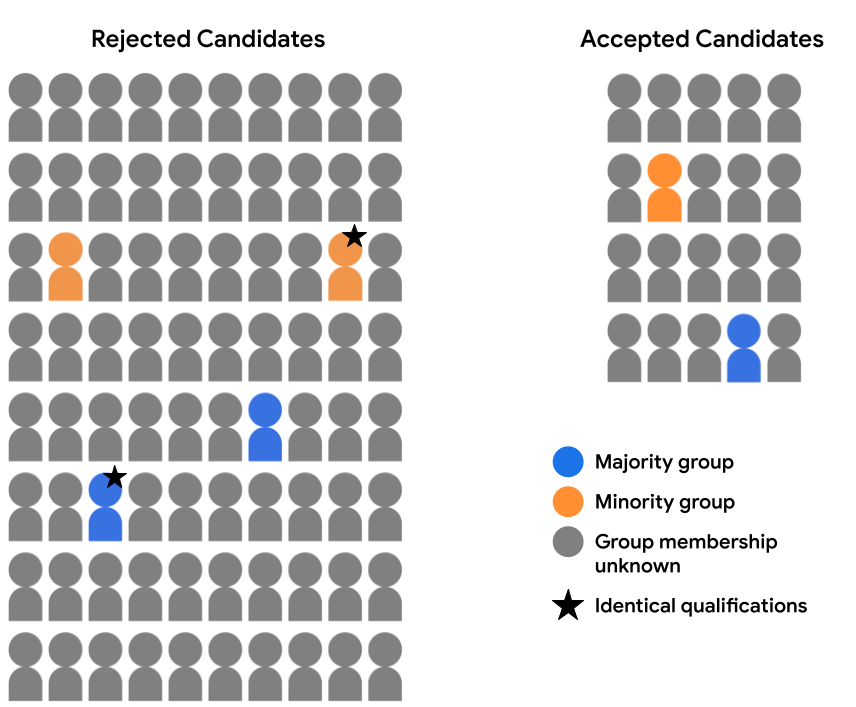
For example, let's say that we've thoroughly reviewed the feature data available for two candidates (one in the majority group and one in the minority group, annotated with a star in the image below), and have determined that they are identically qualified for admission in all respects. If the model makes the same prediction for both of these candidates (i.e., either rejects both candidates or accepts both candidates), it is said to satisfy counterfactual fairness for these examples. Counterfactual fairness stipulates that two examples that are identical in all respects, except a given sensitive attribute (here, demographic group membership), should result in the same model prediction.
Benefits and drawbacks
As mentioned earlier, one key benefit of counterfactual fairness is that it can be used to evaluate predictions for fairness in many cases where using other metrics wouldn't be feasible. If a dataset doesn't contain a full set of feature values for the relevant group attributes under consideration, it won't be possible to evaluate fairness using demographic parity or equality of opportunity. However, if these group attributes are available for a subset of examples, and it's possible to identify comparable pairs of equivalent examples in different groups, practitioners can use counterfactual fairness as a metric to probe the model for potential biases in predictions.
Additionally, because metrics like demographic parity and equality of opportunity assess groups in aggregate, they may mask bias issues that affect the model at the level of individual predictions, which can be surfaced by evaluation using counterfactual fairness. For example, suppose our admissions model accepts qualified candidates from the majority group and the minority group in the same proportion, but the most qualified minority candidate is rejected whereas the most qualified majority candidate who has the exact same credentials is accepted. A counterfactual fairness analysis can help identify these sorts of discrepancies so that they can be addressed.
On the flipside, the key downside of counterfactual fairness is that it doesn't provide as holistic a view of bias in model predictions. Identifying and remediating a handful of inequities in pairs of examples may not be sufficient to address systemic bias issues that affect entire subgroups of examples.
In cases where it's possible, practitioners can consider doing both an aggregate fairness analysis (using a metric like demographic parity or equality of opportunity) as well as a counterfactual fairness analysis to gain the widest range of insights into potential bias issues in need of remediation.
Exercise: Check your understanding
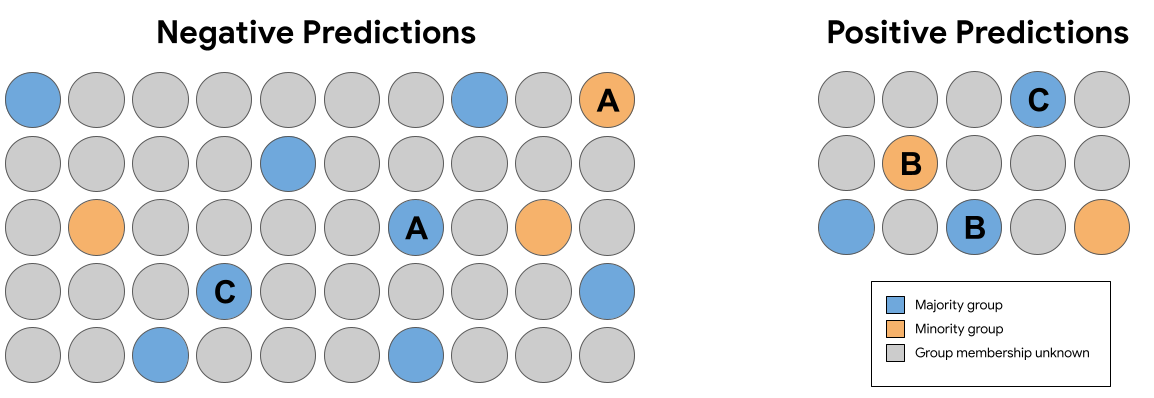
In the set of predictions in Figure 7 above, which of the following pairs of identical (excluding group membership) examples received predictions that violate counterfactual fairness?
Summary
Demographic parity, equality of opportunity, and counterfactual fairness each provide different mathematical definitions of fairness for model predictions. And those are just three possible ways to quantify fairness. Some definitions of fairness are even mutually incompatible, meaning it may be impossible to satisfy them simultaneously for a given model's predictions.
So how do you choose the "right" fairness metric for your model? You need to consider the context in which it's being used and the overarching goals you want to accomplish. For example, is the goal to achieve equal representation (in this case, demographic parity may be the optimal metric) or is it to achieve equal opportunity (here, equality of opportunity may be the best metric)?
To learn more about ML Fairness and explore these issues in more depth, see Fairness and Machine Learning: Limitations and Opportunities by Solon Barocas, Moritz Hardt, and Arvind Narayanan.