ন্যায্যতা: বিপরীত ন্যায্যতা

এই পর্যন্ত, ন্যায্যতা মেট্রিক্সের আমাদের আলোচনা অনুমান করেছে যে আমাদের প্রশিক্ষণ এবং পরীক্ষার উদাহরণগুলিতে মূল্যায়ন করা জনসংখ্যার উপগোষ্ঠীগুলির জন্য ব্যাপক জনসংখ্যার তথ্য রয়েছে৷ কিন্তু প্রায়ই এটা হয় না।

ধরুন আমাদের ভর্তির ডেটাসেটে সম্পূর্ণ ডেমোগ্রাফিক ডেটা নেই। পরিবর্তে, ডেমোগ্রাফিক-গ্রুপ সদস্যতা শুধুমাত্র একটি ছোট শতাংশ উদাহরণের জন্য রেকর্ড করা হয়, যেমন ছাত্র যারা স্ব-পরিচয় বেছে নিয়েছে তারা কোন গোষ্ঠীর অন্তর্ভুক্ত। এই ক্ষেত্রে, গৃহীত এবং প্রত্যাখ্যাত শিক্ষার্থীদের মধ্যে আমাদের প্রার্থীর পুলের ভাঙ্গন এখন এইরকম দেখাচ্ছে:

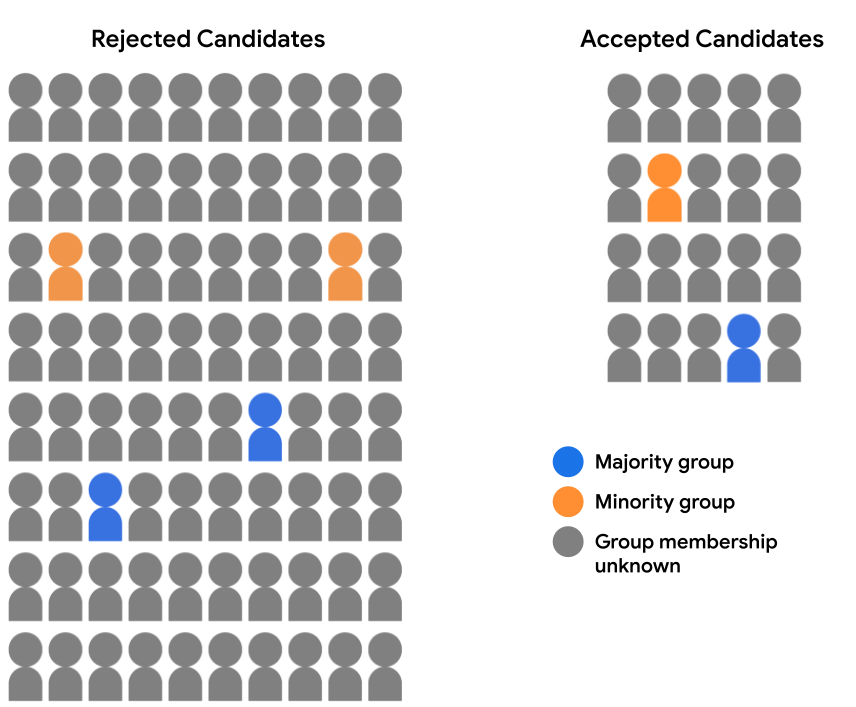
100 জন শিক্ষার্থীর একটি প্রার্থী পুল, দুটি গ্রুপে বিভক্ত: প্রত্যাখ্যাত প্রার্থী (80 ছাত্র আইকন) এবং গৃহীত প্রার্থী (20 ছাত্র আইকন)। 6টি আইকন ব্যতীত সমস্ত আইকন ধূসর ছায়াযুক্ত (তাদের জনসংখ্যার গোষ্ঠী অজানা তা নির্দেশ করে)। প্রত্যাখ্যাত গ্রুপে, দুটি ছাত্র আইকন ছায়াযুক্ত নীল এবং দুটি ছাত্র আইকন কমলা ছায়াযুক্ত। গৃহীত গ্রুপে, একটি ছাত্র আইকন ছায়াযুক্ত নীল এবং একটি কমলা ছায়াময়।
চিত্র 5. প্রার্থীর পুল, প্রায় সমস্ত প্রার্থীর জন্য জনসংখ্যাগত-গ্রুপ সদস্যতা অজানা (আইকন ধূসর ছায়ায়)।

এখানে ডেমোগ্রাফিক প্যারিটি বা সুযোগের সমতার জন্য মডেল ভবিষ্যদ্বাণী মূল্যায়ন করা সম্ভব নয়, কারণ আমাদের 94% উদাহরণের জন্য জনসংখ্যা সংক্রান্ত ডেটা নেই। যাইহোক, 6% উদাহরণগুলির জন্য যেগুলিতে জনসংখ্যাগত বৈশিষ্ট্য রয়েছে, আমরা এখনও পৃথক ভবিষ্যদ্বাণীগুলির জোড়া তুলনা করতে পারি (একজন সংখ্যাগরিষ্ঠ প্রার্থী বনাম সংখ্যালঘু প্রার্থী) এবং দেখতে পারি যে মডেল দ্বারা তাদের ন্যায়সঙ্গত আচরণ করা হয়েছে কিনা।

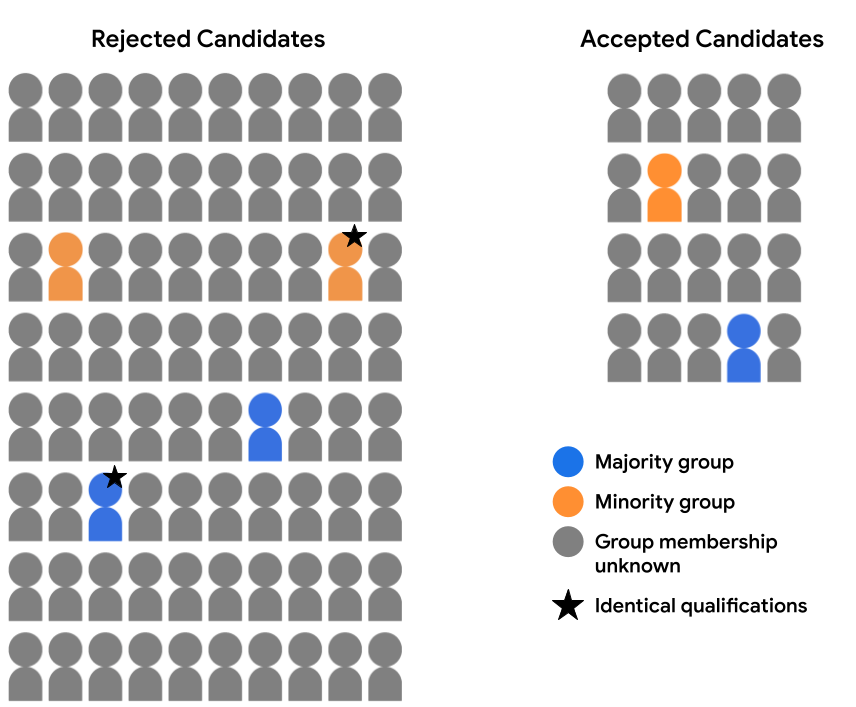
উদাহরণ স্বরূপ, ধরা যাক যে আমরা দুই প্রার্থীর জন্য উপলব্ধ বৈশিষ্ট্য ডেটা পুঙ্খানুপুঙ্খভাবে পর্যালোচনা করেছি (একজন সংখ্যাগরিষ্ঠ গোষ্ঠীতে এবং একজন সংখ্যালঘু গোষ্ঠীতে, নীচের ছবিতে একটি তারকা দিয়ে টীকা করা হয়েছে), এবং নির্ধারণ করেছি যে তারা অভিন্নভাবে যোগ্য সব ক্ষেত্রে ভর্তি। যদি মডেলটি এই উভয় প্রার্থীর জন্য একই ভবিষ্যদ্বাণী করে (অর্থাৎ, উভয় প্রার্থীকে প্রত্যাখ্যান করে বা উভয় প্রার্থীকে গ্রহণ করে), তবে এটি এই উদাহরণগুলির জন্য কাউন্টারফ্যাকচুয়াল ন্যায্যতাকে সন্তুষ্ট করতে বলা হয়। কাউন্টারফ্যাকচুয়াল ন্যায্যতা শর্ত দেয় যে দুটি উদাহরণ যা সমস্ত ক্ষেত্রে অভিন্ন, একটি প্রদত্ত সংবেদনশীল বৈশিষ্ট্য (এখানে, জনসংখ্যাগত গোষ্ঠীর সদস্যতা) ব্যতীত একই মডেলের ভবিষ্যদ্বাণী করা উচিত৷

পূর্ববর্তী চিত্রের মতো একই প্রার্থীর পুল, এই সংস্করণ ছাড়া, একটি নীল ছাত্র আইকন (সংখ্যাগরিষ্ঠ গোষ্ঠীর অন্তর্গত) এবং একটি কমলা ছাত্র আইকন (সংখ্যালঘু গোষ্ঠীর অন্তর্গত) প্রত্যাখ্যান করা গোষ্ঠীতে একটি তারা দিয়ে টীকা করা হয়েছে, যা নির্দেশ করে যে এইগুলি দুই প্রার্থী অভিন্ন (জনসংখ্যাগত গোষ্ঠী বাদে)।
চিত্র 6. একটি তারকা দিয়ে টীকা করা দুটি অভিন্ন উদাহরণ (শুধুমাত্র জনসংখ্যাগত গোষ্ঠীর সদস্যতায় পরিবর্তিত) জন্য কাউন্টারফ্যাকচুয়াল ন্যায্যতা সন্তুষ্ট, কারণ মডেল উভয়ের জন্য একই সিদ্ধান্ত নেয় (প্রত্যাখ্যাত)।

সুবিধা এবং অসুবিধা

পূর্বে উল্লিখিত হিসাবে, কাউন্টারফ্যাকচুয়াল ন্যায্যতার একটি মূল সুবিধা হল যে এটি অনেক ক্ষেত্রে ন্যায্যতার জন্য ভবিষ্যদ্বাণী মূল্যায়ন করতে ব্যবহার করা যেতে পারে যেখানে অন্যান্য মেট্রিক্স ব্যবহার করা সম্ভব হবে না। যদি একটি ডেটাসেটে বিবেচনাধীন প্রাসঙ্গিক গোষ্ঠী বৈশিষ্ট্যগুলির জন্য বৈশিষ্ট্যের মানগুলির সম্পূর্ণ সেট না থাকে, তাহলে জনসংখ্যার সমতা বা সুযোগের সমতা ব্যবহার করে ন্যায্যতা মূল্যায়ন করা সম্ভব হবে না। যাইহোক, যদি এই গোষ্ঠী বৈশিষ্ট্যগুলি উদাহরণগুলির একটি উপসেটের জন্য উপলব্ধ থাকে, এবং বিভিন্ন গোষ্ঠীতে সমতুল্য উদাহরণগুলির তুলনীয় জোড়া সনাক্ত করা সম্ভব হয়, তাহলে অনুশীলনকারীরা ভবিষ্যদ্বাণীতে সম্ভাব্য পক্ষপাতের জন্য মডেলটি তদন্ত করতে একটি মেট্রিক হিসাবে কাউন্টারফ্যাকচুয়াল ন্যায্যতা ব্যবহার করতে পারেন।

অতিরিক্তভাবে, যেহেতু জনসংখ্যাগত সমতা এবং সুযোগের সমতার মতো মেট্রিকগুলি সমষ্টিগতভাবে গোষ্ঠীগুলিকে মূল্যায়ন করে, তারা পক্ষপাতমূলক সমস্যাগুলিকে মুখোশ করতে পারে যা পৃথক ভবিষ্যদ্বাণীগুলির স্তরে মডেলকে প্রভাবিত করে, যা প্রতিফলিত ন্যায্যতা ব্যবহার করে মূল্যায়নের মাধ্যমে প্রকাশ করা যেতে পারে। উদাহরণ স্বরূপ, ধরুন আমাদের ভর্তির মডেল সংখ্যাগরিষ্ঠ গোষ্ঠী এবং সংখ্যালঘু গোষ্ঠীর যোগ্য প্রার্থীদেরকে একই অনুপাতে গ্রহণ করে, কিন্তু সবচেয়ে যোগ্য সংখ্যালঘু প্রার্থীকে প্রত্যাখ্যান করা হয় যেখানে সবচেয়ে যোগ্য সংখ্যাগরিষ্ঠ প্রার্থীকে গৃহীত হয় যার সঠিক একই শংসাপত্র রয়েছে। একটি কাউন্টারফ্যাকচুয়াল ন্যায্যতা বিশ্লেষণ এই ধরণের অসঙ্গতিগুলি সনাক্ত করতে সাহায্য করতে পারে যাতে সেগুলি সমাধান করা যায়।

উল্টোদিকে, কাউন্টারফ্যাকচুয়াল ন্যায্যতার মূল নেতিবাচক দিক হল যে এটি মডেল ভবিষ্যদ্বাণীতে পক্ষপাতের একটি সামগ্রিক দৃষ্টিভঙ্গি প্রদান করে না। উদাহরণগুলির জোড়ায় মুষ্টিমেয় বৈষম্য সনাক্ত করা এবং প্রতিকার করা পদ্ধতিগত পক্ষপাতের সমস্যাগুলি মোকাবেলা করার জন্য যথেষ্ট নাও হতে পারে যা উদাহরণগুলির সম্পূর্ণ উপগোষ্ঠীকে প্রভাবিত করে।

যে ক্ষেত্রে এটি সম্ভব, অনুশীলনকারীরা একটি সমষ্টিগত ন্যায্যতা বিশ্লেষণ (জনসংখ্যাগত সমতা বা সুযোগের সমতার মতো একটি মেট্রিক ব্যবহার করে) পাশাপাশি প্রতিকারের প্রয়োজনে সম্ভাব্য পক্ষপাতমূলক সমস্যাগুলির বিস্তৃত পরিসরের অন্তর্দৃষ্টি অর্জনের জন্য একটি কাউন্টারফ্যাকচুয়াল ন্যায্যতা বিশ্লেষণ উভয়ই বিবেচনা করতে পারেন৷

অনুশীলন: আপনার বোঝার পরীক্ষা করুন

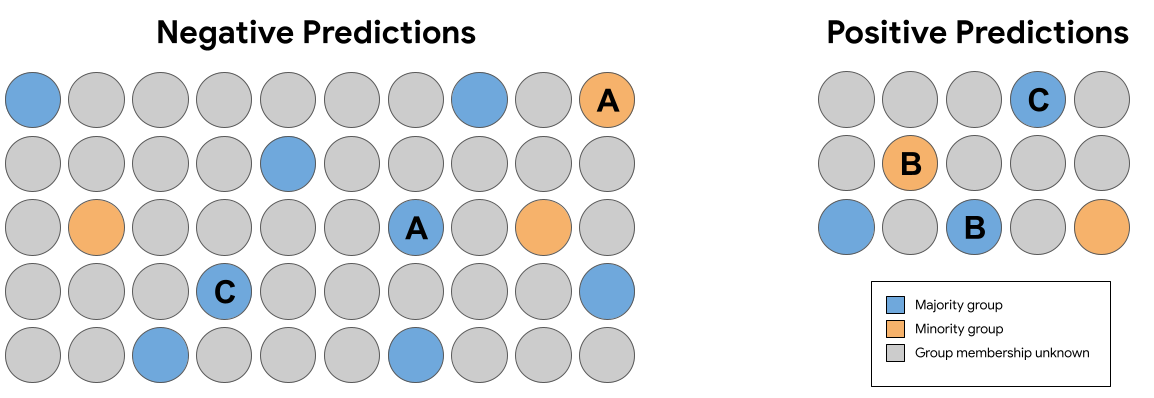
ব্যায়াম চিত্র। বৃত্তের দুটি গ্রুপ: নেতিবাচক ভবিষ্যদ্বাণী এবং ইতিবাচক ভবিষ্যদ্বাণী। নেতিবাচক ভবিষ্যদ্বাণী 50টি বৃত্ত নিয়ে গঠিত: 39টি ধূসর বৃত্ত, 8টি নীল বৃত্ত এবং 3টি কমলা বৃত্ত৷ একটি নীল বৃত্ত 'A' লেবেলযুক্ত, একটি কমলা বৃত্তে 'A' লেবেলযুক্ত, এবং একটি নীল বৃত্তকে 'C' লেবেল করা হয়েছে। ইতিবাচক ভবিষ্যদ্বাণী 15টি চেনাশোনা নিয়ে গঠিত: 10টি ধূসর বৃত্ত, 3টি নীল বৃত্ত এবং 2টি কমলা বৃত্ত৷ একটি নীল বৃত্ত 'B' লেবেলযুক্ত, একটি কমলা বৃত্তকে 'B' লেবেলযুক্ত, এবং একটি নীল বৃত্তকে 'C' লেবেল করা হয়েছে। ডায়াগ্রামের নীচের একটি কিংবদন্তি বলছে যে নীল চেনাশোনাগুলি সংখ্যাগরিষ্ঠ গোষ্ঠীতে একটি উদাহরণ উপস্থাপন করে, কমলা বৃত্তগুলি সংখ্যালঘু গোষ্ঠীতে একটি উদাহরণ উপস্থাপন করে এবং ধূসর বৃত্তগুলি এমন উদাহরণগুলিকে উপস্থাপন করে যাদের গ্রুপ সদস্যতা অজানা।
চিত্র 7. উদাহরণগুলির একটি ব্যাচের জন্য নেতিবাচক এবং ইতিবাচক ভবিষ্যদ্বাণী, A, B, এবং C হিসাবে লেবেলযুক্ত তিন জোড়া উদাহরণ সহ।

উপরের চিত্র 7-এর ভবিষ্যদ্বাণীগুলির সেটে, নিম্নলিখিতগুলির মধ্যে কোন জোড়া অভিন্ন (গ্রুপের সদস্যপদ ব্যতীত) উদাহরণগুলি ভবিষ্যদ্বাণী পেয়েছে যা কাউন্টারফ্যাকচুয়াল ন্যায্যতা লঙ্ঘন করে?

পেয়ার এ
পেয়ার A-এর ভবিষ্যদ্বাণীগুলি বাস্তবসম্মত ন্যায্যতাকে সন্তুষ্ট করে, কারণ সংখ্যাগরিষ্ঠ গোষ্ঠীর উদাহরণ (নীল) এবং সংখ্যালঘু গোষ্ঠীর উদাহরণ (কমলা) উভয়ই একই ভবিষ্যদ্বাণী (নেতিবাচক) পেয়েছে৷
জোড়া বি
পেয়ার B-এর ভবিষ্যদ্বাণীগুলি বাস্তবসম্মত ন্যায্যতাকে সন্তুষ্ট করে, কারণ সংখ্যাগরিষ্ঠ গোষ্ঠীর উদাহরণ (নীল) এবং সংখ্যালঘু গোষ্ঠীর উদাহরণ (কমলা) উভয়ই একই ভবিষ্যদ্বাণী (ইতিবাচক) পেয়েছে৷
পেয়ার সি
পেয়ার সি এর ভবিষ্যদ্বাণী দুটি উদাহরণের জন্য যে উভয়ই সংখ্যাগরিষ্ঠ গোষ্ঠীর (নীল) অন্তর্গত। মডেলটি এই অভিন্ন উদাহরণগুলির জন্য বিভিন্ন ভবিষ্যদ্বাণী তৈরি করেছে তা থেকে বোঝা যায় যে মডেলটির সাথে আরও বিস্তৃত কর্মক্ষমতা সমস্যা থাকতে পারে যা তদন্ত করা উচিত। যাইহোক, এই ফলাফলটি কাউন্টারফ্যাকচুয়াল ন্যায্যতা লঙ্ঘন করে না, যার শর্তগুলি শুধুমাত্র সেই ক্ষেত্রে প্রযোজ্য যেখানে দুটি অভিন্ন উদাহরণ প্রতিটি ভিন্ন গোষ্ঠী থেকে আঁকা হয়।
এই জোড়াগুলির কোনটিই কাউন্টারফ্যাকচুয়াল ন্যায্যতা লঙ্ঘন করে না
A এবং B জোড়ার জন্য ভবিষ্যদ্বাণীগুলি বাস্তবসম্মত ন্যায্যতাকে সন্তুষ্ট করে কারণ উভয় ক্ষেত্রেই, সংখ্যাগরিষ্ঠ গোষ্ঠীর উদাহরণ এবং সংখ্যালঘু গোষ্ঠীর উদাহরণ একই ভবিষ্যদ্বাণী পায়৷ পেয়ার সি-এর উদাহরণ উভয়ই একই গ্রুপের (সংখ্যাগরিষ্ঠ গোষ্ঠী) অন্তর্গত, তাই এই ক্ষেত্রে কাউন্টারফ্যাকচুয়াল ন্যায্যতা প্রযোজ্য নয়।

সারাংশ

জনসংখ্যার সমতা , সুযোগের সমতা , এবং প্রতিকূল ন্যায্যতা প্রতিটি মডেলের ভবিষ্যদ্বাণীর জন্য ন্যায্যতার বিভিন্ন গাণিতিক সংজ্ঞা প্রদান করে। এবং সেগুলি ন্যায্যতা পরিমাপ করার তিনটি সম্ভাব্য উপায়। ন্যায্যতার কিছু সংজ্ঞা এমনকি পারস্পরিকভাবে বেমানান , যার অর্থ একটি প্রদত্ত মডেলের ভবিষ্যদ্বাণীগুলির জন্য একই সাথে তাদের সন্তুষ্ট করা অসম্ভব।

তাহলে আপনি কিভাবে আপনার মডেলের জন্য "সঠিক" ন্যায্যতা মেট্রিক চয়ন করবেন? আপনি যে প্রেক্ষাপটে এটি ব্যবহার করা হচ্ছে এবং আপনি যে অত্যধিক লক্ষ্যগুলি অর্জন করতে চান তা বিবেচনা করতে হবে। উদাহরণস্বরূপ, লক্ষ্য কি সমান প্রতিনিধিত্ব অর্জন করা (এই ক্ষেত্রে, জনসংখ্যাগত সমতা সর্বোত্তম মেট্রিক হতে পারে) বা এটি কি সমান সুযোগ অর্জন করা (এখানে, সুযোগের সমতা সেরা মেট্রিক হতে পারে)?

এমএল ফেয়ারনেস সম্পর্কে আরও জানতে এবং এই বিষয়গুলি আরও গভীরভাবে অন্বেষণ করতে, সলোন বারোকাস, মরিটজ হার্ডট এবং অরবিন্দ নারায়ণনের ফেয়ারনেস এবং মেশিন লার্নিং: সীমাবদ্ধতা এবং সুযোগগুলি দেখুন।

পূর্ববর্তী
সুযোগের সমতা (10 মিনিট)
পরবর্তী
প্রোগ্রামিং ব্যায়াম (40 মিনিট)