Jusqu'à présent, nos discussions sur les métriques d'équité ont supposé que notre formation et les exemples de test contiennent des données démographiques complètes sous-groupes en cours d’évaluation. Mais ce n'est souvent pas le cas.
Supposons que notre ensemble de données sur les admissions ne contient pas de données démographiques complètes. L'appartenance à un groupe démographique n'est enregistrée que pour un faible pourcentage d'exemples, comme les élèves qui ont choisi d'identifier eux-mêmes le groupe auquel appartenaient. Dans ce cas, la répartition de notre pool de candidats en candidats et les élèves rejetés se présente comme suit:
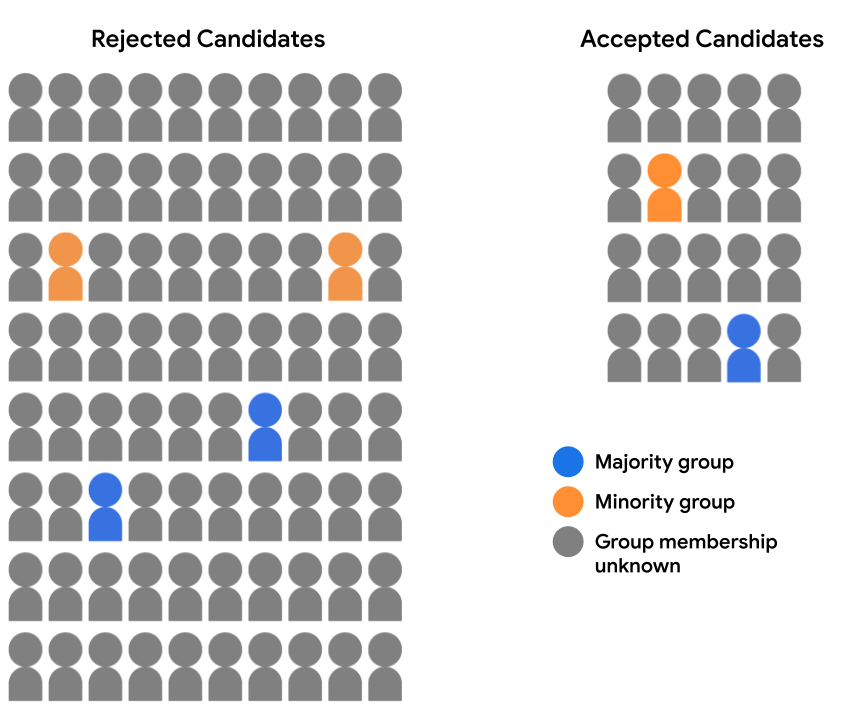
Il n'est pas possible d'évaluer les prédictions du modèle pour les données démographiques la parité ou l'égalité des chances, car nous ne disposons pas de données démographiques pour 94% de nos exemples. Toutefois, pour les 6% d'exemples contenant les caractéristiques démographiques, il est toujours possible de comparer des paires de prédictions individuelles (un candidat à la majorité ou d'une minorité) et voyez s'il a été de façon équitable par le modèle.
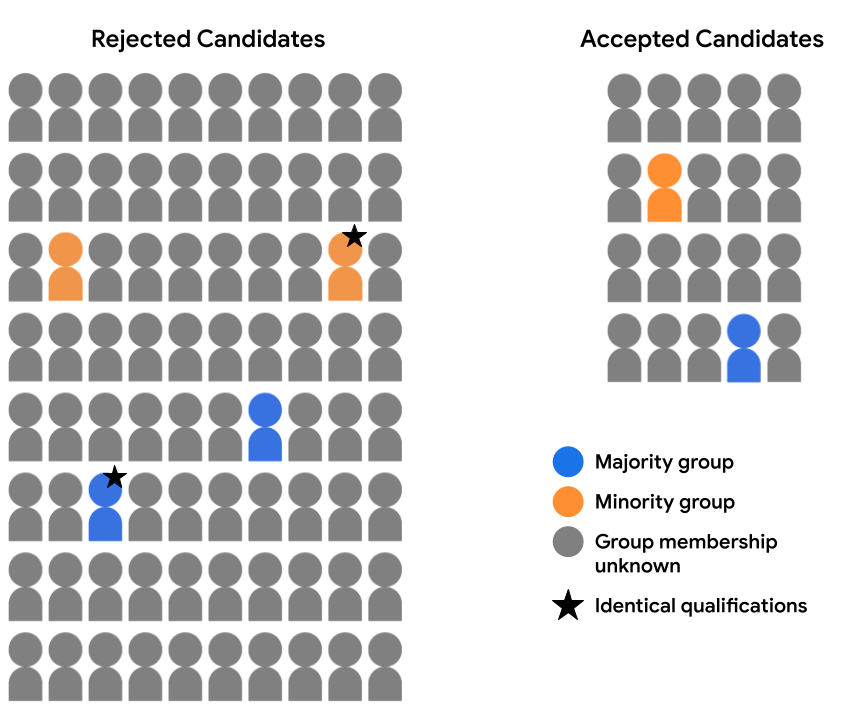
Imaginons, par exemple, que nous ayons examiné en détail les données de caractéristiques disponible pour deux candidats (un dans le groupe majoritaire et l'autre dans la minorité) , annotée avec une étoile dans l'image ci-dessous) et a déterminé qu'elle sont éligibles à tous égards. Si le modèle fait la même prédiction pour ces deux candidats (c'est-à-dire que l'un ou l'autre rejette les deux ou accepte les deux), elle satisfait aux constatations contradictoires équitable pour ces exemples. L’impartialité contrefactuelle stipule que deux Exemples identiques à tous égards, à l'exception d'un attribut sensible donné (dans le cas présent, l'appartenance à un groupe démographique), doit donner le même modèle la prédiction.
Avantages et inconvénients
Comme mentionné précédemment, l'un des principaux avantages de l'impartialité contrefactuelle est qu'elle peut servir à évaluer l'équité des prédictions dans de nombreux cas où l'utilisation d’autres métriques ne serait pas faisable. Si un jeu de données ne contient pas un ensemble complet des valeurs de caractéristiques pour les attributs de groupe pertinents en cours de considération, d'évaluer l'impartialité à l'aide de la parité démographique ou de l'égalité des opportunité. Toutefois, si ces attributs de groupe sont disponibles pour un sous-ensemble d'exemples, et il est possible d'identifier des paires comparables exemples appartenant à différents groupes, les professionnels peuvent avoir recours à l'impartialité contrefactuelle comme métrique pour détecter d'éventuels biais dans les prédictions du modèle.
De plus, comme des métriques telles que la parité démographique et l'égalité des les opportunités évaluent les groupes de façon globale, ils peuvent masquer des problèmes de biais qui affectent le modèle au niveau des prédictions individuelles, lesquelles peuvent être mises en évidence à l'aide d'une équité contrefactuelle. Par exemple, supposons que nos admissions accepte les candidats qualifiés du groupe majoritaire et de la minorité dans la même proportion, mais le candidat de la minorité la plus qualifiée est rejetés, alors que le candidat le plus qualifié ayant obtenu la même identifiants de connexion est accepté. Une analyse d’impartialité contrefactuelle peut aider à identifier ce genre d'écarts afin qu'ils puissent être résolus.
D'un autre côté, l'inconvénient clé de l'impartialité contrefactuelle est qu'elle ne offrent une vision globale des biais dans les prédictions du modèle. L’identification et corriger quelques inégalités par paires d'exemples n'est peut-être pas suffisant. pour résoudre les problèmes de biais systémiques qui affectent des sous-groupes entiers d’exemples.
Lorsque cela est possible, ils peuvent envisager d'effectuer à la fois un agrégat une analyse de l'impartialité (à l'aide d'une métrique telle que la parité démographique ou l'égalité des opportunité) et d'une analyse d'équité contrefactuelle pour obtenir la un ensemble d'insights sur les problèmes de biais potentiels à corriger.
Exercice: tester vos connaissances
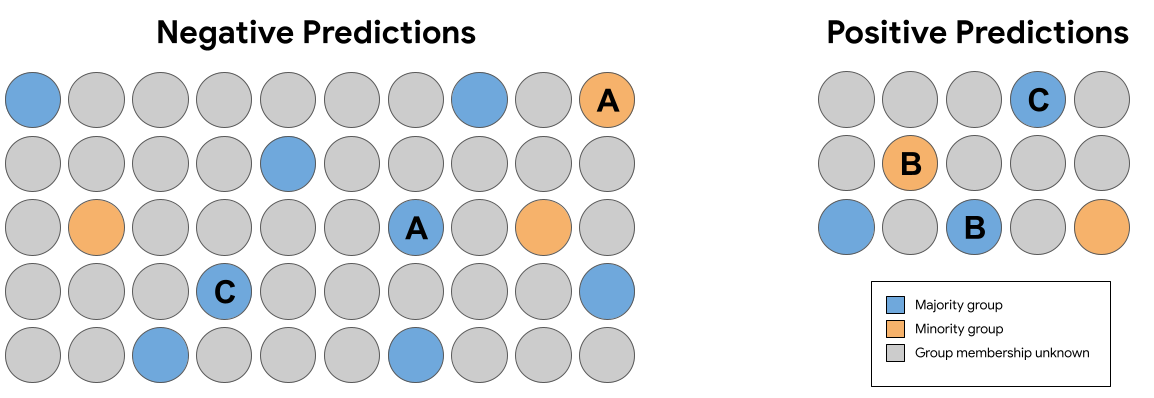
Parmi les prédictions de la figure 7 ci-dessus, laquelle paires suivantes d'identiques identiques (à l'exception des membres d'un groupe) exemples reçus de prédictions qui enfreignent l'équité contrefactuelle ?
Résumé
Parité démographique l'égalité des chances, et l'impartialité contrefactuelle fournissent chacune des définitions mathématiques différentes de l'équité pour les prédictions du modèle. Et ce ne sont que trois possibles moyens de quantifier l’impartialité. Certaines définitions de l'impartialité sont même mutuellement incompatibles, ce qui signifie qu'il peut être impossible de les satisfaire en même temps les prédictions d'un modèle donné.
Alors, comment choisir le "bon" d'équité de votre modèle ? Vous devez tenez compte du contexte dans lequel elles sont utilisées et des objectifs globaux que vous souhaitez accomplir. Par exemple, l'objectif est-il d'obtenir une représentation égale (dans ce cas, la parité démographique peut être la métrique optimale) ou à atteindre l'égalité des chances (ici, l'égalité des chances peut être métrique) ?
Pour en savoir plus sur l'équité en matière de ML et explorer ces questions plus en détail, consultez Fairness and Machine Learning: Limitations and Opportunities de Solon Barocas, Moritz Hardt et Arvind Narayanan.
