До сих пор в наших обсуждениях показателей справедливости предполагалось, что наши примеры обучения и тестирования содержат полные демографические данные для оцениваемых демографических подгрупп. Но часто это не так.
Предположим, наш набор данных о поступлении не содержит полных демографических данных. Вместо этого членство в демографической группе фиксируется лишь для небольшого процента примеров, например, для студентов, которые решили самостоятельно определить, к какой группе они принадлежат. В этом случае разбивка нашего пула кандидатов на принятых и отклоненных студентов теперь выглядит следующим образом:
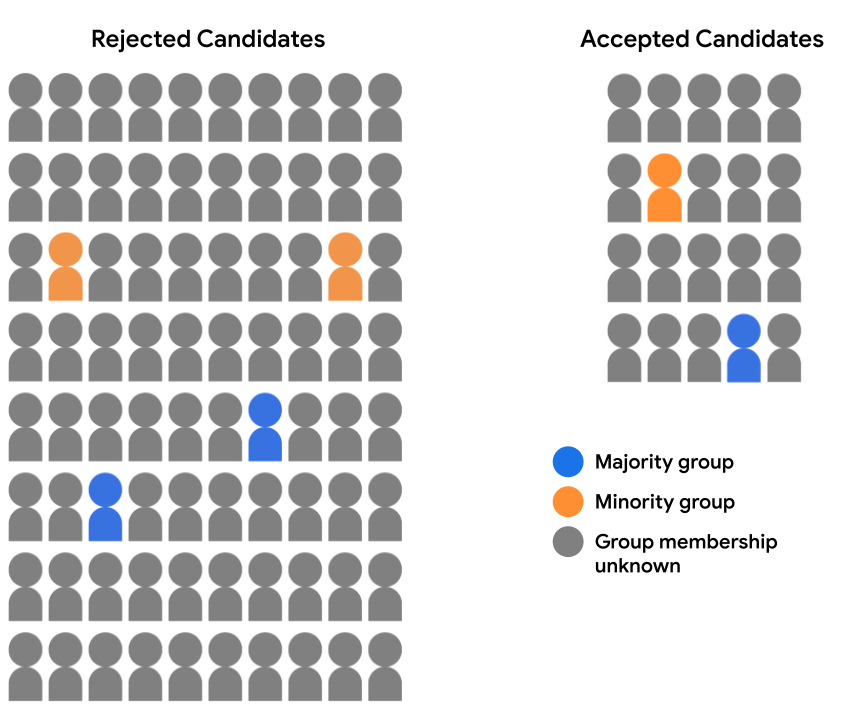
Здесь невозможно оценить прогнозы модели на предмет демографического паритета или равенства возможностей, поскольку у нас нет демографических данных для 94% наших примеров. Однако для 6% примеров, которые содержат демографические характеристики, мы все равно можем сравнить пары отдельных прогнозов (кандидат большинства и кандидат меньшинства) и посмотреть, справедливо ли они рассматриваются моделью.
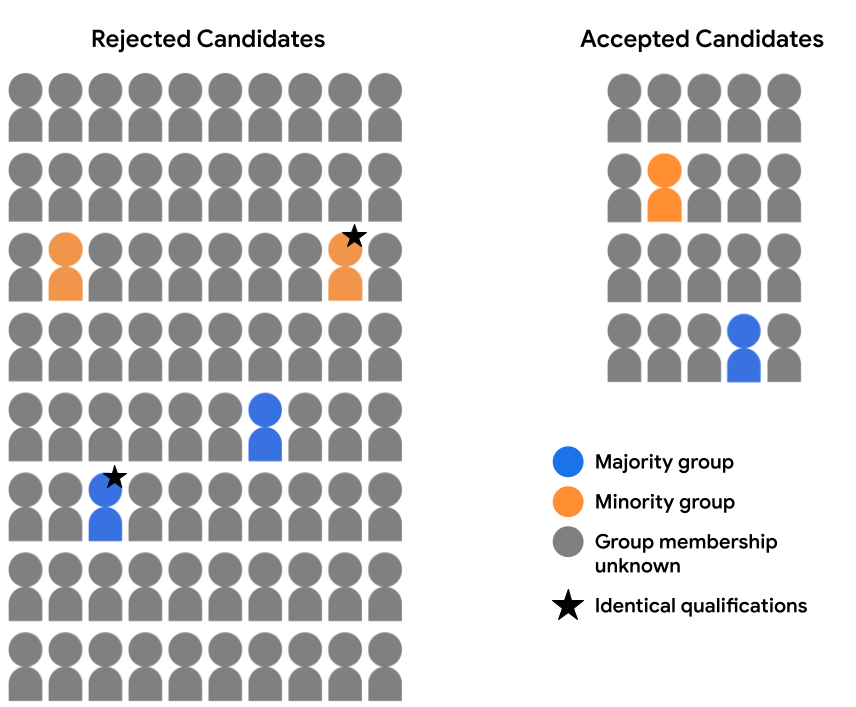
Например, предположим, что мы тщательно просмотрели данные о характеристиках, доступные для двух кандидатов (одного из группы большинства и одного из группы меньшинства, отмеченных звездочкой на изображении ниже), и определили, что они одинаково подходят для прием во всех отношениях. Если модель делает одинаковый прогноз для обоих этих кандидатов (т. е. либо отвергает обоих кандидатов, либо принимает обоих кандидатов), говорят, что она удовлетворяет контрфактической справедливости для этих примеров. Контрфактическая справедливость предполагает, что два примера, идентичные во всех отношениях, за исключением данного чувствительного атрибута (в данном случае членства в демографической группе), должны привести к одному и тому же предсказанию модели.
Преимущества и недостатки
Как упоминалось ранее, одним из ключевых преимуществ контрфактической справедливости является то, что ее можно использовать для оценки справедливости прогнозов во многих случаях, когда использование других показателей было бы невозможно. Если набор данных не содержит полного набора значений признаков для соответствующих рассматриваемых групповых атрибутов, невозможно будет оценить справедливость, используя демографический паритет или равенство возможностей. Однако если эти групповые атрибуты доступны для подмножества примеров и можно идентифицировать сопоставимые пары эквивалентных примеров в разных группах, практики могут использовать контрфактическую справедливость в качестве показателя для проверки модели на предмет потенциальных ошибок в прогнозах.
Кроме того, поскольку такие показатели, как демографический паритет и равенство возможностей, оценивают группы в совокупности, они могут маскировать проблемы предвзятости, которые влияют на модель на уровне индивидуальных прогнозов, которые могут быть выявлены путем оценки с использованием контрфактической справедливости. Например, предположим, что наша модель приема принимает квалифицированных кандидатов из группы большинства и группы меньшинства в одинаковой пропорции, но наиболее квалифицированный кандидат из меньшинства отклоняется, тогда как принимается наиболее квалифицированный кандидат из большинства, имеющий точно такие же полномочия. Контрфактический анализ справедливости может помочь выявить такого рода несоответствия и устранить их.
С другой стороны, ключевым недостатком контрфактической справедливости является то, что она не дает целостного представления о предвзятости в предсказаниях модели. Выявление и устранение небольшого количества неравенств в парах примеров может быть недостаточным для решения проблем системной предвзятости, которые затрагивают целые подгруппы примеров.
В тех случаях, когда это возможно, специалисты-практики могут рассмотреть возможность проведения как совокупного анализа справедливости (с использованием таких показателей, как демографический паритет или равенство возможностей), так и контрфактического анализа справедливости, чтобы получить максимально широкий спектр понимания потенциальных проблем предвзятости, нуждающихся в исправлении.
Упражнение: Проверьте свое понимание.
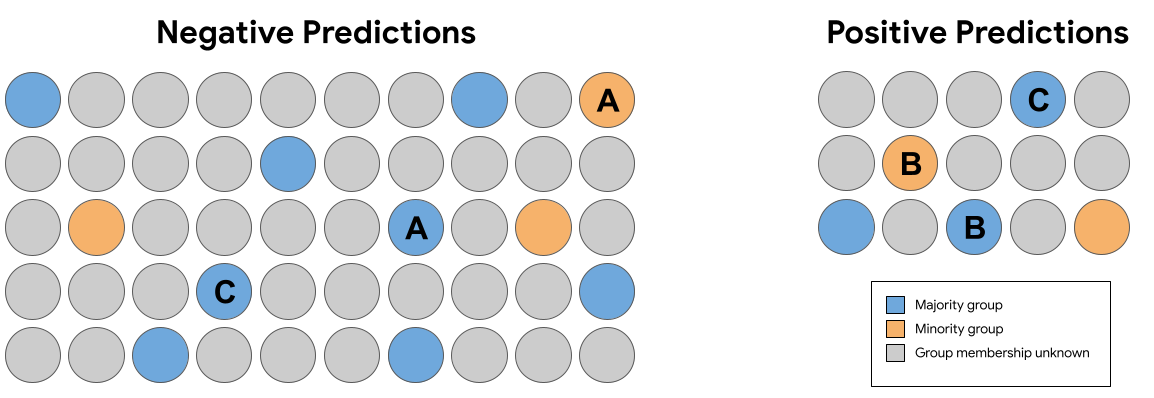
В наборе прогнозов на рисунке 7 выше, какая из следующих пар идентичных (исключая членство в группе) примеров получила прогнозы, которые нарушают контрфактическую справедливость?
Краткое содержание
Демографический паритет , равенство возможностей и контрфактическая справедливость дают разные математические определения справедливости для прогнозов модели. И это всего лишь три возможных способа количественной оценки справедливости. Некоторые определения справедливости даже несовместимы друг с другом , а это означает, что может оказаться невозможным удовлетворить их одновременно для прогнозов данной модели.
Так как же выбрать «правильный» показатель справедливости для вашей модели? Вам необходимо учитывать контекст, в котором он используется, и основные цели, которых вы хотите достичь. Например, является ли целью достижение равного представительства (в данном случае оптимальным показателем может быть демографический паритет) или достижение равных возможностей (в данном случае равенство возможностей может быть лучшим показателем)?
Чтобы узнать больше о справедливости ML и более подробно изучить эти проблемы, см. статью «Справедливость и машинное обучение: ограничения и возможности» Солона Барокаса, Морица Хардта и Арвинда Нараянана.
