Досі, розглядаючи метрику справедливості, ми припускали, що навчальні й тестові приклади містять вичерпні демографічні дані для підгруп населення, які оцінюються. Але часто це не так.
Припустімо, що набір даних моделі моделі відбору кандидатів не містить усіх демографічних даних. Натомість приналежність до групи населення реєструється лише для невеликого відсотка прикладів (зокрема студентів, які вирішили самостійно зазначити, до якої групи вони належать). У цьому разі розподіл пулу кандидатів на прийнятих і відхилених студентів виглядає так:
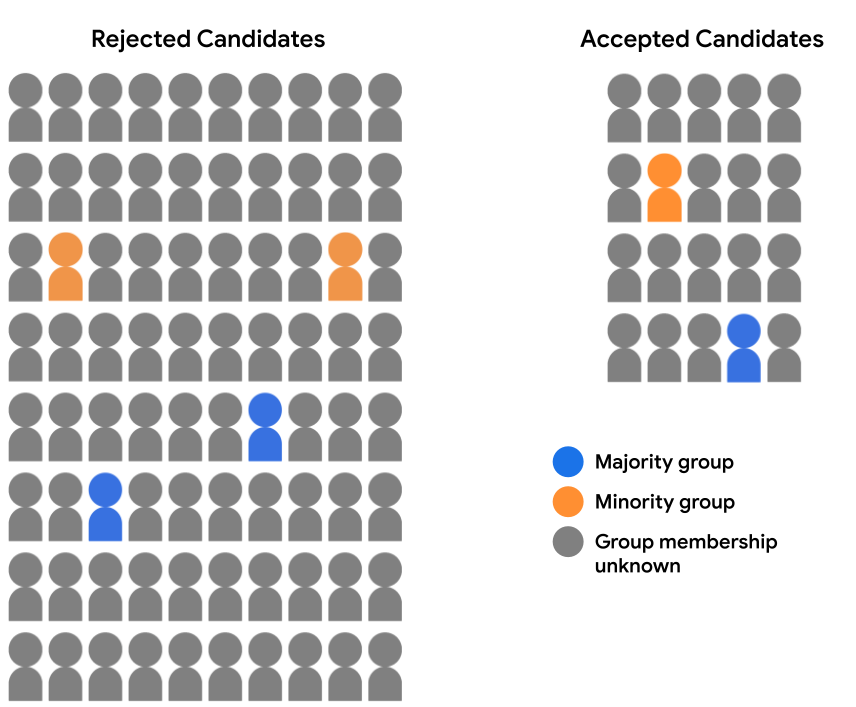
У такому разі неможливо оцінити, наскільки прогнози моделі відповідають принципам демографічної рівності чи рівності можливостей, оскільки немає демографічних даних для 94% прикладів. Однак для 6% прикладів, які містять демографічні ознаки, можна порівняти пари окремих прогнозів (кандидат від більшості проти кандидата від меншості) і побачити, чи модель розглядала їх справедливо.
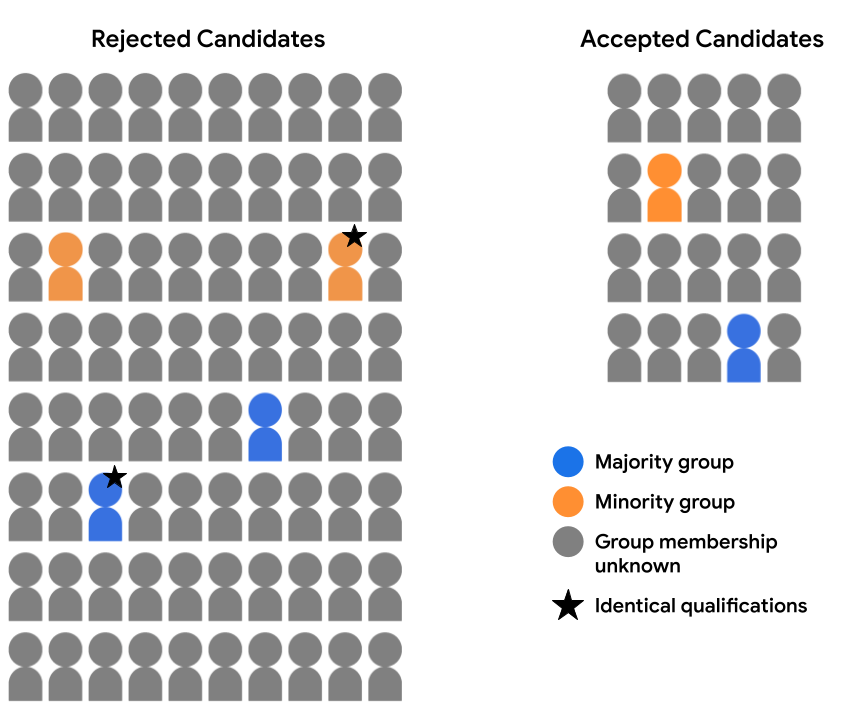
Припустімо, що ми ретельно переглянули дані ознак, доступні для двох кандидатів (одного з групи більшості й одного з групи меншості, які позначено зірочкою на зображенні нижче), і виявили, що вони мають однакове право бути прийнятими, як не поглянути. Якщо модель робить однаковий прогноз для обох цих кандидатів (тобто або відхиляє, або приймає їх обох), вважається, що її результати для цих прикладів відповідають вимозі контрфактичної справедливості. Контрфактична справедливість передбачає, що для двох прикладів, які є ідентичними, як не поглянути, за винятком певного чутливого атрибута (у нашому прикладі це приналежність до певної групи населення), модель має дати однаковий прогноз.
Переваги й недоліки
Як згадувалося раніше, однією з ключових переваг контрфактичної справедливості є те, що її часто можна використовувати для оцінювання прогнозів на справедливість тоді, коли застосувати інші метрики неможливо. Якщо в наборі даних немає всіх значень ознак для відповідних групових атрибутів, що розглядаються, неможливо буде оцінити справедливість, використовуючи метрики демографічної рівності або рівності можливостей. Однак якщо ці групові атрибути доступні для підмножини прикладів і можна ідентифікувати порівнювані пари еквівалентних прикладів у різних групах, спеціалісти можуть використовувати контрфактичну справедливість як метрику для перевірки моделі на наявність потенційних упередженостей у прогнозах.
Крім того, оскільки такі метрики, як демографічна рівність і рівність можливостей, оцінюють групи в сукупності, вони можуть маскувати проблеми упередженості, що впливають на модель на рівні окремих прогнозів. Їх можна виявити, використовуючи для оцінювання контрфактичну справедливість. Припустімо, що наша модель відбору кандидатів приймає кваліфікованих кандидатів із груп більшості й меншості в однаковій пропорції. Проте вона відхилила найкваліфікованішого кандидата з групи меншості, а найкращого студента з групи більшості, ідентичного за кваліфікацією, прийняла. Аналіз контрфактичної справедливості може допомогти виявити подібні розбіжності, щоб їх можна було усунути.
З іншого боку, основним недоліком контрфактичної справедливості є те, що вона не дає настільки цілісного уявлення про упередженість у прогнозах моделі, як інші метрики. Іноді недостатньо виявити й усунути кілька нерівностей у парах прикладів, щоб вирішити системні проблеми упередженості, які впливають на цілі підгрупи прикладів.
Якщо можливо провести як сукупний (використовуючи таку метрику, як демографічна рівність або рівність можливостей), так і контрфактичний аналіз справедливості, спеціалістам-практикам слід розглянути цей варіант, адже так вони отримають якнайбільше даних про потенційні проблеми упередженості, що потребують виправлення.
Вправа. Перевірте свої знання
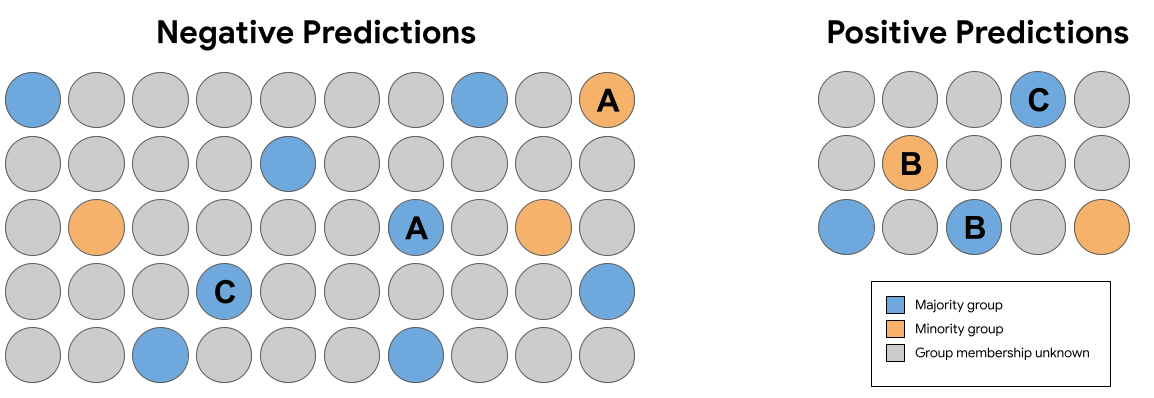
Розгляньте ряд прогнозів, показаних на рисунку 7 вище. Прогнози якої з пар ідентичних (за винятком приналежності до групи) прикладів, наведених нижче, порушують принцип контрфактичної справедливості?
Підсумок
Демографічна рівність, рівність можливостей і контрфактична справедливість мають різні математичні визначення справедливості для прогнозів моделі. І це лише три способи кількісної оцінки справедливості. Деякі визначення справедливості є навіть взаємно несумісними, тобто прогнози однієї моделі не можуть відповідати їм одночасно.
Тож як вибрати "правильну" метрику справедливості для моделі? Потрібно враховувати контекст, у якому вона використовується, і головні цілі, яких ви хочете досягти. Наприклад, якщо потрібно досягти однакової кількості представників різних груп населення, оптимальною метрикою може бути демографічна рівність; а якщо ви хочете надавати однакові можливості, найвідповіднішою метрикою, імовірно, є рівність можливостей.
Щоб дізнатися більше про справедливість у машинному навчанні й глибше дослідити ці питання, прочитайте книгу Fairness and Machine Learning: Limitations and Opportunities (Справедливість і машинне навчання: обмеження й можливості), яку написали Солон Барокас, Моріц Хардт і Арвінд Нараянан.