ในส่วนก่อนหน้านี้ เราประเมินรูปแบบการรับนักศึกษาเพื่อความเป็นธรรมโดยใช้ ความเท่าเทียมกันของข้อมูลประชากร โดยการเปรียบเทียบอัตราการยอมรับโดยรวมสำหรับ กลุ่มผู้เข้าชม
หรือเราอาจเปรียบเทียบอัตราการยอมรับสำหรับเฉพาะผู้ที่เข้าเกณฑ์ ผู้สมัครรับเลือกตั้งในกลุ่มใหญ่และชนกลุ่มน้อย หากอัตราการยอมรับ สำหรับนักเรียนที่มีคุณสมบัติตามเกณฑ์ของทั้ง 2 กลุ่มเท่ากัน โมเดลจะแสดง ความเท่าเทียมของโอกาส: นักเรียนที่มีป้ายกำกับที่ต้องการ ("มีคุณสมบัติเข้าสอบ") จะได้รับ โอกาสที่จะได้รับเลือก ไม่ว่าจะอยู่ในกลุ่มประชากรใดก็ตาม เป็น
มาดูกลุ่มผู้สมัครของเราจากส่วนก่อนหน้ากันอีกครั้ง
| กลุ่มคะแนนเสียงข้างมาก | ชนกลุ่มน้อย | |
|---|---|---|
| ผ่านเกณฑ์ | 35 | 15 |
| ไม่เข้าเกณฑ์ | 45 | 5 |
สมมติว่ารูปแบบการรับนักศึกษายอมรับผู้สมัคร 14 คนจากกลุ่มส่วนใหญ่ และผู้สมัคร 6 คนจากชนกลุ่มน้อย การตัดสินใจของโมเดลเป็นไปตาม ความเท่าเทียมกันของโอกาส เนื่องจากอัตราการยอมรับเสียงข้างมากของทั้ง 2 ฝ่าย และผู้สมัครที่เป็นชนกลุ่มน้อย ที่เข้าเกณฑ์คือ 40%
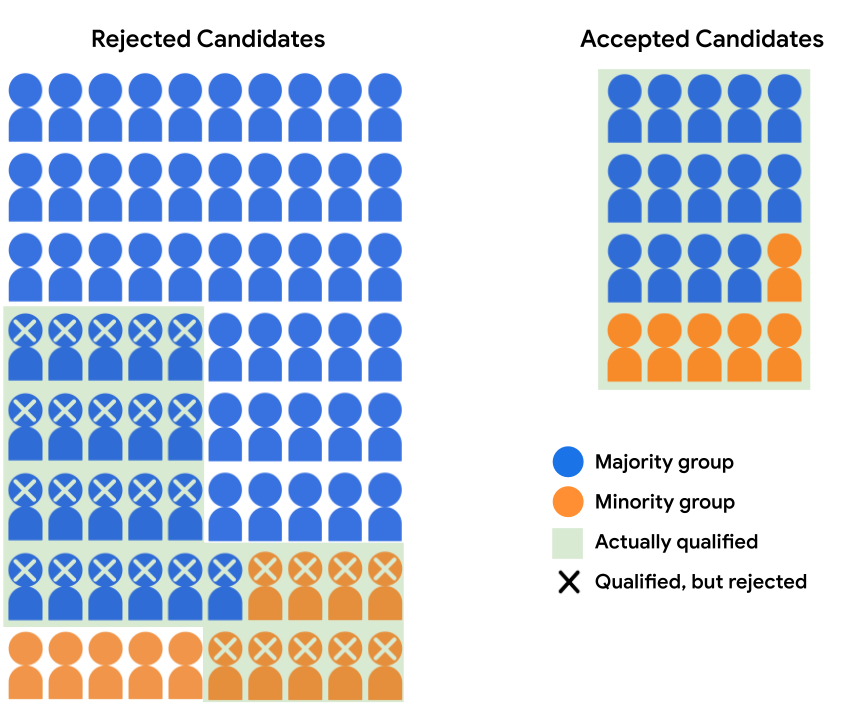
ตารางต่อไปนี้แสดงจำนวนตัวเลขที่สนับสนุนรายการที่ถูกปฏิเสธและได้รับการยอมรับ ผู้สมัครในรูปที่ 4
| กลุ่มคะแนนเสียงข้างมาก | ชนกลุ่มน้อย | |||
|---|---|---|---|---|
| ยอมรับ | ถูกปฏิเสธ | ยอมรับ | ถูกปฏิเสธ | |
| ผ่านเกณฑ์ | 14 | 21 | 6 | 9 |
| ไม่เข้าเกณฑ์ | 0 | 45 | 0 | 5 |
ข้อดีและข้อเสีย
ประโยชน์หลักของความเท่าเทียมของโอกาสคือ ทำให้โมเดล อัตราส่วนของการคาดการณ์เชิงบวกต่อเชิงลบจะแตกต่างกันไปในกลุ่มข้อมูลประชากร หากโมเดลประสบความสำเร็จในการคาดการณ์ป้ายกำกับที่ต้องการอย่างเท่าเทียมกัน ("เข้าเกณฑ์ในการเข้าร่วม") สำหรับทั้ง 2 กลุ่ม
การคาดการณ์โมเดลในรูปที่ 4 ไม่เป็นไปตามความเท่าเทียมกันของข้อมูลประชากร ในฐานะนักเรียนในกลุ่มส่วนใหญ่ จะมีโอกาสได้รับการยอมรับ 17.5% และ นักเรียนในชนกลุ่มน้อยจะมีโอกาส 30% ที่จะได้รับการยอมรับ อย่างไรก็ตาม นักเรียนที่มีคุณสมบัติผ่านเกณฑ์มีโอกาส 40% ที่จะได้รับการยอมรับ กลุ่มที่ตนอยู่ ซึ่งน่าจะได้ผลลัพธ์ที่ยุติธรรมกว่า กรณีการใช้งานรุ่นที่เจาะจง
ข้อด้อยประการหนึ่งของความเท่าเทียมของโอกาสคือ ออกแบบมาเพื่อให้ใช้งาน กรณีที่มีป้ายกำกับที่ต้องการแบบชัดเจน ถ้าค่าใช้จ่ายนั้นสำคัญเท่ากัน โมเดลคาดการณ์ทั้งคลาสเชิงบวก ("เข้าเกณฑ์สำหรับการเข้าศึกษา") และประเภทเชิงลบ ("ไม่มีสิทธิ์เข้าร่วม") สำหรับกลุ่มข้อมูลประชากรทั้งหมด คุณอาจต้องใช้เมตริกแทน โอกาสอย่างเท่าเทียมกัน ซึ่งบังคับใช้ อัตราความสำเร็จของป้ายกำกับทั้ง 2 ป้ายเท่ากัน
ข้อเสียอีกประการของโอกาสความเท่าเทียมคือการประเมินความเป็นธรรม
ด้วยการเปรียบเทียบอัตราข้อผิดพลาดโดยรวมสำหรับกลุ่มข้อมูลประชากร ซึ่งอาจ
อาจเป็นไปได้เสมอไป เช่น ถ้าชุดข้อมูลของโมเดลการเข้าศึกษา
ไม่มีฟีเจอร์ของ demographic_group จึงไม่สามารถ
แจกแจงอัตราการตอบรับของผู้สมัครเสียงข้างมากและชนกลุ่มน้อยที่เข้าเกณฑ์
และเปรียบเทียบโอกาสเหล่านี้เพื่อดูว่าเราพึงพอใจกับความเท่าเทียมของโอกาสหรือไม่
ในส่วนถัดไป เราจะมาดูเมตริกด้านความยุติธรรมอีกอย่างหนึ่ง ซึ่งก็คือ ความเป็นธรรม ซึ่งสามารถนำมาใช้ได้ในกรณีที่ข้อมูลประชากรไม่ สำหรับตัวอย่างทั้งหมด
แบบฝึกหัด: ตรวจสอบความเข้าใจ
การคาดการณ์ของโมเดลสามารถตอบสนองความต้องการทั้งทางข้อมูลประชากรได้ ความเท่าเทียมและความเท่าเทียมของโอกาส
ตัวอย่างเช่น สมมติว่ามีตัวแยกประเภทแบบไบนารี (ซึ่งมีป้ายกำกับที่ต้องการ เป็นคลาสเชิงบวก) ได้รับการประเมินจากตัวอย่าง 100 รายการ โดยมีผลลัพธ์ ที่แสดงในเมทริกซ์ความสับสนต่อไปนี้ แยกตาม กลุ่มประชากร (กลุ่มใหญ่และชนกลุ่มน้อย):
| กลุ่มคะแนนเสียงข้างมาก | ชนกลุ่มน้อย | |||
|---|---|---|---|---|
| คาดการณ์ไว้ในแง่บวก | ค่าลบที่คาดการณ์ | คาดการณ์ไว้ในแง่บวก | ค่าลบที่คาดการณ์ | |
| ผลบวกจริง | 6 | 12 | 3 | 6 |
| ผลลบจริง | 10 | 36 | 6 | 21 |
|
\(\text{Positive Rate} = \frac{6+10}{6+10+12+36} = \frac{16}{64} = \text{25%}\) \(\text{True Positive Rate} = \frac{6}{6+12} = \frac{6}{18} = \text{33%}\) |
\(\text{Positive Rate} = \frac{3+6}{3+6+6+21} = \frac{9}{36} = \text{25%}\) \(\text{True Positive Rate} = \frac{3}{3+6} = \frac{3}{9} = \text{33%}\) |
|||
ทั้งกลุ่มส่วนใหญ่และชนกลุ่มน้อยมีอัตราการคาดการณ์เป็นบวก 25% พึงพอใจกับความเท่าเทียมกันของข้อมูลประชากร และอัตราเชิงบวกที่แท้จริง (เปอร์เซ็นต์ของตัวอย่างที่มีป้ายกำกับที่ต้องการซึ่ง ได้รับการจัดประเภทอย่างถูกต้อง) จาก 33% เป็นที่น่าพอใจเกี่ยวกับความเท่าเทียมของโอกาส
