Overfitting

Per overfitting si intende la creazione di un modello che corrisponde (memorizza) al set di addestramento con una tale precisione da non riuscire a fare previsioni corrette sui nuovi dati. Un modello overfit è analogo a un'invenzione che funziona bene in laboratorio, ma è inutile nel mondo reale.

Nella Figura 11, immagina che ogni forma geometrica rappresenti la posizione di un albero in una foresta quadrata. I rombi blu indicano la posizione degli alberi sani, mentre i cerchi arancioni indicano la posizione degli alberi malati.

Figura 11. Questa figura contiene circa 60 punti, la metà dei quali rappresenta alberi sani e l'altra metà alberi malati. Gli alberi sani si trovano principalmente nel quadrante nord-est, anche se alcuni si trovano nei quadranti nord-ovest. Gli alberi malati si trovano principalmente nel quadrante sud-est, ma alcuni si estendono anche in altri quadranti.
Figura 11. Set di addestramento: posizioni di alberi sani e malati in una foresta quadrata.

 

Disegna mentalmente qualsiasi forma: linee, curve, ovali e così via per separare gli alberi sani da quelli malati. Poi, espandi la riga successiva per esaminare una possibile separazione.

Le forme complesse mostrate nella Figura 12 hanno classificato correttamente tutti gli alberi tranne due. Se consideriamo le forme come un modello, questo è un modello fantastico.

O no? Un modello davvero eccellente classifica correttamente gli esempi nuovi. La Figura 13 mostra cosa succede quando lo stesso modello fa previsioni su nuovi esempi del set di test:

Figura 13. Un nuovo lotto di alberi sani e malati sovrapposto al modello mostrato nella Figura 12. Il modello classifica erroneamente molti degli alberi.
Figura 13. Set di test: un modello complesso per distinguere gli alberi sani da quelli malati.

 

Pertanto, il modello complesso mostrato nella Figura 12 ha ottenuto ottimi risultati sul set di addestramento, ma risultati piuttosto scadenti sul set di test. Questo è un caso classico di overfitting del modello ai dati del set di addestramento.

Adattamento, overfitting e underfitting

Un modello deve fare buone previsioni su dati nuovi. In altre parole, vuoi creare un modello che "si adatti" ai nuovi dati.

Come hai visto, un modello overfit fa previsioni eccellenti sul set di addestramento, ma previsioni scarse sui nuovi dati. Un modello sottoadattato non fa nemmeno buone previsioni sui dati di addestramento. Se un modello overfit è come un prodotto che funziona bene in laboratorio, ma male nel mondo reale, un modello underfit è come un prodotto che non funziona bene nemmeno in laboratorio.

Figura 14. Grafico cartesiano. L'asse x è etichettato come "qualità delle previsioni sul set di addestramento". L'asse Y è etichettato come "qualità delle previsioni su dati reali". Una curva inizia nell'origine e aumenta gradualmente, ma poi scende altrettanto rapidamente. La parte in basso a sinistra della curva (bassa qualità delle previsioni sui dati reali e bassa qualità delle previsioni sul set di addestramento) è etichettata come "modelli sottostimati". La parte in basso a destra della curva (bassa qualità delle previsioni su dati reali, ma alta qualità delle previsioni sul set di addestramento) è etichettata come "modelli overfit". Il picco della curva (alta qualità delle previsioni sui dati reali e media qualità delle previsioni sul set di addestramento) è etichettato come "modelli adatti".
Figura 14. Modelli sottostimati, adattati e con overfitting.

 

La generalizzazione è l'opposto dell'overfitting. In altre parole, un modello che generalizza bene fa buone previsioni su nuovi dati. Il tuo obiettivo è creare un modello che si generalizzi bene ai nuovi dati.

Rilevamento dell'overfitting

Le seguenti curve ti aiutano a rilevare il sovraadattamento:

  • curve di perdita
  • curve di generalizzazione

Una curva di perdita traccia la perdita di un modello rispetto al numero di iterazioni di addestramento. Un grafico che mostra due o più curve di perdita è chiamato curva di generalizzazione. La seguente curva di generalizzazione mostra due curve di perdita:

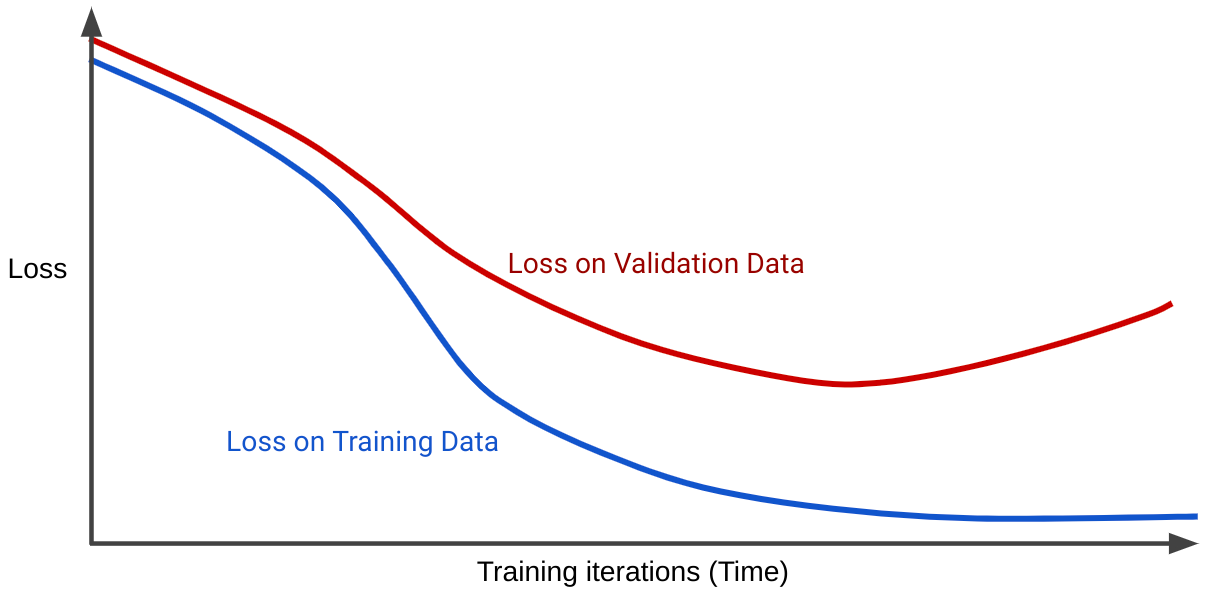
Figura 15. La funzione di perdita per l'insieme di addestramento diminuisce gradualmente. Anche la funzione di perdita per il set di convalida diminuisce, ma poi inizia ad aumentare dopo un certo numero di iterazioni.
Figura 15. Una curva di generalizzazione che implica fortemente l'overfitting.

 

Nota che le due curve di perdita si comportano in modo simile all'inizio e poi divergono. In altre parole, dopo un certo numero di iterazioni, la perdita diminuisce o rimane invariata (converge) per il set di addestramento, ma aumenta per il set di convalida. Ciò suggerisce un overfitting.

Al contrario, una curva di generalizzazione per un modello ben adattato mostra due curve di perdita con forme simili.

Quali sono le cause dell'overfitting?

In termini molto generali, l'overfitting è causato da uno o entrambi i seguenti problemi:

  • Il set di addestramento non rappresenta adeguatamente i dati reali (o il set di convalida o il set di test).
  • Il modello è troppo complesso.

Condizioni di generalizzazione

Un modello viene addestrato su un set di addestramento, ma il vero test del suo valore è la sua capacità di fare previsioni su nuovi esempi, in particolare su dati reali. Durante lo sviluppo di un modello, il set di test funge da sostituto dei dati reali. L'addestramento di un modello che generalizza bene implica le seguenti condizioni del set di dati:

  • Gli esempi devono essere distribuiti in modo indipendente e identico, che è un modo elegante per dire che i tuoi esempi non possono influenzarsi a vicenda.
  • Il set di dati è stazionario, il che significa che non cambia in modo significativo nel tempo.
  • Le partizioni del set di dati hanno la stessa distribuzione. In altre parole, gli esempi nel set di addestramento sono statisticamente simili agli esempi nel set di convalida, nel set di test e nei dati reali.

Esplora le condizioni precedenti con i seguenti esercizi.

Esercizi: verifica la comprensione

Considera le seguenti partizioni del set di dati.
Una barra orizzontale divisa in tre parti: il 70% della barra è il set di addestramento, il 15% il set di convalida e il 15% il set di test
Che cosa devi fare per assicurarti che gli esempi nel set di addestramento abbiano una distribuzione statistica simile a quella degli esempi nel set di convalida e nel set di test?
Mescola ampiamente gli esempi nel set di dati prima di suddividerli.
Sì. Un buon rimescolamento degli esempi rende le partizioni molto più simili dal punto di vista statistico.
Ordina gli esempi dal più antico al più recente.
Se gli esempi nel set di dati non sono stazionari, l'ordinamento rende le partizioni meno simili.
Non fare niente. Dati esempi sufficienti, la legge delle medie garantisce naturalmente che le distribuzioni saranno statisticamente simili.
Purtroppo non è così. Gli esempi in alcune sezioni del set di dati possono essere diversi da quelli in altre sezioni.
Un servizio di streaming sta sviluppando un modello per prevedere la popolarità di potenziali nuovi programmi televisivi per i prossimi tre anni. Il servizio di streaming prevede di addestrare il modello su un set di dati contenente centinaia di milioni di esempi, che coprono i dieci anni precedenti. Questo modello presenterà un problema?
È probabile. I gusti degli spettatori cambiano in modi che non possono essere previsti dal comportamento passato.
Sì. I gusti degli spettatori non sono statici. Sono in continua evoluzione.
Assolutamente no. Il set di dati è abbastanza grande per fare buone previsioni.
Purtroppo, i gusti degli spettatori non sono stazionari.
Probabilmente no. I gusti degli spettatori cambiano in modo ciclico e prevedibile. Dieci anni di dati consentiranno al modello di fare buone previsioni sulle tendenze future.
Anche se alcuni aspetti dell'intrattenimento sono in qualche modo ciclici, un modello addestrato sulla base della cronologia dell'intrattenimento passata avrà quasi certamente difficoltà a fare previsioni per i prossimi anni.
Un modello mira a prevedere il tempo impiegato dalle persone per percorrere un chilometro in base ai dati meteorologici (temperatura, punto di rugiada e precipitazioni) raccolti nell'arco di un anno in una città il cui clima varia notevolmente in base alla stagione. Puoi creare e testare un modello da questo set di dati, anche se le letture meteo cambiano notevolmente in base alla stagione?
Sì
Sì, è possibile creare e testare un modello da questo set di dati. Devi solo assicurarti che i dati siano partizionati in modo uniforme, in modo che i dati di tutte e quattro le stagioni siano distribuiti equamente nelle diverse partizioni.
No
Supponendo che questo set di dati contenga esempi sufficienti di temperatura, punto di rugiada e precipitazioni, puoi creare e testare un modello da questo set di dati. Devi solo assicurarti che i dati siano suddivisi in modo uniforme, in modo che i dati di tutte e quattro le stagioni siano distribuiti equamente nelle diverse partizioni.

Esercizio della sfida

Stai creando un modello che preveda la data ideale per l'acquisto di un biglietto ferroviario per un determinato percorso. Ad esempio, il modello potrebbe consigliare agli utenti di acquistare il biglietto l'8 luglio per un treno che parte il 23 luglio. La compagnia ferroviaria aggiorna i prezzi ogni ora, in base a una serie di fattori, ma principalmente al numero corrente di posti disponibili. Ossia:

  • Se sono disponibili molti posti, i prezzi dei biglietti sono in genere bassi.
  • Se sono disponibili pochissimi posti, i prezzi dei biglietti sono in genere elevati.
Il tuo modello presenta una perdita bassa sul set di convalida e sul set di test, ma a volte fa previsioni terribili sui dati reali. Perché?
Fai clic qui per vedere la risposta
Indietro
Generalizzazione (5 min)
Avanti
Complessità modello (10 min)