过拟合是指创建的模型与训练集过于匹配(记忆),以致于模型无法根据新数据做出正确的预测。过拟合模型类似于在实验室中表现出色但在现实世界中毫无用处的发明。
在图 11 中,假设每个几何图形都代表方形森林中的一棵树的位置。蓝色菱形标记健康树木的位置,而橙色圆圈标记病树的位置。

在脑海中画出任何形状(线条、曲线、椭圆形...任何形状)来将健康的树与生病的树分开。然后,展开下一行,检查其中一个可能的分离。
图 12 中显示的复杂形状成功对除两棵树以外的所有树进行了分类。如果我们将这些形状视为模型,那么这是一个非常棒的模型。
或者说有可能?真正出色的模型能够成功对新示例进行分类。图 13 显示了当同一模型对测试集中的新示例进行预测时会发生的情况:

因此,图 12 中显示的复杂模型在训练集中的表现非常出色,但在测试集中的表现非常糟糕。这是模型对训练集数据过拟合的典型示例。
拟合、过拟合和欠拟合
模型必须能对新数据做出良好的预测。也就是说,您要创建一个能“拟合”新数据的模型。
如您所见,过拟合模型在训练集上可以做出出色的预测,但在新数据上做出的预测却不准确。欠拟合模型甚至无法对训练数据做出准确的预测。如果过拟合模型就像在实验室中表现出色但在现实世界中表现不佳的产品,那么欠拟合模型就像在实验室中表现不佳的产品。

泛化与过拟合相反。也就是说,泛化能力强的模型可以对新数据做出良好的预测。您的目标是创建一个能够很好地泛化到新数据的模型。
检测过拟合
以下曲线可帮助您检测过拟合:
- 损失曲线
- 泛化曲线
损失曲线会将模型的损失与训练迭代次数绘制在图表中。显示两个或更多损失曲线的图表称为泛化曲线。以下泛化曲线显示了两个损失曲线:
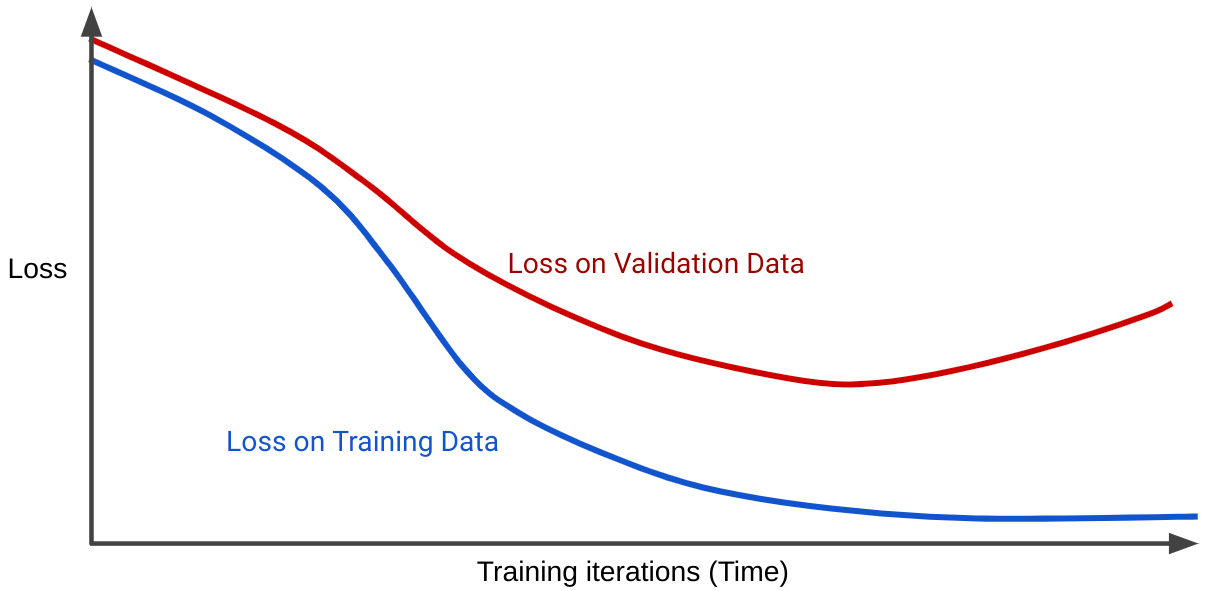
请注意,这两个损失曲线最初的行为类似,然后开始分歧。也就是说,经过一定次数的迭代后,训练集的损失会下降或保持稳定(收敛),但验证集的损失会增加。这表明模型过拟合。
相比之下,适合度较高的模型的泛化曲线会显示两个形状相似的损失曲线。
什么会导致过拟合?
一般来说,过拟合是由以下一种或两种问题导致的:
- 训练集不能充分代表真实数据(或验证集或测试集)。
- 模型过于复杂。
泛化条件
模型在训练集中进行训练,但真正检验模型价值的标准是它对新示例(尤其是真实数据)的预测效果如何。在开发模型时,测试集可用作真实数据的替代项。训练能够很好地泛化到新数据的模型,需要满足以下数据集条件:
- 示例必须独立且等概率分布,这是一种巧妙的方式,表示您的示例不能相互影响。
- 数据集是平稳的,这意味着数据集不会随时间的推移而发生显著变化。
- 数据集分区具有相同的分布。也就是说,训练集中的示例在统计上与验证集、测试集和真实数据中的示例相似。
通过以下练习探索上述条件。
练习:检查您的理解情况

挑战练习
您要创建一个模型,用于预测乘客购买特定路线火车票的理想日期。例如,该模型可能会建议用户在 7 月 8 日购买 7 月 23 日出发的火车票。火车公司每小时更新一次价格,更新依据多种因素,但主要取决于当前的空余座位数。具体来说:
- 如果有大量空座,票价通常较低。
- 如果空座非常少,票价通常较高。
答案:真实模型在处理反馈环方面存在问题。
例如,假设模型建议用户在 7 月 8 日购买票券。 一些乘客根据模型的建议,于 7 月 8 日上午 8:30 购买了票券。9:00 时,火车公司上调了价格,因为此时有售的座位数量较少。使用模型建议的乘客更改了价格。到了晚上,票价可能会比早上高出很多。

