Surapprentissage

Le surapprentissage consiste à créer un modèle qui correspond (mémorise) si étroitement à l'ensemble d'entraînement qu'il ne parvient pas à effectuer des prédictions correctes avec de nouvelles données. Un modèle suradapté est semblable à une invention qui fonctionne bien en laboratoire, mais qui est sans valeur dans le monde réel.

Dans la figure 11, imaginez que chaque forme géométrique représente la position d'un arbre dans une forêt carrée. Les losanges bleus indiquent l'emplacement des arbres sains, tandis que les cercles orange indiquent l'emplacement des arbres malades.

Figure 11 : Cette illustration contient environ 60 points, dont la moitié représente des arbres sains et l'autre moitié des arbres malades. Les arbres sains se trouvent principalement dans le quadrant nord-est, bien que quelques arbres sains se glissent dans les quadrants nord-ouest. Les arbres malades se trouvent principalement dans le quadrant sud-est, mais certains se sont propagés dans d'autres quadrants.
Figure 11 : Ensemble d'entraînement: emplacements des arbres sains et malades dans une forêt carrée.

 

Dessinez mentalement des formes (lignes, courbes, ovales, etc.) pour séparer les arbres sains des arbres malades. Développez ensuite la ligne suivante pour examiner une séparation possible.

Les formes complexes illustrées à la figure 12 ont réussi à classer tous les arbres, à l'exception de deux. Si nous considérons les formes comme un modèle, il s'agit d'un modèle fantastique.

ou presque… Un modèle vraiment excellent parvient à classer les nouveaux exemples. La figure 13 montre ce qui se passe lorsque ce même modèle effectue des prédictions sur de nouveaux exemples de l'ensemble de test:

Figure 13 Nouveau lot d'arbres sains et malades superposés au modèle illustré à la figure 12. Le modèle catégorise mal de nombreux arbres.
Figure 13 : Ensemble de test : modèle complexe permettant de distinguer les arbres malades des arbres sains.

 

Ainsi, le modèle complexe illustré à la figure 12 a très bien fait avec l'ensemble d'entraînement, mais très mal avec l'ensemble de test. Il s'agit d'un cas classique de surapprentissage d'un modèle par rapport aux données de l'ensemble d'entraînement.

Ajustement, surapprentissage et sous-apprentissage

Un modèle doit fournir de bonnes prédictions sur de nouvelles données. Autrement dit, vous souhaitez créer un modèle qui "s'adapte" aux nouvelles données.

Comme vous l'avez vu, un modèle suradapté effectue d'excellentes prédictions sur l'ensemble d'entraînement, mais de mauvaises prédictions sur les nouvelles données. Un modèle sous-adapté ne fournit même pas de bonnes prédictions sur les données d'entraînement. Si un modèle suradapté est comme un produit qui fonctionne bien en laboratoire, mais mal dans le monde réel, un modèle sous-adapté est comme un produit qui ne fonctionne même pas bien en laboratoire.

Figure 14. Graphique cartésien. L'axe X est intitulé "Qualité des prédictions sur l'ensemble d'entraînement". L'axe Y est intitulé "Qualité des prédictions sur des données réelles". Une courbe commence à l'origine et augmente progressivement, mais diminue ensuite tout aussi rapidement. La partie inférieure gauche de la courbe (faible qualité des prédictions sur les données réelles et faible qualité des prédictions sur l'ensemble d'entraînement) est intitulée "Modèles sous-adaptés". La partie inférieure droite de la courbe (mauvaise qualité des prédictions sur les données réelles, mais bonne qualité des prédictions sur l'ensemble d'entraînement) est intitulée "Modèles sur-adaptés". Le pic de la courbe (qualité élevée des prédictions sur les données réelles et qualité moyenne des prédictions sur l'ensemble d'entraînement) est associé à "Modèles d'ajustement".
Figure 14 : Modèles sous-adaptés, adaptés et suradaptés

 

La généralisation est l'opposé du surapprentissage. Autrement dit, un modèle qui se prête bien à la généralisation effectue de bonnes prédictions sur les nouvelles données. Votre objectif est de créer un modèle correctement généralisable par rapport aux nouvelles données.

Détecter le surapprentissage

Les courbes suivantes vous aident à détecter un surapprentissage:

  • courbes de fonction de perte
  • courbes de généralisation

Une courbe de perte représente la perte d'un modèle en fonction du nombre d'itérations d'entraînement. Un graphique qui montre deux ou plusieurs courbes de perte est appelé courbe de généralisation. La courbe de généralisation suivante présente deux courbes de perte:

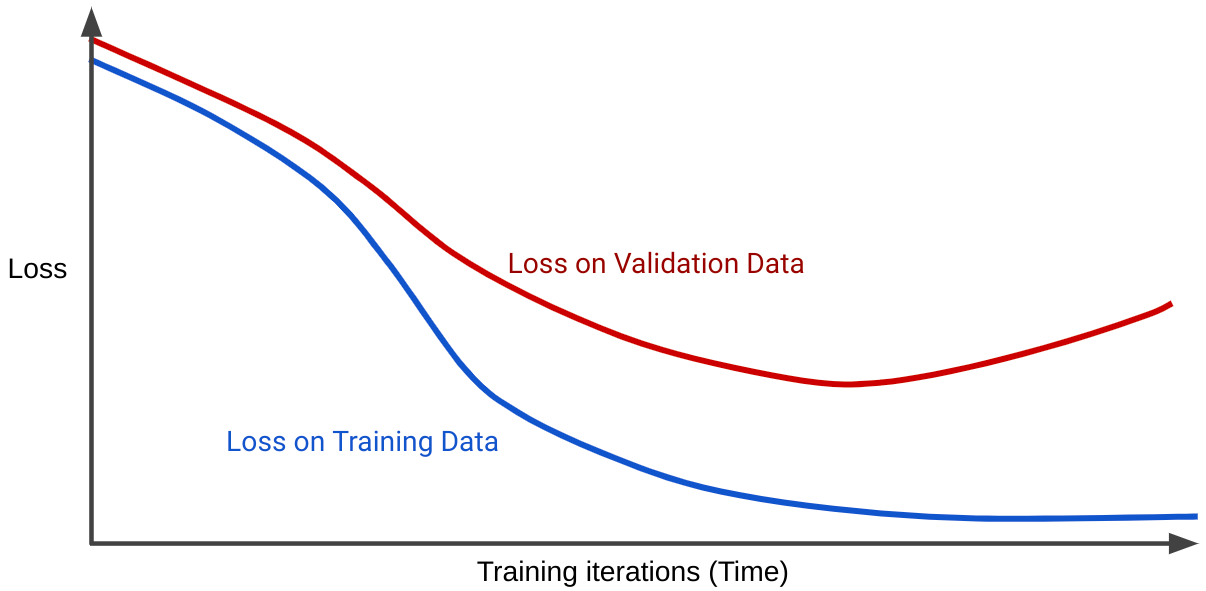
Figure 15. La fonction de perte de l'ensemble d'entraînement diminue progressivement. La fonction de perte de l'ensemble de validation diminue également, mais commence à augmenter après un certain nombre d'itérations.
Figure 15 : Courbe de généralisation qui implique fortement un surapprentissage.

 

Notez que les deux courbes de perte se comportent de manière similaire au début, puis divergent. Autrement dit, après un certain nombre d'itérations, la perte diminue ou reste stable (converge) pour l'ensemble d'entraînement, mais augmente pour l'ensemble de validation. Cela suggère un surapprentissage.

En revanche, une courbe de généralisation pour un modèle bien ajusté affiche deux courbes de perte de forme similaire.

Quelles sont les causes du surapprentissage ?

De manière très générale, le surajustement est dû à l'un ou aux deux problèmes suivants:

  • L'ensemble d'entraînement ne représente pas de manière adéquate les données réelles (ni l'ensemble de validation ni l'ensemble de test).
  • Le modèle est trop complexe.

Conditions de généralisation

Un modèle est entraîné sur un ensemble d'entraînement, mais le véritable test de la valeur d'un modèle est la qualité de ses prédictions sur de nouveaux exemples, en particulier sur des données réelles. Lors du développement d'un modèle, votre ensemble de test sert de proxy pour les données réelles. Pour entraîner un modèle qui se généralise bien, vous devez respecter les conditions suivantes pour l'ensemble de données:

  • Les exemples doivent être distribués indépendamment et de manière identique, ce qui revient à dire que vos exemples ne peuvent pas s'influencer les uns les autres.
  • L'ensemble de données est stationnaire, ce qui signifie qu'il ne change pas de manière significative au fil du temps.
  • Les partitions de l'ensemble de données ont la même distribution. Autrement dit, les exemples de l'ensemble d'entraînement sont statistiquement similaires aux exemples de l'ensemble de validation, de l'ensemble de test et des données réelles.

Découvrez les conditions précédentes à l'aide des exercices suivants.

Exercices: Testez vos connaissances

Prenons les partitions d'ensemble de données suivantes.
Barre horizontale divisée en trois parties: 70% de la barre représente l'ensemble d'entraînement, 15% l'ensemble de validation et 15 % l'ensemble de test.
Que devez-vous faire pour vous assurer que les exemples de l'ensemble d'entraînement ont une distribution statistique similaire à celle des exemples de l'ensemble de validation et de l'ensemble de test ?
Mélangez de manière approfondie les exemples de l'ensemble de données avant de les partitionner.
Oui. Un bon mélange des exemples rend les partitions beaucoup plus susceptibles d'être statistiquement similaires.
Triez les exemples de la plus ancienne à la plus récente.
Si les exemples de l'ensemble de données ne sont pas stationnaires, le tri rend les partitions moins similaires.
Ne rien faire. Avec suffisamment d'exemples, la loi des moyennes garantit naturellement que les distributions seront statistiquement similaires.
Malheureusement, ce n'est pas le cas. Les exemples de certaines sections du jeu de données peuvent différer de ceux d'autres sections.
Un service de streaming développe un modèle pour prédire la popularité de nouvelles émissions de télévision potentielles pour les trois prochains ans. Le service de streaming prévoit d'entraîner le modèle sur un ensemble de données contenant des centaines de millions d'exemples, couvrant les dix dernières années. Ce modèle rencontrera-t-il un problème ?
Probablement. Les goûts des spectateurs changent de manière imprévisible par rapport au comportement passé.
Oui. Les goûts des spectateurs ne sont pas statiques. Elles changent constamment.
Certainement pas. Le jeu de données est suffisamment volumineux pour effectuer de bonnes prédictions.
Malheureusement, les goûts des spectateurs ne sont pas stationnaires.
Probablement pas. Les goûts des spectateurs évoluent de manière cyclique prévisible. Dix ans de données permettront au modèle de faire de bonnes prédictions sur les tendances futures.
Bien que certains aspects du divertissement soient quelque peu cycliques, un modèle entraîné à partir de l'histoire du divertissement passé aura presque certainement du mal à faire des prédictions pour les prochaines années.
Un modèle vise à prédire le temps qu'il faut aux utilisateurs pour parcourir un kilomètre à pied en fonction des données météorologiques (température, point de rosée et précipitations) collectées sur une année dans une ville dont les conditions météorologiques varient considérablement selon les saisons. Pouvez-vous créer et tester un modèle à partir de cet ensemble de données, même si les relevés météorologiques changent considérablement en fonction de la saison ?
Oui
Oui, il est possible de créer et de tester un modèle à partir de cet ensemble de données. Vous devez simplement vous assurer que les données sont partitionnées de manière égale, de sorte que les données des quatre saisons soient réparties de manière égale dans les différentes partitions.
Non
En supposant que cet ensemble de données contient suffisamment d'exemples de température, de point de rosée et de précipitations, vous pouvez créer et tester un modèle à partir de cet ensemble de données. Vous devez simplement vous assurer que les données sont partitionnées de manière égale, afin que les données des quatre saisons soient réparties de manière égale dans les différentes partitions.

Exercice de défi

Vous créez un modèle qui prédit la date idéale pour que les passagers achètent un billet de train pour un trajet donné. Par exemple, le modèle peut recommander aux utilisateurs d'acheter leur billet le 8 juillet pour un train qui part le 23 juillet. La compagnie ferroviaire met à jour les prix toutes les heures, en fonction de divers facteurs, mais principalement du nombre de sièges disponibles. Par exemple :

  • Si de nombreuses places sont disponibles, les prix des billets sont généralement bas.
  • Si très peu de places sont disponibles, les prix des billets sont généralement élevés.
Votre modèle présente une faible perte sur l'ensemble de validation et l'ensemble de test, mais effectue parfois de mauvaises prédictions sur des données réelles. Pourquoi ?
Cliquez ici pour voir la réponse
Précédent
Généralisation (5 min)
Suivant
Complexité du modèle (10 min)