과적합이란 학습 세트와 너무 유사하여 새 데이터를 올바르게 예측하지 못하는 모델을 만드는 것을 의미합니다 (학습). 과적합 모델은 실험실에서는 잘 작동하지만 실제 환경에서는 쓸모가 없는 발명품과 비슷합니다.
그림 11에서 각 도형은 정사각형 숲에 있는 나무의 위치를 나타냅니다. 파란색 다이아몬드는 건강한 나무의 위치를, 주황색 원은 아픈 나무의 위치를 표시합니다.

선, 곡선, 타원 등 어떤 도형이든 상상하여 그려 건강한 나무와 아픈 나무를 구분합니다. 그런 다음 다음 줄을 펼쳐 가능한 분리를 하나씩 살펴봅니다.
그림 12에 표시된 복잡한 도형은 나무 중 두 개를 제외하고 모두 분류했습니다. 도형을 모델로 생각하면 멋진 모델입니다.
정말 불가능할까요? 정말 우수한 모델은 새로운 예시를 성공적으로 분류합니다. 그림 13은 동일한 모델이 테스트 세트의 새 예시를 예측할 때 어떤 일이 일어나는지 보여줍니다.

따라서 그림 12에 표시된 복잡한 모델은 학습 세트에서 매우 우수한 성능을 보였지만 테스트 세트에서는 매우 좋지 않은 성능을 보였습니다. 이는 모델이 학습 세트 데이터에 과적합하는 전형적인 사례입니다.
적합, 과적합, 과소적합
모델은 새 데이터를 잘 예측해야 합니다. 즉, 새 데이터에 '맞는' 모델을 만드는 것이 목표입니다.
보시다시피 과적합 모델은 학습 세트에서는 우수한 예측을 하지만 새 데이터에서는 예측이 좋지 않습니다. 적합도 부족 모델은 학습 데이터를 제대로 예측하지 못합니다. 과적합 모델은 실험실에서는 잘 작동하지만 실제 환경에서는 잘 작동하지 않는 제품과 같고, 언더피팅 모델은 실험실에서도 잘 작동하지 않는 제품과 같습니다.

일반화는 과적합의 반대입니다. 즉, 일반화 성능이 우수한 모델은 새 데이터를 잘 예측합니다. 새로운 데이터에 잘 일반화되는 모델을 만드는 것이 목표입니다.
과적합 감지
다음 곡선을 사용하면 과적합을 감지할 수 있습니다.
- 손실 곡선
- 일반화 곡선
손실 곡선은 모델의 손실을 학습 반복 횟수에 대해 표시합니다. 두 개 이상의 손실 곡선을 보여주는 그래프를 일반화 곡선이라고 합니다. 다음 일반화 곡선은 두 가지 손실 곡선을 보여줍니다.
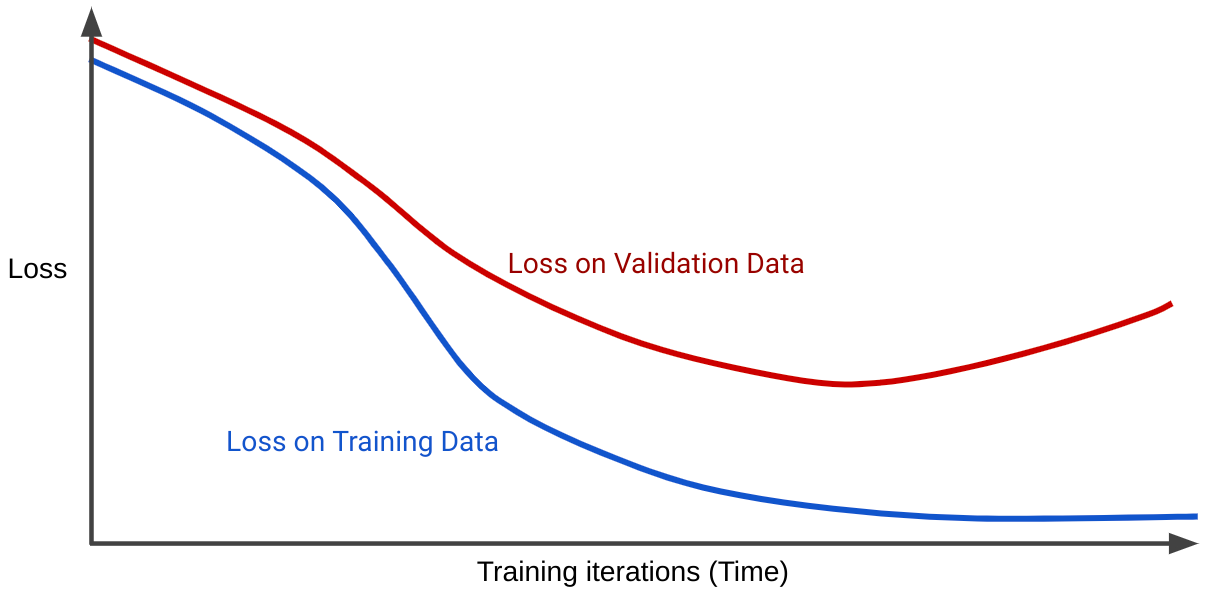
두 손실 곡선이 처음에는 비슷하게 동작하다가 나중에 갈라지는 것을 볼 수 있습니다. 즉, 일정 횟수의 반복 후 학습 세트의 손실은 감소하거나 일정하게 유지되지만 (수렴) 검증 세트의 손실은 증가합니다. 이는 과적합을 나타냅니다.
반대로 잘 맞는 모델의 일반화 곡선은 모양이 비슷한 두 개의 손실 곡선을 보여줍니다.
과적합의 원인은 무엇인가요?
대략적으로 오버피팅은 다음 문제 중 하나 또는 둘 다로 인해 발생합니다.
- 학습 세트가 실제 데이터 (또는 검증 세트 또는 테스트 세트)를 충분히 대표하지 않습니다.
- 모델이 너무 복잡합니다.
일반화 조건
모델은 학습 세트에서 학습하지만 모델의 가치를 실제로 테스트하려면 새 예시, 특히 실제 데이터에서 얼마나 잘 예측하는지 확인해야 합니다. 모델을 개발하는 동안 테스트 세트는 실제 데이터의 프록시 역할을 합니다. 잘 일반화되는 모델을 학습하려면 다음과 같은 데이터 세트 조건이 필요합니다.
- 예는 독립적이고 동일하게 분포되어야 합니다. 즉, 예가 서로 영향을 미칠 수 없다는 것을 멋진 방식으로 표현한 것입니다.
- 데이터 세트가 정상적입니다. 즉, 데이터 세트가 시간이 지남에 따라 크게 변경되지 않습니다.
- 데이터 세트 파티션의 분포가 동일합니다. 즉, 학습 세트의 예시가 검증 세트, 테스트 세트, 실제 데이터의 예시와 통계적으로 유사합니다.
다음 연습을 통해 위의 조건을 살펴보세요.
연습문제: 이해도 확인

챌린지 연습
승객이 특정 경로의 기차 티켓을 구매하기에 가장 적합한 날짜를 예측하는 모델을 만들고 있습니다. 예를 들어 모델은 사용자가 7월 23일에 출발하는 기차의 티켓을 7월 8일에 구매하도록 추천할 수 있습니다. 기차 회사는 다양한 요소를 고려하여 주로 현재 이용 가능한 좌석 수를 기준으로 매시간 가격을 업데이트합니다. 이는 다음과 같은 의미입니다.
- 이용 가능한 좌석이 많으면 일반적으로 티켓 가격이 낮습니다.
- 이용 가능한 좌석이 적은 경우 일반적으로 티켓 가격이 높습니다.
답변: 실제 모델이 피드백 루프에 어려움을 겪고 있습니다.
예를 들어 모델이 사용자에게 7월 8일에 티켓을 구매하도록 추천한다고 가정해 보겠습니다. 모델의 추천을 사용하는 일부 승객은 7월 8일 오전 8시 30분에 티켓을 구매합니다. 9시가 되면 기차 회사는 이용 가능한 좌석이 줄었으므로 가격을 인상합니다. 모델의 추천을 사용하는 라이더가 가격을 변경했습니다. 저녁이 되면 티켓 가격이 아침보다 훨씬 높을 수 있습니다.

