過学習とは、トレーニング セットと非常によく一致する(記憶する)モデルを作成した結果、新しいデータに対して正しい予測ができなくなることを意味します。過学習モデルは、実験では優れた性能を発揮するが、実世界では役に立たない発明に似ています。
図 11 では、各ジオメトリック シェイプが正方形の森内の木の位置を表しています。青いダイヤモンドは健康な木の場所を示し、オレンジ色の円は病気の木の場所を示します。

健康な木と病気の木を区別するために、線、曲線、楕円形など、任意の形を頭の中で描きます。次に、次の行を開いて、考えられる分離を 1 つ確認します。
図 12 に示す複雑な形状は、2 本の木を除くすべての木を正常に分類しました。シェイプをモデルと見なすと、これは素晴らしいモデルです。
本当にそうでしょうか?優れたモデルは、新しいサンプルを正常に分類します。図 13 は、同じモデルがテストセットの新しいサンプルに対して予測を行う場合の結果を示しています。

したがって、図 12 の複雑なモデルはトレーニング セットでは優れた結果を出しましたが、テストセットでは非常に悪い結果を出しました。これは、トレーニング セットデータにモデルが過学習している典型的なケースです。
適合、過学習、アンダーフィット
モデルは新しいデータに対して優れた予測を行う必要があります。つまり、新しいデータに「適合する」モデルを作成することを目標としています。
ご覧のとおり、過剰適合モデルはトレーニング セットでは優れた予測を行いますが、新しいデータでは予測が不十分です。アンダーフィットのモデルは、トレーニング データでさえ適切な予測を行いません。過剰適合モデルは、ラボでは優れたパフォーマンスを発揮するが、実世界ではそうではない製品に似ています。一方、アンダーフィット モデルは、ラボでも優れたパフォーマンスを発揮しない製品に似ています。

一般化は過学習の反対です。つまり、一般化が良好なモデルは、新しいデータに対して優れた予測を行います。目標は、新しいデータに適切に一般化できるモデルを作成することです。
過学習の検出
次の曲線は、過剰適合を検出するのに役立ちます。
- 損失曲線
- 一般化曲線
損失曲線は、モデルの損失とトレーニングの反復回数をプロットします。2 つ以上の損失曲線を示すグラフは、一般化曲線と呼ばれます。次の一般化曲線は、2 つの損失曲線を示しています。
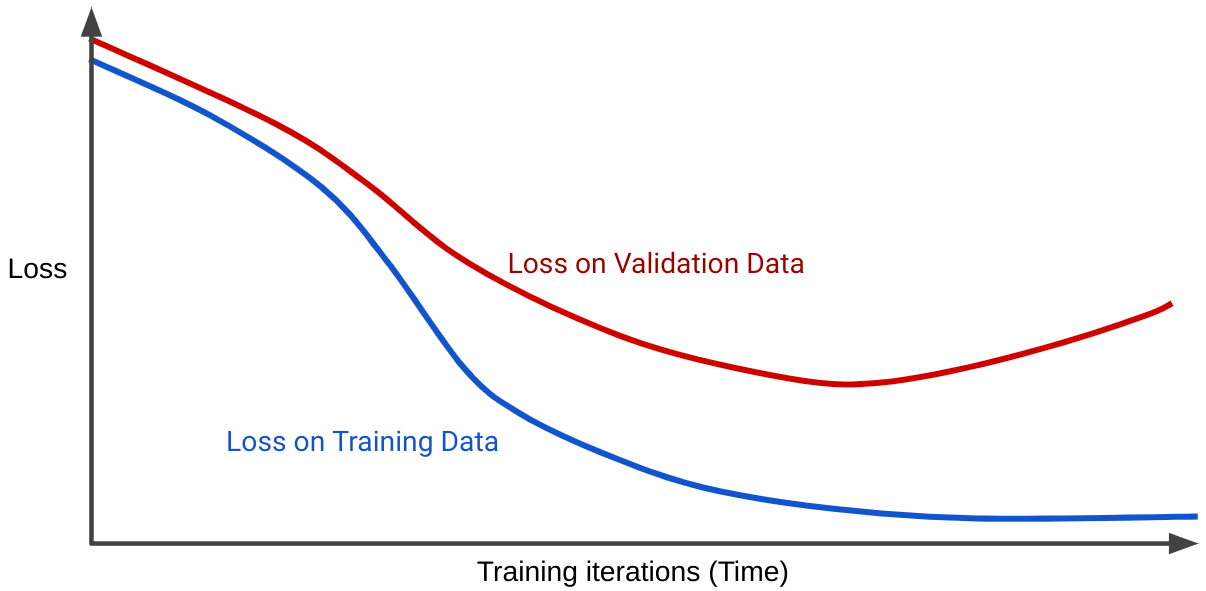
2 つの損失曲線は最初は同じように動作し、その後は分岐します。つまり、一定数の反復処理の後、トレーニング セットでは損失が減少または一定に保たれますが(収束)、検証セットでは増加します。これは過学習を示しています。
一方、適合性の高いモデルの一般化曲線には、形状が類似した 2 つの損失曲線が表示されます。
過学習の原因
大まかに言えば、過剰適合は次のいずれかまたは両方の問題によって発生します。
- トレーニング セットが実際のデータ(または検証セットやテストセット)を適切に表していない。
- モデルが複雑すぎる。
一般化の条件
モデルはトレーニング セットでトレーニングしますが、モデルの価値を実際にテストするのは、新しい例(特に実世界のデータ)に対する予測の精度です。モデルの開発中、テストセットは実世界のデータの代用として使用されます。一般化が良好なモデルをトレーニングするには、次のデータセット条件が必要です。
- 例は独立して同一に分布している必要があります。これは、例が互いに影響し合わないことを意味します。
- データセットは定常です。つまり、データセットは時間の経過とともに大幅に変化しません。
- データセット パーティションには同じ分布があります。つまり、トレーニング セットの例は、検証セット、テストセット、実際のデータの例と統計的に類似しています。
次の演習で、上記の条件を確認します。
演習: 理解度を確認する

チャレンジ エクササイズ
特定のルートの乗車券を購入するのに最適な日付を予測するモデルを作成しています。たとえば、7 月 23 日に出発する電車のチケットを 7 月 8 日に購入することをユーザーにおすすめするモデルが考えられます。鉄道会社は、さまざまな要因(主に現在の空席数)に基づいて、1 時間ごとに料金を更新します。具体的には、次のことが求められます。
- 空席が多い場合は、通常チケットの価格は低くなります。
- 残りの座席が少ない場合は、通常チケットの価格が高くなります。
回答: 現実世界のモデルはフィードバック ループに苦しんでいます。
たとえば、モデルがユーザーに 7 月 8 日にチケットを購入することを推奨しているとします。 モデルの最適化案を使用している一部の乗客は、7 月 8 日の午前 8 時 30 分にチケットを購入します。9 時になると、空席が減ったため、鉄道会社は料金を値上げします。モデルの推奨事項を使用している乗客は、料金を変更しています。夕方になると、チケットの価格が朝よりも大幅に高くなる可能性があります。

