Fazla Uydurma

Aşırı uyum, eğitim veri kümesiyle o kadar yakından eşleşen (ezberleyen) bir model oluşturmak anlamına gelir ki model yeni verilerle ilgili doğru tahminler yapamaz. Aşırı uyumlu bir model, laboratuvarda iyi performans gösteren ancak gerçek dünyada değersiz olan bir buluşa benzer.

Şekil 11'de her geometrik şeklin, kare şeklindeki bir ormandaki bir ağacın konumunu temsil ettiğini varsayalım. Mavi elmaslar sağlıklı ağaçların, turuncu daireler ise hasta ağaçların konumlarını gösterir.

Şekil 11. Bu şekilde yaklaşık 60 nokta vardır. Bu noktaların yarısı sağlıklı, yarısı ise hasta ağaçlardır. Sağlıklı ağaçlar çoğunlukla kuzeydoğu çeyreğindedir ancak kuzeybatı çeyreklerine de birkaç sağlıklı ağaç sızmıştır. Hastalıklı ağaçlar çoğunlukla güneydoğu çeyreğindedir ancak hastalıklı ağaçların birkaçı diğer çeyreklerde de bulunur.
Şekil 11. Eğitim veri kümesi: Kare şeklindeki bir ormandaki sağlıklı ve hastalıklı ağaçların konumları.

 

Sağlıklı ağaçları hasta ağaçlardan ayırmak için zihinsel olarak çizgi, eğri, oval gibi şekiller çizin. Ardından, olası bir ayırmayı incelemek için bir sonraki satırı genişletin.

Şekil 12'de gösterilen karmaşık şekiller, ağaçların ikisi dışında hepsini başarıyla sınıflandırdı. Şekilleri bir model olarak düşünürsek bu harika bir modeldir.

Yoksa mümkün mü dersiniz? Gerçekten mükemmel bir model, yeni örnekleri başarıyla kategorize eder. Şekil 13, aynı model test veri kümesindeki yeni örneklerle ilgili tahminde bulunduğunda ne olacağını gösterir:

Şekil 13. Şekil 12'de gösterilen modelin üzerine yerleştirilmiş yeni bir grup sağlıklı ve hasta ağaç. Model, ağaçların çoğunu yanlış sınıflandırıyor.
Şekil 13. Test grubu: Hasta ağaçları sağlıklı ağaçlardan ayırt etmek için kullanılan karmaşık bir model.

 

Bu nedenle, Şekil 12'de gösterilen karmaşık model, eğitim veri kümesinde mükemmel bir performans gösterdi ancak test veri kümesinde oldukça kötü bir performans gösterdi. Bu, bir modelin eğitim veri kümesine aşırı uyum sağladığı klasik bir durumdur.

Uyumlu hale getirme, fazla uyumlu hale getirme ve yetersiz uyumlu hale getirme

Model, yeni verilerle ilgili iyi tahminler yapmalıdır. Yani yeni verilere "uyan" bir model oluşturmayı hedefliyorsunuz.

Gördüğünüz gibi, aşırı uyumlu bir model eğitim veri kümesinde mükemmel tahminler yaparken yeni verilerde kötü tahminler yapar. Yetersiz uyumlu bir model, eğitim verileri hakkında bile iyi tahminler yapamaz. Aşırı uyumlu bir model, laboratuvarda iyi ancak gerçek dünyada kötü performans gösteren bir ürün gibidir. Yetersiz uyumlu bir model ise laboratuvarda bile iyi performans göstermeyen bir ürün gibidir.

Şekil 14. Kartezyen nokta grafiği. X ekseni "eğitim veri kümesindeki tahminlerin kalitesi" olarak etiketlenmiştir. Y ekseni "gerçek dünyadaki verilere göre tahminlerin kalitesi" olarak etiketlenmiştir. Bir eğri, orijinde başlar ve kademeli olarak yükselir, ancak daha sonra aynı hızla düşer. Eğrinin sol alt kısmı (gerçek verilerdeki tahminlerin düşük kalitesi ve eğitim veri kümesindeki tahminlerin düşük kalitesi) "yeterince eğitilmemiş modeller" olarak etiketlenmiştir. Eğrinin sağ alt kısmı ("gerçek verilerde düşük kaliteli, eğitim veri kümesinde yüksek kaliteli tahminler"), "aşırı uyumlu modeller" olarak etiketlenir. Eğrinin zirvesi ("gerçek verilerdeki tahminlerin yüksek kalitesi ve eğitim veri kümesindeki tahminlerin orta kalitesi") "uygun modeller" olarak etiketlenir.
Şekil 14. Yetersiz uyumlu, uyumlu ve fazla uyumlu modeller.

 

Genelleştirme, fazla uyumun tam tersidir. Yani iyi genelleme yapan bir model, yeni verilerle ilgili iyi tahminler yapar. Hedefiniz, yeni verilere iyi genelleme yapan bir model oluşturmaktır.

Fazla uyumu tespit etme

Aşağıdaki eğriler, aşırı uyumu tespit etmenize yardımcı olur:

  • kayıp eğrileri
  • genelleştirme eğrileri

Kayıp eğrisi, bir modelin kaybını eğitim iterasyonlarının sayısına göre gösterir. İki veya daha fazla kayıp eğrisini gösteren bir grafiğe genelleştirme eğrisi denir. Aşağıdaki genelleme eğrisinde iki kayıp eğrisi gösterilmektedir:

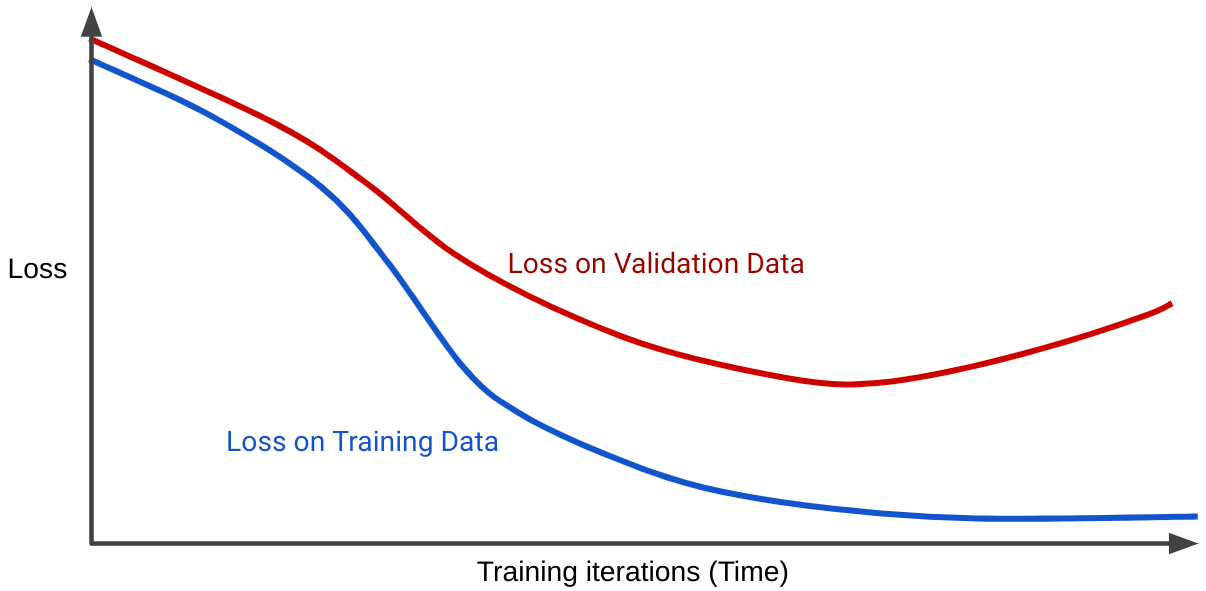
Şekil 15. Eğitim veri kümesinin kayıp işlevi kademeli olarak azalır. Doğrulama veri kümesinin kayıp işlevi de azalır ancak belirli sayıda iterasyondan sonra yükselmeye başlar.
Şekil 15. Aşırı uyumu güçlü bir şekilde ima eden bir genelleme eğrisi.

 

İki kayıp eğrisinin başlangıçta benzer şekilde davranıp daha sonra farklılaştığına dikkat edin. Yani belirli sayıda iterasyondan sonra kayıp, eğitim kümesi için azalır veya sabit kalır (yakınlaşır) ancak doğrulama kümesi için artar. Bu, fazla uyum olduğunu gösterir.

Buna karşılık, iyi uyumlu bir model için genelleme eğrisi, benzer şekillere sahip iki kayıp eğrisi gösterir.

Aşırı uyum sağlamaya ne neden olur?

Aşırı uyum, genel olarak aşağıdaki sorunlardan biri veya ikisinden kaynaklanır:

  • Eğitim kümesi, gerçek hayat verilerini (veya doğrulama kümesini ya da test kümesini) yeterince temsil etmiyor.
  • Model çok karmaşık.

Genelleştirme koşulları

Bir model, eğitim veri kümesinde eğitilir ancak modelin değerini belirleyen gerçek test, yeni örneklerde (özellikle gerçek dünyadaki verilerde) ne kadar iyi tahminde bulunduğudur. Test kümeniz, model geliştirirken gerçek dünya verileri için proxy görevi görür. İyi genelleme yapan bir model eğitmek için aşağıdaki veri kümesi koşullarını karşılamanız gerekir:

  • Örnekler bağımsız ve aynı şekilde dağıtılmış olmalıdır. Bu, örneklerinizin birbirini etkileyemeyeceğinin süslü bir ifadesidir.
  • Veri kümesi sabit olduğundan zaman içinde önemli ölçüde değişmez.
  • Veri kümesi bölümleri aynı dağılıma sahiptir. Yani eğitim kümesindeki örnekler, doğrulama kümesindeki, test kümesindeki ve gerçek verilerdeki örneklere istatistiksel olarak benzerdir.

Aşağıdaki alıştırmalar aracılığıyla önceki koşulları keşfedin.

Alıştırmalar: Öğrendiklerinizi test edin

Aşağıdaki veri kümesi bölümlerini göz önünde bulundurun.
Üç parçaya bölünmüş yatay bir çubuk: Çubuğun% 70'i eğitim kümesi, %15'i doğrulama kümesi ve %15'i test kümesidir.
Eğitim kümesindeki örneklerin doğrulama kümesindeki ve test kümesindeki örneklere benzer bir istatistiksel dağılıma sahip olmasını sağlamak için ne yapmalısınız?
Veri kümesindeki örnekleri bölümlendirmeden önce kapsamlı bir şekilde karıştırın.
Evet. Örneklerin iyi bir şekilde karıştırılması, bölümlerin istatistiksel olarak benzer olma olasılığını çok daha artırır.
Örnekleri en eskiden en yeniye göre sıralayın.
Veri kümesindeki örnekler sabit değilse sıralama, bölümleri daha benzer hale getirir.
Hiçbir işlem yapmamayı tercih edebilirsiniz. Yeterli sayıda örnek verildiğinde ortalamalar yasası, dağılımların istatistiksel olarak benzer olmasını doğal olarak sağlar.
Maalesef bu mümkün değil. Veri kümesinin belirli bölümlerindeki örnekler, diğer bölümlerdeki örneklerden farklı olabilir.
Bir akış hizmeti, önümüzdeki üç yıl içinde yayınlanabilecek yeni televizyon programlarının popülerliğini tahmin edecek bir model geliştiriyor. Akış hizmeti, modeli önceki on yıla ait yüz milyonlarca örnek içeren bir veri kümesinde eğitmeyi planlıyor. Bu modelde bir sorun yaşanır mı?
Muhtemelen. İzleyicilerin beğenileri, geçmişteki davranışların tahmin edemeyeceği şekilde değişir.
Evet. İzleyicilerin beğenileri sabit değildir. Bu değerler sürekli olarak değişir.
Kesinlikle hayır. Veri kümesi, iyi tahminler oluşturacak kadar büyük olmalıdır.
Maalesef izleyicilerin beğenileri sabit değildir.
Muhtemelen karşılaşmazsınız. İzleyicilerin zevkleri, tahmin edilebilir şekilde döngüsel bir şekilde değişir. On yıllık veriler, modelin gelecekteki trendler hakkında iyi tahminler yapmasına olanak tanır.
Eğlencenin belirli yönleri biraz döngüsel olsa da geçmiş eğlence geçmişinden eğitilmiş bir modelin önümüzdeki birkaç yılla ilgili tahminlerde bulunması neredeyse kesin olarak zor olacaktır.
Bir model, hava durumu mevsime göre önemli ölçüde değişen bir şehirde bir yıl boyunca toplanan hava durumu verilerine (sıcaklık, çiy noktası ve yağış) göre kullanıcıların bir mil yürümesinin ne kadar süreceğini tahmin etmeyi amaçlar. Hava durumu ölçümleri mevsime göre önemli ölçüde değişse bile bu veri kümesinden bir model oluşturup test edebilir misiniz?
Evet
Evet, bu veri kümesinden model oluşturmak ve test etmek mümkündür. Tek yapmanız gereken, verilerin eşit şekilde bölümlendirildiğinden emin olmaktır. Böylece, dört sezonun verileri farklı bölümlere eşit şekilde dağıtılır.
Hayır
Bu veri kümesinin sıcaklık, çiy noktası ve yağışla ilgili yeterli örnek içerdiğini varsayarsak bu veri kümesinden bir model oluşturup test edebilirsiniz. Dört sezonun verilerinin eşit olarak farklı bölümlere dağıtılması için verilerin eşit şekilde bölümlendirildiğinden emin olmanız yeterlidir.

Zorluk alıştırması

Kullanıcıların belirli bir rota için tren bileti satın almaları için ideal tarihi tahmin eden bir model oluşturuyorsunuz. Örneğin, model kullanıcıların 23 Temmuz'da hareket edecek bir tren için biletlerini 8 Temmuz'da satın almalarını önerebilir. Tren şirketi, fiyatları çeşitli faktörlere (özellikle de mevcut koltuk sayısına) göre saatlik olarak günceller. Yani:

  • Çok sayıda koltuk varsa bilet fiyatları genellikle düşüktür.
  • Çok az koltuk varsa bilet fiyatları genellikle yüksektir.
Modeliniz, doğrulama ve test veri kümelerinde düşük kayıp gösterir ancak bazen gerçek dünya verilerinde kötü tahminler yapar. Neden?
Yanıtı görmek için burayı tıklayın
Önceki
Genelleme (5 dk.)
Sonraki
Model karmaşıklığı (10 dk.)