El descenso de gradientes es una técnica matemática que encuentra de forma iterativa los pesos y el sesgo que producen el modelo con la pérdida más baja. El descenso de gradientes encuentra el mejor peso y sesgo repitiendo el siguiente proceso para una cantidad de iteraciones definidas por el usuario.
El modelo comienza el entrenamiento con pesos y sesgos aleatorios cercanos a cero y, luego, repite los siguientes pasos:
Calcula la pérdida con el peso y el sesgo actuales.
Determina la dirección en la que se deben mover los pesos y la desviación para reducir la pérdida.
Mueve los valores de peso y sesgo una pequeña cantidad en la dirección que reduce la pérdida.
Vuelve al paso uno y repite el proceso hasta que el modelo no pueda reducir más la pérdida.
En el siguiente diagrama, se describen los pasos iterativos que realiza el descenso de gradientes para encontrar los pesos y el sesgo que producen el modelo con la pérdida más baja.
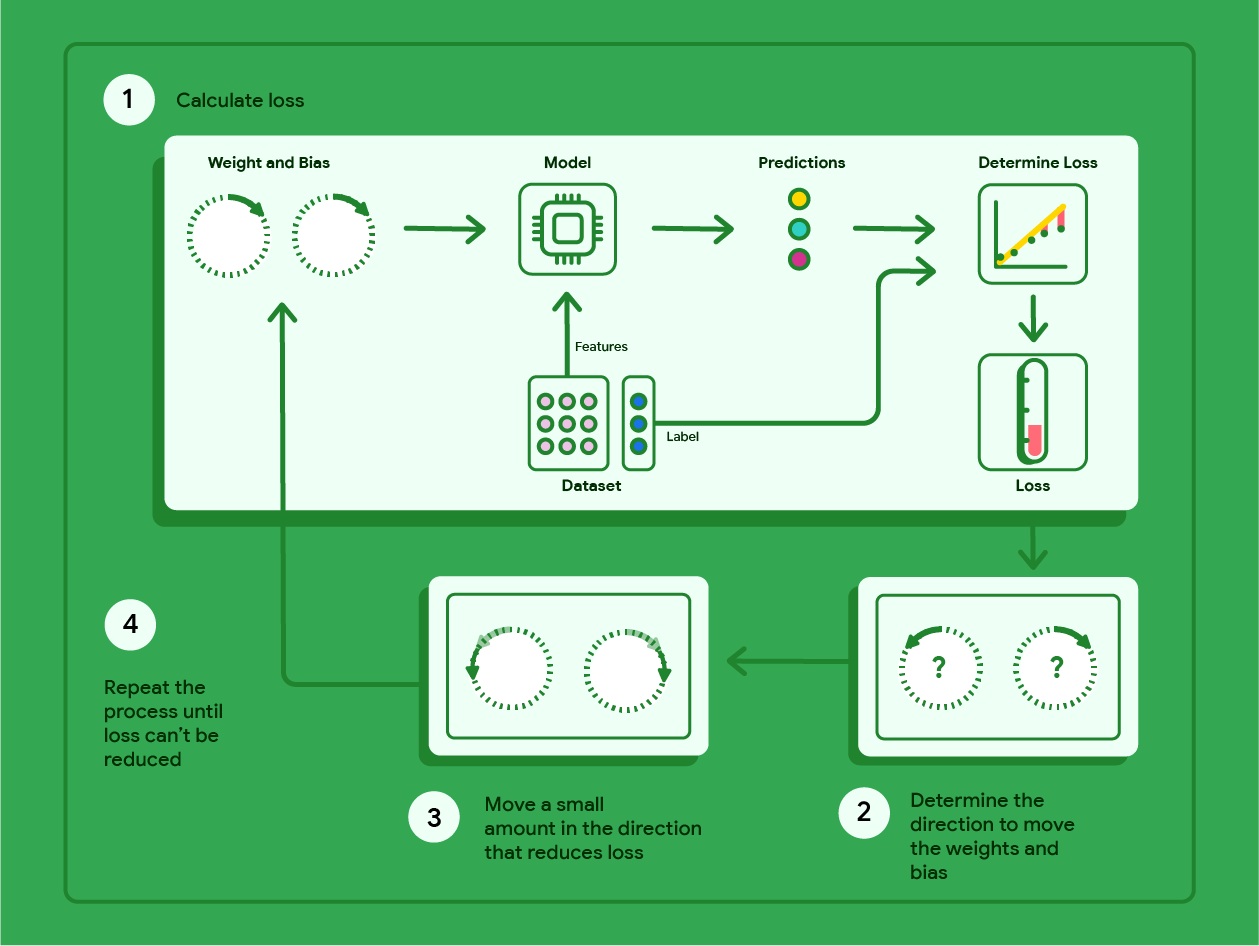
Figura 11: El descenso de gradientes es un proceso iterativo que encuentra los pesos y el sesgo que producen el modelo con la pérdida más baja.
Haz clic en el ícono de signo más para obtener más información sobre las matemáticas detrás del descenso del gradiente.
En un nivel concreto, podemos analizar los pasos del descenso de gradientes con un conjunto de datos pequeño de siete ejemplos para el peso de un automóvil en libras y su clasificación de millas por galón:
| Libras en miles (característica) | Millas por galón (etiqueta) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- El modelo comienza el entrenamiento estableciendo el peso y el sesgo en cero:
- Calcula la pérdida del ECM con los parámetros actuales del modelo:
- Calcula la pendiente de la tangente a la función de pérdida en cada peso y sesgo:
- Mueve una pequeña cantidad en la dirección de la pendiente negativa para obtener el siguiente peso y sesgo. Por ahora, definiremos arbitrariamente la "cantidad pequeña" como 0.01:
Haz clic en el ícono de signo más para obtener información sobre cómo calcular la pendiente.
Para obtener la pendiente de las rectas tangentes al peso y al sesgo, derivamos la función de pérdida con respecto al peso y al sesgo, y, luego, resolvemos las ecuaciones.
Escribiremos la ecuación para hacer una predicción de la siguiente manera:
$ f_{w,b}(x) = (w*x)+b $.
Escribiremos el valor real como: $ y $.
Calcularemos el MSE con la siguiente fórmula:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
donde $i$ representa el $i$-ésimo ejemplo de entrenamiento y $M$ representa
la cantidad de ejemplos.
La derivada de la función de pérdida con respecto al peso se escribe de la siguiente manera:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
y se evalúa como:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
Primero, sumamos cada valor predicho menos el valor real y, luego, lo multiplicamos por dos veces el valor del atributo. Luego, dividimos la suma por la cantidad de ejemplos. El resultado es la pendiente de la línea tangente al valor del peso.
Si resolvemos esta ecuación con un peso y un sesgo iguales a cero, obtenemos -119.7 para la pendiente de la línea.
Derivada del sesgo
La derivada de la función de pérdida con respecto al sesgo se escribe de la siguiente manera:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
y se evalúa como:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
Primero, sumamos cada valor predicho menos el valor real y, luego, lo multiplicamos por dos. Luego, dividimos la suma entre la cantidad de ejemplos. El resultado es la pendiente de la línea tangente al valor del sesgo.
Si resolvemos esta ecuación con un peso y una ordenada al origen iguales a cero, obtenemos -34.3 para la pendiente de la línea.
Usa el nuevo peso y sesgo para calcular la pérdida y repetir el proceso. Si completamos el proceso durante seis iteraciones, obtendríamos los siguientes pesos, sesgos y pérdidas:
| Iteración | Peso | Sesgo | Pérdida (ECM) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
Puedes ver que la pérdida disminuye con cada peso y sesgo actualizados. En este ejemplo, nos detuvimos después de seis iteraciones. En la práctica, un modelo se entrena hasta que converge. Cuando un modelo converge, las iteraciones adicionales no reducen más la pérdida porque el descenso de gradientes encontró los pesos y el sesgo que casi minimizan la pérdida.
Si el modelo continúa entrenándose después de la convergencia, la pérdida comienza a fluctuar en cantidades pequeñas a medida que el modelo actualiza continuamente los parámetros en torno a sus valores más bajos. Esto puede dificultar la verificación de que el modelo realmente haya convergido. Para confirmar que el modelo convergió, deberás continuar con el entrenamiento hasta que la pérdida se estabilice.
Curvas de pérdida y convergencia del modelo
Cuando entrenas un modelo, a menudo observas una curva de pérdida para determinar si el modelo convergió. La curva de pérdida muestra cómo cambia la pérdida a medida que se entrena el modelo. A continuación, se muestra cómo se ve una curva de pérdida típica. La pérdida se muestra en el eje Y y las iteraciones en el eje X:
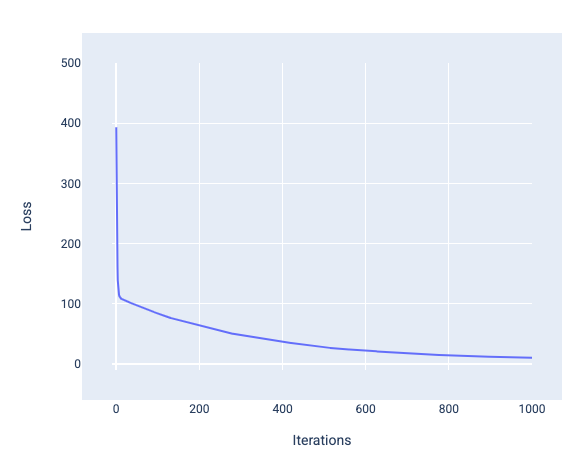
Figura 12: Curva de pérdida que muestra la convergencia del modelo alrededor de la iteración número 1,000.
Puedes ver que la pérdida disminuye drásticamente durante las primeras iteraciones y, luego, se reduce de forma gradual antes de estabilizarse alrededor de la iteración número 1,000. Después de 1,000 iteraciones, podemos tener la certeza de que el modelo convergió.
En las siguientes figuras, dibujamos el modelo en tres puntos durante el proceso de entrenamiento: el comienzo, el medio y el final. Visualizar el estado del modelo en instantáneas durante el proceso de entrenamiento consolida la vinculación entre la actualización de los pesos y el sesgo, la reducción de la pérdida y la convergencia del modelo.
En las figuras, usamos los pesos y la desviación derivados en una iteración particular para representar el modelo. En el gráfico con los puntos de datos y la instantánea del modelo, las líneas de pérdida azules del modelo a los puntos de datos muestran la cantidad de pérdida. Cuanto más largas sean las líneas, mayor será la pérdida.
En la siguiente figura, podemos ver que, alrededor de la segunda iteración, el modelo no sería bueno para hacer predicciones debido a la gran cantidad de pérdida.
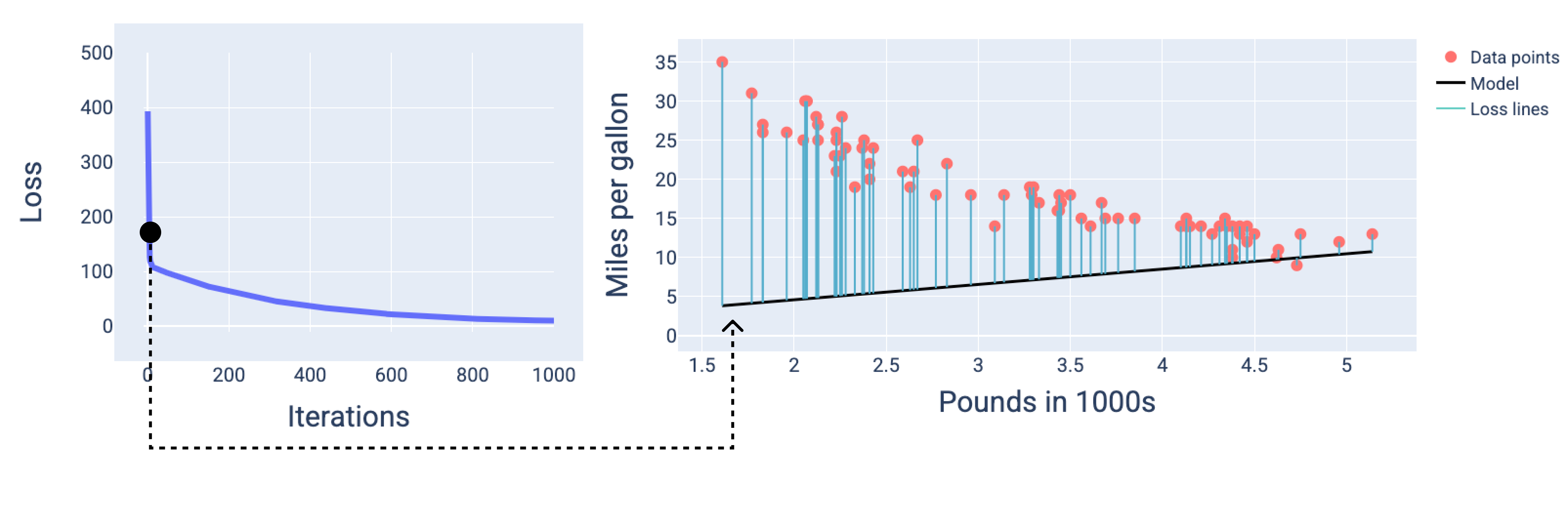
Figura 13: Curva de pérdida y una instantánea del modelo al comienzo del proceso de entrenamiento.
Alrededor de la iteración 400, podemos ver que el descenso del gradiente encontró el peso y el sesgo que producen un mejor modelo.
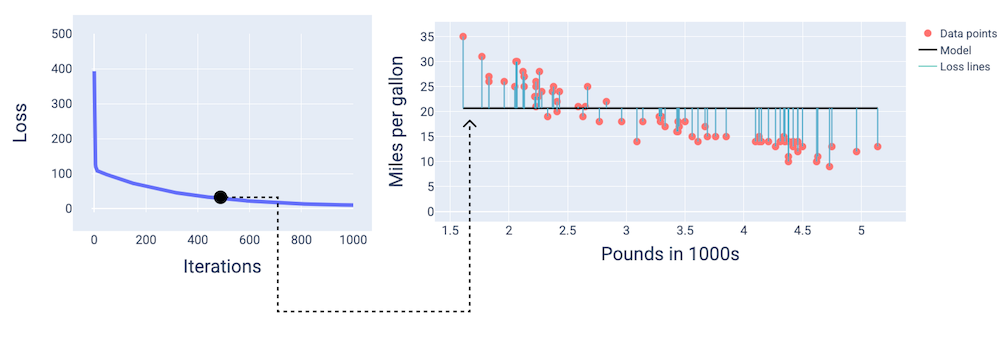
Figura 14. Curva de pérdida y captura de pantalla del modelo a mitad del entrenamiento.
Y,alrededor de la iteración número 1, 000, podemos ver que el modelo convergió y produjo un modelo con la pérdida más baja posible.
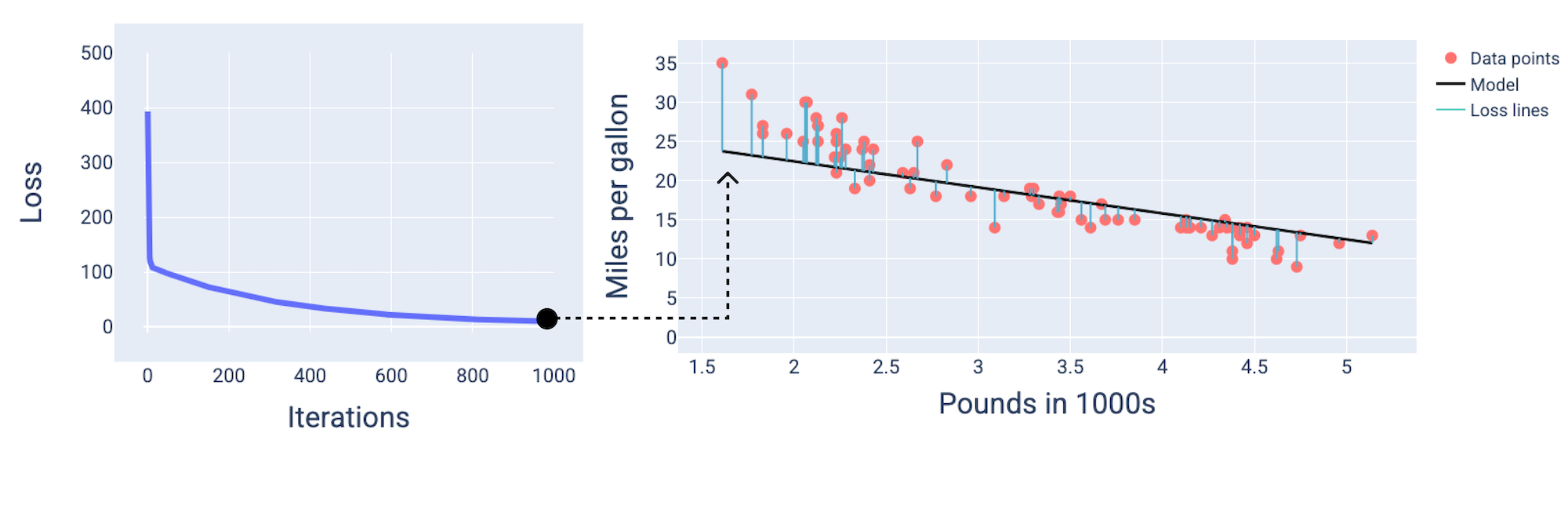
Figura 15. Curva de pérdida y una instantánea del modelo cerca del final del proceso de entrenamiento.
Ejercicio: Comprueba tus conocimientos
Convergencia y funciones convexas
Las funciones de pérdida para los modelos lineales siempre producen una superficie convexa. Como resultado de esta propiedad, cuando un modelo de regresión lineal converge, sabemos que encontró los pesos y la desviación que producen la pérdida más baja.
Si graficamos la superficie de pérdida de un modelo con una sola característica, podemos ver su forma convexa. A continuación, se muestra la superficie de pérdida para un conjunto de datos hipotético de millas por galón. El peso está en el eje X, el sesgo en el eje Y y la pérdida en el eje Z:
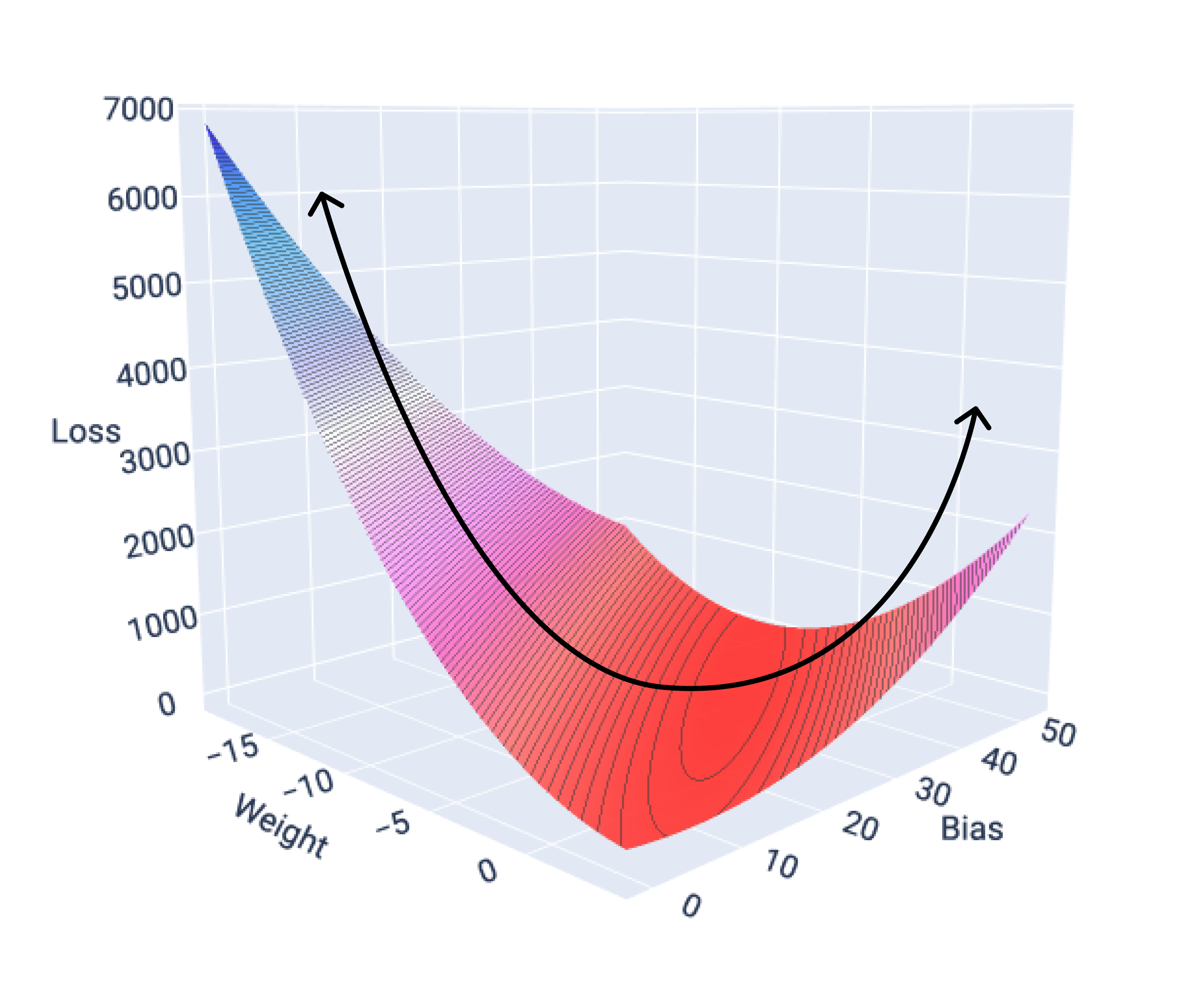
Figura 16: Superficie de pérdida que muestra su forma convexa.
En este ejemplo, un peso de -5.44 y un sesgo de 35.94 producen la pérdida más baja en 5.54:
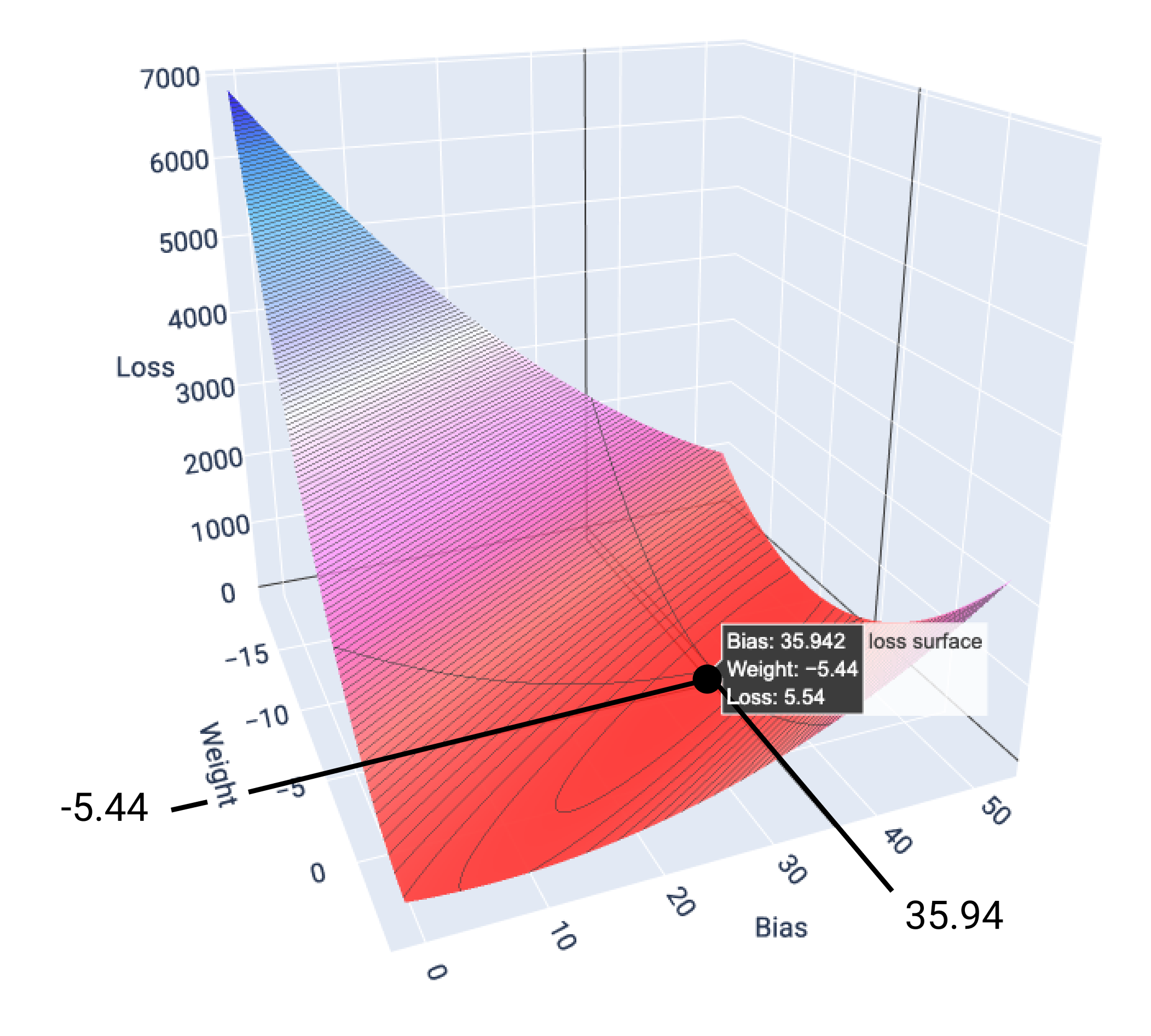
Figura 17: Superficie de pérdida que muestra los valores de peso y sesgo que producen la pérdida más baja.
Un modelo lineal converge cuando encuentra la pérdida mínima. Por lo tanto, las iteraciones adicionales solo hacen que el descenso del gradiente mueva los valores de peso y sesgo en cantidades muy pequeñas alrededor del mínimo. Si graficáramos los pesos y los puntos de sesgo durante el descenso del gradiente, los puntos se verían como una pelota que rueda cuesta abajo y, finalmente, se detiene en el punto en el que ya no hay pendiente descendente.
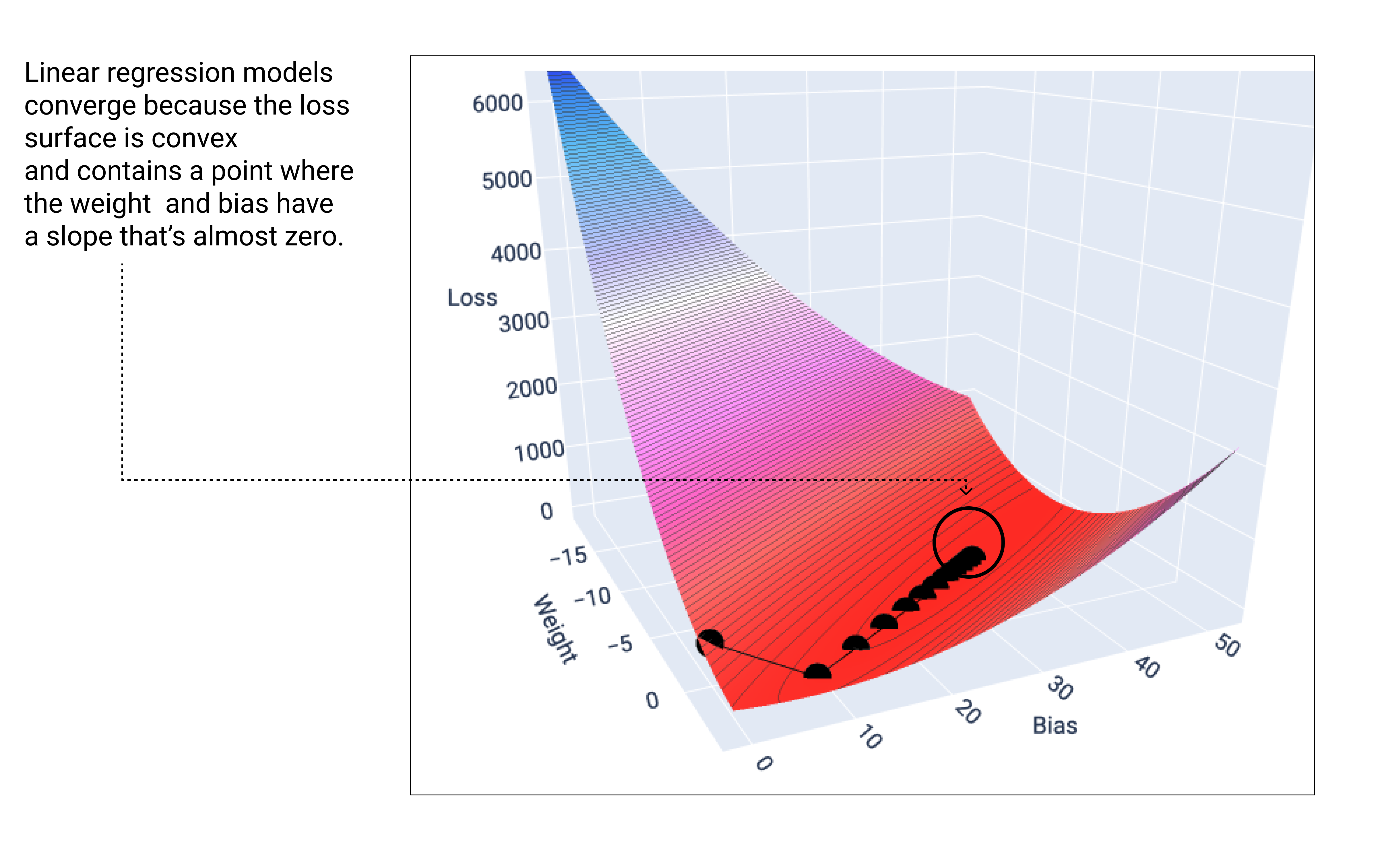
Figura 18: Gráfico de pérdida que muestra los puntos de descenso del gradiente que se detienen en el punto más bajo del gráfico.
Observa que los puntos de pérdida negros crean la forma exacta de la curva de pérdida: una disminución pronunciada antes de descender gradualmente hasta alcanzar el punto más bajo en la superficie de pérdida.
Es importante tener en cuenta que el modelo casi nunca encuentra el mínimo exacto para cada peso y sesgo, sino que encuentra un valor muy cercano a él. También es importante tener en cuenta que el mínimo para los pesos y la desviación no corresponde a una pérdida cero, sino solo a un valor que produce la pérdida más baja para ese parámetro.
Con los valores de peso y sesgo que producen la pérdida más baja (en este caso, un peso de -5.44 y un sesgo de 35.94), podemos graficar el modelo para ver qué tan bien se ajusta a los datos:
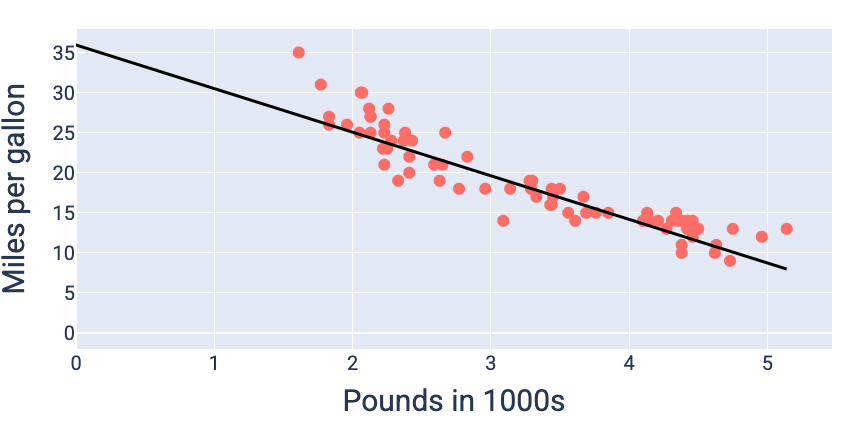
Figura 19: Modelo graficado con los valores de peso y sesgo que producen la pérdida más baja.
Este sería el mejor modelo para este conjunto de datos, ya que ningún otro valor de peso y sesgo produce un modelo con una pérdida menor.
