La descente de gradient est une technique mathématique qui trouve de manière itérative les pondérations et les biais qui produisent le modèle présentant la perte la plus faible. La descente de gradient trouve le meilleur poids et le meilleur biais en répétant le processus suivant pour un certain nombre d'itérations définies par l'utilisateur.
Le modèle commence l'entraînement avec des pondérations et des biais aléatoires proches de zéro, puis répète les étapes suivantes:
Calculez la perte à l'aide de la pondération et du biais actuels.
Déterminez la direction dans laquelle déplacer les poids et les biais qui réduisent la perte.
Déplacez les valeurs de poids et de biais d'une petite quantité dans la direction qui réduit la perte.
Revenez à l'étape 1 et répétez le processus jusqu'à ce que le modèle ne puisse plus réduire la perte.
Le schéma ci-dessous décrit les étapes itératives de la descente de gradient pour identifier les pondérations et les biais à l'origine du modèle présentant la perte la plus faible.
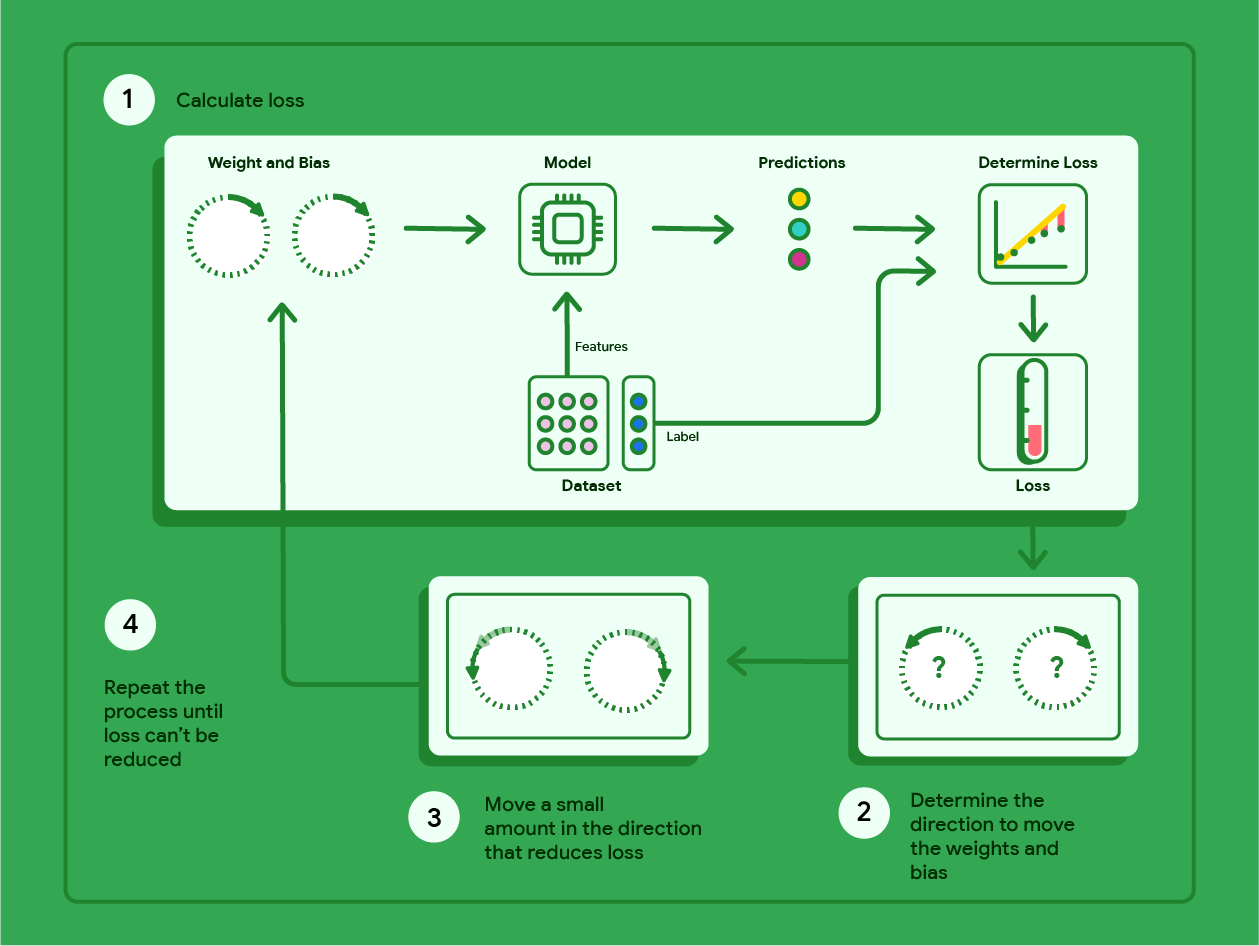
Figure 12. La descente du gradient est un processus itératif qui trouve les pondérations et les biais qui produisent le modèle avec la perte la plus faible.
Cliquez sur l'icône Plus pour en savoir plus sur les calculs derrière la descente de gradient.
Concrètement, nous pouvons parcourir les étapes de la descente de gradient à l'aide d'un petit ensemble de données comprenant sept exemples de poids d'une voiture en livres et sa cote en miles par gallon:
| Livres par milliers (fonctionnalité) | Miles par gallon (libellé) |
|---|---|
| 3.5 | 18 |
| 3,69 | 15 |
| 3.44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
- Le modèle commence l'entraînement en définissant la pondération et le biais sur zéro:
- Calculez la perte MSE avec les paramètres du modèle actuels:
- Calculez la pente de la tangente à la fonction de perte à chaque poids et au biais:
- Déplacez-vous d'une petite quantité dans la direction de la pente négative pour obtenir le poids et le biais suivants. Pour l'instant, nous allons définir arbitrairement la "petite somme" sur 0,01:
Cliquez sur l'icône Plus pour en savoir plus sur le calcul de la pente.
Pour obtenir la pente des lignes tangentes au poids et au biais, nous prenons la dérivée de la fonction de perte par rapport au poids et au biais, puis nous résolvons les équations.
Nous allons écrire l'équation de prédiction comme suit:
$ f_{w,b}(x) = (w*x)+b $.
Nous allons écrire la valeur réelle sous la forme: $ y $.
Nous allons calculer la MSE à l'aide de la formule suivante:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
où $i$ représente l'exemple d'entraînement $i$ et $M$ le nombre d'exemples.
La dérivée de la fonction de perte par rapport à la pondération est écrite comme suit:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
et renvoie la valeur suivante:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
Nous commençons par additionner chaque valeur prédite moins la valeur réelle, puis nous la multiplions par deux fois la valeur de l'élément géographique. Nous divisons ensuite la somme par le nombre d'exemples. Le résultat est la pente de la ligne tangente à la valeur de la pondération.
Si nous résolvons cette équation avec une pondération et un biais égaux à zéro, nous obtenons -119,7 pour la pente de la droite.
Dérivée des biais
La dérivée de la fonction de perte par rapport au biais s'écrit comme suit:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
et donne la valeur suivante:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
Nous commençons par additionner chaque valeur prédite moins la valeur réelle, puis nous la multiplions par deux. Nous divisons ensuite la somme par le nombre d'exemples. Le résultat est la pente de la ligne tangente à la valeur du biais.
Si nous résolvons cette équation avec une pondération et un biais égaux à zéro, nous obtenons -34,3 pour la pente de la droite.
Utilisez la nouvelle pondération et le nouveau biais pour calculer la perte et la répétition. En en terminant le processus pour six itérations, nous obtiendrions les pondérations, biais et pertes suivants:
| Itération | Poids | Biais | Perte (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303,71 |
| 2 | 1.2 | 0,34 | 170.67 |
| 3 | 2,75 | 0.59 | 67,3 |
| 4 | 3.17 | 0.72 | 50,63 |
| 5 | 3,47 | 0.82 | 42.1 |
| 6 | 3,68 | 0,9 | 37,74 |
Vous pouvez constater que la perte diminue à chaque mise à jour des pondérations et des biais. Dans cet exemple, nous nous sommes arrêtés après six itérations. En pratique, un modèle est entraîné jusqu'à ce qu'il converge. Lorsqu'un modèle converge, les itérations supplémentaires ne réduisent pas davantage la perte, car la descente de gradient a identifié les pondérations et les biais qui minimisent presque la perte.
Si le modèle continue de s'entraîner après la convergence, la perte commence à fluctuer légèrement, car le modèle met constamment à jour les paramètres autour de leurs valeurs les plus basses. Cela peut rendre difficile de vérifier que le modèle a effectivement convergé. Pour confirmer que le modèle a convergé, vous devez poursuivre l'entraînement jusqu'à ce que la perte se stabilise.
Convergence du modèle et courbes de perte
Lorsque vous entraînez un modèle, vous examinez souvent une courbe de perte pour déterminer si le modèle a convergé. La courbe de perte montre comment la perte change à mesure que le modèle s'entraîne. Voici à quoi ressemble une courbe de perte typique. La perte est représentée sur l'axe des y et les itérations sur l'axe des x:
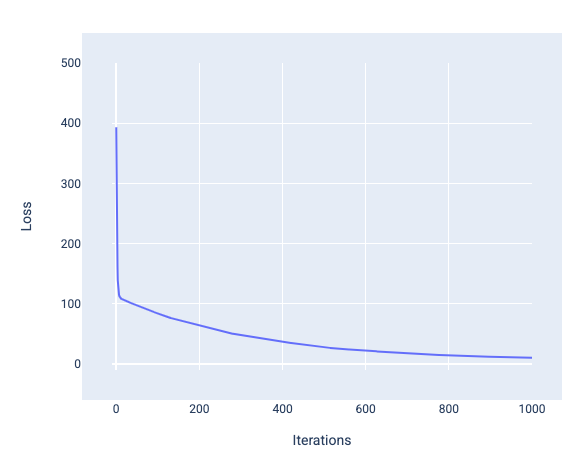
Figure 13. Courbe de perte montrant la convergence du modèle autour de la 1 000e itération.
Vous pouvez constater que la perte diminue considérablement au cours des premières itérations, puis diminue progressivement avant de s'aplatir vers la 1 000e itération. Après 1 000 itérations, nous pouvons être presque certains que le modèle a convergé.
Dans les figures suivantes, le modèle est dessiné à trois points du processus d'entraînement: le début, le milieu et la fin. La visualisation de l'état du modèle lors des instantanés pendant le processus d'entraînement renforce le lien entre la mise à jour des poids et des biais, la réduction des pertes et la convergence du modèle.
Dans les figures, nous utilisons les pondérations et le biais dérivés à une itération donnée pour représenter le modèle. Dans le graphique contenant les points de données et l'instantané du modèle, les lignes de perte bleues entre le modèle et les points de données indiquent la quantité de perte. Plus les droites sont longues, plus il y a de perte.
Dans la figure suivante, nous pouvons voir qu'autour de la deuxième itération, le modèle ne serait pas en mesure de faire de bonnes prédictions en raison de la forte perte.
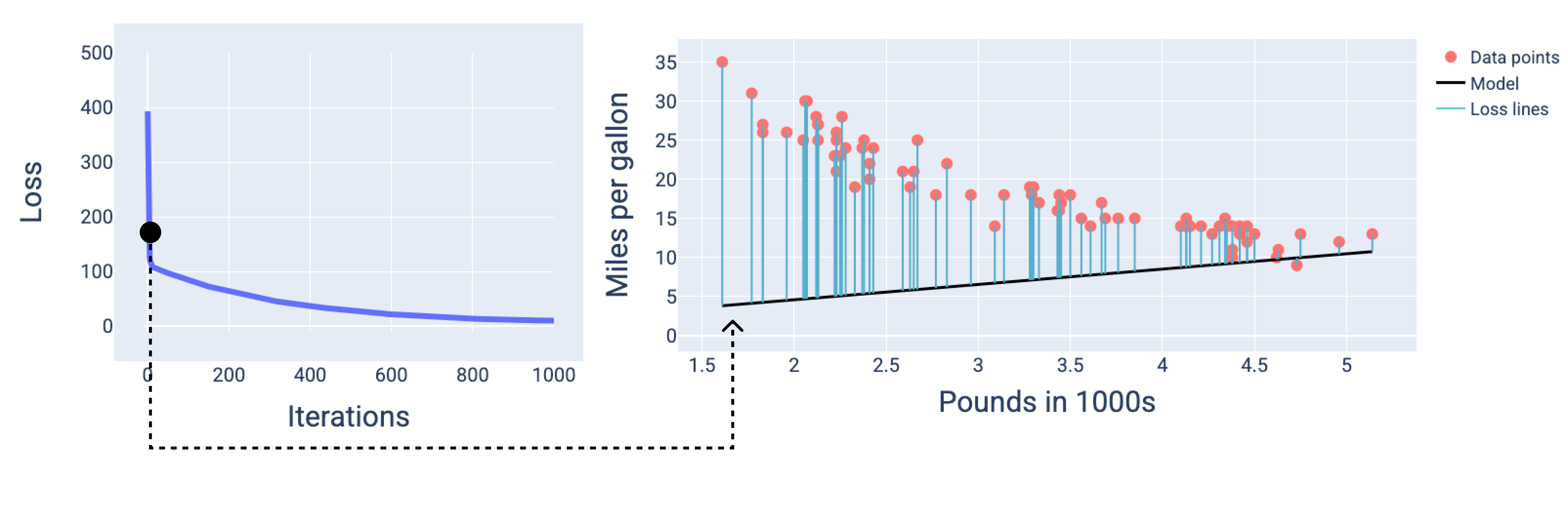
Figure 14. Courbe de perte et instantané du modèle au début du processus d'entraînement.
Vers la 400e itération, nous pouvons voir que la descente du gradient a trouvé les poids et les biais qui produisent un meilleur modèle.
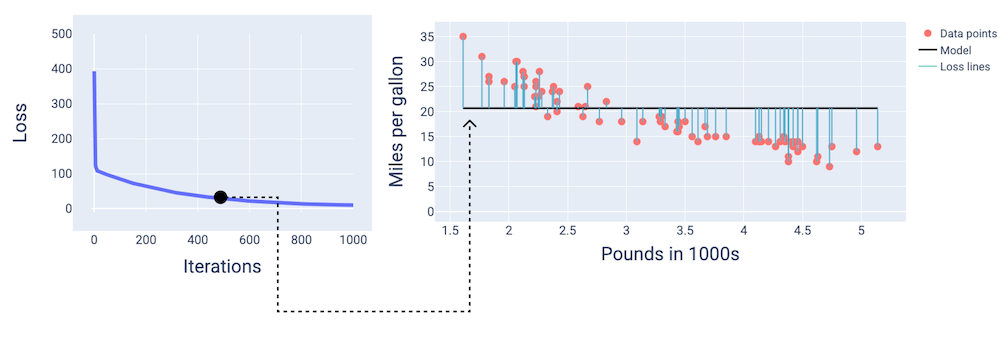
Figure 15. Courbe de perte et instantané du modèle vers le milieu de l'entraînement.
Vers la 1 000e itération, nous pouvons voir que le modèle a convergé, produisant un modèle avec la perte la plus faible possible.
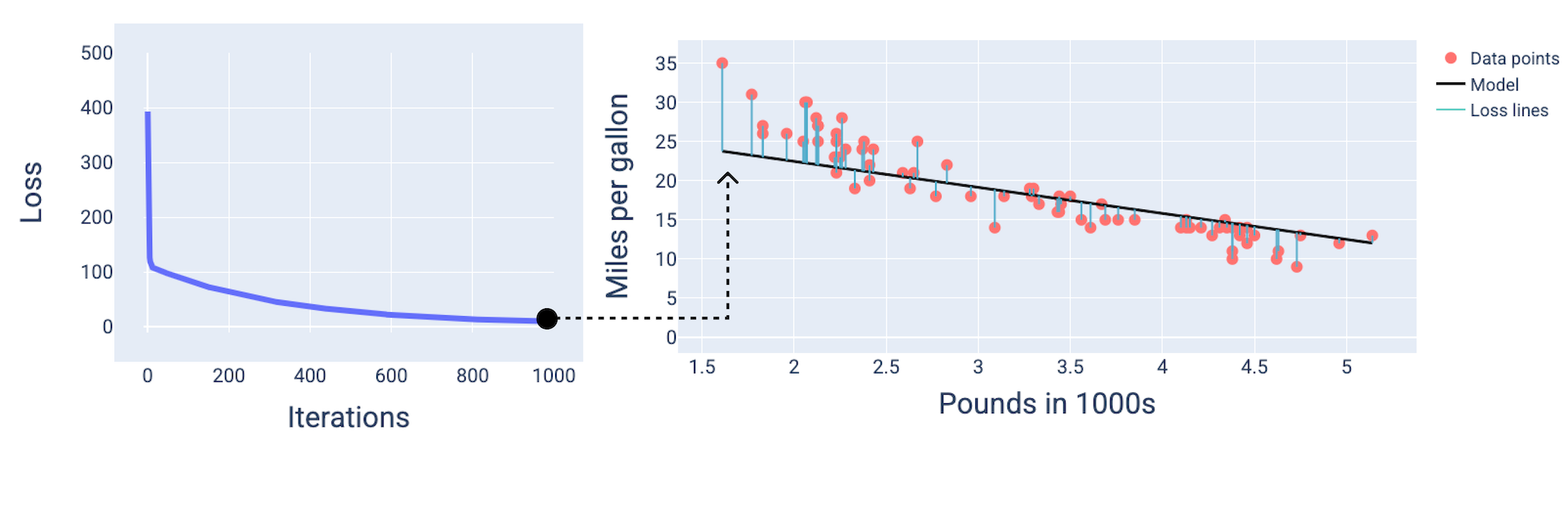
Figure 16 : Courbe de perte et instantané du modèle vers la fin du processus d'entraînement.
Exercice : Vérifiez votre compréhension
Convergence et fonctions convexes
Les fonctions de perte des modèles linéaires génèrent toujours une surface convexe. Grâce à cette propriété, lorsqu'un modèle de régression linéaire converge, nous savons que le modèle a identifié les pondérations et le biais qui génèrent la perte la plus faible.
Si nous créons un graphique du graphe de fonction de perte d'un modèle comportant une seule caractéristique, nous pouvons voir sa forme convexe. Vous trouverez ci-dessous la surface de perte de l'ensemble de données sur les miles par gallon utilisé dans les exemples précédents. Le poids est sur l'axe X, le biais sur l'axe Y et la perte sur l'axe Z:
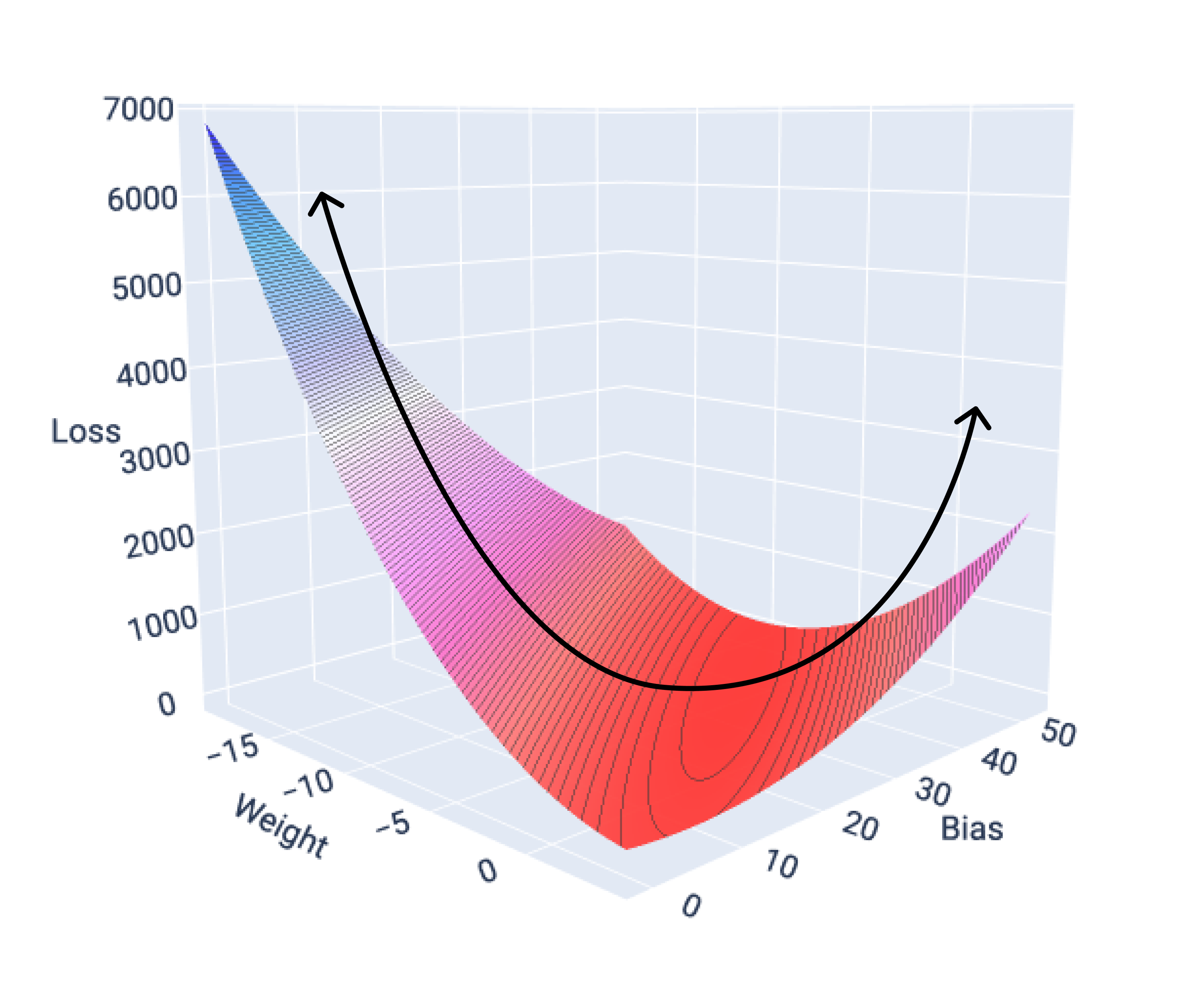
Figure 17. Surface de perte qui montre sa forme convexe.
Dans cet exemple, une pondération de -5,44 et un biais de 35,94 produisent la perte la plus faible à 5,54:
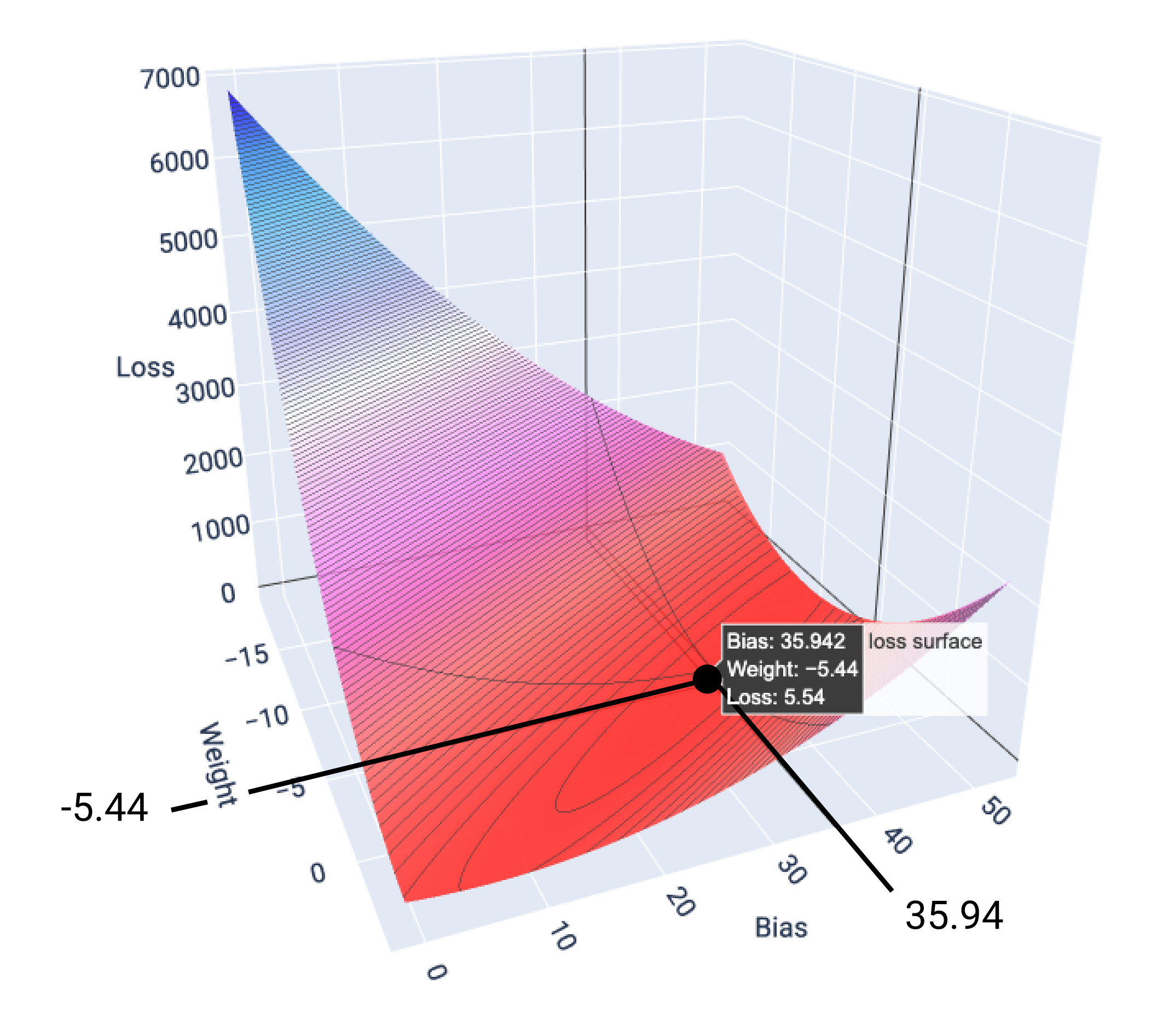
Figure 18 : Surface de perte montrant les valeurs de poids et de biais qui produisent la perte la plus faible.
Un modèle linéaire converge lorsqu'il a trouvé la perte minimale. Par conséquent, les itérations supplémentaires ne font que déplacer les valeurs de poids et de biais de très petites quantités autour du minimum. Si nous créions un graphique des pondérations et des points de biais pendant la descente de gradient, les points ressemblaient à une balle qui descendait une colline et s'arrêtaient au point où il n'y a plus de pente descendante.
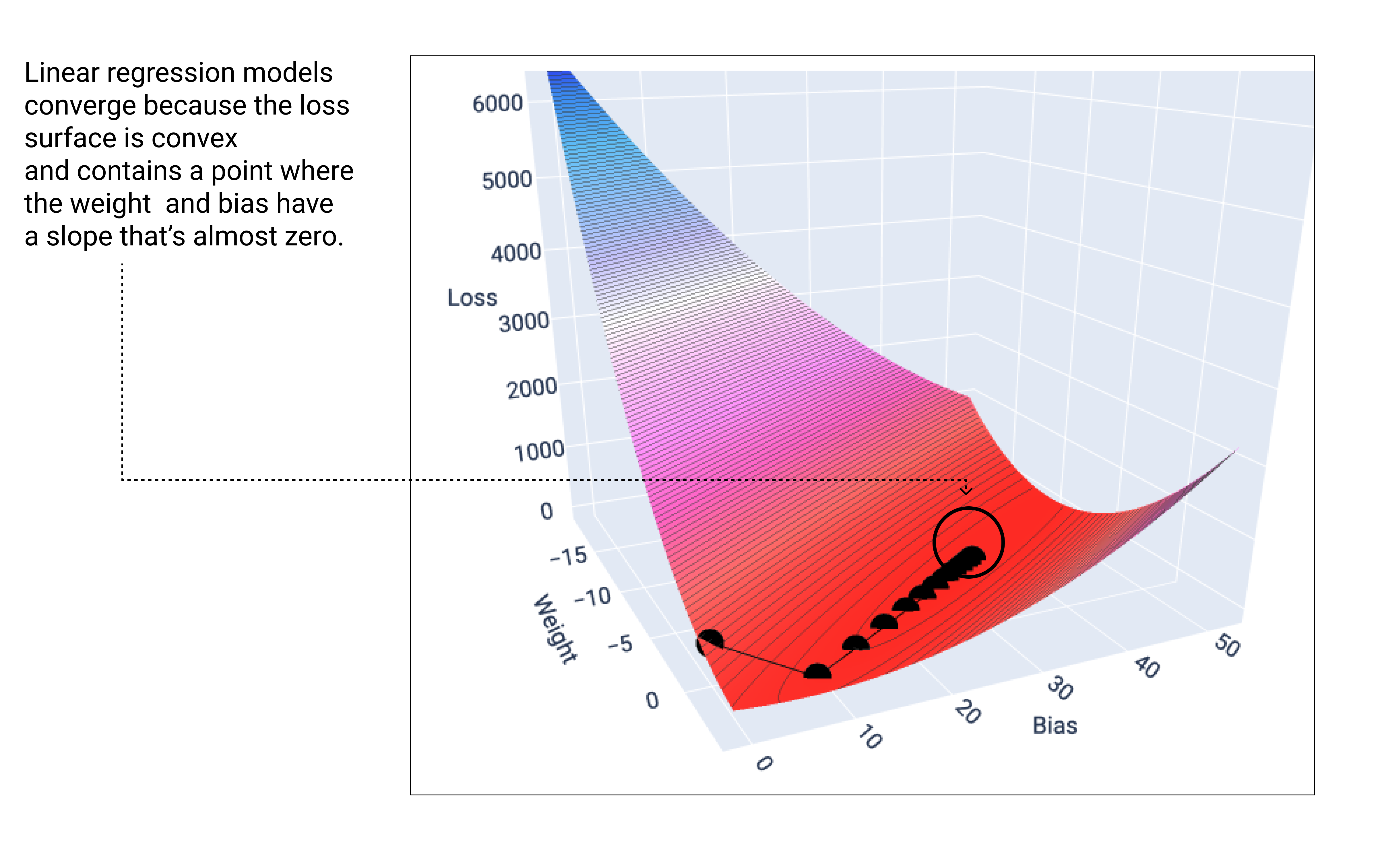
Figure 19 Graphique de perte affichant les points de descente de gradient s'arrêtant au point le plus bas du graphique
Notez que les points de perte noirs créent la forme exacte de la courbe de fonction de perte: une forte baisse avant de baisser progressivement jusqu'à ce qu'ils atteignent le point le plus bas du graphe de fonction de perte.
Il est important de noter que le modèle ne trouve presque jamais le minimum exact pour chaque pondération et biais, mais une valeur très proche. Il est également important de noter que le minimum des poids et du biais ne correspond pas à une perte nulle, mais uniquement à une valeur qui produit la perte la plus faible pour ce paramètre.
En utilisant les valeurs de poids et de biais qui produisent la perte la plus faible (dans ce cas, un poids de -5,44 et un biais de 35,94), nous pouvons représenter le modèle graphiquement pour voir dans quelle mesure il s'adapte aux données:
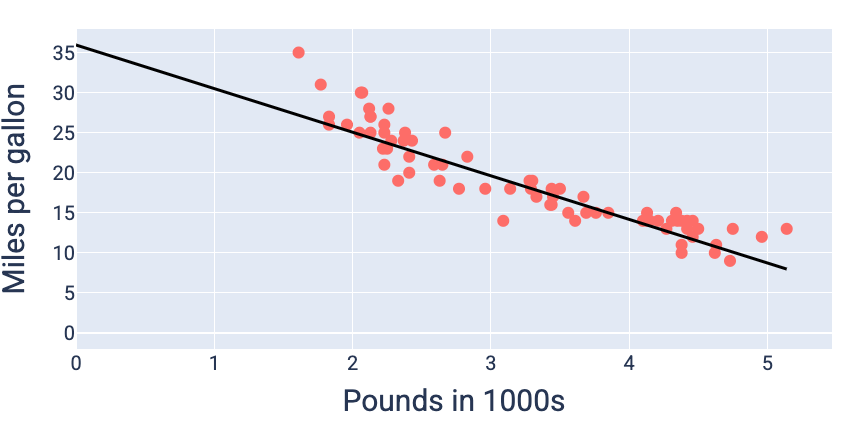
Figure 20. Modèle représenté graphiquement à l'aide des valeurs de pondération et de biais qui génèrent la perte la plus faible.
Il s'agit du meilleur modèle pour cet ensemble de données, car aucune autre valeur de poids et de biais ne produit un modèle avec une perte plus faible.