Doğrusal regresyon: Gradyan inişi

Gradyan inişi, kaybı en düşük olan modeli oluşturacak ağırlıkları ve önyargıyı yinelemeli olarak bulan matematiksel bir tekniktir. Gradyan inişi, kullanıcı tanımlı bir dizi yineleme için aşağıdaki işlemi tekrarlayarak en iyi ağırlığı ve yanlılığı bulur.

Model, sıfıra yakın rastgele ağırlıklar ve sapmalarla eğitime başlar, ardından aşağıdaki adımları tekrarlar:

1. Mevcut ağırlık ve önyargıyla kaybı hesaplayın.

2. Ağırlıkları ve kaybı azaltan önyargıyı hangi yönde hareket ettireceğinizi belirleyin.

3. Ağırlık ve önyargı değerlerini, kaybı azaltacak yönde küçük bir miktar hareket ettirin.

4. Birinci adıma dönün ve model kaybı daha fazla azaltamayacak duruma gelene kadar işlemi tekrarlayın.

Aşağıdaki şemada, en düşük kayıpla modeli üreten ağırlıkları ve yanlılığı bulmak için gradyan inişinin gerçekleştirdiği yinelemeli adımlar özetlenmektedir.

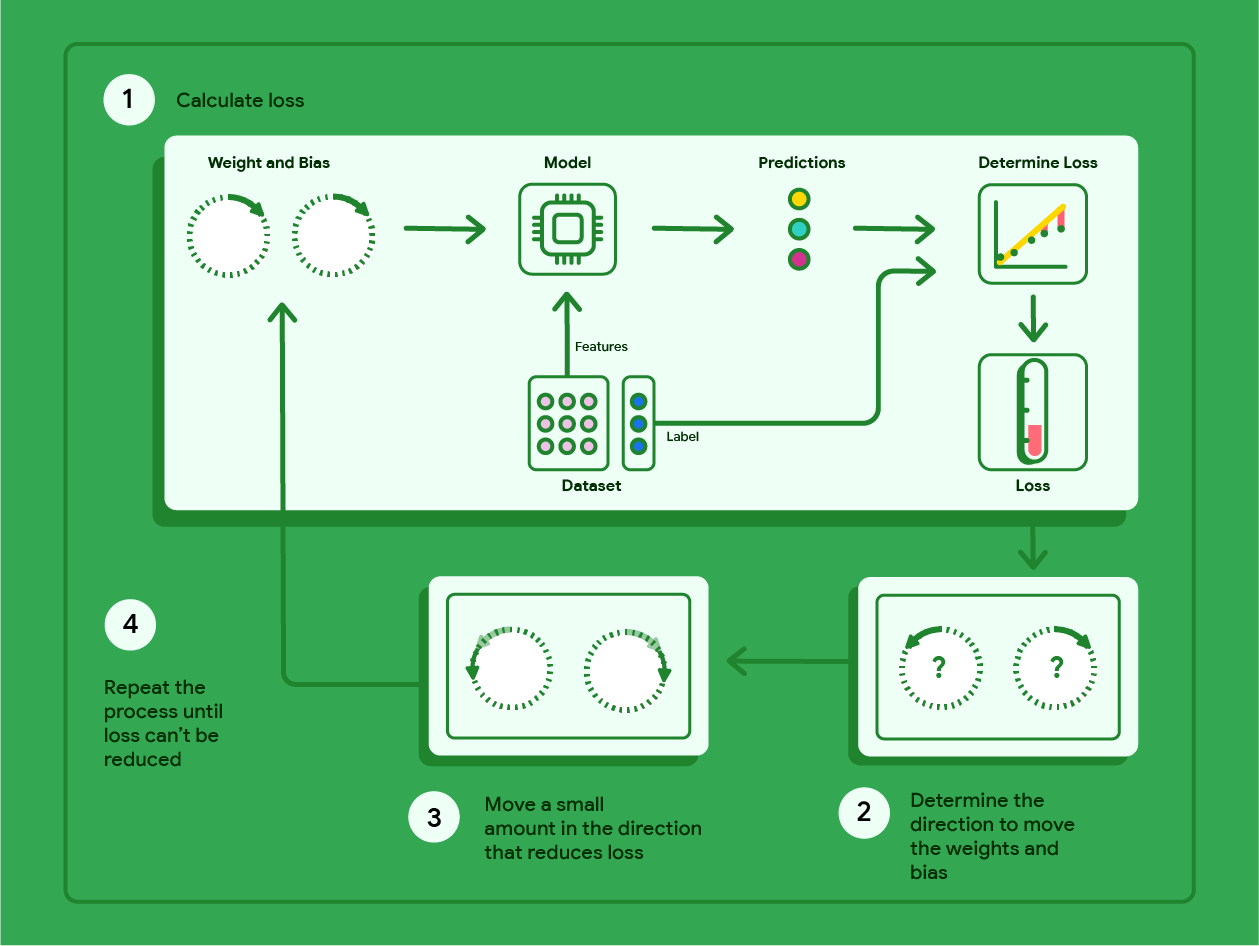
Şekil 11. Gradyan inişi, en düşük kayıpla modeli üreten ağırlıkları ve önyargıyı bulan yinelemeli bir süreçtir.

Gradyan inişinin arkasındaki matematik hakkında daha fazla bilgi edinmek için artı simgesini tıklayın.

Somut düzeyde, bir arabanın ağırlığı (libre cinsinden) ve galon başına mil derecesiyle ilgili yedi örnek içeren küçük bir veri kümesi kullanarak gradyan inişi adımlarını inceleyebiliriz:

Binlerce sterlin (özellik)	Mil/galon (etiket)
3,5	18
3,69	15
3,44	18
3,43	16
4,34	15
4,42	14
2,37	24

1. Model, ağırlığı ve önyargıyı sıfıra ayarlayarak eğitime başlar:
$$ \small{Weight:\ 0} $$ $$ \small{Bias:\ 0} $$ $$ \small{y = 0 + 0(x_1)} $$
2. Mevcut model parametreleriyle MSE kaybını hesaplayın:
$$ \small{Loss = \frac{(18-0)^2 + (15-0)^2 + (18-0)^2 + (16-0)^2 + (15-0)^2 + (14-0)^2 + (24-0)^2}{7}} $$ $$ \small{Loss= 303.71} $$
3. Her ağırlık ve önyargı noktasında kayıp fonksiyonuna teğet olan doğrunun eğimini hesaplayın:
$$ \small{Weight\ slope: -119.7} $$ $$ \small{Bias\ slope: -34.3} $$

Eğimi hesaplama hakkında bilgi edinmek için artı simgesini tıklayın.

Ağırlık ve önyargıya teğet olan çizgilerin eğimini elde etmek için kayıp fonksiyonunun ağırlık ve önyargıya göre türevini alırız ve ardından denklemleri çözeriz.

Tahmin yapma denklemini şu şekilde yazarız:
$ f_{w,b}(x) = (w*x)+b $.

Gerçek değeri $ y $ olarak yazarız.

MSE'yi hesaplamak için şu formülü kullanırız:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
Burada $i$, $i.$ eğitim örneğini, $M$ ise örnek sayısını ifade eder.

Ağırlık türevi

Ağırlığa göre kayıp fonksiyonunun türevi şu şekilde yazılır:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $


ve şu şekilde değerlendirilir:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $

Önce her tahmini değerden gerçek değeri çıkarıp sonucu özellik değerinin iki katıyla çarpıyoruz. Ardından, toplamı örnek sayısına böleriz. Sonuç, ağırlık değerine teğet olan doğrunun eğimidir.

Bu denklemi ağırlık ve yanlılık sıfıra eşit olacak şekilde çözersek doğrunun eğimi -119, 7 olur.

Eğilim türevi

Kaybın türevi, önyargıya göre şu şekilde yazılır:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $


ve şu şekilde değerlendirilir:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $

Öncelikle, her tahmini değerden gerçek değeri çıkarıp sonucu ikiyle çarpıyoruz. Ardından, toplamı örnek sayısına böleriz. Sonuç, eğrinin eğim değerine teğet olan doğrunun eğimidir.

Bu denklemi ağırlık ve yanlılık sıfıra eşit olacak şekilde çözersek doğrunun eğimi -34, 3 olur.

4. Bir sonraki ağırlığı ve önyargıyı elde etmek için negatif eğim yönünde küçük bir miktar hareket edin. Şimdilik "küçük tutar"ı rastgele 0, 01 olarak tanımlayacağız:
$$ \small{New\ weight = old\ weight - (small\ amount * weight\ slope)} $$ $$ \small{New\ bias = old\ bias - (small\ amount * bias\ slope)} $$ $$ \small{New\ weight = 0 - (0.01)*(-119.7)} $$ $$ \small{New\ bias = 0 - (0.01)*(-34.3)} $$ $$ \small{New\ weight = 1.2} $$ $$ \small{New\ bias = 0.34} $$

Kaybı ve tekrarı hesaplamak için yeni ağırlık ve önyargıyı kullanın. İşlemi altı yineleme boyunca tamamladığımızda aşağıdaki ağırlıkları, sapmaları ve kayıpları elde ederiz:

Yineleme	Ağırlık	Önyargı	Kayıp (MSE)
1	0	0	303,71
2	1,20	0,34	170,84
3	2,05	0,59	103,17
4	2,66	0,78	68,70
5	3,09	0,91	51,13
6	3,40	1,01	42,17

Her güncellenen ağırlık ve önyargı ile kaybın azaldığını görebilirsiniz. Bu örnekte, altı yinelemeden sonra durduk. Pratikte bir model, yakınsayana kadar eğitilir. Bir model yakınsadığında, ek yinelemeler kaybı daha fazla azaltmaz. Bunun nedeni, gradyan inişinin kaybı neredeyse en aza indiren ağırlıkları ve önyargıyı bulmuş olmasıdır.

Model, yakınsama noktasını geçtikten sonra eğitilmeye devam ederse model, parametreleri en düşük değerleri etrafında sürekli olarak güncellediği için kayıp küçük miktarlarda dalgalanmaya başlar. Bu durum, modelin gerçekten yakınsadığını doğrulamayı zorlaştırabilir. Modelin yakınlaştığını onaylamak için kayıp değeri sabitlenene kadar eğitime devam etmeniz gerekir.

Model yakınsama ve kayıp eğrileri

Bir modeli eğitirken modelin yakınlaşmış olup olmadığını belirlemek için genellikle kayıp eğrisine bakarsınız. Kayıp eğrisi, model eğitilirken kaybın nasıl değiştiğini gösterir. Tipik bir kayıp eğrisi aşağıdaki gibidir. Y ekseninde kayıp, x ekseninde ise yineleme sayısı gösterilir:

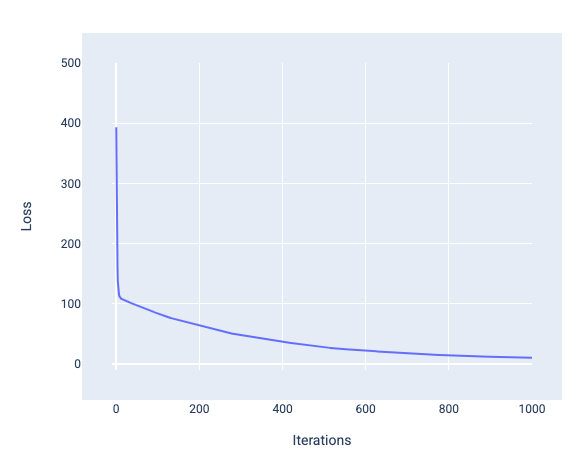
Şekil 12. Modelin 1.000. yineleme işaretinde yakınlaştığını gösteren kayıp eğrisi.

Kayıp değerinin ilk birkaç yinelemede önemli ölçüde azaldığını, ardından 1.000. yineleme civarında düzleşmeden önce kademeli olarak azaldığını görebilirsiniz. 1.000 yinelemeden sonra modelin yakınsadığından neredeyse emin olabiliriz.

Aşağıdaki şekillerde, modeli eğitim sürecinde üç noktada çiziyoruz: başlangıç, orta ve bitiş. Eğitim süreci sırasında modelin durumunu anlık görüntülerle görselleştirmek, ağırlıkların ve önyargının güncellenmesi, kaybın azaltılması ve model yakınsaması arasındaki bağlantıyı güçlendirir.

Şekillerde, modeli temsil etmek için belirli bir yinelemede türetilmiş ağırlıkları ve yanlılığı kullanırız. Veri noktaları ve model anlık görüntüsünün bulunduğu grafikte, modelden veri noktalarına giden mavi kayıp çizgileri kayıp miktarını gösterir. Çizgiler ne kadar uzun olursa kayıp da o kadar fazla olur.

Aşağıdaki şekilde, yaklaşık ikinci yinelemede modelin yüksek kayıp miktarı nedeniyle tahmin yapmada iyi olmadığı görülmektedir.

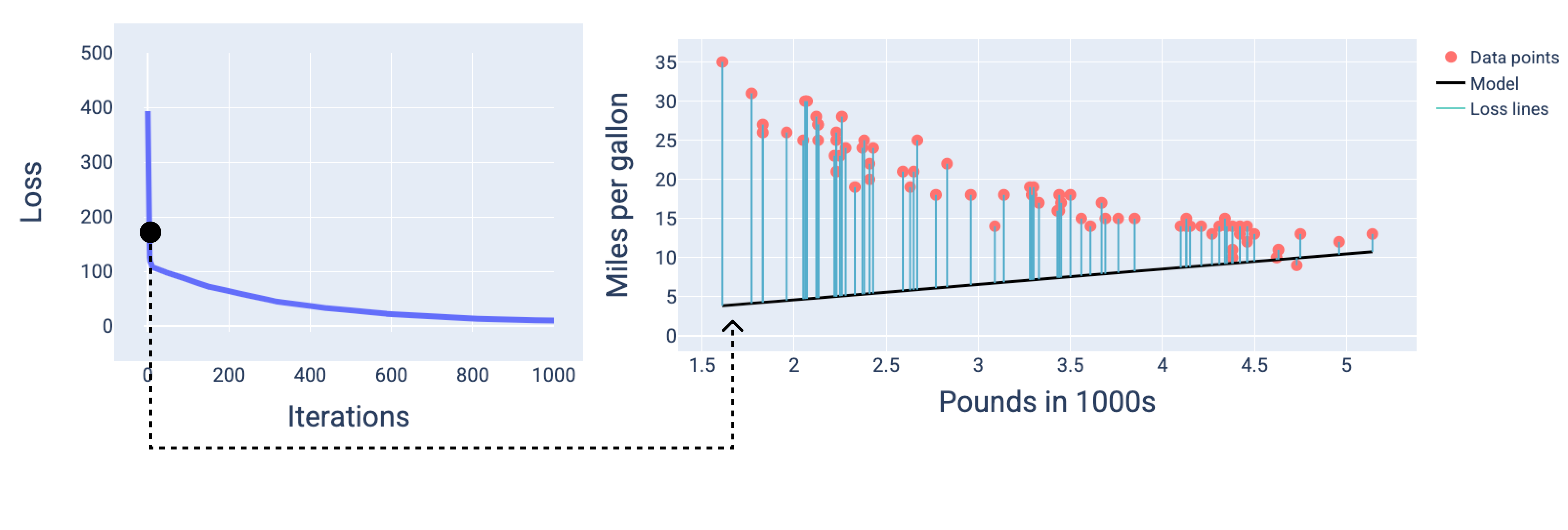
Şekil 13. Eğitim sürecinin başındaki modelin kayıp eğrisi ve anlık görüntüsü.

Yaklaşık 400. yinelemede, gradyan inişinin daha iyi bir model üreten ağırlığı ve önyargıyı bulduğunu görebiliriz.

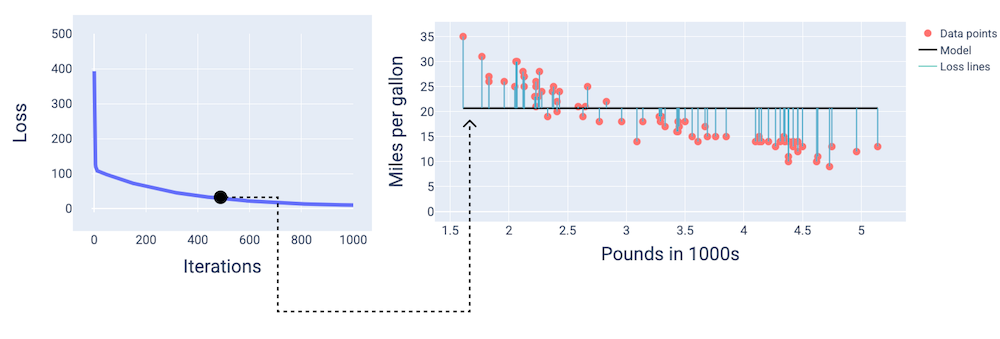
Şekil 14. Eğitimin yaklaşık ortasında modelin kaybı eğrisi ve anlık görüntüsü.

Yaklaşık 1.000 tekrardan sonra modelin yakınsadığını ve mümkün olan en düşük kayba sahip bir model oluşturduğunu görebiliriz.

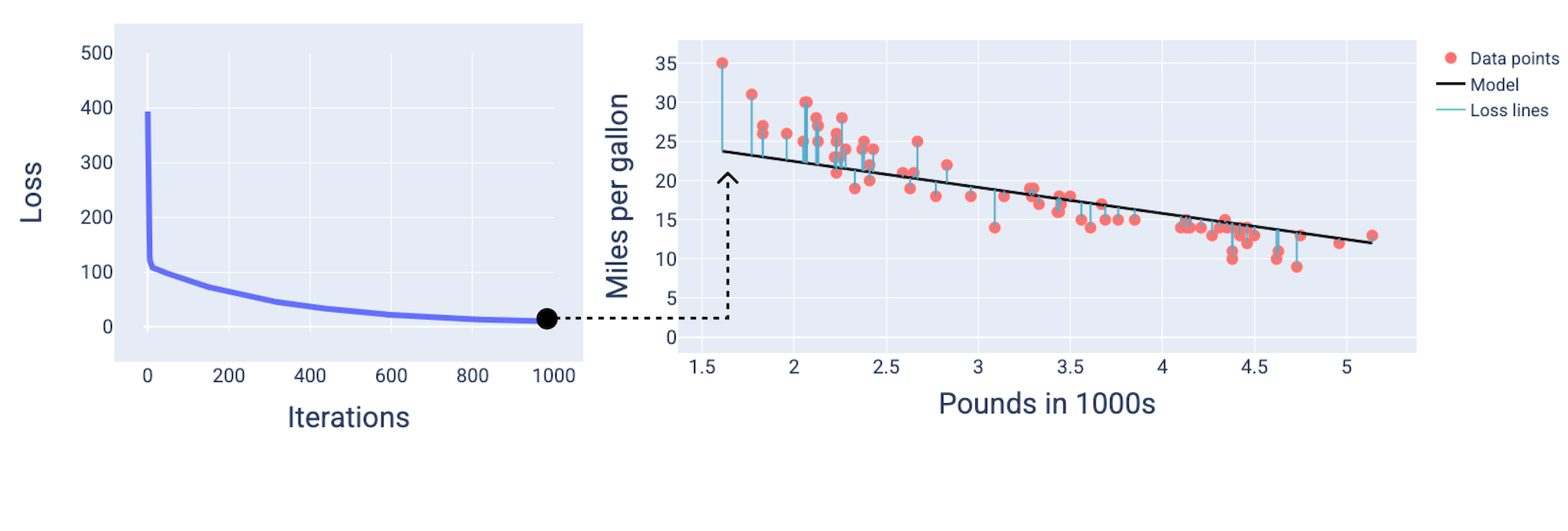
Şekil 15. Eğitim sürecinin sonuna doğru modelin kayıp eğrisi ve anlık görüntüsü.

Alıştırma: Anlayıp anlamadığınızı kontrol edin

Doğrusal regresyonda gradyan inişinin rolü nedir?

Gradyan inişi, kaybı en aza indiren en iyi ağırlıkları ve yanlılığı bulan yinelemeli bir süreçtir.

Gradyan inişi, bir modeli eğitirken ne tür bir kayıp kullanılacağını belirlemeye yardımcı olur (ör. L₁ veya L₂).

Model eğitimi için kayıp fonksiyonu seçilirken gradyan inişi kullanılmaz.

Gradyan inişi, modelin daha iyi tahminler yapmasına yardımcı olmak için aykırı değerleri veri kümesinden kaldırır.

Gradyan inişi, veri kümesini değiştirmez.

Yakınsama ve dışbükey fonksiyonlar

Doğrusal modellerin kayıp işlevleri her zaman dışbükey bir yüzey oluşturur. Bu özellik sayesinde, doğrusal regresyon modeli yakınsadığında modelin en düşük kaybı üreten ağırlıkları ve yanlılığı bulduğunu biliriz.

Tek bir özelliğe sahip bir modelin kayıp yüzeyini grafiğe dökersek dışbükey şeklini görebiliriz. Aşağıda, varsayıma dayalı bir galon başına mil veri kümesinin kayıp yüzeyi gösterilmektedir. Ağırlık x ekseninde, sapma y ekseninde ve kayıp z ekseninde gösterilir:

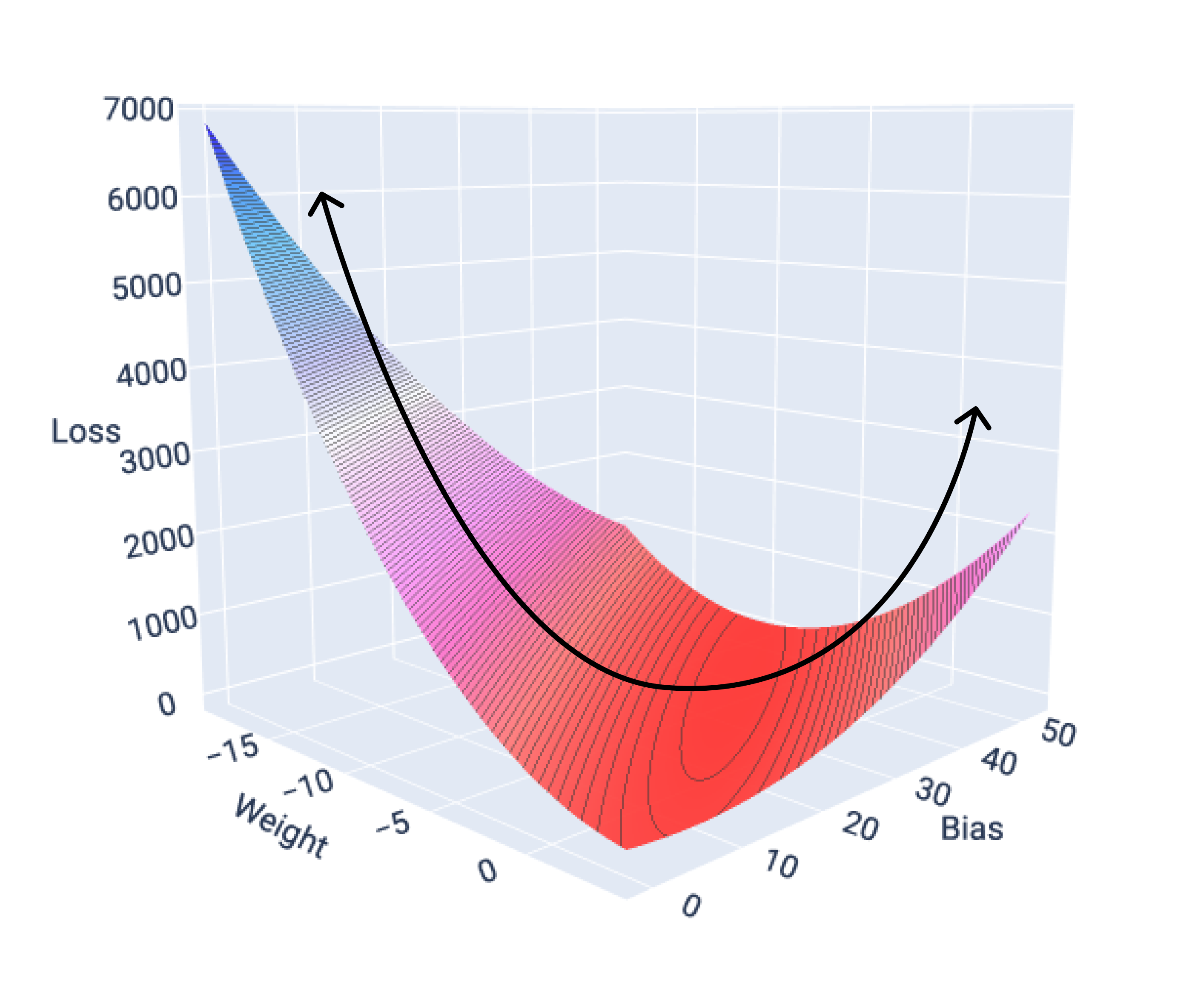
16.şekil Dışbükey şeklini gösteren kayıp yüzey.

Bu örnekte, -5,44 ağırlık ve 35,94 sapma ile 5,54'te en düşük kayıp elde edilir:

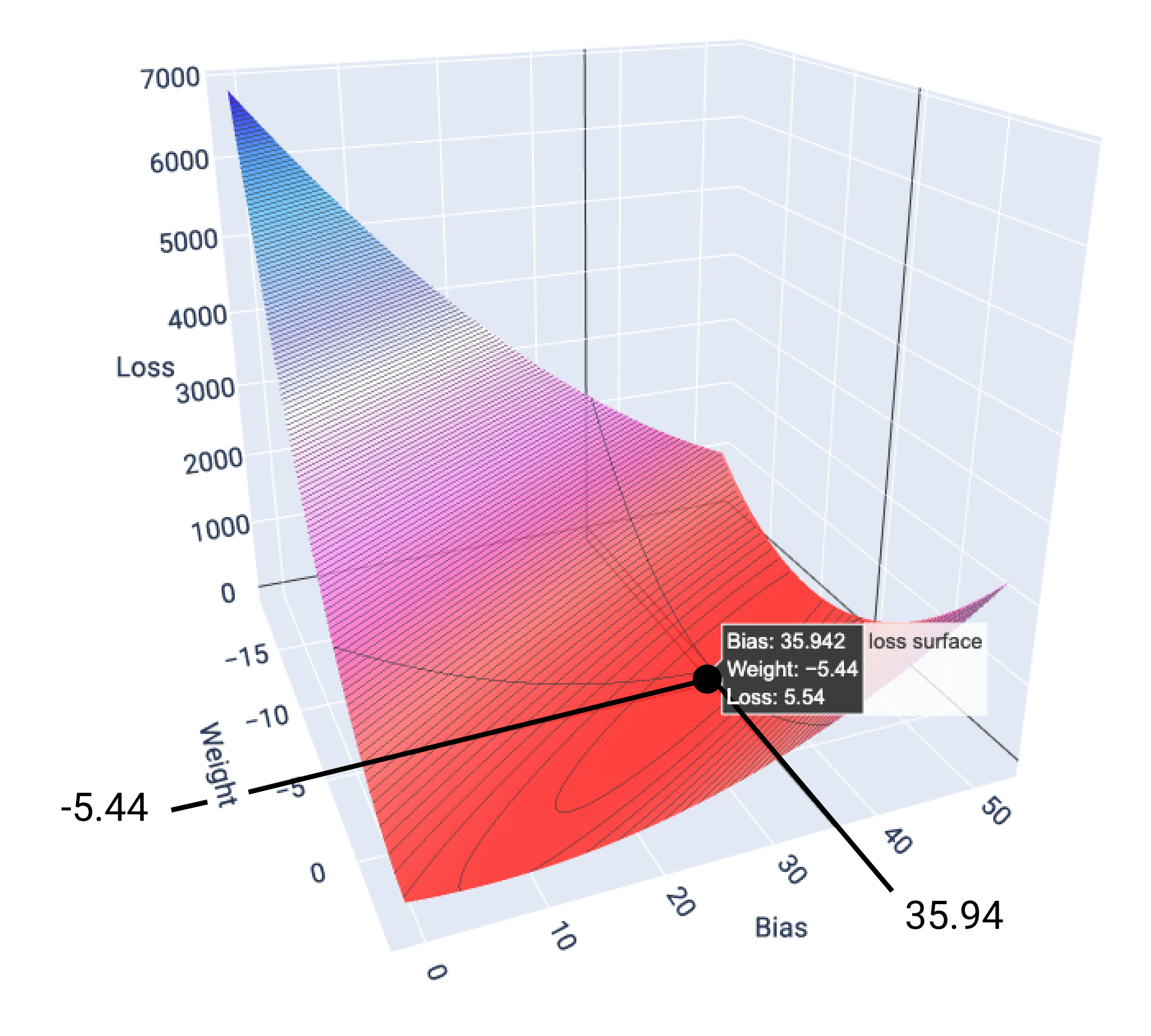
Şekil 17. En düşük kaybı üreten ağırlık ve önyargı değerlerini gösteren kayıp yüzeyi.

Doğrusal bir model, minimum kaybı bulduğunda yakınsar. Bu nedenle, ek yinelemeler yalnızca gradyan inişinin ağırlık ve önyargı değerlerini minimumun etrafında çok küçük miktarlarda hareket ettirmesine neden olur. Eğim inişi sırasında ağırlıkları ve sapma noktalarını grafiğe dökersek noktalar, bir tepeden aşağı yuvarlanan topa benzer ve sonunda aşağı doğru eğimin olmadığı noktada durur.

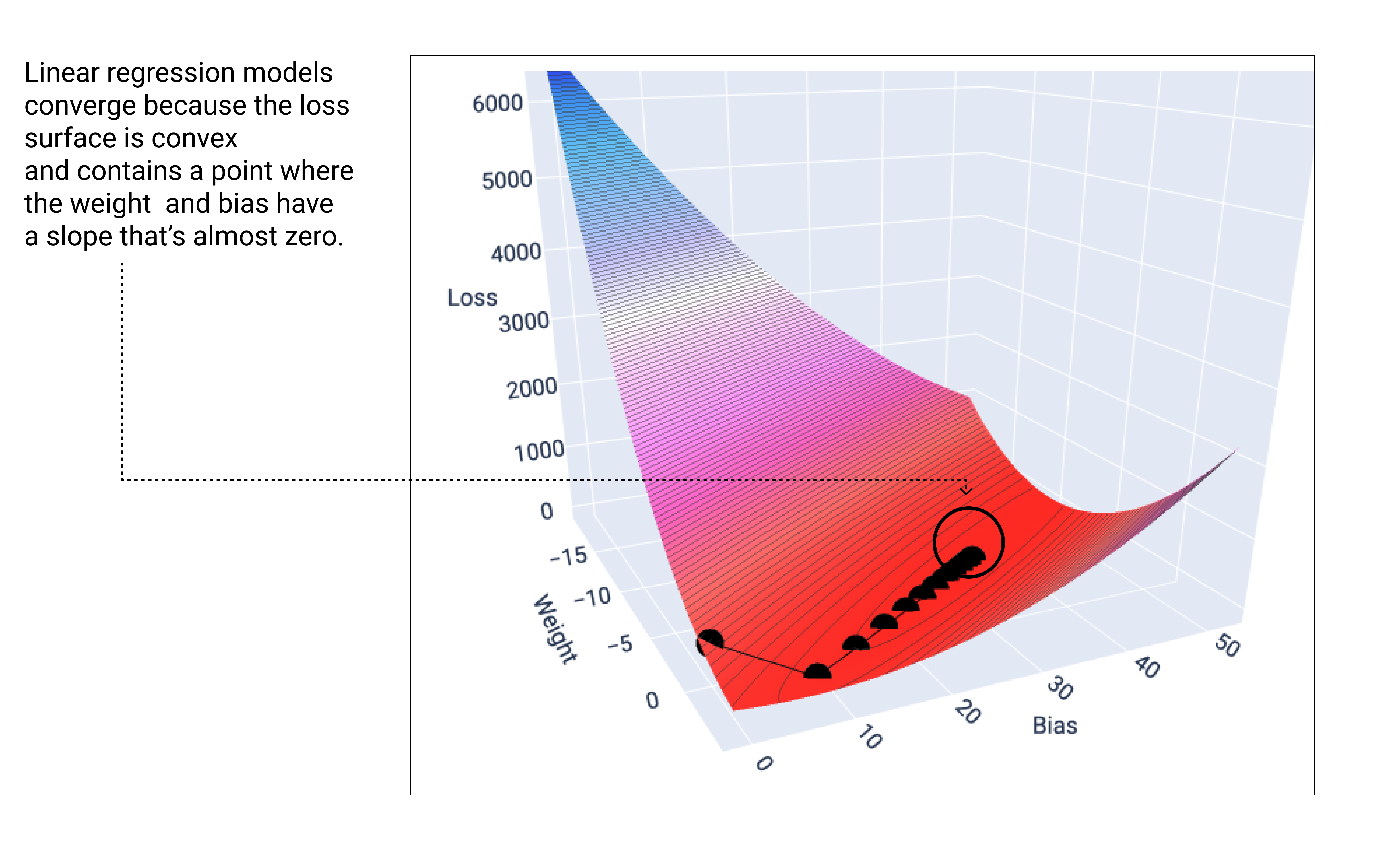
Şekil 18. Gradyan iniş noktalarının grafikteki en düşük noktada durduğunu gösteren kayıp grafiği.

Siyah kayıp noktalarının, kayıp eğrisinin tam şeklini oluşturduğuna dikkat edin: Kayıp yüzeyindeki en düşük noktaya ulaşana kadar kademeli olarak aşağı eğimlenmeden önce dik bir düşüş.

Modelin, her ağırlık ve önyargı için tam minimum değeri neredeyse hiç bulmadığını, bunun yerine bu değere çok yakın bir değer bulduğunu unutmamak önemlidir. Ağırlıklar ve sapma için minimum değerin sıfır kayba karşılık gelmediğini, yalnızca bu parametre için en düşük kaybı üreten bir değere karşılık geldiğini de unutmayın.

En düşük kaybı üreten ağırlık ve önyargı değerlerini (bu örnekte -5,44 ağırlık ve 35,94 önyargı) kullanarak modeli grafiğe dökebilir ve verilere ne kadar iyi uyduğunu görebiliriz:

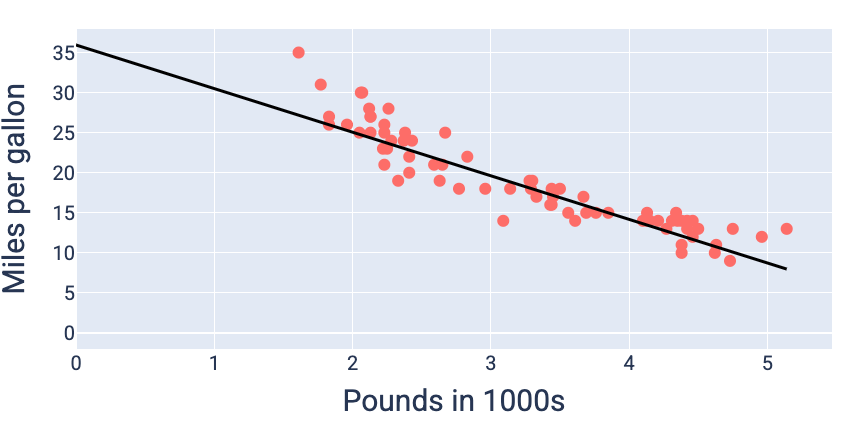
Şekil 19. En düşük kaybı üreten ağırlık ve önyargı değerleri kullanılarak oluşturulan model grafiği.

Başka hiçbir ağırlık ve önyargı değeri daha düşük kayıplı bir model üretmediği için bu veri kümesi için en iyi model budur.

Önemli terimler:

• Convergence
• Dışbükey işlev
• Gradyan inişi
• Yineleme (Iteration)
• Kayıp eğrisi