গ্রেডিয়েন্ট ডিসেন্ট হল একটি গাণিতিক কৌশল যা পুনরাবৃত্তভাবে ওজন এবং পক্ষপাত খুঁজে বের করে যা সর্বনিম্ন ক্ষতি সহ মডেল তৈরি করে। গ্রেডিয়েন্ট ডিসেন্ট ব্যবহারকারী-সংজ্ঞায়িত পুনরাবৃত্তির জন্য নিম্নলিখিত প্রক্রিয়াটি পুনরাবৃত্তি করে সর্বোত্তম ওজন এবং পক্ষপাত খুঁজে বের করে।
মডেলটি শূন্যের কাছাকাছি এলোমেলো ওজন এবং পক্ষপাত দিয়ে প্রশিক্ষণ শুরু করে এবং তারপর নিম্নলিখিত পদক্ষেপগুলি পুনরাবৃত্তি করে:
বর্তমান ওজন এবং পক্ষপাত দিয়ে ক্ষতি গণনা করুন।
ওজন এবং পক্ষপাত যা ক্ষতি কমায় তা সরানোর দিক নির্ধারণ করুন।
ওজন এবং পক্ষপাতের মানগুলিকে এমন দিকে অল্প পরিমাণে সরান যা ক্ষতি হ্রাস করে।
প্রথম ধাপে ফিরে যান এবং প্রক্রিয়াটি পুনরাবৃত্তি করুন যতক্ষণ না মডেলটি ক্ষতি আরও কমাতে পারে।
নিচের চিত্রটিতে গ্রেডিয়েন্ট ডিসেন্টের পুনরাবৃত্ত পদক্ষেপগুলি দেখানো হয়েছে যা ওজন এবং পক্ষপাত খুঁজে বের করার জন্য সর্বনিম্ন ক্ষতি সহ মডেল তৈরি করে।
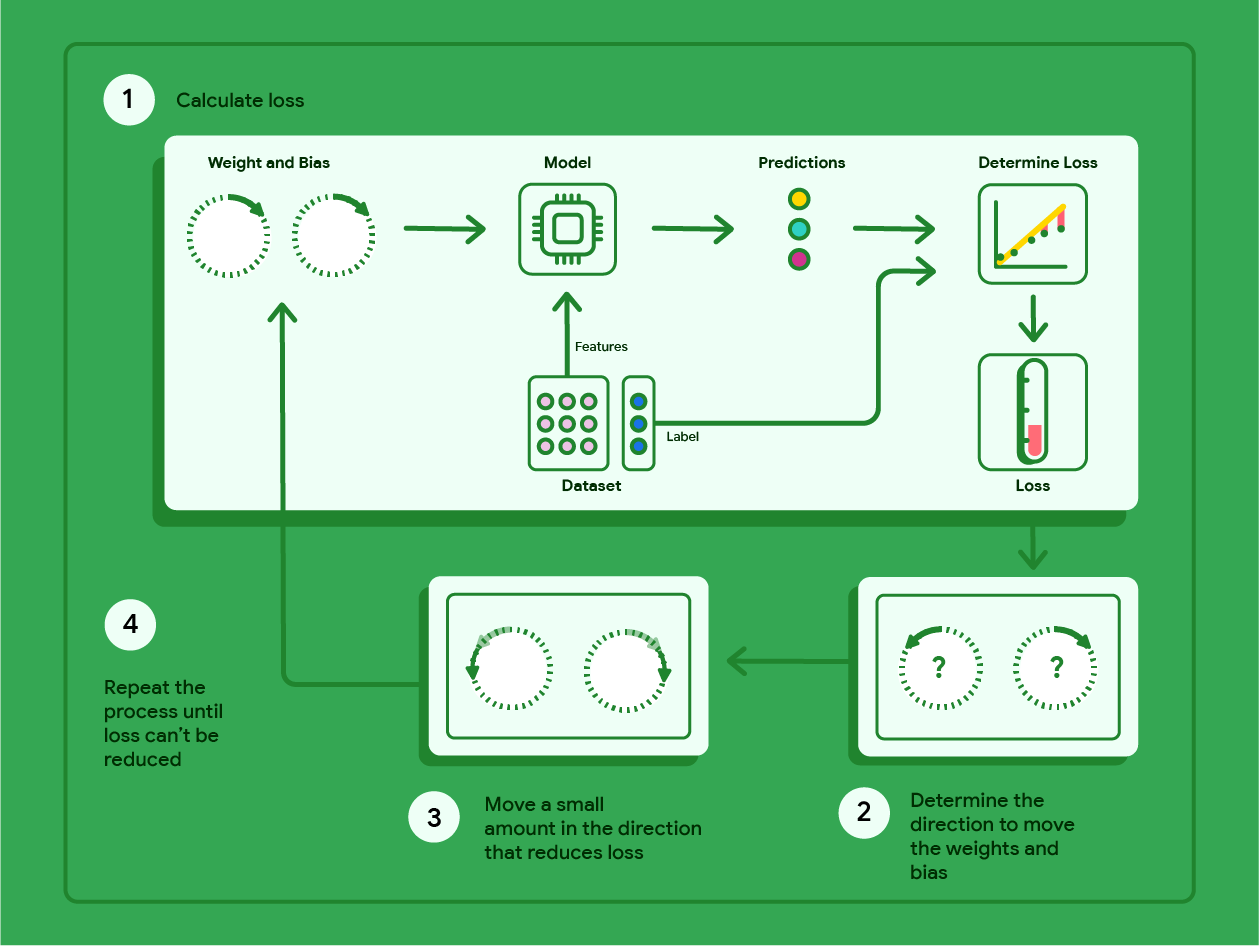
চিত্র ১১. গ্রেডিয়েন্ট ডিসেন্ট হল একটি পুনরাবৃত্ত প্রক্রিয়া যা ওজন এবং পক্ষপাত খুঁজে বের করে যা সর্বনিম্ন ক্ষতি সহ মডেল তৈরি করে।
গ্রেডিয়েন্ট ডিসেন্টের পিছনের গণিত সম্পর্কে আরও জানতে প্লাস আইকনে ক্লিক করুন।
একটি নির্দিষ্ট স্তরে, আমরা সাতটি উদাহরণ সহ নিম্নলিখিত ছোট জ্বালানী-দক্ষতা ডেটাসেট এবং ক্ষতির মেট্রিক হিসাবে গড় স্কোয়ারড ত্রুটি (MSE) ব্যবহার করে গ্রেডিয়েন্ট ডিসেন্ট ধাপগুলি অতিক্রম করতে পারি:
| ১০০০ সেকেন্ডে পাউন্ড (বৈশিষ্ট্য) | মাইল প্রতি গ্যালন (লেবেল) |
|---|---|
| ৩.৫ | ১৮ |
| ৩.৬৯ | ১৫ |
| ৩.৪৪ | ১৮ |
| ৩.৪৩ | ১৬ |
| ৪.৩৪ | ১৫ |
| ৪.৪২ | ১৪ |
| ২.৩৭ | ২৪ |
- মডেলটি ওজন এবং পক্ষপাত শূন্যে সেট করে প্রশিক্ষণ শুরু করে:
- বর্তমান মডেল প্যারামিটার দিয়ে MSE ক্ষতি গণনা করুন:
- প্রতিটি ওজন এবং পক্ষপাতের উপর ক্ষতি ফাংশনের স্পর্শকের ঢাল গণনা করুন:
- পরবর্তী ওজন এবং পক্ষপাত পেতে ঋণাত্মক ঢালের দিকে অল্প পরিমাণ সরান। আপাতত, আমরা ইচ্ছাকৃতভাবে "ছোট পরিমাণ" কে 0.01 হিসাবে সংজ্ঞায়িত করব:
ঢাল গণনা সম্পর্কে জানতে প্লাস আইকনে ক্লিক করুন।
ওজন এবং পক্ষপাতের সাথে স্পর্শক রেখাগুলির ঢাল পেতে, আমরা ওজন এবং পক্ষপাতের সাপেক্ষে ক্ষতি ফাংশনের ডেরিভেটিভ নিই এবং তারপর সমীকরণগুলি সমাধান করি।
আমরা ভবিষ্যদ্বাণী করার সমীকরণটি এভাবে লিখব:
$ f_{w,b}(x) = (w*x)+b $.
আমরা প্রকৃত মানটি লিখব: $ y $।
আমরা MSE গণনা করব এইভাবে:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
যেখানে $i$ $ith$ প্রশিক্ষণের উদাহরণ উপস্থাপন করে এবং $M$ উদাহরণের সংখ্যা উপস্থাপন করে।
ওজনের সাপেক্ষে ক্ষতি ফাংশনের ডেরিভেটিভটি এভাবে লেখা হয়েছে:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
এবং মূল্যায়ন করে:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
প্রথমে আমরা প্রতিটি পূর্বাভাসিত মানের যোগফল প্রকৃত মানের বিয়োগ করি এবং তারপর বৈশিষ্ট্য মানের দ্বিগুণ দিয়ে গুণ করি। তারপর আমরা যোগফলকে উদাহরণের সংখ্যা দিয়ে ভাগ করি। ফলাফল হল ওজনের মানের সাথে রেখার ট্যানজেন্টের ঢাল।
যদি আমরা শূন্যের সমান ওজন এবং পক্ষপাত দিয়ে এই সমীকরণটি সমাধান করি, তাহলে আমরা রেখার ঢালের জন্য -119.7 পাব।
পক্ষপাত ডেরিভেটিভ পক্ষপাতের সাপেক্ষে ক্ষতি ফাংশনের ডেরিভেটিভটি এভাবে লেখা হয়েছে:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
এবং মূল্যায়ন করে:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
প্রথমে আমরা প্রতিটি পূর্বাভাসিত মানের যোগফল প্রকৃত মান বিয়োগ করে দুই দিয়ে গুণ করব। তারপর যোগফলকে উদাহরণের সংখ্যা দিয়ে ভাগ করব। ফলাফল হল রেখার ট্যানজেন্টের ঢাল এবং পক্ষপাতের মানের মধ্যে।
যদি আমরা শূন্যের সমান ওজন এবং পক্ষপাত দিয়ে এই সমীকরণটি সমাধান করি, তাহলে আমরা রেখার ঢালের জন্য -34.3 পাব।
নতুন ওজন এবং পক্ষপাত ব্যবহার করে ক্ষতি গণনা করুন এবং পুনরাবৃত্তি করুন। ছয়টি পুনরাবৃত্তির জন্য প্রক্রিয়াটি সম্পন্ন করলে, আমরা নিম্নলিখিত ওজন, পক্ষপাত এবং ক্ষতি পাব:
| পুনরাবৃত্তি | ওজন | পক্ষপাত | ক্ষতি (এমএসই) |
|---|---|---|---|
| ১ | 0 | 0 | ৩০৩.৭১ |
| ২ | ১.২০ | ০.৩৪ | ১৭০.৮৪ |
| ৩ | ২.০৫ | ০.৫৯ | ১০৩.১৭ |
| ৪ | ২.৬৬ | ০.৭৮ | ৬৮.৭০ |
| ৫ | ৩.০৯ | ০.৯১ | ৫১.১৩ |
| ৬ | ৩.৪০ | ১.০১ | ৪২.১৭ |
আপনি দেখতে পাচ্ছেন যে প্রতিটি আপডেট করা ওজন এবং পক্ষপাতের সাথে ক্ষতি কম হয়। এই উদাহরণে, আমরা ছয়টি পুনরাবৃত্তির পরে থামলাম। বাস্তবে, একটি মডেল একত্রিত না হওয়া পর্যন্ত প্রশিক্ষণ দেয়। যখন একটি মডেল একত্রিত হয়, তখন অতিরিক্ত পুনরাবৃত্তি ক্ষতি বেশি হ্রাস করে না কারণ গ্রেডিয়েন্ট ডিসেন্ট ওজন এবং পক্ষপাত খুঁজে পেয়েছে যা ক্ষতি প্রায় কমিয়ে দেয়।
যদি মডেলটি অতীতের অভিসৃতিকে প্রশিক্ষণ দিতে থাকে, তাহলে ক্ষতি অল্প পরিমাণে ওঠানামা করতে শুরু করে কারণ মডেলটি তাদের সর্বনিম্ন মানের চারপাশে পরামিতিগুলি ক্রমাগত আপডেট করে। এর ফলে মডেলটি আসলেই অভিসৃতি পেয়েছে কিনা তা যাচাই করা কঠিন হয়ে পড়তে পারে। মডেলটি অভিসৃতি হয়েছে কিনা তা নিশ্চিত করার জন্য, ক্ষতি স্থিতিশীল না হওয়া পর্যন্ত আপনাকে প্রশিক্ষণ চালিয়ে যেতে হবে।
মডেল কনভারজেন্স এবং লস কার্ভ
একটি মডেলকে প্রশিক্ষণ দেওয়ার সময়, আপনি প্রায়শই একটি ক্ষতির বক্ররেখা দেখেন যে মডেলটি একত্রিত হয়েছে কিনা। ক্ষতির বক্ররেখা দেখায় যে মডেলটি প্রশিক্ষণের সাথে সাথে ক্ষতি কীভাবে পরিবর্তিত হয়। একটি সাধারণ ক্ষতির বক্ররেখা নীচে দেখানো হল। ক্ষতি y-অক্ষে এবং পুনরাবৃত্তিগুলি x-অক্ষে থাকে:
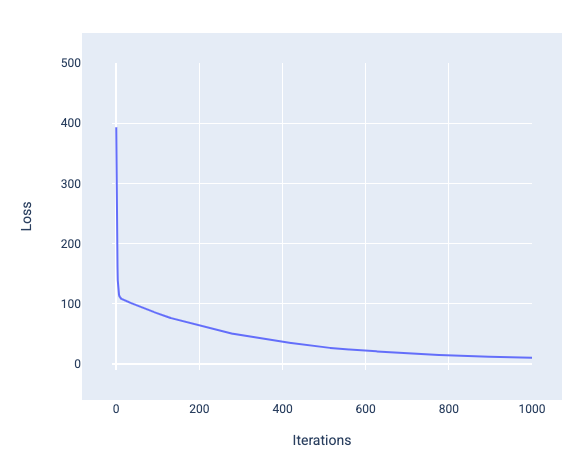
চিত্র ১২। ক্ষতির বক্ররেখা দেখায় যে মডেলটি ১০০০তম-পুনরাবৃত্তি চিহ্নের চারপাশে একত্রিত হচ্ছে।
আপনি দেখতে পাচ্ছেন যে প্রথম কয়েকটি পুনরাবৃত্তির সময় ক্ষতি নাটকীয়ভাবে হ্রাস পায়, তারপর ধীরে ধীরে হ্রাস পায় এবং ১,০০০ তম পুনরাবৃত্তির চিহ্নের কাছাকাছি চলে আসে। ১,০০০ পুনরাবৃত্তির পরে, আমরা বেশিরভাগ ক্ষেত্রে নিশ্চিত হতে পারি যে মডেলটি একত্রিত হয়েছে।
নিম্নলিখিত চিত্রগুলিতে, আমরা প্রশিক্ষণ প্রক্রিয়ার সময় তিনটি বিন্দুতে মডেলটি আঁকছি: শুরু, মাঝামাঝি এবং শেষ। প্রশিক্ষণ প্রক্রিয়ার সময় স্ন্যাপশটে মডেলের অবস্থা কল্পনা করা ওজন এবং পক্ষপাত আপডেট করা, ক্ষতি হ্রাস করা এবং মডেল অভিসৃতির মধ্যে যোগসূত্রকে দৃঢ় করে।
চিত্রগুলিতে, আমরা মডেলটি উপস্থাপন করার জন্য একটি নির্দিষ্ট পুনরাবৃত্তিতে প্রাপ্ত ওজন এবং পক্ষপাত ব্যবহার করি। ডেটা পয়েন্ট এবং মডেল স্ন্যাপশট সহ গ্রাফে, মডেল থেকে ডেটা পয়েন্ট পর্যন্ত নীল ক্ষতির রেখাগুলি ক্ষতির পরিমাণ দেখায়। রেখাগুলি যত দীর্ঘ হবে, ক্ষতি তত বেশি হবে।
নিচের চিত্রে, আমরা দেখতে পাচ্ছি যে দ্বিতীয় পুনরাবৃত্তির কাছাকাছি সময়ে মডেলটি ভবিষ্যদ্বাণী করতে ভালো হবে না কারণ ক্ষতির পরিমাণ বেশি।
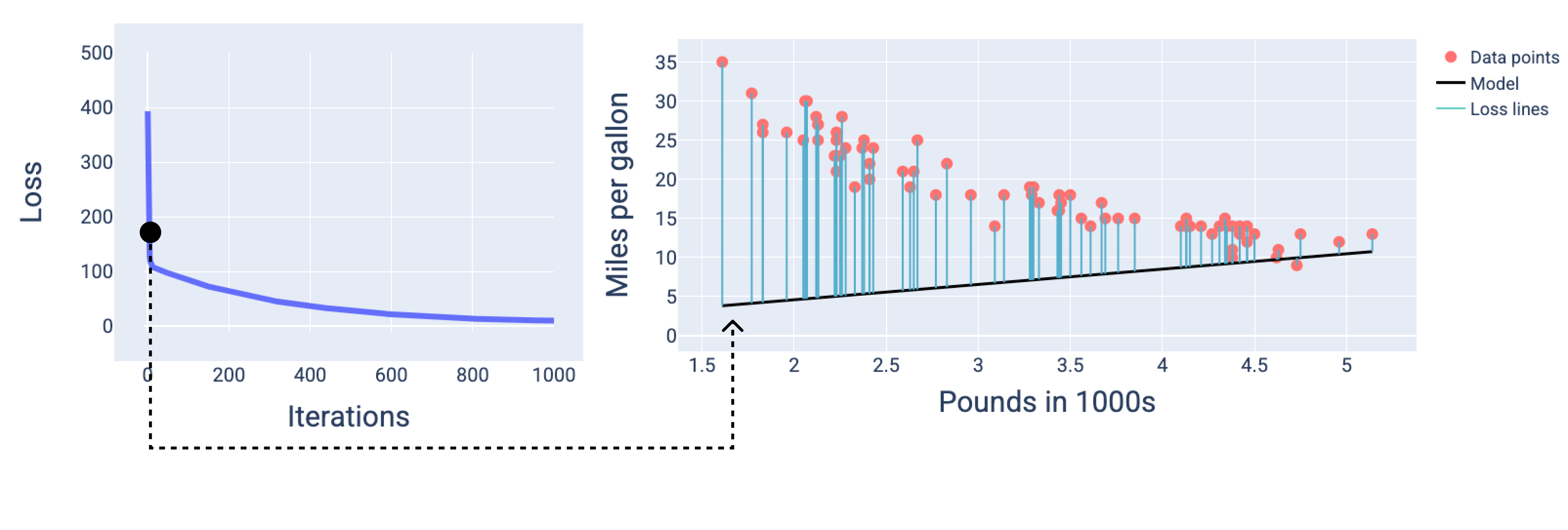
চিত্র ১৩। প্রশিক্ষণ প্রক্রিয়ার শুরুতে মডেলের ক্ষতির বক্ররেখা এবং স্ন্যাপশট।
প্রায় ৪০০ তম পুনরাবৃত্তিতে, আমরা দেখতে পাচ্ছি যে গ্রেডিয়েন্ট ডিসেন্ট এমন ওজন এবং পক্ষপাত খুঁজে পেয়েছে যা একটি ভাল মডেল তৈরি করে।
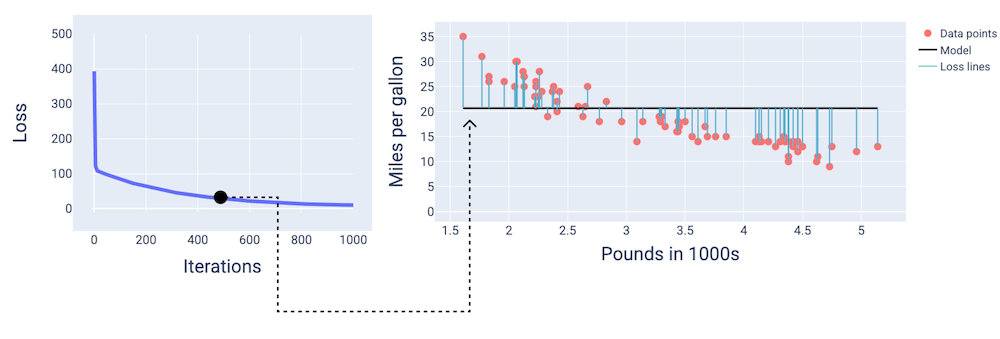
চিত্র ১৪। প্রশিক্ষণের মাঝামাঝি সময়ে মডেলের ক্ষতির বক্ররেখা এবং স্ন্যাপশট।
এবং প্রায় ১০০০তম পুনরাবৃত্তিতে, আমরা দেখতে পাচ্ছি যে মডেলটি একত্রিত হয়েছে, সর্বনিম্ন সম্ভাব্য ক্ষতি সহ একটি মডেল তৈরি করেছে।
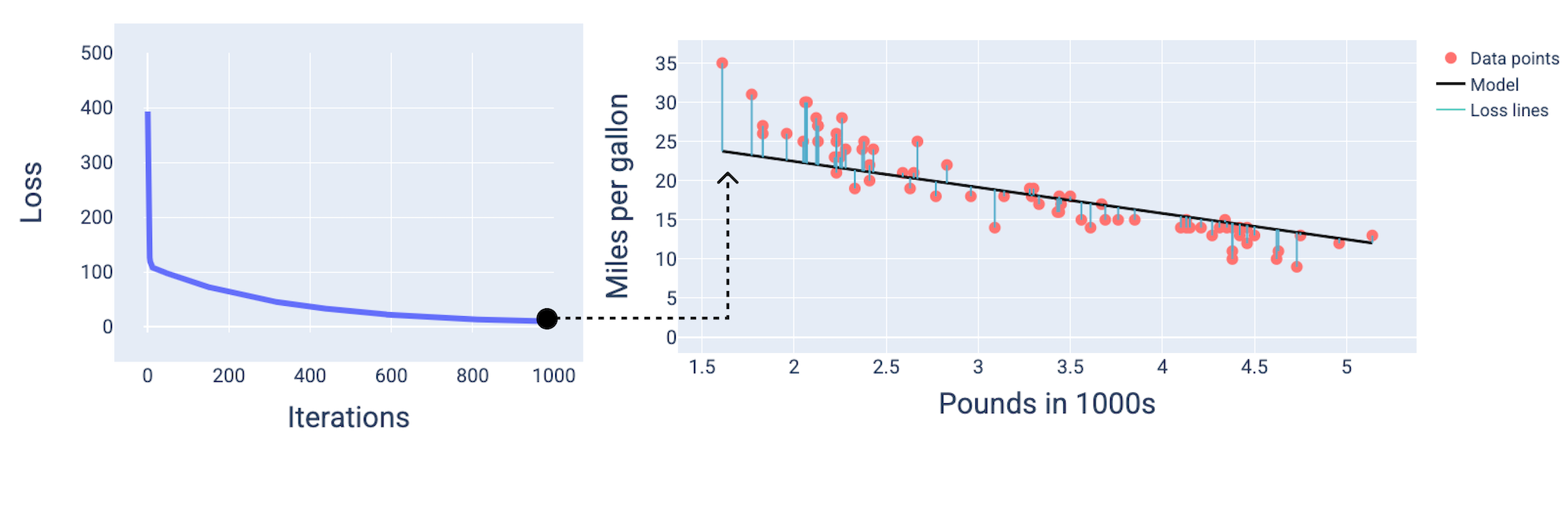
চিত্র ১৫। প্রশিক্ষণ প্রক্রিয়ার শেষের দিকে মডেলের ক্ষতির বক্ররেখা এবং স্ন্যাপশট।
অনুশীলন: আপনার বোধগম্যতা পরীক্ষা করুন
অভিসরণ এবং উত্তল ফাংশন
রৈখিক মডেলের জন্য ক্ষতি ফাংশন সর্বদা একটি উত্তল পৃষ্ঠ তৈরি করে। এই বৈশিষ্ট্যের ফলস্বরূপ, যখন একটি রৈখিক রিগ্রেশন মডেল একত্রিত হয়, তখন আমরা জানি যে মডেলটি সর্বনিম্ন ক্ষতির জন্য ওজন এবং পক্ষপাত খুঁজে পেয়েছে।
যদি আমরা একটি বৈশিষ্ট্যযুক্ত মডেলের জন্য ক্ষতি পৃষ্ঠের গ্রাফ আঁকি, তাহলে আমরা এর উত্তল আকৃতি দেখতে পাব। প্রতি গ্যালন ডেটাসেটে একটি কাল্পনিক মাইলের ক্ষতি পৃষ্ঠটি নিম্নরূপ। ওজন x-অক্ষে, পক্ষপাত y-অক্ষে এবং ক্ষতি z-অক্ষে:
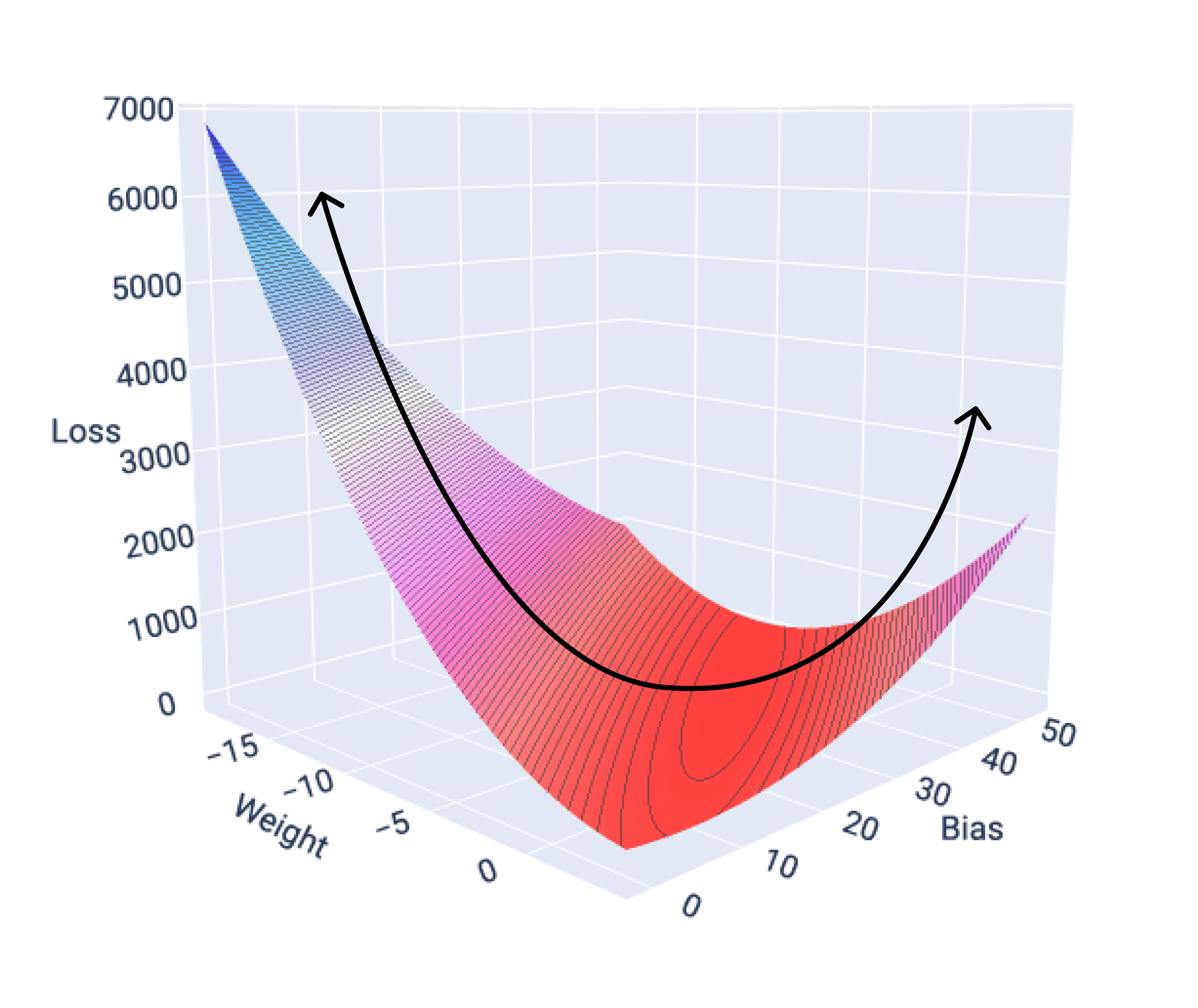
চিত্র ১৬। ক্ষয় পৃষ্ঠ যা তার উত্তল আকৃতি দেখায়।
এই উদাহরণে, -৫.৪৪ ওজন এবং ৩৫.৯৪ বায়াস সর্বনিম্ন ৫.৫৪ ক্ষতির কারণ হয়:
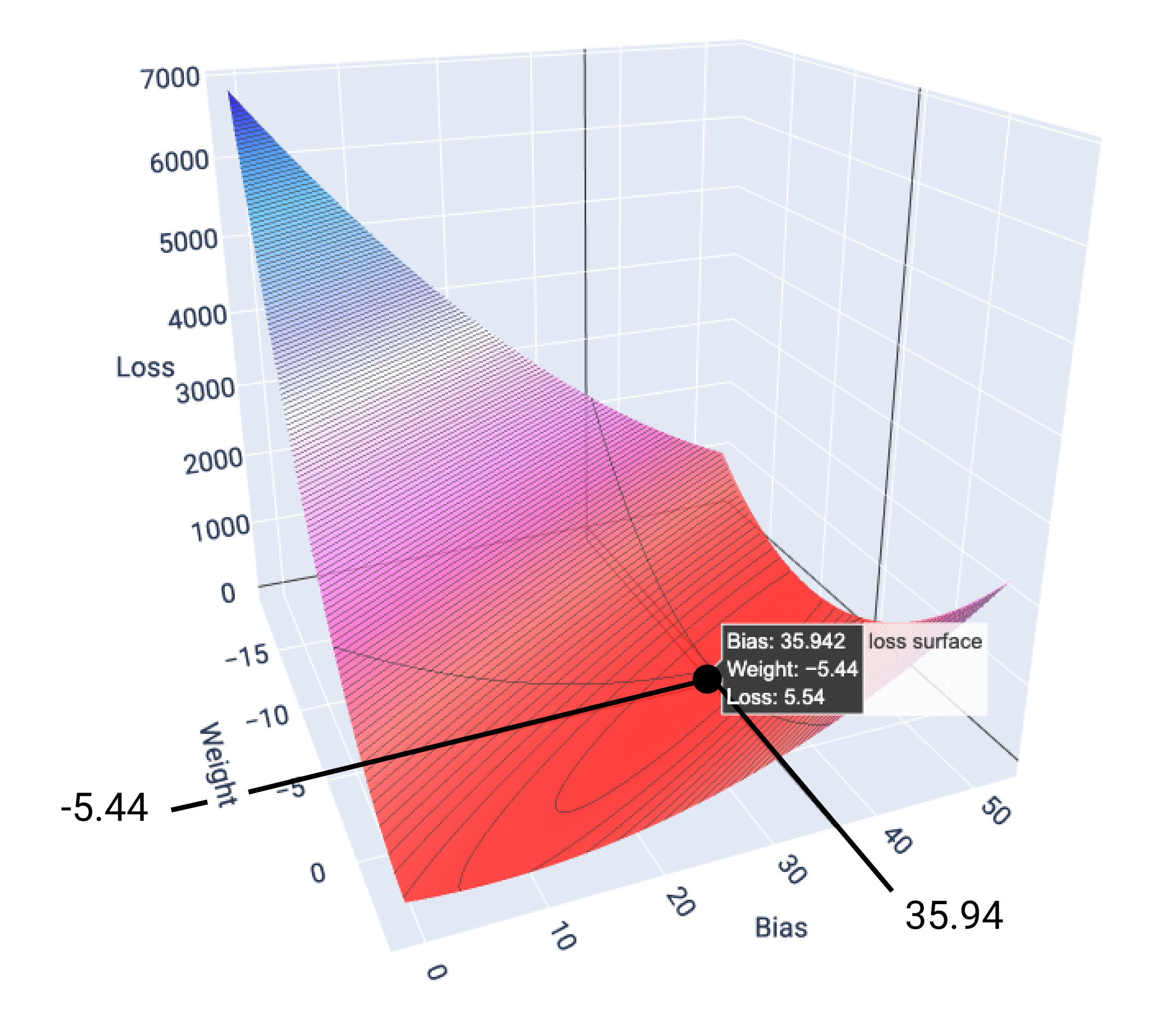
চিত্র ১৭। সর্বনিম্ন ক্ষতির কারণ হিসেবে ওজন এবং পক্ষপাতের মান দেখানো ক্ষতির পৃষ্ঠ।
একটি রৈখিক মডেল তখনই একত্রিত হয় যখন এটি সর্বনিম্ন ক্ষতি খুঁজে পায়। অতএব, অতিরিক্ত পুনরাবৃত্তির ফলে গ্রেডিয়েন্ট ডিসেন্টের ফলে ওজন এবং বায়াস মানগুলি খুব কম পরিমাণে সর্বনিম্নের চারপাশে সরে যায়। যদি আমরা গ্রেডিয়েন্ট ডিসেন্টের সময় ওজন এবং বায়াস পয়েন্টগুলি গ্রাফ করি, তাহলে পয়েন্টগুলি পাহাড়ের নিচে গড়িয়ে পড়া বলের মতো দেখাবে, অবশেষে এমন একটি বিন্দুতে থামবে যেখানে আর কোন নিম্নমুখী ঢাল নেই।
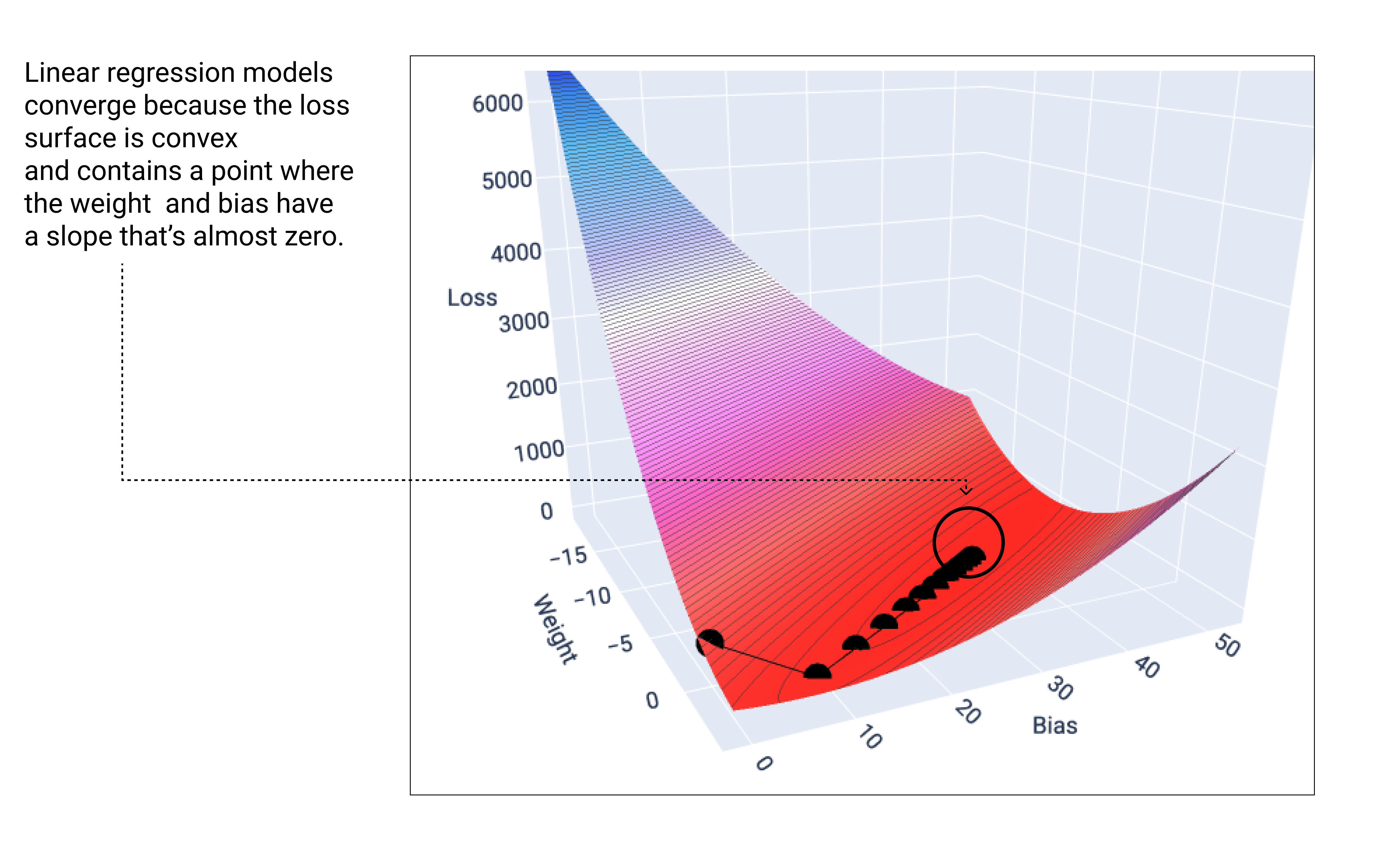
চিত্র ১৮। লোস গ্রাফে গ্রাফের সর্বনিম্ন বিন্দুতে থেমে থাকা গ্রেডিয়েন্ট ডিসেন্ট পয়েন্ট দেখানো হয়েছে।
লক্ষ্য করুন যে কালো ক্ষতির বিন্দুগুলি ক্ষতির বক্ররেখার সঠিক আকৃতি তৈরি করে: ধীরে ধীরে ঢালু হওয়ার আগে একটি খাড়া পতন, যতক্ষণ না তারা ক্ষতির পৃষ্ঠের সর্বনিম্ন বিন্দুতে পৌঁছায়।
এটা মনে রাখা গুরুত্বপূর্ণ যে মডেলটি প্রায় কখনই প্রতিটি ওজন এবং পক্ষপাতের জন্য সঠিক সর্বনিম্ন মান খুঁজে পায় না, বরং এর খুব কাছাকাছি একটি মান খুঁজে পায়। এটাও মনে রাখা গুরুত্বপূর্ণ যে ওজন এবং পক্ষপাতের জন্য সর্বনিম্ন মান শূন্য ক্ষতির সাথে সঙ্গতিপূর্ণ নয়, শুধুমাত্র একটি মান যা সেই প্যারামিটারের জন্য সর্বনিম্ন ক্ষতি তৈরি করে।
ওজন এবং পক্ষপাতের মান ব্যবহার করে যা সর্বনিম্ন ক্ষতি করে - এই ক্ষেত্রে -৫.৪৪ ওজন এবং ৩৫.৯৪ পক্ষপাত - আমরা মডেলটি গ্রাফ করতে পারি যাতে দেখা যায় যে এটি ডেটার সাথে কতটা ভালভাবে খাপ খায়:
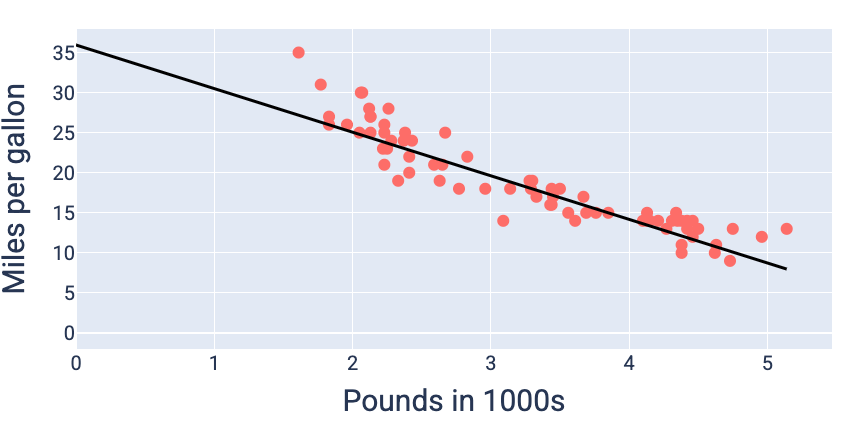
চিত্র ১৯। ওজন এবং পক্ষপাতের মান ব্যবহার করে মডেলটি গ্রাফ করা হয়েছে যা সর্বনিম্ন ক্ষতি করে।
এই ডেটাসেটের জন্য এটিই সেরা মডেল হবে কারণ অন্য কোনও ওজন এবং পক্ষপাতের মান কম ক্ষতি সহ একটি মডেল তৈরি করে না।
