O gradiente descendente é uma técnica matemática que encontra de forma iterativa as ponderações e o viés que produzem o modelo com a menor perda. O gradiente descendente encontra o melhor peso e viés repetindo o seguinte processo para várias iterações definidas pelo usuário.
O modelo começa o treinamento com pesos e vieses aleatórios próximos de zero e repete as seguintes etapas:
Calcule a perda com o peso e o viés atuais.
Determine a direção para mover os pesos e o viés que reduzem a perda.
Mova os valores de peso e viés um pouco na direção que reduz a perda.
Volte à etapa 1 e repita o processo até que o modelo não consiga mais reduzir a perda.
O diagrama abaixo descreve as etapas iterativas que o gradiente descendente realiza para encontrar as ponderações e o viés que produzem o modelo com a menor perda.
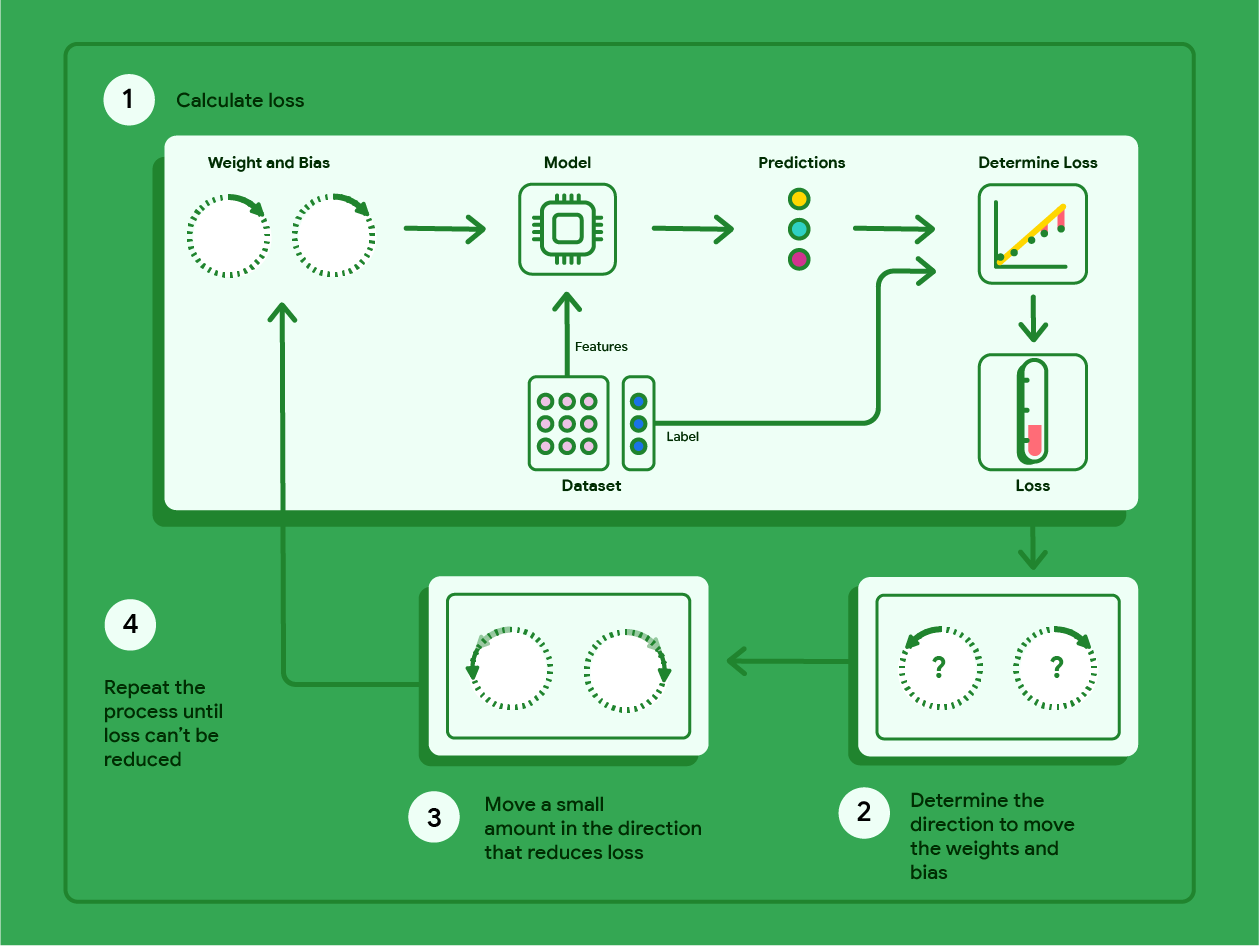
Figura 11. O gradiente descendente é um processo iterativo que encontra os pesos e o viés que produzem o modelo com a menor perda.
Clique no ícone de adição para saber mais sobre a matemática por trás da descida do gradiente.
Em um nível concreto, podemos analisar as etapas de gradiente descendente usando um pequeno conjunto de dados com sete exemplos de peso de um carro em libras e sua classificação de milhas por galão:
| Libras em milhares (recurso) | Milhas por galão (rótulo) |
|---|---|
| 3.5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
- O modelo começa o treinamento definindo o peso e o viés como zero:
- Calcule a perda de EQM com os parâmetros atuais do modelo:
- Calcule a inclinação da tangente à função de perda em cada peso e o viés:
- Mova um pouco na direção da inclinação negativa para receber o próximo peso e viés. Por enquanto, vamos definir arbitrariamente o "valor pequeno" como 0,01:
Clique no ícone de adição para saber como calcular a inclinação.
Para conseguir a inclinação das linhas tangentes ao peso e ao viés, pegamos a derivada da função de perda em relação ao peso e ao viés e resolvemos as equações.
Vamos escrever a equação para fazer uma previsão como:
$ f_{w,b}(x) = (w*x)+b $.
Vamos escrever o valor real como: $ y $.
Vamos calcular o MSE usando:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
em que $i$ representa o $iésimo$ exemplo de treinamento e $M$ representa
o número de exemplos.
A derivada da função de perda em relação ao peso é escrita como:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
e é avaliada como:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
Primeiro, somamos cada valor previsto menos o valor real e multiplicamos por duas vezes o valor do atributo. Em seguida, dividimos a soma pelo número de exemplos. O resultado é a inclinação da reta tangente ao valor do peso.
Se resolvermos essa equação com um peso e um viés iguais a zero, vamos receber -119,7 para a inclinação da linha.
Derivada de viés
A derivada da função de perda em relação ao viés é escrita como:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
e é avaliada como:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
Primeiro, somamos cada valor previsto menos o valor real e multiplicamos por dois. Em seguida, dividimos a soma pelo número de exemplos. O resultado é a inclinação da linha tangente ao valor do viés.
Se resolvermos essa equação com um peso e um viés iguais a zero, vamos ter -34,3 para a inclinação da linha.
Use o novo peso e viés para calcular a perda e repita. Concluindo o processo para seis iterações, teríamos os seguintes pesos, vieses e perdas:
| Iteração | Peso | Viés | Perda (EQM) |
|---|---|---|---|
| 1 | 0 | 0 | 303,71 |
| 2 | 1.20 | 0.34 | 170,84 |
| 3 | 2,05 | 0,59 | 103.17 |
| 4 | 2,66 | 0,78 | 68,70 |
| 5 | 3,09 | 0,91 | 51,13 |
| 6 | 3,40 | 1.01 | 42,17 |
Você pode ver que a perda diminui com cada peso e viés atualizados. Neste exemplo, paramos após seis iterações. Na prática, um modelo é treinado até convergir. Quando um modelo converge, iterações adicionais não reduzem mais a perda porque a descida do gradiente encontrou as ponderações e o viés que quase minimizam a perda.
Se o treinamento do modelo continuar após a convergência, a perda começará a variar em pequenas quantidades à medida que o modelo atualiza continuamente os parâmetros em torno dos valores mais baixos. Isso pode dificultar a verificação de que o modelo realmente convergiu. Para confirmar se o modelo convergiu, continue treinando até que a perda se estabilize.
Convergência do modelo e curvas de perda
Ao treinar um modelo, você geralmente analisa uma curva de perda para determinar se o modelo convergiu. A curva de perda mostra como a perda muda à medida que o modelo é treinado. Veja a seguir uma curva de perda típica. A perda está no eixo y e as iterações estão no eixo x:
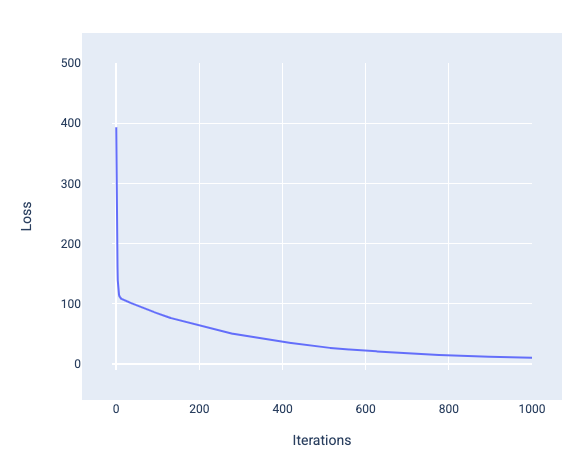
Figura 12. Curva de perda mostrando a convergência do modelo em torno da marca da 1.000ª iteração.
É possível notar que a perda diminui drasticamente durante as primeiras iterações e depois gradualmente até se estabilizar por volta da marca de 1.000 iterações. Após 1.000 iterações, podemos ter certeza de que o modelo convergiu.
Nas figuras a seguir, mostramos o modelo em três pontos durante o processo de treinamento: início, meio e fim. A visualização do estado do modelo em snapshots durante o processo de treinamento consolida a relação entre a atualização dos pesos e do viés, a redução da perda e a convergência do modelo.
Nas figuras, usamos os pesos e o viés derivados em uma iteração específica para representar o modelo. No gráfico com os pontos de dados e o snapshot do modelo, as linhas de perda azuis do modelo até os pontos de dados mostram a quantidade de perda. Quanto mais longas as linhas, maior a perda.
Na figura a seguir, podemos ver que, por volta da segunda iteração, o modelo não seria bom para fazer previsões devido à alta quantidade de perda.
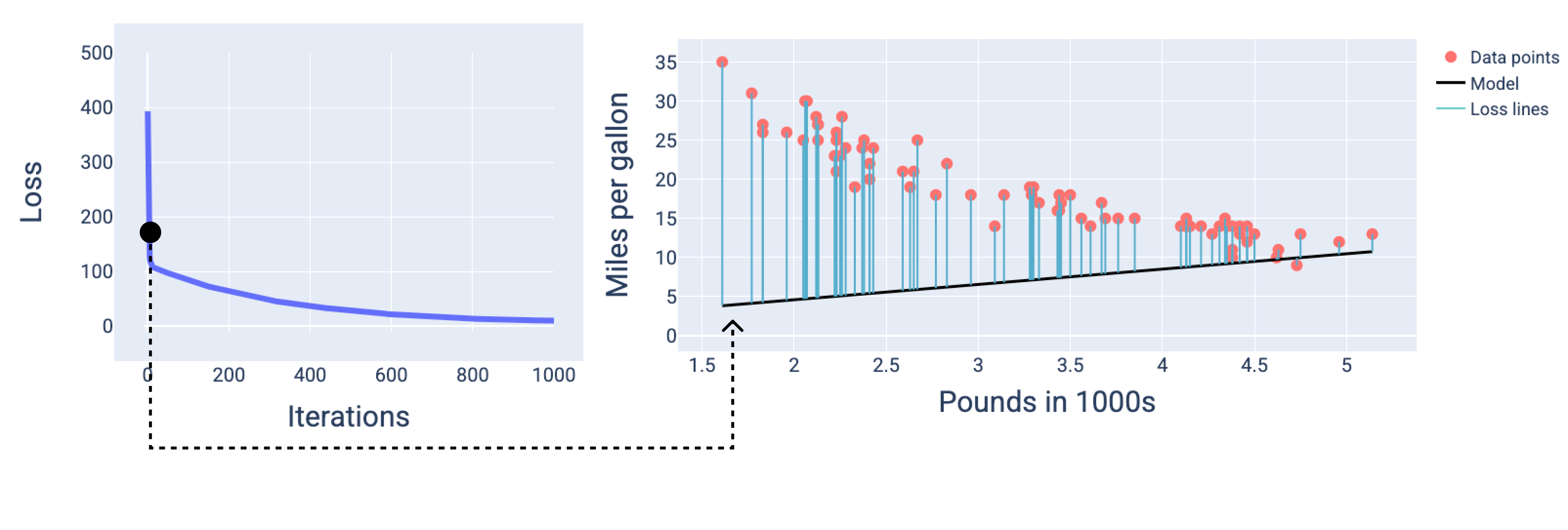
Figura 13. Curva de perda e snapshot do modelo no início do processo de treinamento.
Por volta da 400ª iteração, podemos ver que a descida do gradiente encontrou o peso e o viés que produzem um modelo melhor.
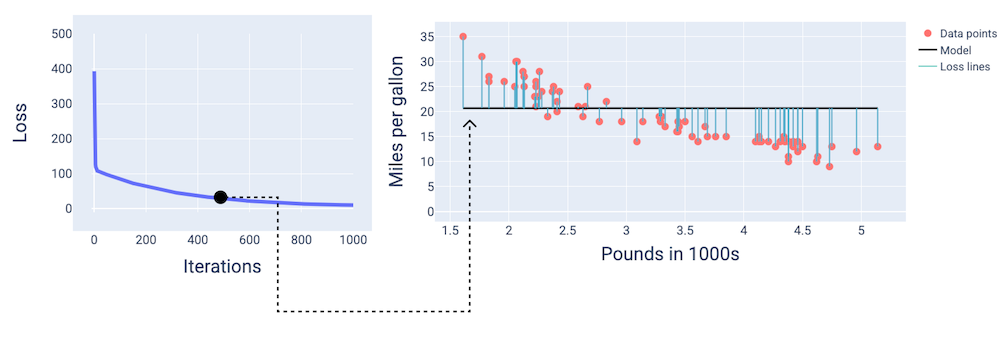
Figura 14. Curva de perda e snapshot do modelo na metade do treinamento.
Por volta da milésima iteração, o modelo converge, produzindo um modelo com a menor perda possível.
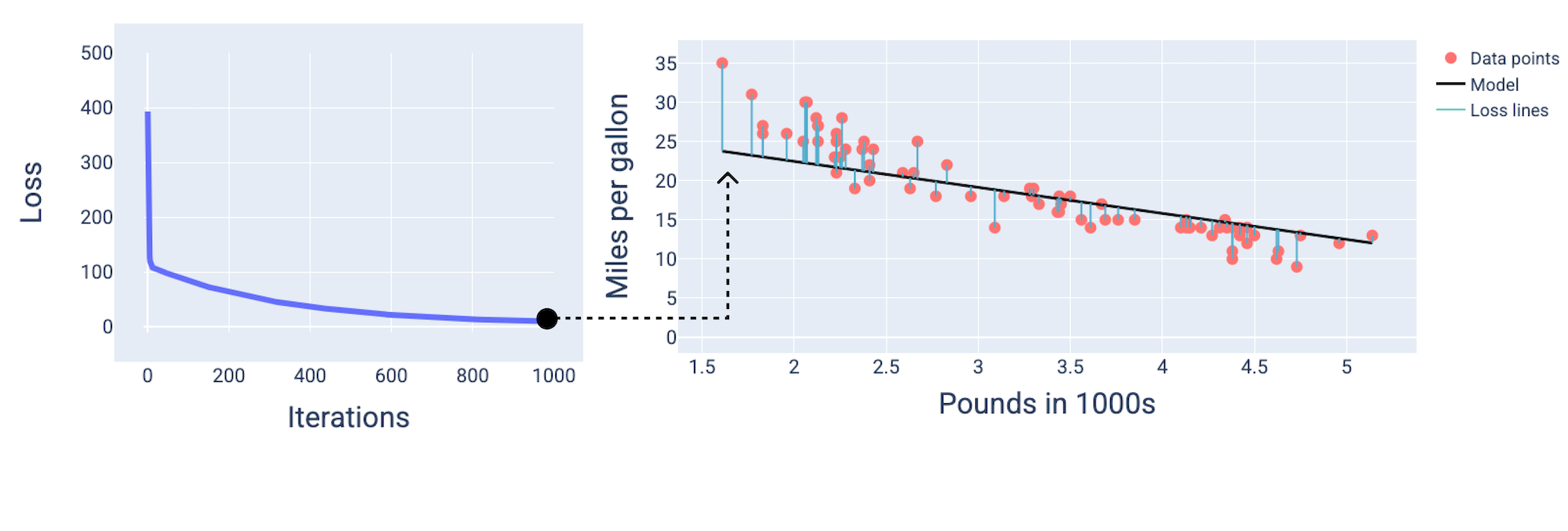
Figura 15. Curva de perda e snapshot do modelo perto do final do processo de treinamento.
Exercício: teste de conhecimentos
Convergência e funções convexas
As funções de perda para modelos lineares sempre produzem uma superfície convexa. Como resultado dessa propriedade, quando um modelo de regressão linear converge, sabemos que ele encontrou os pesos e o viés que produzem a menor perda.
Se representarmos a superfície de perda de um modelo com um recurso, vamos ver o formato convexo dela. A seguir, apresentamos a superfície de perda para um conjunto de dados hipotético de milhas por galão. O peso está no eixo x, o viés no eixo y e a perda no eixo z:
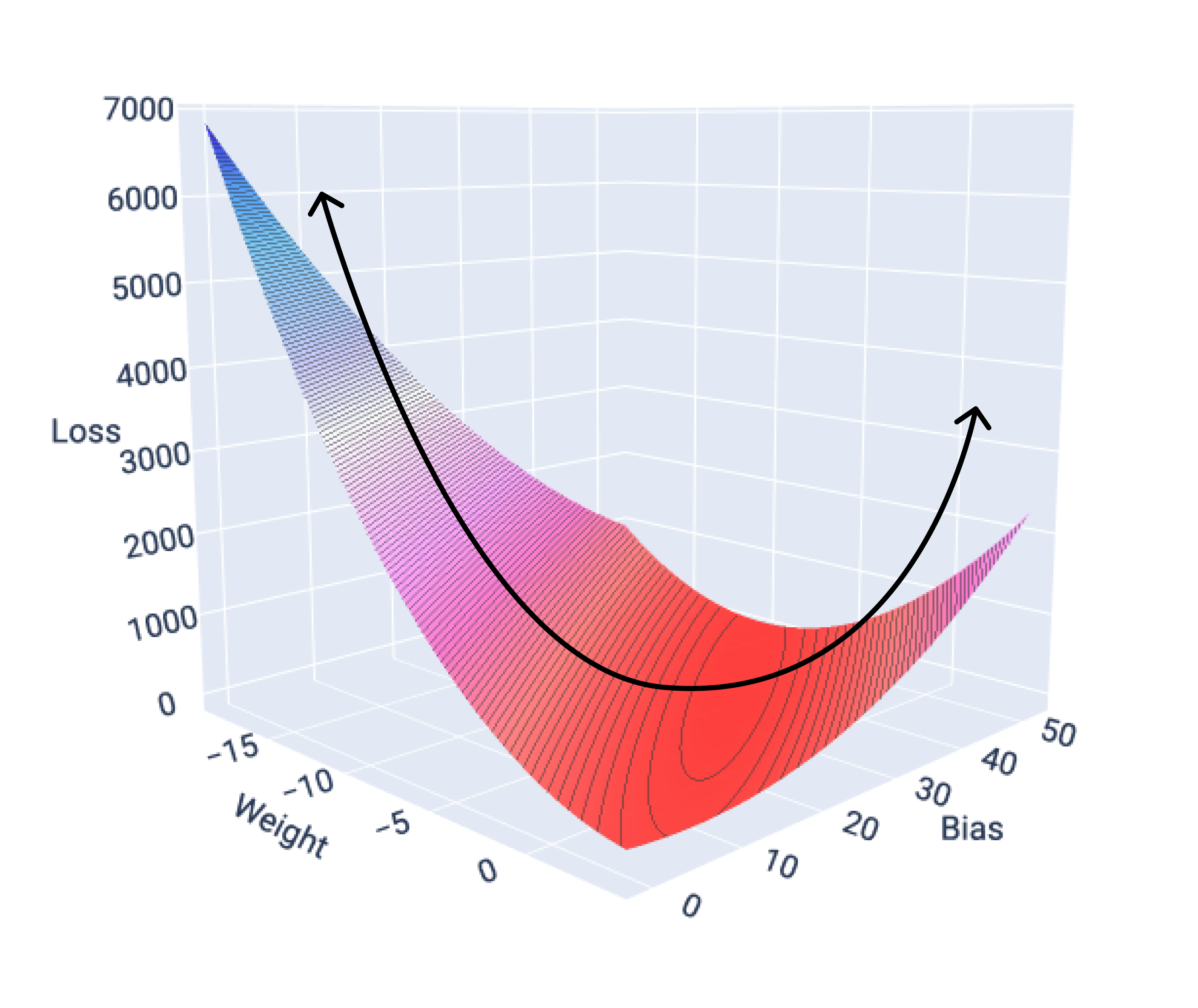
Figura 16. Superfície de perda que mostra sua forma convexa.
Neste exemplo, um peso de -5,44 e um bias de 35,94 produzem a menor perda em 5,54:
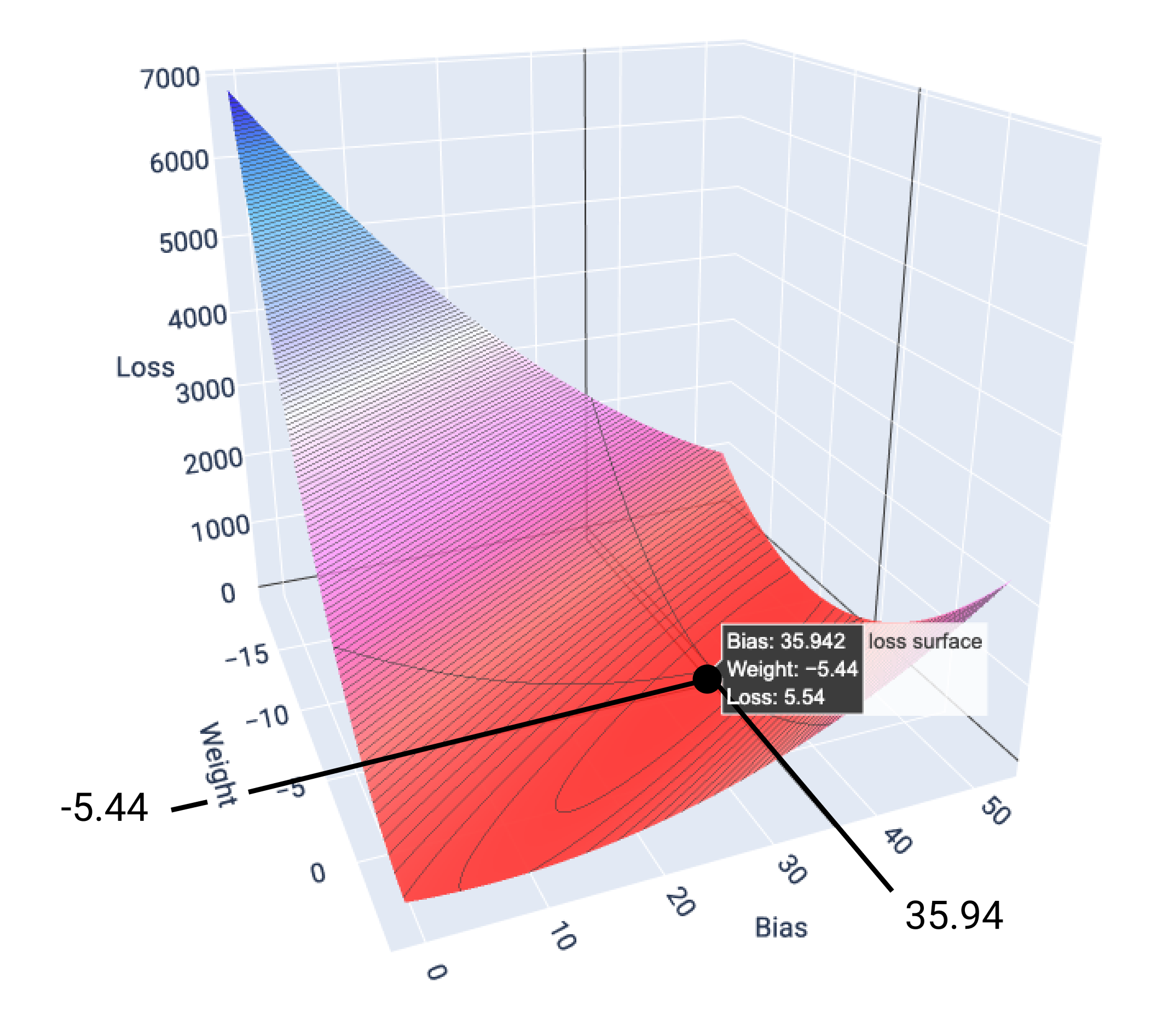
Figura 17. Superfície de perda mostrando os valores de peso e viés que produzem a menor perda.
Um modelo linear converge quando a perda mínima é encontrada. Portanto, iterações adicionais apenas fazem com que a descida do gradiente mova os valores de peso e viés em quantidades muito pequenas ao redor do mínimo. Se representarmos os pesos e os pontos de bias durante a descida do gradiente, os pontos vão parecer uma bola rolando por uma colina, parando finalmente no ponto em que não há mais inclinação para baixo.
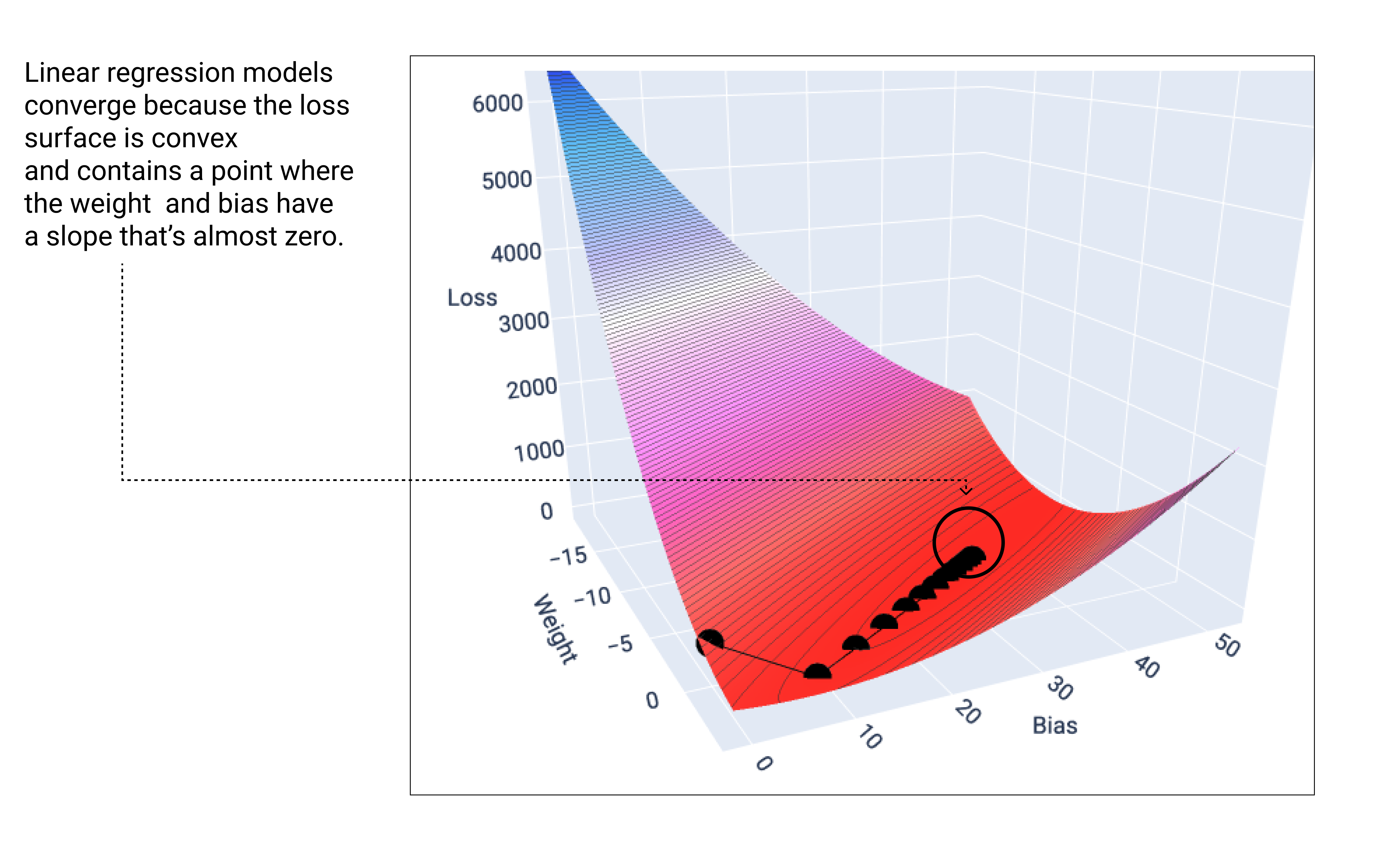
Figura 18. Gráfico de perda mostrando pontos de descida de gradiente parando no ponto mais baixo do gráfico.
Observe que os pontos de perda pretos criam a forma exata da curva de perda: um declínio acentuado antes de diminuir gradualmente até atingir o ponto mais baixo na superfície de perda.
É importante observar que o modelo quase nunca encontra o mínimo exato para cada peso e viés, mas encontra um valor muito próximo a ele. Também é importante observar que o mínimo para os pesos e o viés não corresponde a perda zero, apenas a um valor que produz a menor perda para esse parâmetro.
Usando os valores de peso e viés que produzem a menor perda (neste caso, um peso de -5,44 e um viés de 35,94), podemos representar o modelo para ver o quanto ele se ajusta aos dados:
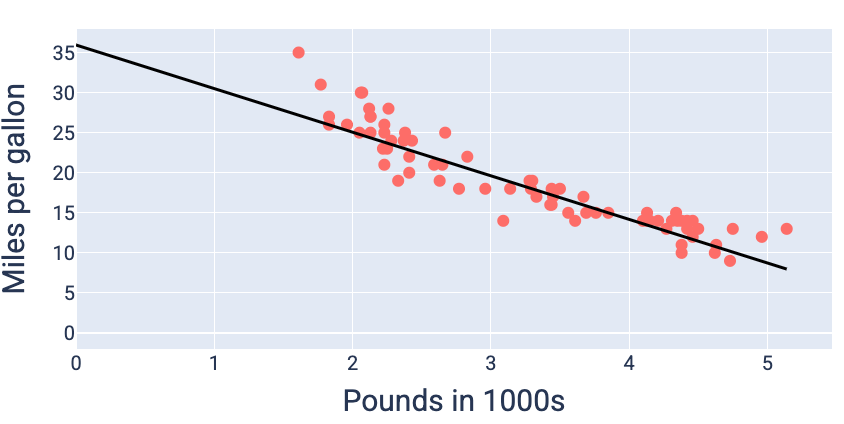
Figura 19. Modelo representado usando os valores de peso e viés que produzem a menor perda.
Esse seria o melhor modelo para esse conjunto de dados porque nenhum outro valor de peso e viés produz um modelo com perda menor.
