การไล่ระดับความชันเป็นเทคนิคทางคณิตศาสตร์ที่ค้นหาน้ำหนักและอคติซ้ำๆ ซึ่งจะสร้างโมเดลที่มีการสูญเสียต่ำสุด การไล่ระดับสีจะค้นหาน้ำหนักและอคติที่ดีที่สุด โดยทำกระบวนการต่อไปนี้ซ้ำตามจำนวนการทำซ้ำที่ผู้ใช้กำหนด
โมเดลจะเริ่มฝึกโดยใช้ค่าถ่วงน้ำหนักและอคติแบบสุ่มที่ใกล้ 0 จากนั้นจะทำซ้ำขั้นตอนต่อไปนี้
คำนวณการสูญเสียด้วยน้ำหนักและอคติปัจจุบัน
กำหนดทิศทางที่จะย้ายน้ำหนักและอคติที่ลดการสูญเสีย
เลื่อนค่าถ่วงน้ำหนักและค่าอคติเล็กน้อยในทิศทางที่ลด การสูญเสีย
กลับไปที่ขั้นตอนที่ 1 และทำซ้ำจนกว่าโมเดลจะลด การสูญเสียไม่ได้อีก
แผนภาพด้านล่างแสดงขั้นตอนการวนซ้ำที่การไล่ระดับความชันแบบวนซ้ำใช้เพื่อค้นหา น้ำหนักและอคติที่สร้างโมเดลที่มีการสูญเสียต่ำที่สุด
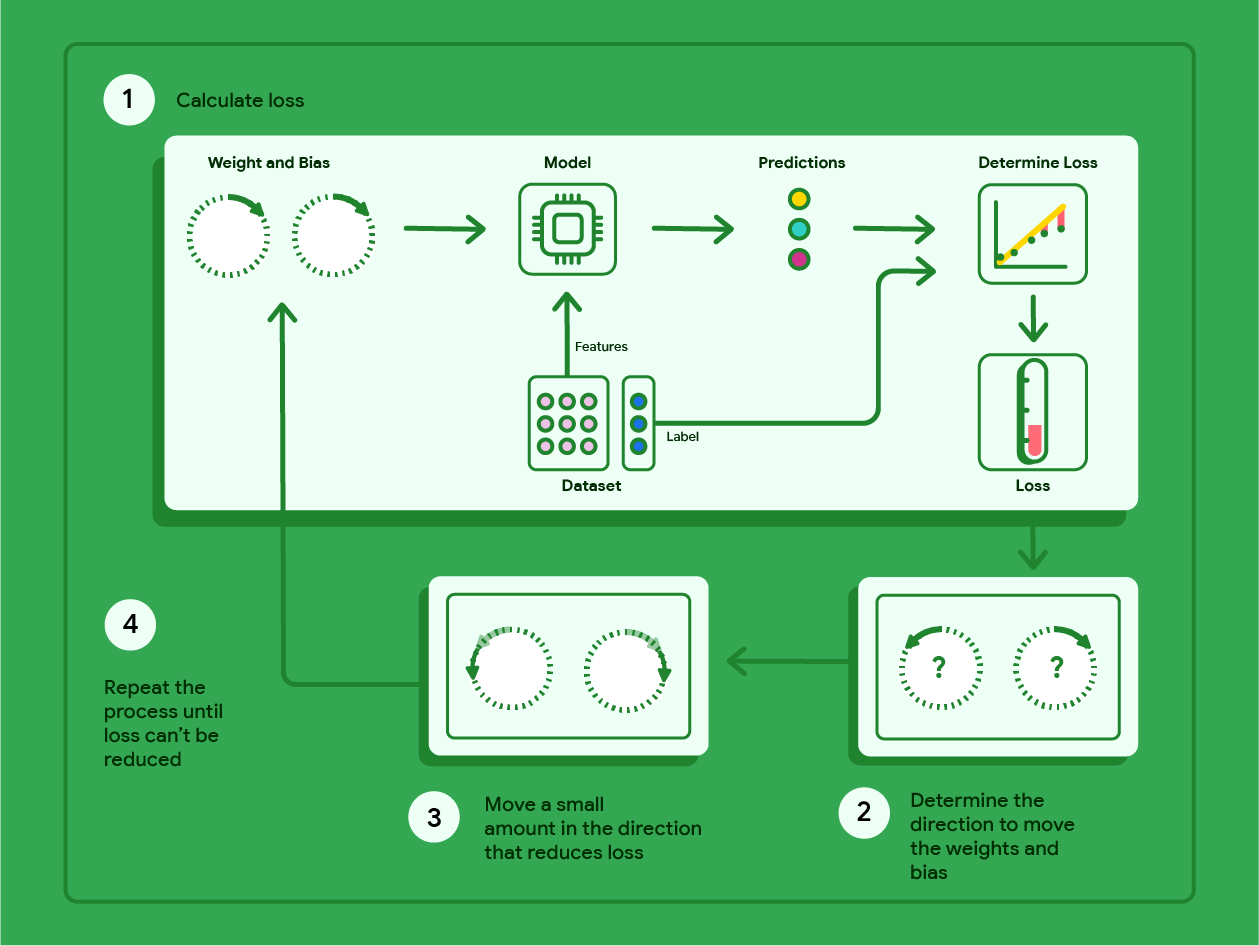
รูปที่ 11 การไล่ระดับความชันเป็นกระบวนการที่ต้องทำซ้ำๆ ซึ่งจะค้นหาน้ำหนัก และอคติที่สร้างโมเดลที่มี Loss ต่ำที่สุด
คลิกไอคอนเครื่องหมายบวกเพื่อดูข้อมูลเพิ่มเติมเกี่ยวกับคณิตศาสตร์เบื้องหลังการไล่ระดับสี
ในระดับที่เจาะจง เราสามารถดูขั้นตอนการไล่ระดับการไล่ระดับสี โดยใช้ชุดข้อมูลประสิทธิภาพการใช้เชื้อเพลิงขนาดเล็กต่อไปนี้ที่มีตัวอย่าง 7 รายการ และ ข้อผิดพลาดกำลังสองเฉลี่ย (MSE) เป็นเมตริกการสูญเสีย
| ปอนด์ในหน่วยพัน (ฟีเจอร์) | ไมล์ต่อแกลลอน (ป้ายกำกับ) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- โมเดลจะเริ่มฝึกโดยตั้งค่าน้ำหนักและอคติเป็น 0
- คำนวณการสูญเสีย MSE ด้วยพารามิเตอร์โมเดลปัจจุบัน
- คำนวณความชันของเส้นสัมผัสฟังก์ชันการสูญเสียที่น้ำหนักแต่ละรายการ และอคติ
- เลื่อนไปเล็กน้อยในทิศทางของความชันที่เป็นลบเพื่อรับ น้ำหนักและอคติถัดไป ในตอนนี้ เราจะกำหนด "จำนวนเล็กน้อย" เป็น 0.01 โดยพลการ
คลิกไอคอนเครื่องหมายบวกเพื่อดูข้อมูลเกี่ยวกับการคำนวณความชัน
หากต้องการหาความชันของเส้นสัมผัสกับน้ำหนักและ อคติ เราจะหาอนุพันธ์ของฟังก์ชันการสูญเสียเทียบกับ น้ำหนักและอคติ แล้วแก้สมการ
เราจะเขียนสมการสำหรับการคาดการณ์ได้ดังนี้
$ f_{w,b}(x) = (w*x)+b $
เราจะเขียนค่าจริงเป็น $ y $
เราจะคำนวณ MSE โดยใช้
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
โดยที่ $i$ แสดงตัวอย่างการฝึกที่ $i$ และ $M$ แสดง
จำนวนตัวอย่าง
อนุพันธ์ของฟังก์ชันการสูญเสียที่เทียบกับน้ำหนักเขียนได้ดังนี้
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
และประเมินได้เป็น
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
ก่อนอื่นเราจะบวกค่าที่คาดการณ์แต่ละค่าลบด้วยค่าจริง แล้วคูณด้วยค่าฟีเจอร์ 2 เท่า จากนั้นเราจะนำผลรวมไปหารด้วยจำนวนตัวอย่าง ผลลัพธ์คือความชันของเส้นสัมผัสกับค่า ของน้ำหนัก
หากเราแก้สมการนี้โดยกำหนดให้น้ำหนักและอคติเท่ากับ 0 เราจะได้ความชันของเส้นเท่ากับ -119.7
อนุพันธ์ของอคติ
อนุพันธ์ของฟังก์ชันการสูญเสียที่เทียบกับ
อคติเขียนได้ดังนี้
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
และประเมินเป็น
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
ก่อนอื่นเราจะบวกค่าที่คาดการณ์แต่ละค่าลบด้วยค่าจริง แล้วคูณด้วย 2 จากนั้นเราจะหารผลรวมด้วย จำนวนตัวอย่าง ผลลัพธ์คือความชันของเส้น สัมผัสกับค่าของอคติ
หากเราแก้สมการนี้โดยให้น้ำหนักและค่าอคติเท่ากับ 0 เราจะได้ -34.3 สำหรับความชันของเส้น
ใช้น้ำหนักและความเอนเอียงใหม่เพื่อคำนวณการสูญเสียและการทำซ้ำ เมื่อทำกระบวนการนี้ซ้ำ 6 ครั้ง เราจะได้ค่าถ่วงน้ำหนัก อคติ และการสูญเสียดังนี้
| การทำซ้ำ | น้ำหนัก | อคติ | Loss (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
คุณจะเห็นว่าการสูญเสียลดลงเมื่อมีการอัปเดตน้ำหนักและความเอนเอียงแต่ละครั้ง ในตัวอย่างนี้ เราหยุดหลังจากทำซ้ำ 6 ครั้ง ในทางปฏิบัติ โมเดลจะ ฝึกจนกว่าจะ บรรจบกัน เมื่อโมเดลบรรจบกัน การทำซ้ำเพิ่มเติมจะไม่ลด Loss มากขึ้น เนื่องจากการไล่ระดับความชันได้ค้นพบนํ้าหนักและอคติที่เกือบจะ ลด Loss ให้เหลือน้อยที่สุดแล้ว
หากโมเดลยังคงฝึกต่อไปหลังจากบรรลุการบรรจบกันแล้ว Loss จะเริ่ม ผันผวนเล็กน้อยเนื่องจากโมเดลจะอัปเดต พารามิเตอร์อย่างต่อเนื่องรอบค่าต่ำสุด ซึ่งอาจทำให้ตรวจสอบได้ยากว่าโมเดลบรรจบกันจริงหรือไม่ หากต้องการยืนยันว่าโมเดล บรรจบกันแล้ว คุณจะต้องฝึกต่อไปจนกว่าการสูญเสียจะ คงที่
เส้นโค้งการบรรจบกันของโมเดลและเส้นโค้งการสูญเสีย
เมื่อฝึกโมเดล คุณมักจะดูเส้นโค้ง การสูญเสียเพื่อพิจารณาว่าโมเดลบรรจบกันหรือไม่ เส้นโค้งการสูญเสียแสดง การเปลี่ยนแปลงของการสูญเสียเมื่อโมเดลได้รับการฝึก ต่อไปนี้คือลักษณะของเส้นโค้งการสูญเสียโดยทั่วไป การสูญเสียจะอยู่บนแกน Y และการทำซ้ำจะอยู่บนแกน X
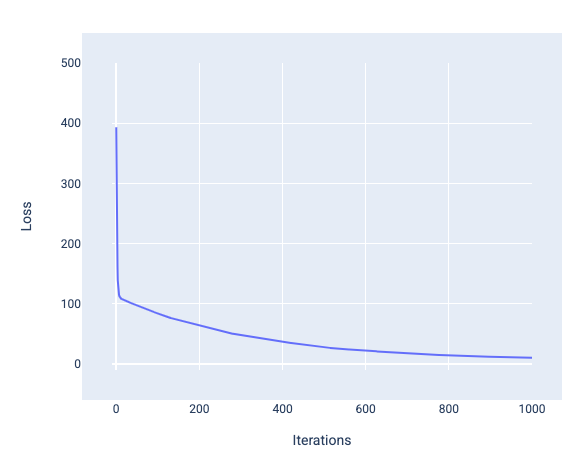
รูปที่ 12 เส้นโค้งการสูญเสียที่แสดงโมเดลที่บรรจบกันรอบเครื่องหมายการทำซ้ำครั้งที่ 1,000
คุณจะเห็นว่าการสูญเสียลดลงอย่างมากในช่วง 2-3 การทำซ้ำแรก จากนั้นจะค่อยๆ ลดลงก่อนที่จะคงที่เมื่อถึงการทำซ้ำที่ประมาณ 1,000 หลังจากทำซ้ำ 1,000 ครั้ง เราจะมั่นใจได้ว่าโมเดล บรรจบกันแล้ว
ในรูปต่อไปนี้ เราจะวาดโมเดลที่ 3 จุดในระหว่างกระบวนการฝึก ได้แก่ จุดเริ่มต้น จุดกึ่งกลาง และจุดสิ้นสุด การแสดงภาพสถานะของโมเดล ที่สแนปช็อตระหว่างกระบวนการฝึกจะช่วยเสริมความเชื่อมโยงระหว่างการอัปเดต น้ำหนักและอคติ การลดการสูญเสีย และการบรรจบกันของโมเดล
ในรูปภาพ เราใช้น้ำหนักและอคติที่ได้มาในการทำซ้ำที่เฉพาะเจาะจงเพื่อ แสดงถึงโมเดล ในกราฟที่มีจุดข้อมูลและสแนปชอตโมเดล เส้นการสูญเสียสีน้ำเงินจากโมเดลไปยังจุดข้อมูลจะแสดงปริมาณการสูญเสีย ยิ่งสายยาวมากเท่าใด การสูญเสียก็จะยิ่งมากขึ้นเท่านั้น
ในรูปที่ 1 เราจะเห็นว่าในรอบที่ 2 โมเดล จะคาดการณ์ได้ไม่ดีเนื่องจากค่าการสูญเสียสูง
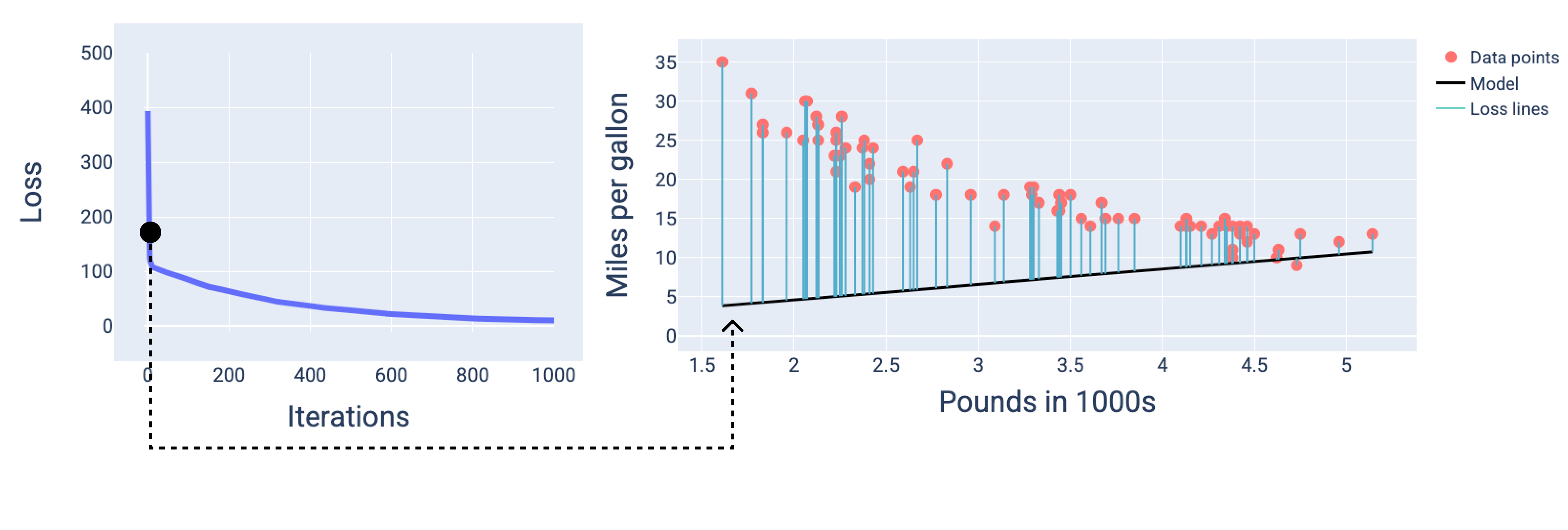
รูปที่ 13 เส้นโค้งการสูญเสียและสแนปชอตของโมเดลในช่วงเริ่มต้นของ กระบวนการฝึก
เมื่อวนซ้ำประมาณ 400 ครั้ง เราจะเห็นว่าการไล่ระดับความชันได้ค้นพบ น้ำหนักและอคติที่สร้างโมเดลที่ดีขึ้น
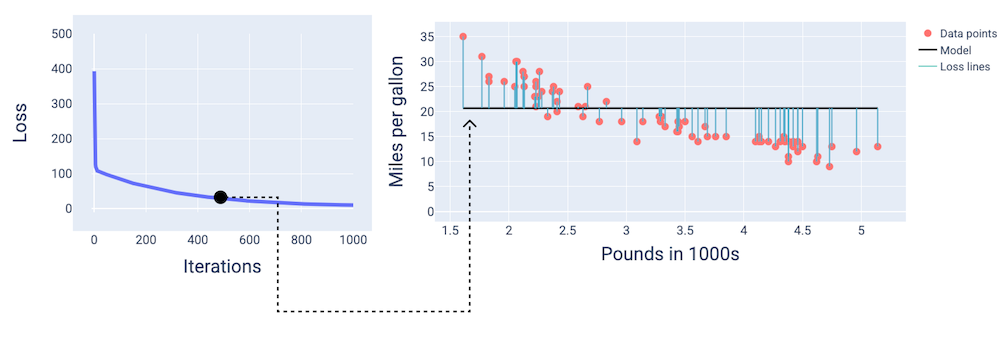
รูปที่ 14 เส้นโค้งการสูญเสียและภาพรวมของโมเดลในช่วงกลางของการฝึก
และเมื่อถึงการวนซ้ำครั้งที่ประมาณ 1,000 เราจะเห็นว่าโมเดลบรรจบกันแล้ว ซึ่งสร้างโมเดลที่มีการสูญเสียต่ำที่สุดเท่าที่จะเป็นไปได้
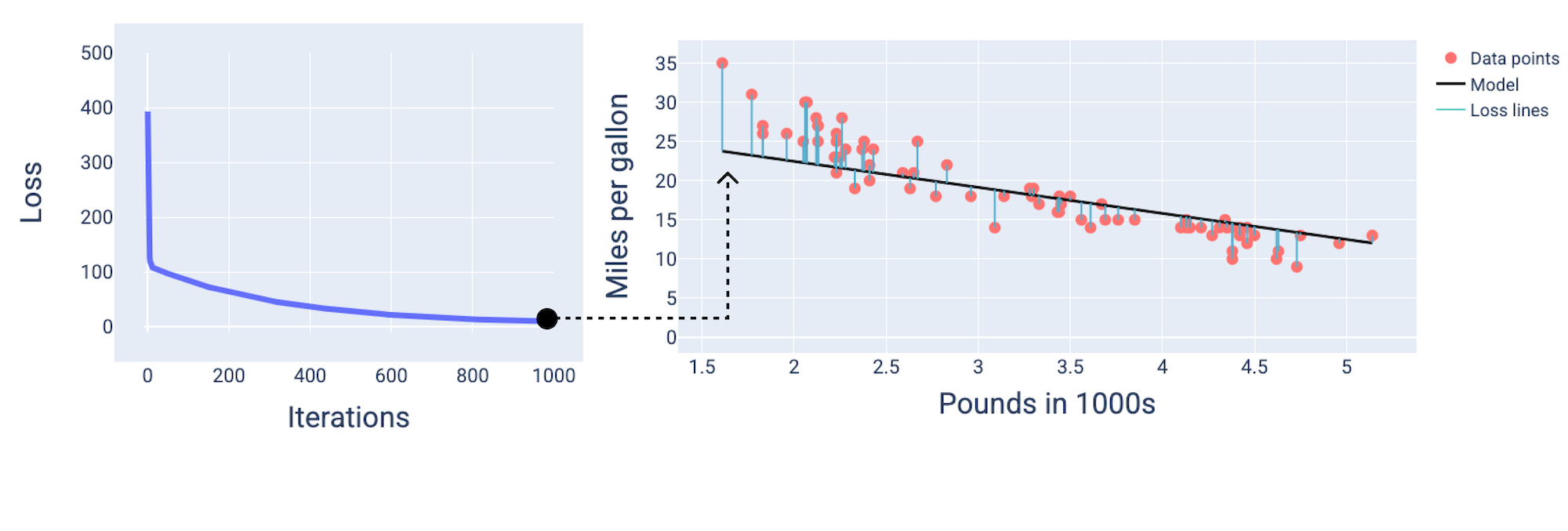
รูปที่ 15 เส้นโค้งการสูญเสียและภาพรวมของโมเดลในช่วงท้ายของกระบวนการฝึก
แบบฝึกหัด: ทดสอบความเข้าใจ
ฟังก์ชันการบรรจบกันและฟังก์ชันนูน
ฟังก์ชันการสูญเสียสำหรับโมเดลเชิงเส้นจะสร้างพื้นผิวนูนเสมอ ด้วยคุณสมบัตินี้ เมื่อโมเดลการถดถอยเชิงเส้นบรรจบกัน เราจะทราบว่าโมเดลได้ค้นหาน้ำหนักและอคติที่ทำให้เกิดการสูญเสียต่ำที่สุดแล้ว
หากเราสร้างกราฟพื้นผิวการสูญเสียสำหรับโมเดลที่มีฟีเจอร์เดียว เราจะเห็นรูปร่างนูนของพื้นผิว ต่อไปนี้คือพื้นผิวการสูญเสียสำหรับชุดข้อมูลไมล์ต่อแกลลอนสมมติ น้ำหนักอยู่บนแกน x อคติอยู่บนแกน y และการสูญเสียอยู่บน แกน z
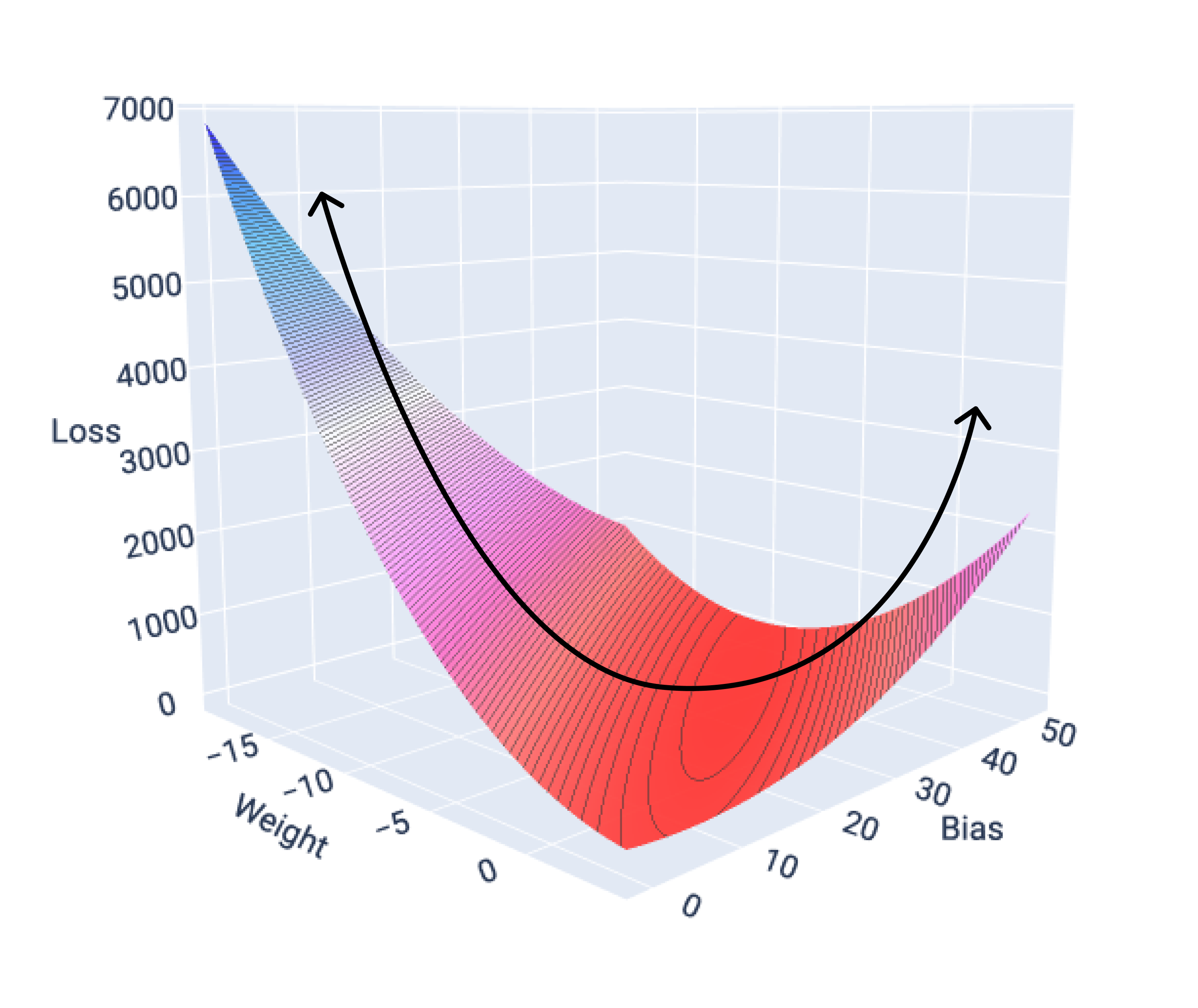
รูปที่ 16 พื้นผิวการสูญเสียที่แสดงรูปร่างนูน
ในตัวอย่างนี้ น้ำหนัก -5.44 และอคติ 35.94 ทำให้เกิดการสูญเสียต่ำสุด ที่ 5.54
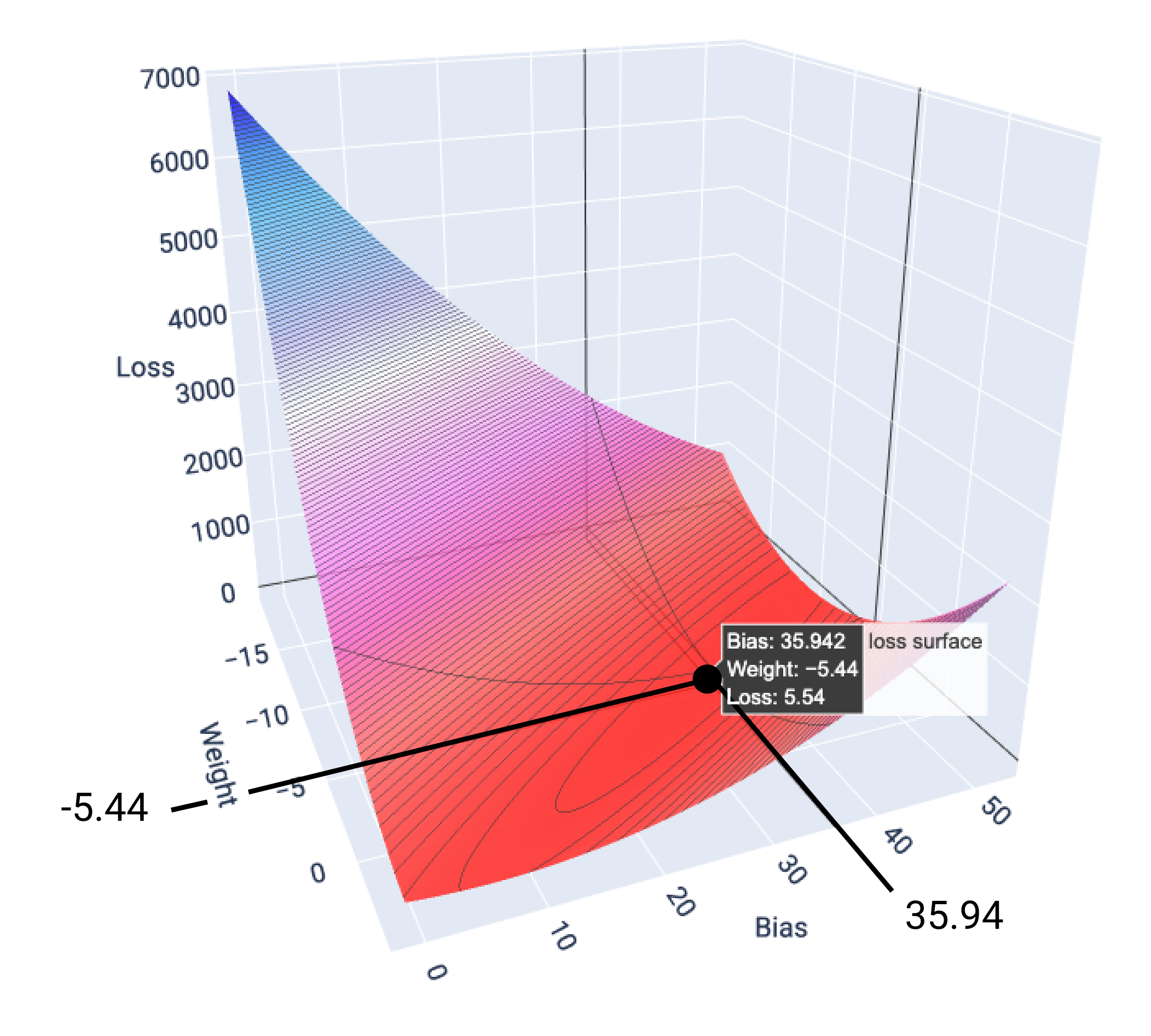
รูปที่ 17 พื้นผิวการสูญเสียแสดงค่าถ่วงน้ำหนักและค่าอคติที่ทำให้เกิดการสูญเสียต่ำสุด
โมเดลเชิงเส้นจะบรรจบกันเมื่อพบการสูญเสียขั้นต่ำ ดังนั้น การทำซ้ำเพิ่มเติมจึงทำให้การไล่ระดับความชันย้ายค่าถ่วงน้ำหนักและค่าอคติในปริมาณที่น้อยมากรอบๆ ค่าต่ำสุดเท่านั้น หากเราทำกราฟจุดน้ำหนักและอคติ ระหว่างการไล่ระดับการไล่ระดับสี จุดต่างๆ จะดูเหมือนลูกบอลกลิ้งลงเนิน และหยุดในที่สุด ณ จุดที่ไม่มีความชันลงอีก
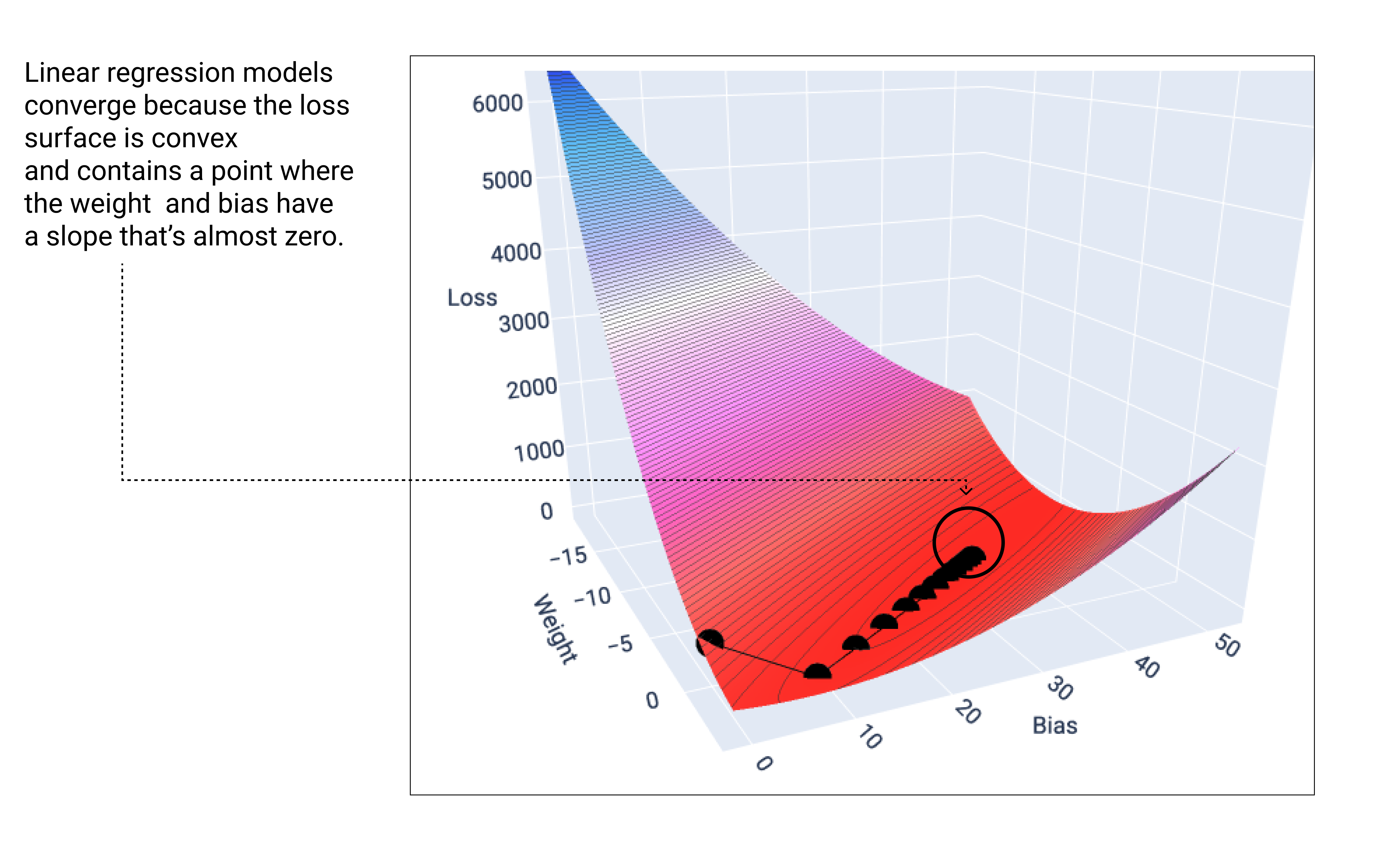
รูปที่ 18 กราฟการสูญเสียที่แสดงจุดการไล่ระดับสีหยุดที่จุดต่ำสุด บนกราฟ
โปรดสังเกตว่าจุดการสูญเสียสีดำสร้างรูปร่างที่แน่นอนของเส้นโค้งการสูญเสีย ซึ่งก็คือการลดลงอย่างรวดเร็วก่อนที่จะค่อยๆ ลดลงจนถึงจุดต่ำสุดบนพื้นผิวการสูญเสีย
โปรดทราบว่าโมเดลแทบจะไม่พบค่าต่ำสุดที่แน่นอน สำหรับน้ำหนักและอคติแต่ละรายการ แต่จะพบค่าที่ใกล้เคียงกับค่าต่ำสุดมากแทน นอกจากนี้ โปรดทราบว่าค่าต่ำสุดของน้ำหนักและอคติไม่ได้ สอดคล้องกับการสูญเสียเป็น 0 แต่เป็นค่าที่ทำให้เกิดการสูญเสียต่ำที่สุดสำหรับพารามิเตอร์นั้น
การใช้น้ำหนักและค่าอคติที่ทำให้เกิดการสูญเสียต่ำที่สุด ในกรณีนี้คือน้ำหนัก -5.44 และอคติ 35.94 เราสามารถสร้างกราฟโมเดลเพื่อดูว่าโมเดลเหมาะกับข้อมูลมากน้อยเพียงใด
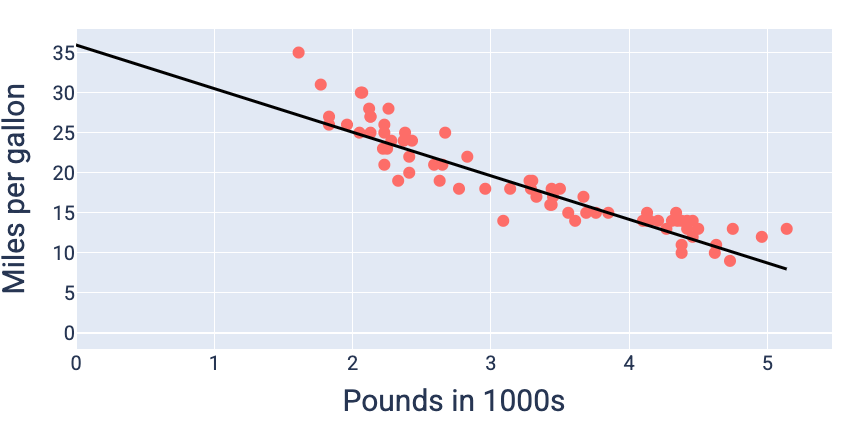
รูปที่ 19 โมเดลที่สร้างกราฟโดยใช้น้ำหนักและค่าอคติที่ทำให้เกิด การสูญเสียต่ำที่สุด
นี่จะเป็นโมเดลที่ดีที่สุดสําหรับชุดข้อมูลนี้ เนื่องจากค่าถ่วงน้ำหนักและความเอนเอียงอื่นๆ ไม่ได้สร้างโมเดลที่มีการสูญเสียต่ำกว่า
