Hồi quy tuyến tính: Phương pháp giảm độ dốc

Hạ độ dốc là một kỹ thuật toán học lặp lại để tìm ra các trọng số và độ lệch tạo ra mô hình có mức tổn thất thấp nhất. Phương pháp hạ độ dốc tìm ra trọng số và độ lệch tốt nhất bằng cách lặp lại quy trình sau đây cho một số lần lặp do người dùng xác định.

Mô hình bắt đầu huấn luyện với các trọng số và độ lệch ngẫu nhiên gần bằng 0, sau đó lặp lại các bước sau:

1. Tính toán mức tổn thất với trọng số và độ lệch hiện tại.

2. Xác định hướng di chuyển các trọng số và độ lệch giúp giảm tổn thất.

3. Di chuyển các giá trị trọng số và độ lệch một lượng nhỏ theo hướng làm giảm tổn thất.

4. Quay lại bước một và lặp lại quy trình cho đến khi mô hình không thể giảm tổn thất thêm nữa.

Sơ đồ dưới đây trình bày các bước lặp lại mà phương pháp hạ độ dốc thực hiện để tìm ra các trọng số và độ lệch tạo ra mô hình có mức tổn thất thấp nhất.

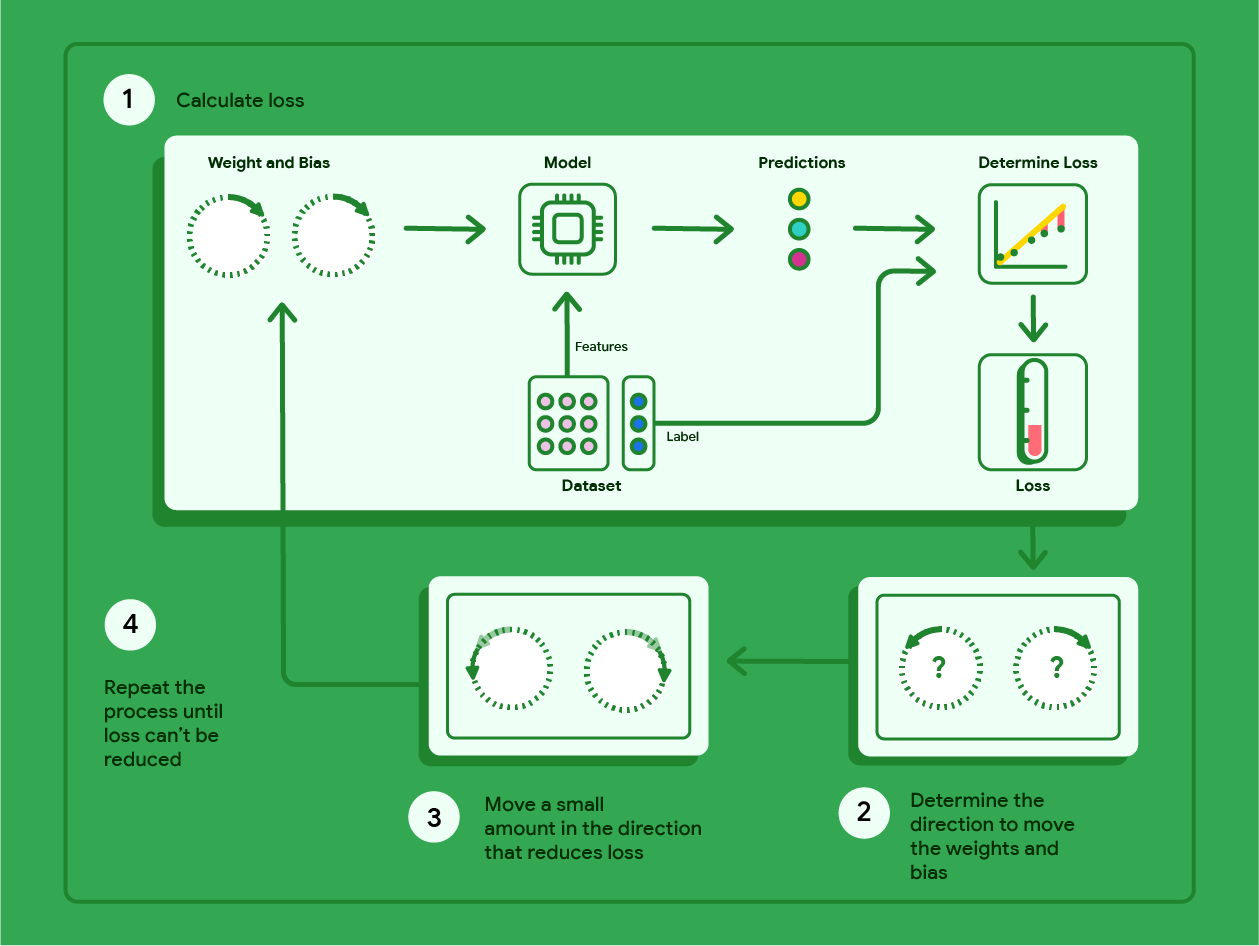
Hình 11 Hạ dốc là một quy trình lặp lại để tìm ra các trọng số và độ lệch tạo ra mô hình có mức tổn thất thấp nhất.

Nhấp vào biểu tượng dấu cộng để tìm hiểu thêm về phép toán đằng sau phương pháp hạ dốc.

Ở cấp độ cụ thể, chúng ta có thể xem xét các bước hạ độ dốc bằng cách sử dụng một tập dữ liệu nhỏ gồm 7 ví dụ về độ nặng của một chiếc ô tô tính bằng pound và mức tiêu thụ nhiên liệu tính bằng dặm trên một gallon:

Pao (tính bằng nghìn) (đối tượng)	Dặm trên ga lông (nhãn)
3,5	18
3,69	15
3,44	18
3,43	16
4,34	15
4,42	14
2,37	24

1. Mô hình bắt đầu huấn luyện bằng cách đặt trọng số và độ lệch thành 0:
$$ \small{Weight:\ 0} $$ $$ \small{Bias:\ 0} $$ $$ \small{y = 0 + 0(x_1)} $$
2. Tính toán tổn thất MSE bằng các tham số mô hình hiện tại:
$$ \small{Loss = \frac{(18-0)^2 + (15-0)^2 + (18-0)^2 + (16-0)^2 + (15-0)^2 + (14-0)^2 + (24-0)^2}{7}} $$ $$ \small{Loss= 303.71} $$
3. Tính độ dốc của đường tiếp tuyến với hàm tổn thất tại mỗi trọng số và độ lệch:
$$ \small{Weight\ slope: -119.7} $$ $$ \small{Bias\ slope: -34.3} $$

Nhấp vào biểu tượng dấu cộng để tìm hiểu về cách tính độ dốc.

Để tìm độ dốc cho các đường tiếp tuyến với trọng số và độ lệch, chúng ta lấy đạo hàm của hàm tổn thất theo trọng số và độ lệch, sau đó giải các phương trình.

Chúng ta sẽ viết phương trình để dự đoán như sau:
$ f_{w,b}(x) = (w*x)+b $.

Chúng ta sẽ viết giá trị thực là: $ y $.

Chúng ta sẽ tính MSE bằng cách sử dụng:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
trong đó $i$ biểu thị ví dụ huấn luyện thứ $i$ và $M$ biểu thị số lượng ví dụ.

Đạo hàm trọng số

Đạo hàm của hàm tổn thất theo trọng số được viết là:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $


và được đánh giá là:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $

Trước tiên, chúng ta tính tổng từng giá trị dự đoán trừ đi giá trị thực tế, sau đó nhân kết quả với hai lần giá trị của đối tượng. Sau đó, chúng ta chia tổng này cho số lượng ví dụ. Kết quả là độ dốc của đường tiếp tuyến với giá trị của trọng số.

Nếu giải phương trình này với trọng số và độ lệch bằng 0, chúng ta sẽ được -119,7 cho độ dốc của đường thẳng.

Đạo hàm thiên vị

Đạo hàm của hàm tổn thất theo độ lệch được viết là:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $


và được đánh giá là:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $

Trước tiên, chúng ta cộng từng giá trị dự đoán trừ đi giá trị thực tế, sau đó nhân kết quả với 2. Sau đó, chúng ta chia tổng này cho số lượng ví dụ. Kết quả là độ dốc của đường tiếp tuyến với giá trị của độ lệch.

Nếu giải phương trình này với trọng số và độ lệch bằng 0, chúng ta sẽ được -34,3 cho độ dốc của đường thẳng.

4. Di chuyển một lượng nhỏ theo hướng dốc âm để nhận được trọng số và độ lệch tiếp theo. Hiện tại, chúng ta sẽ tuỳ ý xác định "số tiền nhỏ" là 0,01:
$$ \small{New\ weight = old\ weight - (small\ amount * weight\ slope)} $$ $$ \small{New\ bias = old\ bias - (small\ amount * bias\ slope)} $$ $$ \small{New\ weight = 0 - (0.01)*(-119.7)} $$ $$ \small{New\ bias = 0 - (0.01)*(-34.3)} $$ $$ \small{New\ weight = 1.2} $$ $$ \small{New\ bias = 0.34} $$

Sử dụng trọng số và độ lệch mới để tính toán mức tổn thất và số lần lặp lại. Hoàn tất quy trình này trong 6 lần lặp, chúng ta sẽ nhận được các trọng số, độ lệch và tổn thất sau:

Lần lặp lại	Trọng lượng	Thiên kiến	Tổn thất (MSE)
1	0	0	303,71
2	1,20	0,34	170,84
3	2,05	0,59	103,17
4	2,66	0,78	68,70
5	3,09	0,91	51,13
6	3,40	1,01	42,17

Bạn có thể thấy rằng mức tổn thất giảm xuống với mỗi trọng số và độ lệch được cập nhật. Trong ví dụ này, chúng ta dừng lại sau 6 lần lặp. Trên thực tế, một mô hình sẽ huấn luyện cho đến khi hội tụ. Khi một mô hình hội tụ, các lần lặp lại bổ sung sẽ không làm giảm tổn thất nữa vì phương pháp hạ độ dốc đã tìm thấy các trọng số và độ lệch gần như giảm thiểu tổn thất.

Nếu mô hình tiếp tục huấn luyện sau khi hội tụ, tổn thất sẽ bắt đầu dao động ở mức nhỏ khi mô hình liên tục cập nhật các tham số xung quanh các giá trị thấp nhất. Điều này có thể gây khó khăn cho việc xác minh rằng mô hình đã thực sự hội tụ. Để xác nhận rằng mô hình đã hội tụ, bạn nên tiếp tục huấn luyện cho đến khi tổn thất ổn định.

Đường cong hội tụ và đường cong tổn thất của mô hình

Khi huấn luyện một mô hình, bạn thường xem xét đường cong tổn thất để xác định xem mô hình có hội tụ hay không. Đường cong tổn thất cho biết mức tổn thất thay đổi như thế nào khi mô hình huấn luyện. Sau đây là hình dạng của một đường cong tổn thất điển hình. Mất mát trên trục y và các lần lặp lại trên trục x:

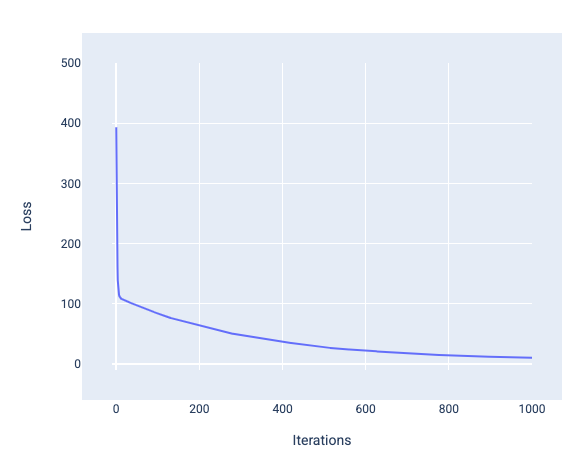
Hình 12 Đường cong tổn thất cho thấy mô hình hội tụ xung quanh dấu lặp lại thứ 1.000.

Bạn có thể thấy rằng mức tổn thất giảm đáng kể trong vài lần lặp lại đầu tiên, sau đó giảm dần trước khi ổn định ở khoảng lần lặp lại thứ 1.000. Sau 1.000 lần lặp lại, chúng ta có thể chắc chắn rằng mô hình đã hội tụ.

Trong các hình sau, chúng ta sẽ vẽ mô hình tại 3 điểm trong quá trình huấn luyện: điểm bắt đầu, điểm giữa và điểm kết thúc. Việc trực quan hoá trạng thái của mô hình tại các ảnh chụp nhanh trong quá trình huấn luyện sẽ củng cố mối liên kết giữa việc cập nhật trọng số và độ lệch, giảm tổn thất và hội tụ mô hình.

Trong các số liệu, chúng ta sử dụng các trọng số và độ lệch được suy ra tại một lần lặp cụ thể để biểu thị mô hình. Trong biểu đồ có các điểm dữ liệu và ảnh chụp nhanh mô hình, các đường tổn thất màu xanh dương từ mô hình đến các điểm dữ liệu cho biết mức tổn thất. Đường truyền càng dài thì tổn thất càng lớn.

Trong hình sau, chúng ta có thể thấy rằng vào khoảng lần lặp thứ hai, mô hình sẽ không dự đoán chính xác do mức tổn thất cao.

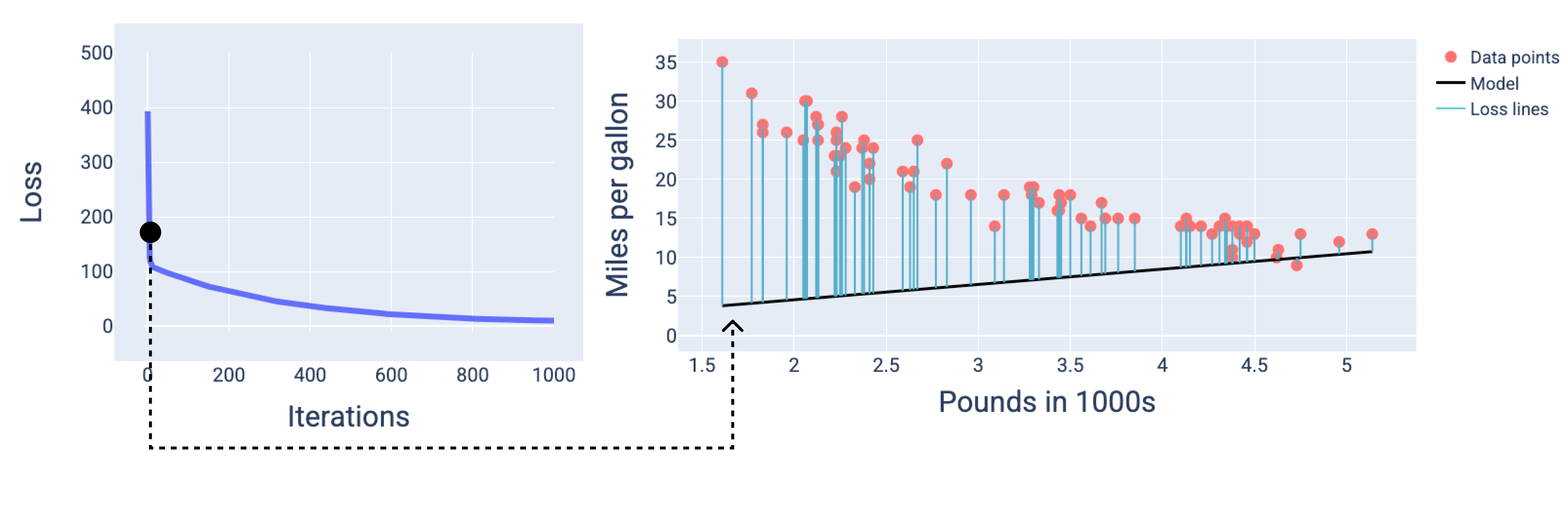
Hình 13. Đường cong tổn thất và ảnh chụp nhanh của mô hình khi bắt đầu quá trình huấn luyện.

Ở khoảng lần lặp thứ 400, chúng ta có thể thấy rằng phương pháp hạ độ dốc đã tìm ra trọng số và độ lệch tạo ra một mô hình tốt hơn.

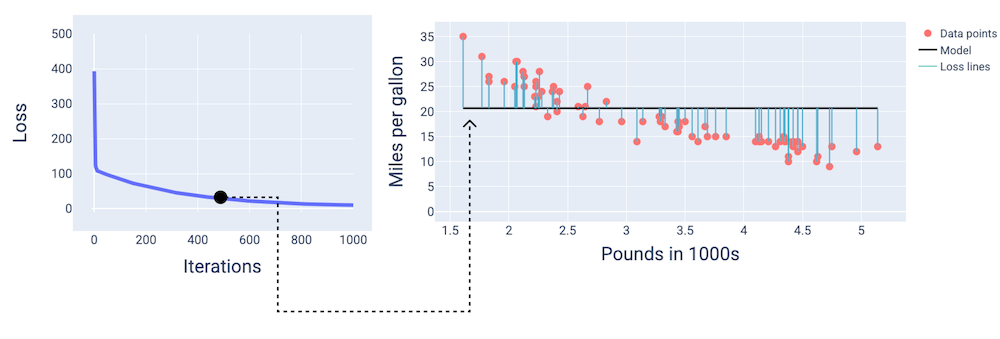
Hình 14. Đường cong tổn thất và ảnh chụp nhanh của mô hình vào khoảng giữa quá trình huấn luyện.

Và ở khoảng lần lặp thứ 1.000, chúng ta có thể thấy rằng mô hình đã hội tụ, tạo ra một mô hình có mức tổn thất thấp nhất có thể.

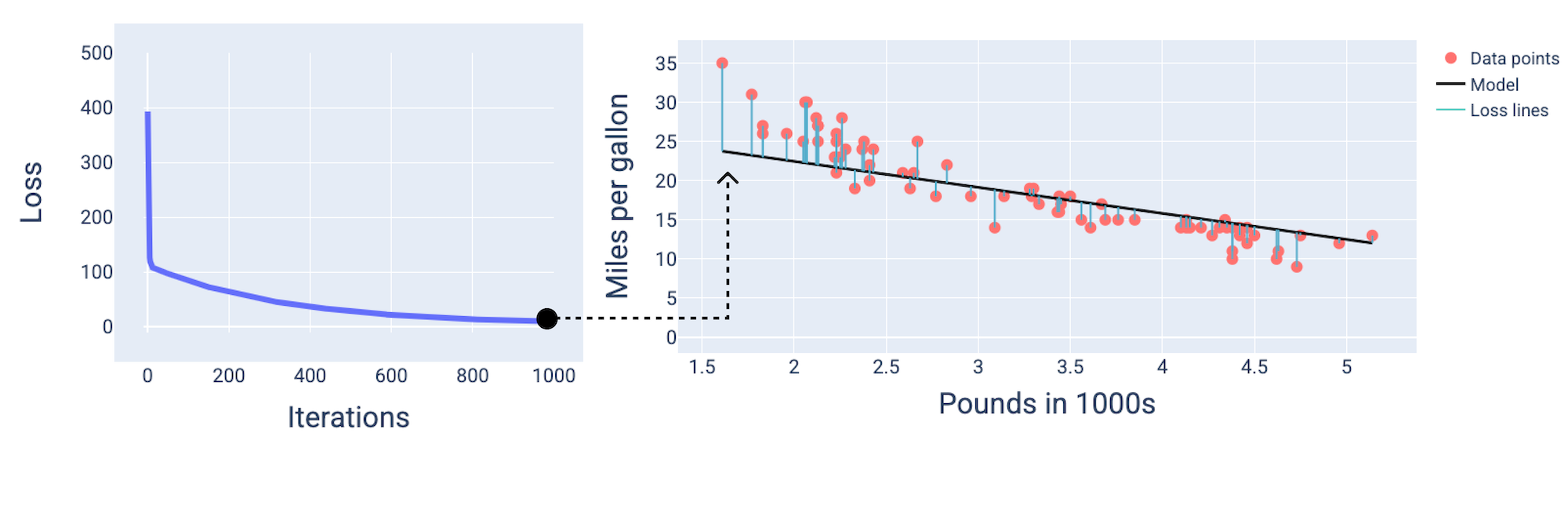
Hình 15. Đường cong tổn thất và ảnh chụp nhanh của mô hình gần cuối quy trình huấn luyện.

Bài tập: Kiểm tra mức độ hiểu biết của bạn

Vai trò của phương pháp hạ độ dốc trong hồi quy tuyến tính là gì?

Hạ dốc là một quy trình lặp đi lặp lại để tìm ra các trọng số và độ lệch tốt nhất nhằm giảm thiểu tổn thất.

Phương pháp hạ độ dốc giúp xác định loại tổn thất cần sử dụng khi huấn luyện một mô hình, ví dụ: L₁ hoặc L₂.

Phương pháp hạ độ dốc không liên quan đến việc chọn hàm tổn thất để huấn luyện mô hình.

Phương pháp hạ độ dốc loại bỏ các giá trị ngoại lệ khỏi tập dữ liệu để giúp mô hình đưa ra dự đoán chính xác hơn.

Phương pháp hạ độ dốc không làm thay đổi tập dữ liệu.

Hàm lồi và sự hội tụ

Các hàm tổn thất cho mô hình tuyến tính luôn tạo ra một bề mặt lồi. Do thuộc tính này, khi mô hình hồi quy tuyến tính hội tụ, chúng ta biết rằng mô hình đã tìm thấy các trọng số và độ lệch tạo ra mức tổn thất thấp nhất.

Nếu vẽ đồ thị bề mặt tổn thất cho một mô hình có một đặc điểm, chúng ta có thể thấy hình dạng lồi của mô hình đó. Sau đây là đường cong tổn thất cho một tập dữ liệu giả định về số dặm trên mỗi gallon. Trọng số nằm trên trục x, độ lệch nằm trên trục y và tổn thất nằm trên trục z:

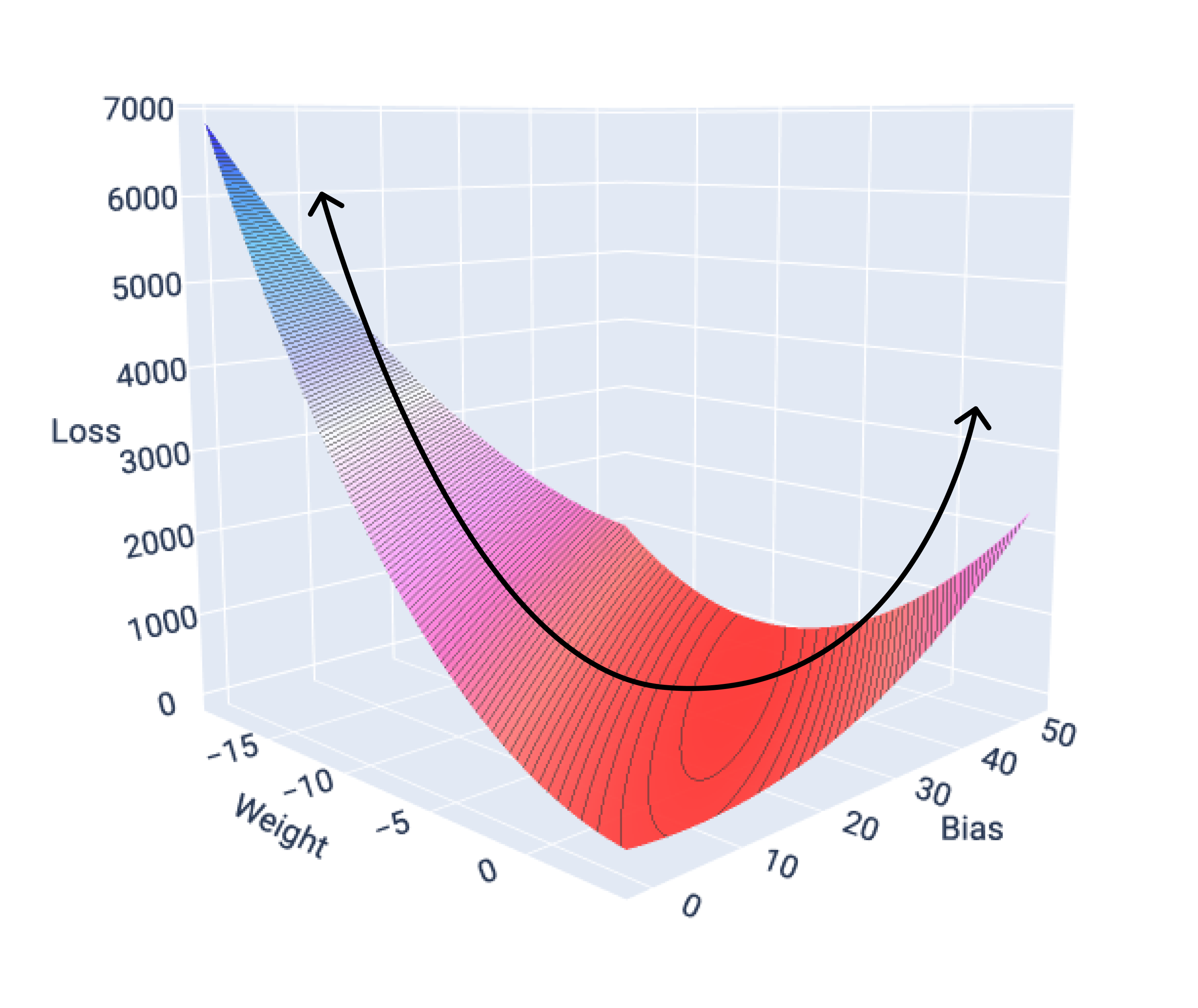
Hình 16. Mất bề mặt cho thấy hình dạng lồi của nó.

Trong ví dụ này, trọng số là -5,44 và độ lệch là 35,94 tạo ra mức tổn thất thấp nhất là 5,54:

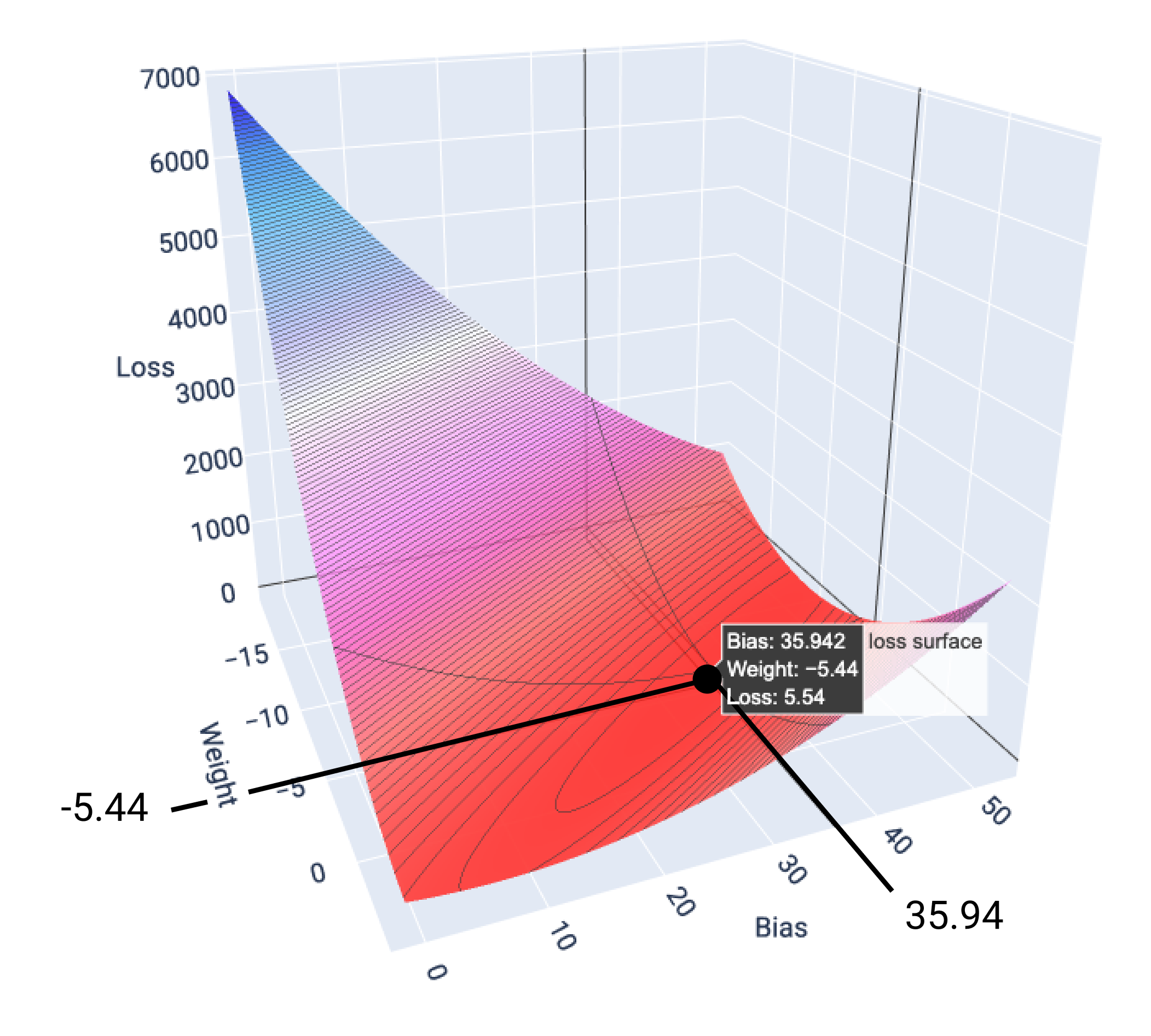
Hình 17. Mất bề mặt cho thấy các giá trị trọng số và độ lệch tạo ra mức tổn thất thấp nhất.

Một mô hình tuyến tính sẽ hội tụ khi tìm thấy mức tổn thất tối thiểu. Do đó, các lần lặp lại bổ sung chỉ khiến quá trình giảm độ dốc di chuyển các giá trị trọng số và độ lệch với số lượng rất nhỏ xung quanh mức tối thiểu. Nếu chúng ta vẽ đồ thị các điểm trọng số và độ lệch trong quá trình hạ độ dốc, thì các điểm sẽ trông giống như một quả bóng lăn xuống đồi, cuối cùng dừng lại ở điểm không còn độ dốc xuống.

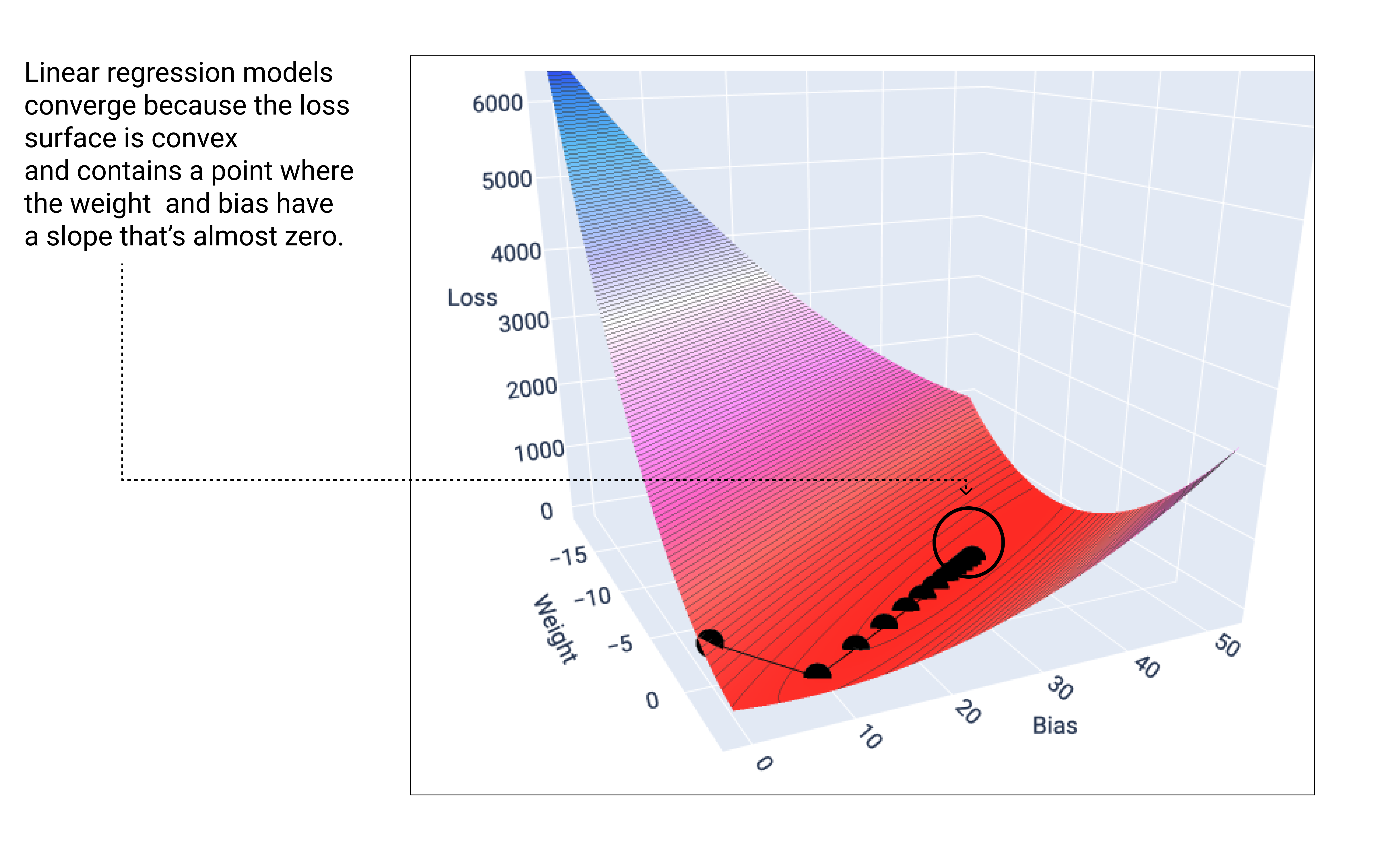
Hình 18. Biểu đồ tổn thất cho thấy các điểm hạ dốc dừng lại ở điểm thấp nhất trên biểu đồ.

Lưu ý rằng các điểm mất mát màu đen tạo ra hình dạng chính xác của đường cong mất mát: một đường giảm mạnh trước khi giảm dần cho đến khi đạt đến điểm thấp nhất trên bề mặt mất mát.

Điều quan trọng cần lưu ý là mô hình này hầu như không bao giờ tìm thấy giá trị tối thiểu chính xác cho từng trọng số và độ lệch, mà thay vào đó tìm thấy một giá trị rất gần với giá trị đó. Bạn cũng cần lưu ý rằng giá trị tối thiểu cho trọng số và độ lệch không tương ứng với mức tổn thất bằng 0, mà chỉ là giá trị tạo ra mức tổn thất thấp nhất cho tham số đó.

Khi sử dụng các giá trị trọng số và độ lệch tạo ra mức tổn thất thấp nhất (trong trường hợp này là trọng số -5,44 và độ lệch 35,94), chúng ta có thể vẽ biểu đồ mô hình để xem mức độ phù hợp của mô hình với dữ liệu:

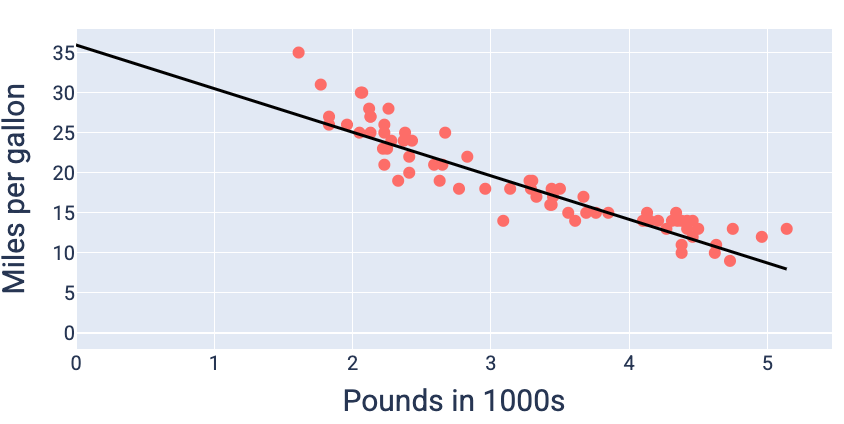
Hình 19. Mô hình được vẽ biểu đồ bằng cách sử dụng các giá trị trọng số và độ lệch tạo ra mức tổn thất thấp nhất.

Đây sẽ là mô hình tốt nhất cho tập dữ liệu này vì không có giá trị trọng số và độ lệch nào khác tạo ra mô hình có mức tổn thất thấp hơn.

Từ khoá:

• Convergence
• Hàm lồi
• Phương pháp giảm độ dốc
• Vòng lặp
• Đường cong tổn thất