النزول التدريجي هو أسلوب رياضي يحدّد بشكل متكرر الأوزان والانحيازات التي تؤدي إلى إنشاء نموذج بأقل خسارة. تجد طريقة "النزول التدريجي" أفضل وزن وانحياز من خلال تكرار العملية التالية لعدد من التكرارات التي يحدّدها المستخدم.
يبدأ النموذج التدريب بأوزان وتحيزات عشوائية قريبة من الصفر، ثم يكرّر الخطوات التالية:
احسب مقدار الخسارة باستخدام الوزن والانحياز الحاليين.
تحديد اتجاه نقل الأوزان والانحياز الذي يقلّل من الخسارة
نقل قيم الوزن والانحياز بمقدار صغير في الاتجاه الذي يقلل من الخسارة
ارجع إلى الخطوة الأولى وكرِّر العملية إلى أن يتعذّر على النموذج تقليل الخسارة أكثر من ذلك.
يوضّح الرسم البياني أدناه الخطوات التكرارية التي تنفّذها عملية "النزول التدريجي" للعثور على الأوزان والانحياز اللذين ينتجان النموذج بأقل خسارة.
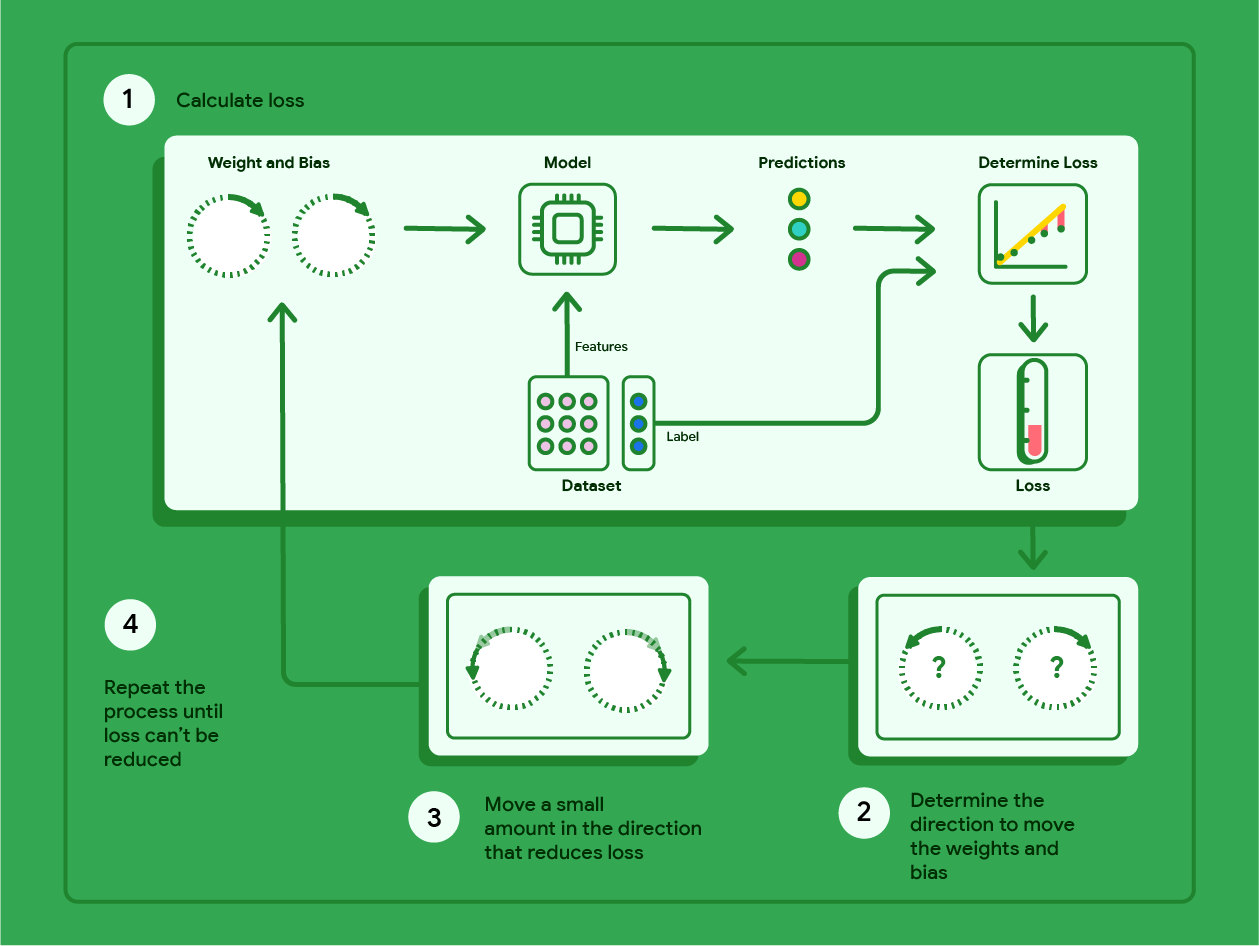
الشكل 11 الانحدار التدريجي هو عملية تكرارية تحدّد الأوزان والانحياز اللذين ينتج عنهما النموذج الذي يحقّق أقل خسارة.
انقر على رمز الإضافة لمعرفة المزيد عن العمليات الحسابية التي تستند إليها طريقة "النزول التدريجي".
على مستوى ملموس، يمكننا استعراض خطوات نزول التدرّج باستخدام مجموعة بيانات صغيرة تتضمّن سبعة أمثلة على وزن السيارة بالرطل ومعدّل استهلاكها للوقود بالكيلومترات لكل غالون:
| الجنيهات بالآلاف (ميزة) | ميل لكل غالون (التصنيف) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- يبدأ النموذج التدريب من خلال ضبط الوزن والانحياز على صفر:
- احسب خسارة متوسط الخطأ المربع باستخدام مَعلمات النموذج الحالي:
- احتساب ميل المماس لدالة الخسارة عند كل وزن والتحيز:
- حرِّك مقدارًا صغيرًا في اتجاه الميل السالب للحصول على الوزن والانحياز التاليَين. في الوقت الحالي، سنعرّف بشكل عشوائي "المبلغ الصغير" على أنّه 0.01:
انقر على رمز الإضافة للتعرّف على كيفية حساب الميل.
للحصول على ميل الخطوط المماسّة للوزن والانحياز، نحسب مشتقة دالة الخسارة بالنسبة إلى الوزن والانحياز، ثم نحل المعادلات.
سنكتب معادلة إجراء التوقّعات على النحو التالي:
$ f_{w,b}(x) = (w*x)+b $.
سنكتب القيمة الفعلية على النحو التالي: $ y $.
سنحتسب متوسط الخطأ التربيعي باستخدام المعادلة التالية:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
حيث يمثّل $i$ المثال التدريبي رقم $i$ ويمثّل $M$ عدد الأمثلة.
يمكن كتابة مشتقة دالة الخسارة بالنسبة إلى الوزن على النحو التالي:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
وتكون قيمتها:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
نجمع أولاً كل قيمة متوقّعة مطروحًا منها القيمة الفعلية، ثم نضرب الناتج في ضعف قيمة السمة. بعد ذلك، نقسّم المجموع على عدد الأمثلة. والنتيجة هي ميل الخط المماس لقيمة الوزن.
إذا حللنا هذه المعادلة باستخدام وزن وانحياز يساويان صفرًا، سنحصل على -119.7 لميل الخط.
مشتقة الانحياز
يمكن كتابة مشتق دالة الخسارة بالنسبة إلى الانحياز على النحو التالي:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
وتكون النتيجة:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
أولاً، نجمع كل قيمة متوقّعة مطروحًا منها القيمة الفعلية، ثم نضرب الناتج في اثنين. ثم نقسم المجموع على عدد الأمثلة. والنتيجة هي ميل الخط المماس لقيمة الانحياز.
إذا حللنا هذه المعادلة باستخدام وزن وانحياز يساويان صفرًا، سنحصل على -34.3 لميل الخط.
استخدِم الوزن والانحياز الجديدَين لاحتساب الخسارة وكرِّر العملية. بعد إكمال العملية لست مرات، سنحصل على الأوزان والانحيازات والخسائر التالية:
| التكرار | الوزن | الانحياز | الخسارة (الخطأ التربيعي المتوسّط) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
يمكنك ملاحظة أنّ الخسارة تنخفض مع كل وزن وانحياز معدَّلَين. في هذا المثال، توقّفنا بعد ست تكرارات. من الناحية العملية، يتم تدريب النموذج إلى أن يتقارب. عندما يتقارب النموذج، لا تؤدي التكرارات الإضافية إلى تقليل الخسارة بشكل أكبر لأنّ عملية "النزول التدريجي" قد عثرت على الأوزان والانحياز اللذين يقلّلان الخسارة إلى أدنى حدّ.
إذا استمرّ النموذج في التدريب بعد التقارب، سيبدأ معدّل الخطأ في التقلّب بكميات صغيرة لأنّ النموذج يواصل تعديل المَعلمات حول أدنى قيمها. ويمكن أن يصعّب ذلك التحقّق من أنّ النموذج قد تقارب بالفعل. للتأكّد من أنّ النموذج قد تقارب، عليك مواصلة التدريب إلى أن يستقر معدّل الخطأ.
تقارب النماذج ومنحنيات الخسارة
عند تدريب نموذج، ستنظر غالبًا إلى منحنى الخسارة لتحديد ما إذا كان النموذج قد تقارب. يعرض منحنى الخسارة كيفية تغيُّر الخسارة أثناء تدريب النموذج. في ما يلي شكل منحنى الخسارة النموذجي. يظهر معدّل الخطأ على المحور الصادي والتكرارات على المحور السيني:
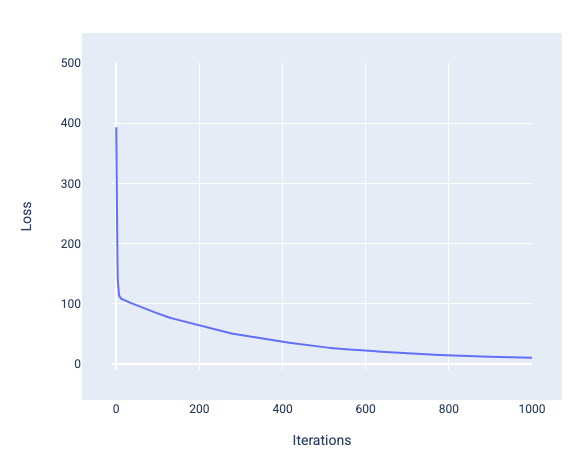
الشكل 12 منحنى الخسارة الذي يعرض النموذج الذي يتقارب حول علامة التكرار الألف.
يمكنك ملاحظة أنّ الخسارة تنخفض بشكل كبير خلال التكرارات القليلة الأولى، ثم تنخفض تدريجيًا قبل أن تستقر عند التكرار رقم 1,000 تقريبًا. بعد 1,000 تكرار، يمكننا التأكّد إلى حد كبير من أنّ النموذج قد تقارب.
في الأشكال التالية، نرسم النموذج في ثلاث نقاط خلال عملية التدريب: البداية والمنتصف والنهاية. يؤدي عرض حالة النموذج بشكل مرئي في لقطات أثناء عملية التدريب إلى تعزيز العلاقة بين تعديل الأوزان والتحيّز وتقليل الخسارة وتقارب النموذج.
في الأشكال، نستخدم الأوزان والانحياز المشتقَّين في تكرار معيّن لتمثيل النموذج. في الرسم البياني الذي يتضمّن نقاط البيانات ولقطة النموذج، تعرض خطوط الفقدان الزرقاء من النموذج إلى نقاط البيانات مقدار الفقدان. وكلما طالت الخطوط، زادت الخسارة.
في الشكل التالي، نلاحظ أنّه في التكرار الثاني تقريبًا، لن يكون النموذج جيدًا في تقديم التوقعات بسبب ارتفاع مقدار الخطأ.
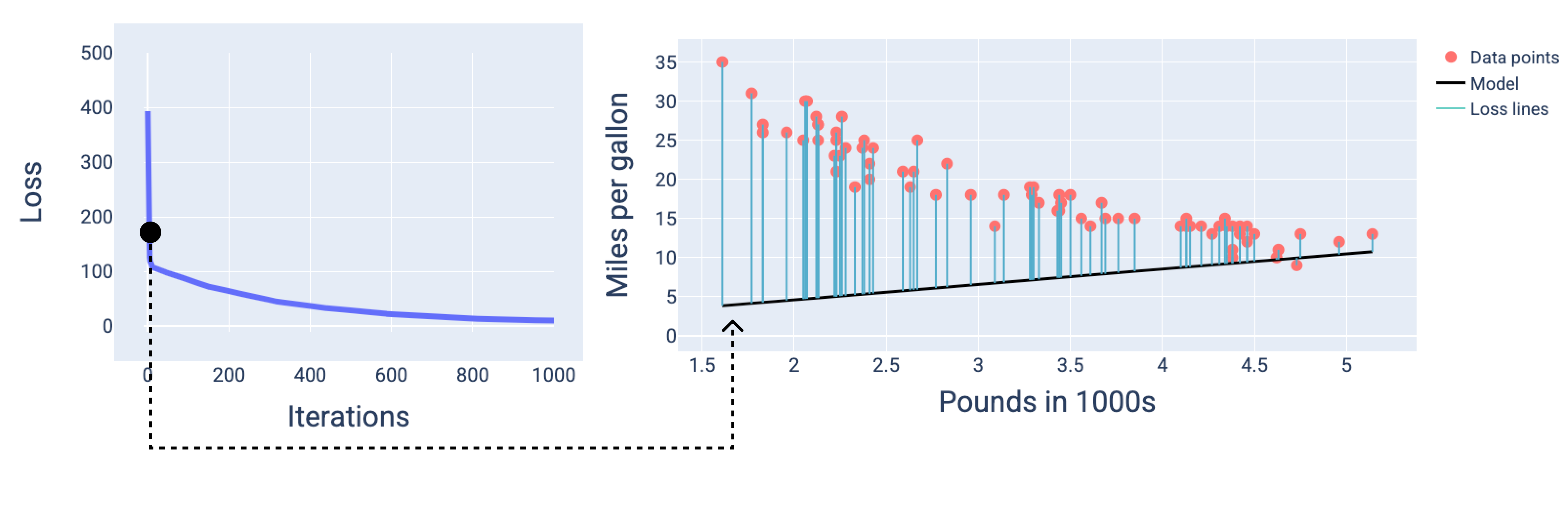
الشكل 13 رسم بياني لفقدان البيانات ولقطة للشكل في بداية عملية التدريب
في التكرار رقم 400 تقريبًا، نلاحظ أنّ طريقة "النزول التدريجي" قد عثرت على الوزن والانحياز اللذين ينتجان نموذجًا أفضل.
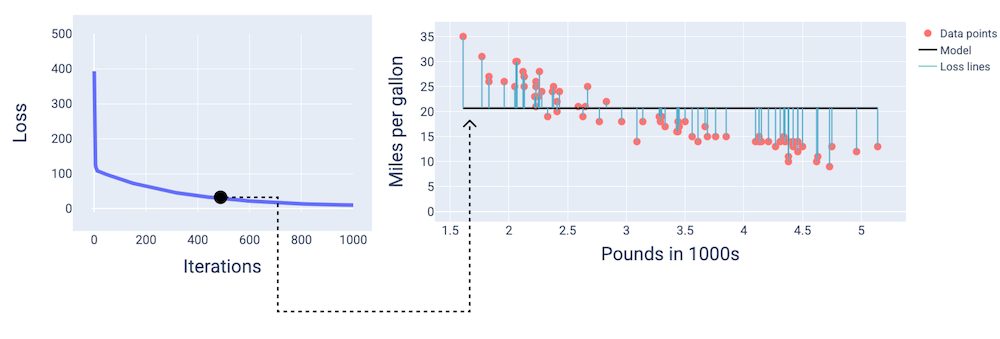
الشكل 14 منحنى الخسارة ولقطة للنموذج في منتصف عملية التدريب تقريبًا
وبعد حوالي 1,000 تكرار، نلاحظ أنّ النموذج قد تقارب، ما أدّى إلى إنشاء نموذج بأقل خسارة ممكنة.
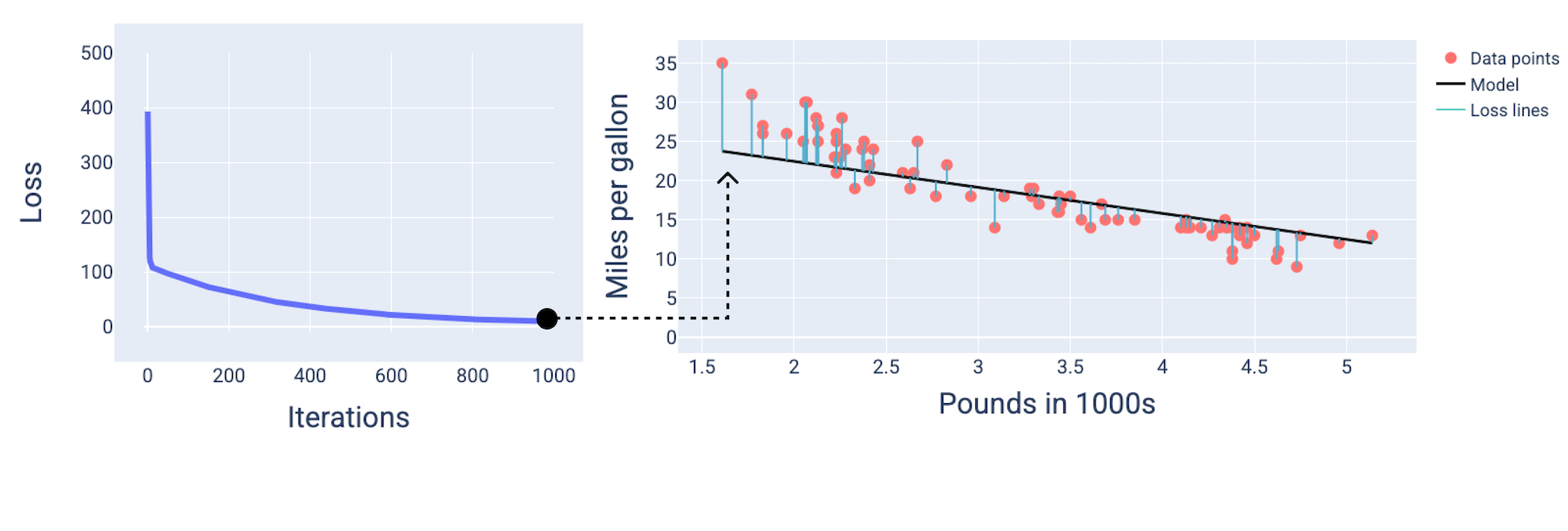
الشكل 15 منحنى الخسارة ولقطة للنموذج بالقرب من نهاية عملية التدريب
تمرين: التحقّق من فهمك
التقارب والدوال المحدّبة
تنتج دوال الخسارة للنماذج الخطية دائمًا سطحًا محدبًا. نتيجةً لهذه السمة، عندما يتقارب نموذج الانحدار الخطي، نعلم أنّ النموذج قد عثر على الأوزان والانحياز اللذين يؤديان إلى أقل خسارة.
إذا رسمنا بيانيًا سطح دالة الخسارة لنموذج يتضمّن ميزة واحدة، يمكننا ملاحظة شكله المحدّب. في ما يلي سطح الخسارة لمجموعة بيانات افتراضية حول عدد الأميال المقطوعة لكل غالون. الوزن على المحور السيني، والانحياز على المحور الصادي، والخسارة على المحور العيني:
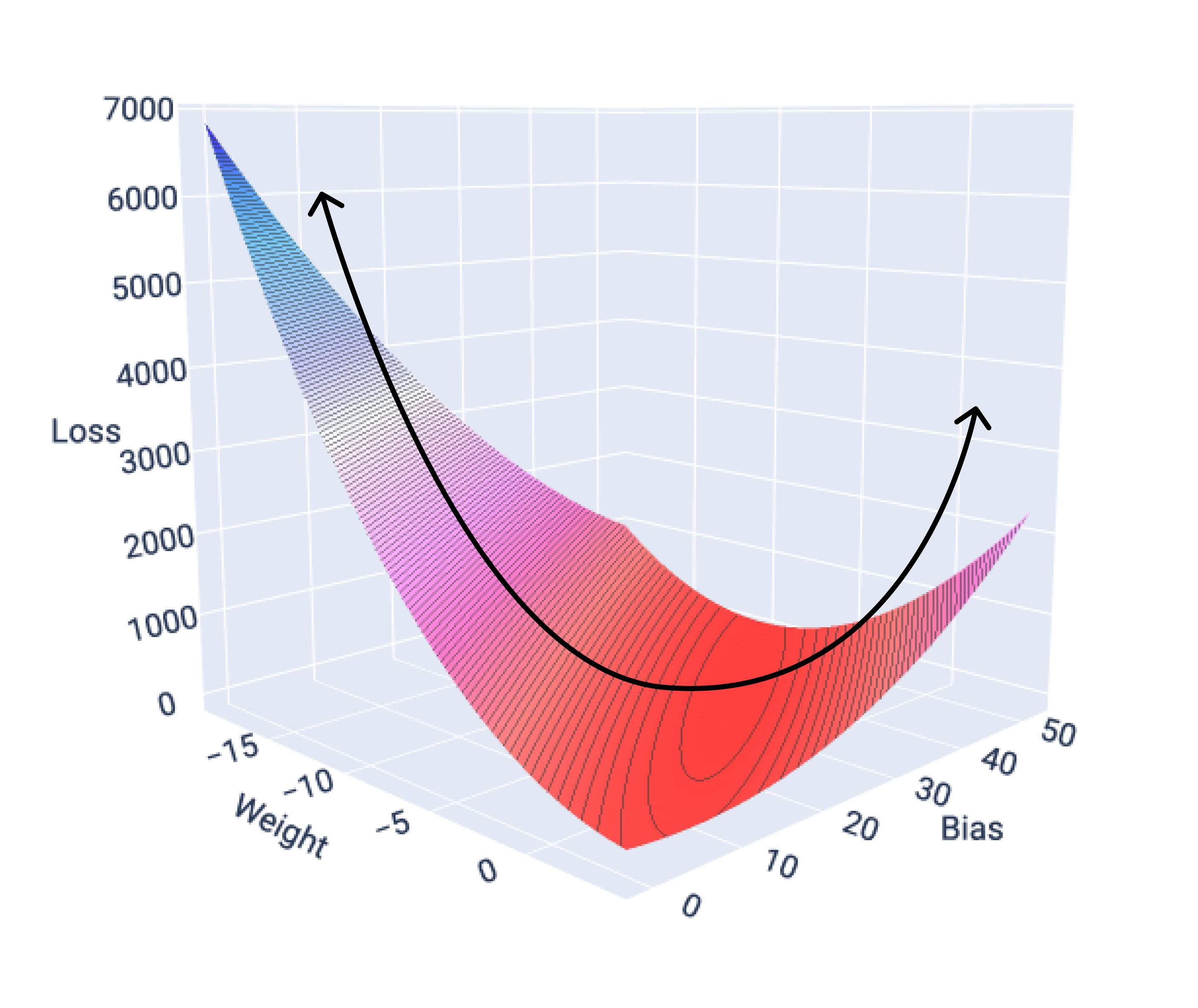
الشكل 16. سطح الخسارة الذي يعرض شكله المحدّب
في هذا المثال، يؤدي التقدير -5.44 والانحياز 35.94 إلى أقل خسارة عند 5.54:
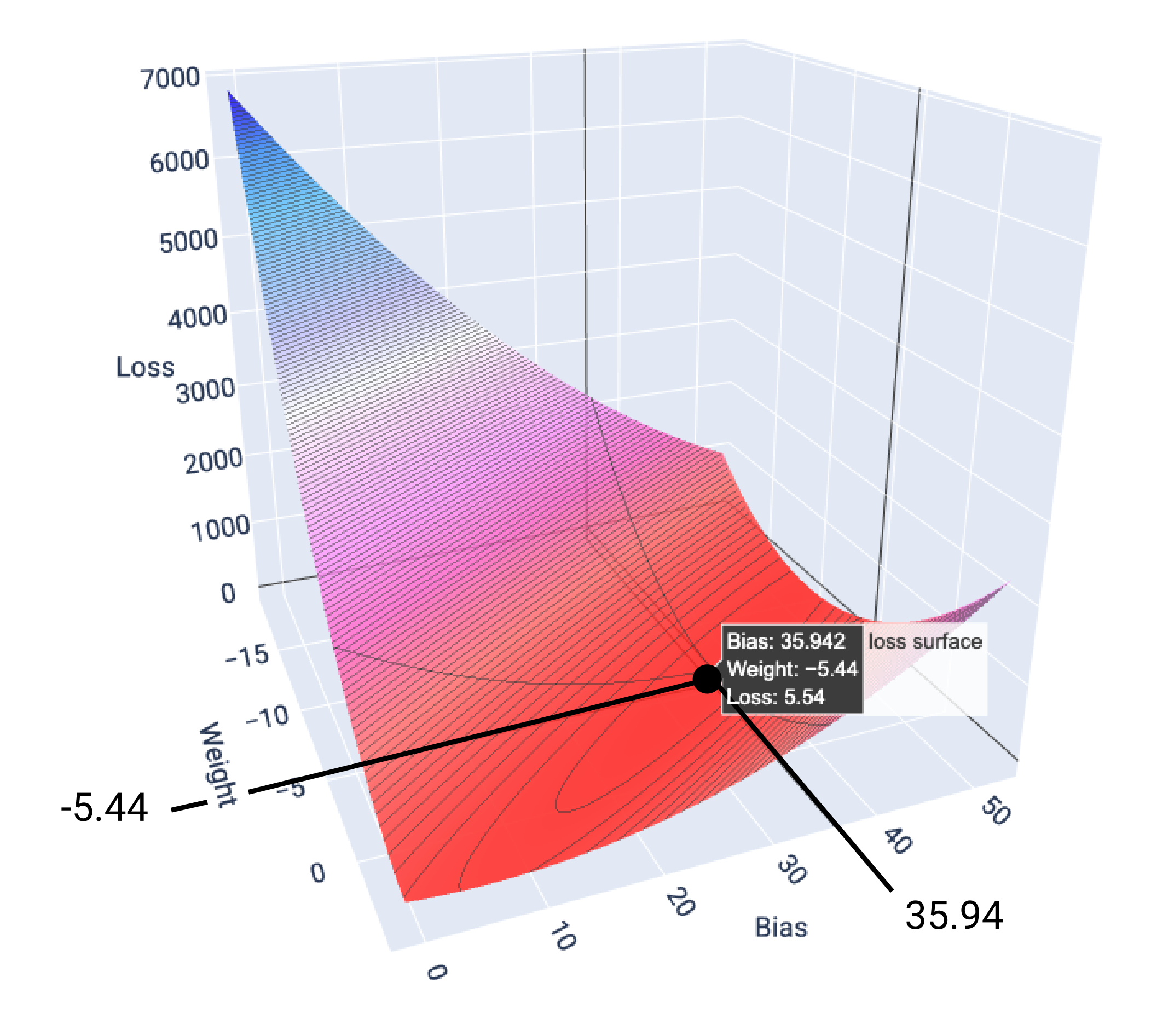
الشكل 17 رسم بياني لسطح الدالة الهدف يعرض قيم الأوزان والانحياز التي تؤدي إلى أقل خسارة
يتقارب النموذج الخطي عندما يعثر على الحد الأدنى من الخسارة. لذلك، لا تؤدي التكرارات الإضافية إلا إلى تحريك قيم الوزن والانحياز بمقادير صغيرة جدًا حول الحد الأدنى. إذا رسمنا بيانيًا نقاط الأوزان والانحياز أثناء عملية نزول التدرّج، ستبدو النقاط وكأنّها كرة تتدحرج نزولاً من تل، وتتوقف أخيرًا عند النقطة التي لا يوجد فيها المزيد من المنحدرات.
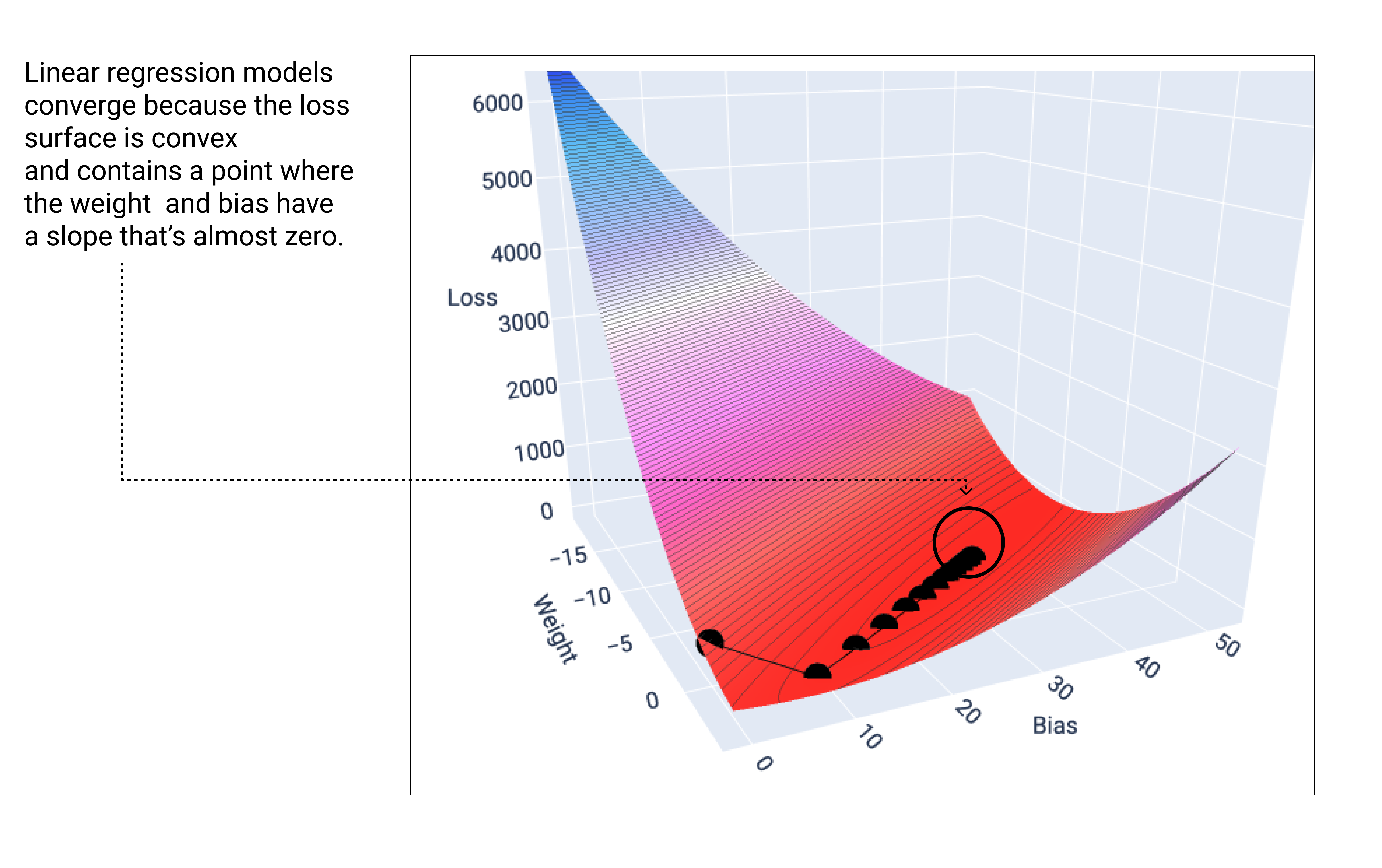
الشكل 18 رسم بياني للخسارة يعرض نقاط انحدار متدرّج تتوقف عند أدنى نقطة في الرسم البياني
لاحظ أنّ نقاط الخسارة السوداء تشكّل الشكل الدقيق لمنحنى الخسارة: انخفاض حاد قبل أن ينحدر تدريجيًا إلى أن يصل إلى أدنى نقطة على سطح الخسارة.
من المهم ملاحظة أنّ النموذج لا يعثر أبدًا على الحد الأدنى الدقيق لكل وزن وانحياز، بل يعثر على قيمة قريبة جدًا منه. من المهم أيضًا ملاحظة أنّ الحد الأدنى للأوزان والانحياز لا يتوافق مع فقدان البيانات، بل مع قيمة تؤدي إلى أقل قدر من فقدان البيانات لتلك المَعلمة.
باستخدام قيم الوزن والانحياز التي تؤدي إلى أقل خسارة، وهي في هذه الحالة وزن يبلغ -5.44 وانحياز يبلغ 35.94، يمكننا رسم النموذج بيانيًا لمعرفة مدى ملاءمته للبيانات:
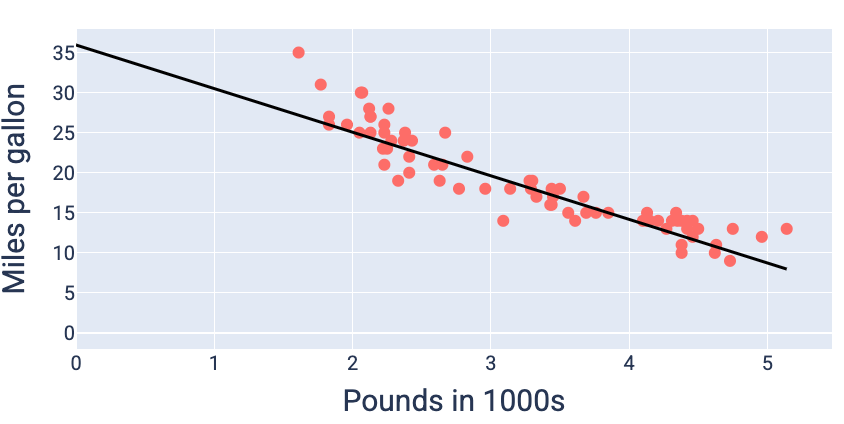
الشكل 19. النموذج الذي تم رسمه بيانيًا باستخدام قيم الوزن والانحياز التي تؤدي إلى أقل خسارة
سيكون هذا هو النموذج الأفضل لمجموعة البيانات هذه لأنّه لا توجد قيم أخرى للأوزان والانحياز تنتج نموذجًا بخسارة أقل.
