Градієнтний спуск – це математичний метод, що ітераційно знаходить значення ваги й зсуву, які дають змогу створити модель із найменшими втратами. Градієнтний спуск знаходить найкращі значення ваги й зсуву, повторюючи процес, описаний нижче, протягом кількох ітерацій, які визначає користувач.
Модель починає навчання з рандомізованими значеннями ваги й зсуву, близькими до нуля, а потім повторює такі кроки:
Обчислення втрат із поточною вагою і зсувом.
Визначення напрямку, у якому переміщувати значення ваги й зсуву, що зменшують втрати.
Незначне переміщення значень ваги й зсуву в напрямку, що зменшує втрати.
Повернення до першого кроку й повторення процесу, доки модель не зможе більше зменшувати втрати.
На діаграмі нижче показано ітераційні кроки градієнтного спуску, які виконуються для визначення значень ваги й зсуву, що дають змогу створити модель із найменшими втратами.
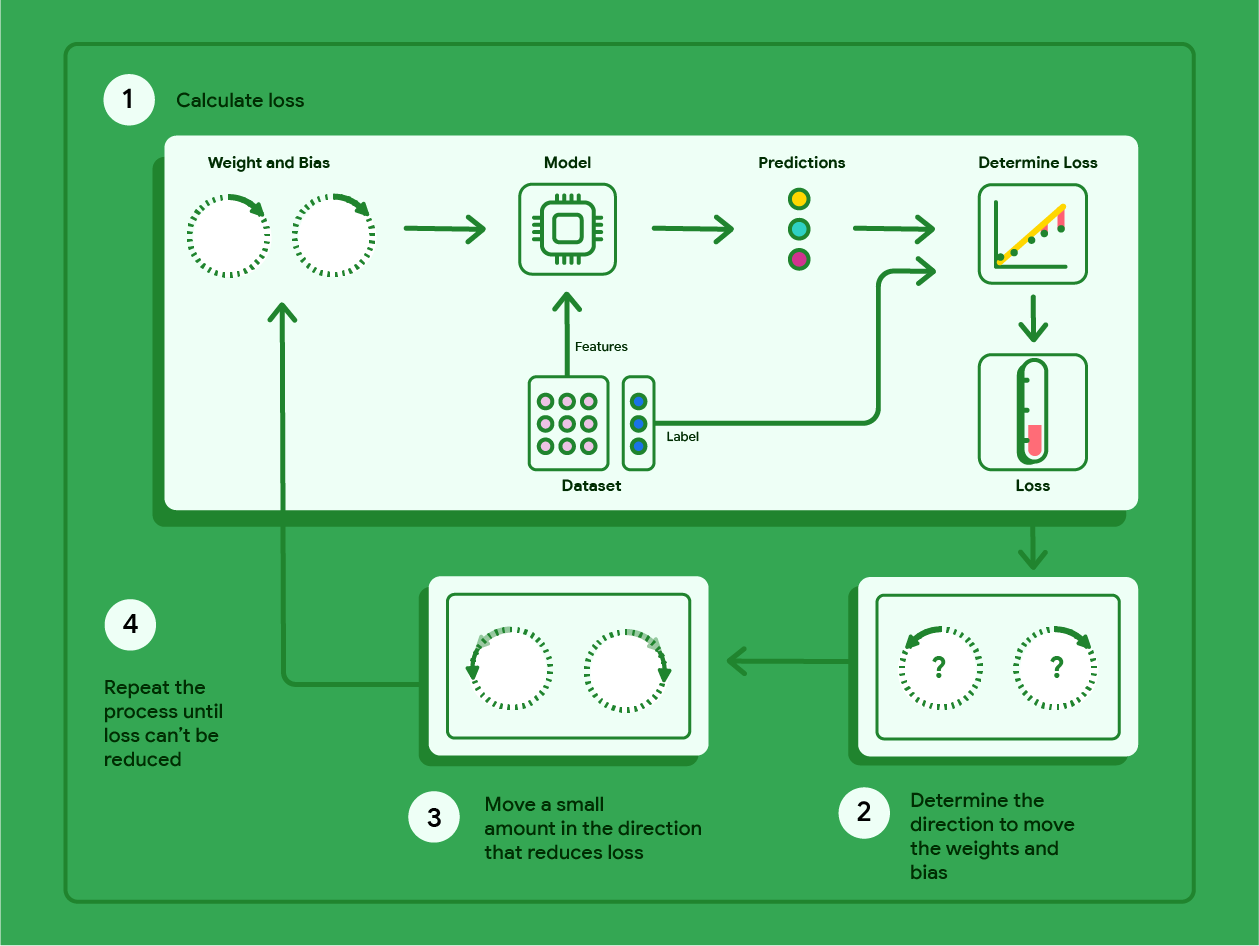
Рисунок 12. Градієнтний спуск – це ітераційний процес пошуку значень ваги й зсуву, що дають змогу створити модель із найменшими втратами.
Натисніть значок плюса, щоб дізнатися більше про математичне підґрунтя градієнтного спуску.
На конкретному рівні ми можемо пройти кроки градієнтного спуску, використовуючи невеликий набір даних, який містить сім прикладів із вагою автомобіля у фунтах і витратою палива в милях на галон.
| Фунти в тисячах (ознака) | Милі на галон (мітка) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
- Модель починає навчання, встановлюючи нуль як значення ваги й зсуву:
- Слід обчислити втрати MSE з поточними параметрами моделі:
- Слід обчислити нахил дотичної до функції втрат для кожного значення ваги й зсуву:
- Виконайте незначне переміщення в напрямку негативного нахилу, щоб отримати значення ваги й зсуву, наведені нижче. Для цього прикладу ми довільно визначимо "незначне" як 0,01.
Натисніть значок плюса, щоб дізнатися, як обчислювати нахил.
Щоб отримати нахил ліній, дотичних до значень ваги й зсуву, ми беремо похідну функції втрат відносно цих значень, а потім розв’язуємо рівняння.
Потрібно записати рівняння для прогнозування так:
$ f_{w,b}(x) = (w*x)+b $.
Слід записати фактичне значення так: $ y $.
Ми розрахуємо MSE, використовуючи цю формулу:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
У ній $i$ – це навчальний приклад $ith$, а $M$ – кількість прикладів.
Похідна функції втрат відносно значення ваги записується так:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
Вона дорівнює:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
Спочатку слід додати різницю кожного прогнозного й фактичного значення, а потім помножити суму на подвоєне значення ознаки. Потім слід поділити суму на кількість прикладів. Результатом є кут нахилу лінії, дотичної до значення ваги.
Якщо в рівнянні значення ваги й зсуву дорівнюють нулю, ми отримаємо число –119,7 для нахилу лінії.
Похідна значення зсуву
Похідна функції втрат відносно значення зсуву записується так:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
Вона дорівнює:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
Спочатку слід додати різницю кожного прогнозного й фактичного значення, а потім помножити суму на два. Потім слід поділити суму на кількість прикладів. Результатом є кут нахилу лінії, дотичної до значення зсуву.
Якщо в рівнянні значення ваги й зсуву дорівнюють нулю, ми отримаємо число –34,3 для нахилу лінії.
Використовуйте нові значення ваги й зсуву, щоб розрахувати втрати, і повторіть кроки. Виконавши шість ітерацій цього процесу, ми отримаємо такі значення ваги, зсуву й втрат:
| Ітерація | Вага | Зсув | Втрати (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303,71 |
| 2 | 1,2 | 0,34 | 170,67 |
| 3 | 2,75 | 0,59 | 67,3 |
| 4 | 3,17 | 0,72 | 50,63 |
| 5 | 3,47 | 0,82 | 42,1 |
| 6 | 3,68 | 0,9 | 37,74 |
Ви бачите, що втрати стають меншими з кожним оновленням значень ваги й зсуву. У цьому прикладі ми зупинилися після шести ітерацій. На практиці модель навчається, доки не досягне збіжності. Коли досягнуто збіжності моделі, додаткові ітерації не зменшують втрати ще більше, оскільки градієнтний спуск знайшов значення ваги й зсуву, які зводять втрати майже до мінімуму.
Якщо модель продовжує навчатися після збіжності, втрати починають дещо коливатися, оскільки модель постійно оновлює параметри, які стосуються їх найнижчих значень. Через це може бути складно перевірити, що модель дійсно досягла збіжності. Щоб переконатися, що модель досягла збіжності, потрібно продовжити навчання, доки рівень втрат не стабілізується.
Криві збіжності й втрат моделі
Навчаючи модель, ви часто дивитиметеся на криву втрат, щоб визначити, чи вона досягла збіжності. Крива втрат показує, як втрати змінюються під час навчання моделі. На рисунку нижче зображено, як виглядає типова крива втрат. За втрати відповідає вісь Y, а за ітерації – X:
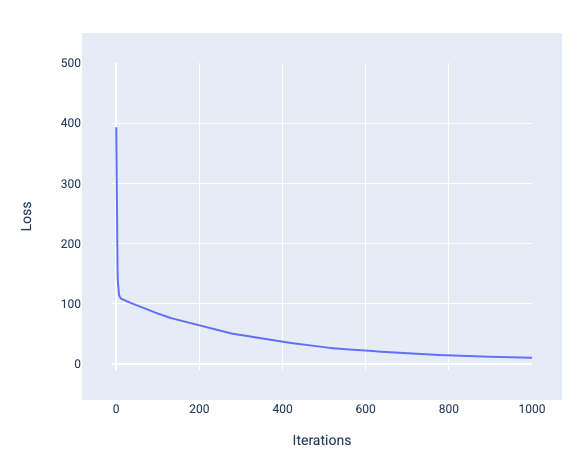
Рисунок 13. Крива втрат, яка показує, що модель досягає збіжності біля позначки 1000-ї ітерації.
Як можна побачити, втрати різко падають протягом перших кількох ітерацій, а потім зменшуються поступово, перш ніж вирівнятися під час 1000-ї ітерації. Можна стверджувати майже напевно, що модель досягла збіжності після 1000 ітерацій.
На наступних рисунках зображено стан моделі в трьох точках навчання: на його початку, у середині й кінці. Візуалізація моделі на знімках стану під час навчання переконливо демонструє зв’язок між оновленнями значень ваги й зсуву, зменшенням втрат і збіжністю.
Щоб показати модель на рисунках, використовуються отримані значення ваги й зсуву конкретних ітерацій. На графіку з точками даних і знімком стану моделі сині лінії втрат, проведені від моделі до точок даних, показують суму втрат. Що довші лінії, то більше втрат.
З наступного рисунка видно, що приблизно після другої ітерації модель ще не зможе робити хороші прогнози через велику кількість втрат.
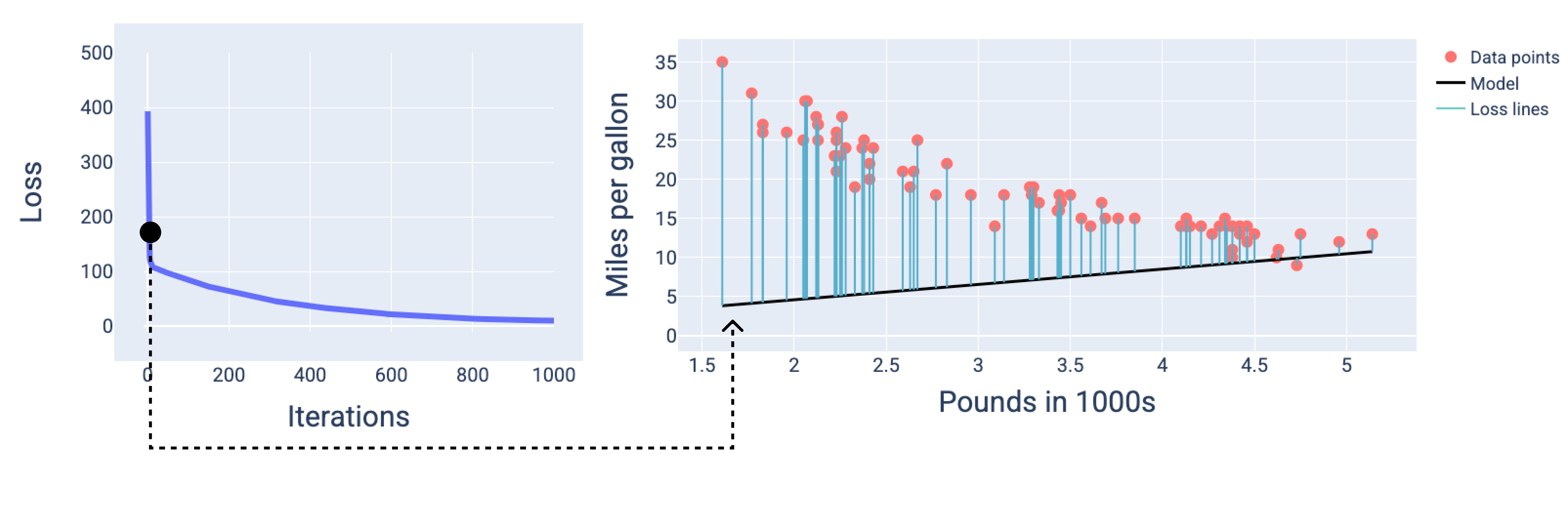
Рисунок 14. Крива втрат і знімок стану моделі на початку навчання.
Видно, що приблизно на 400-й ітерації градієнтний спуск знайшов значення ваги й зсуву, які покращили модель.
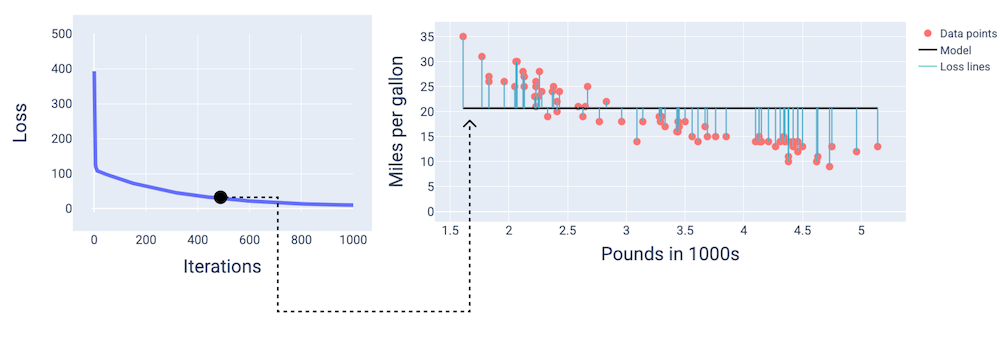
Рисунок 15. Крива втрат і знімок стану моделі приблизно в середині навчання.
Видно, що приблизно на 1000-й ітерації модель досягла збіжності й, як наслідок, має найменший можливий рівень втрат.
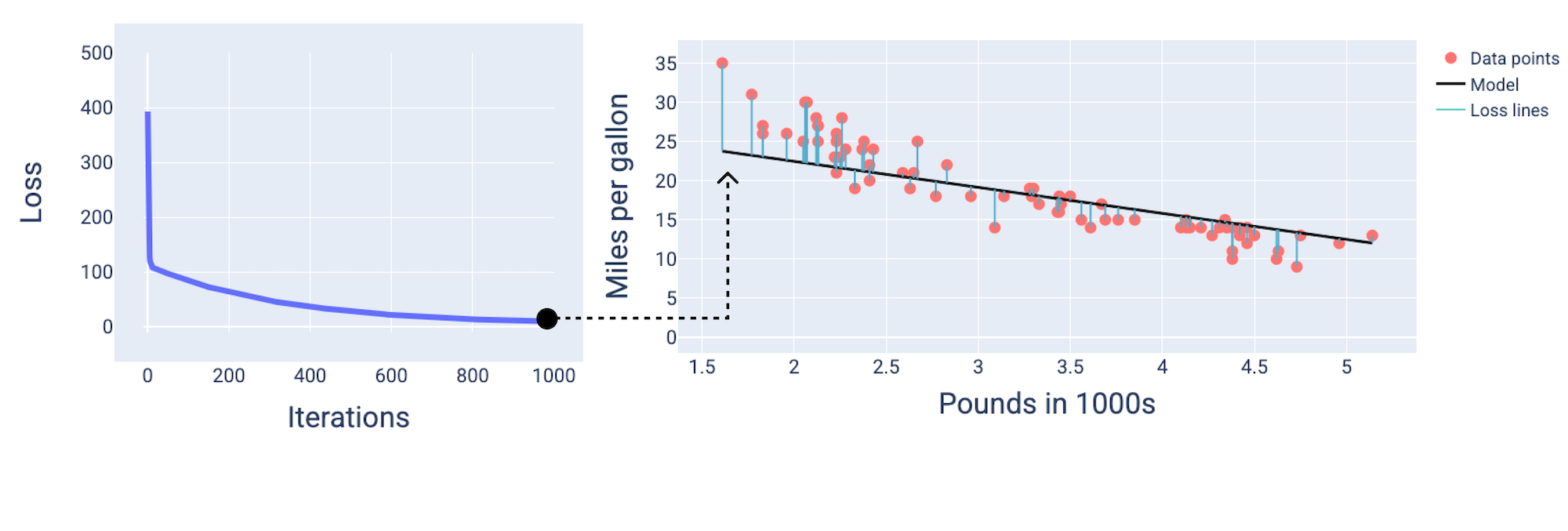
Рисунок 16. Крива втрат і знімок стану моделі під кінець навчання.
Вправа. Перевірте свої знання
Збіжність і опукла функція
Функції втрат для лінійних моделей завжди утворюють опуклу поверхню. Завдяки цій властивості ми знаємо, що досягнення збіжності свідчить про те, що модель лінійної регресії знайшла значення ваги й зсуву, які призводять до найменших втрат.
Якщо зобразити поверхню втрат для моделі з однією ознакою, буде видно її опуклу форму. Нижче показано поверхню втрати для набору даних із мітками "Милі на галон", використаного в попередніх прикладах. За вагу відповідає вісь X, за зсув – Y, а за втрати – Z.
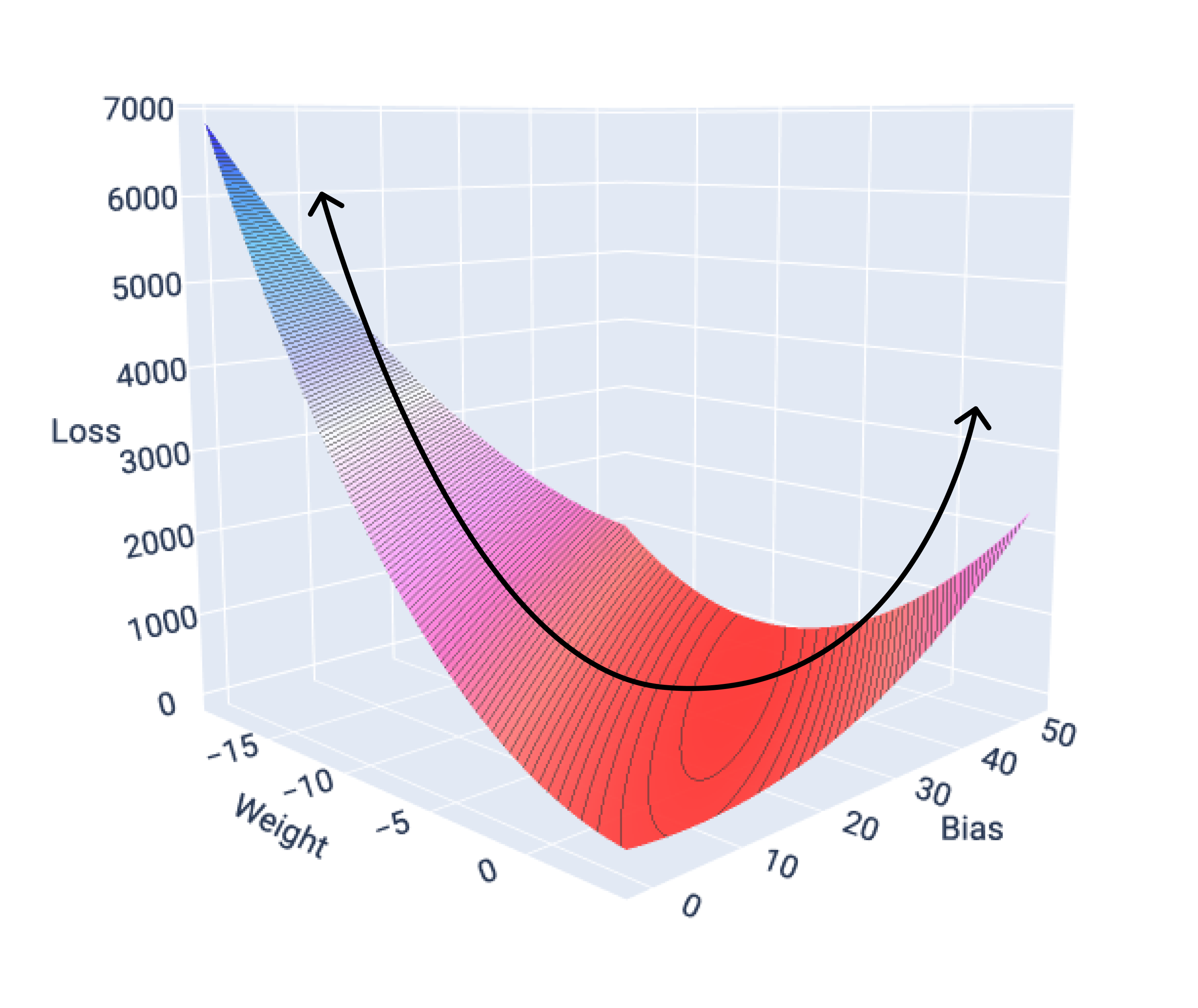
Рисунок 17. Поверхня втрат опуклої форми.
У цьому прикладі вага –5,44 і зсув 35,94 дають найменші втрати (5,54):
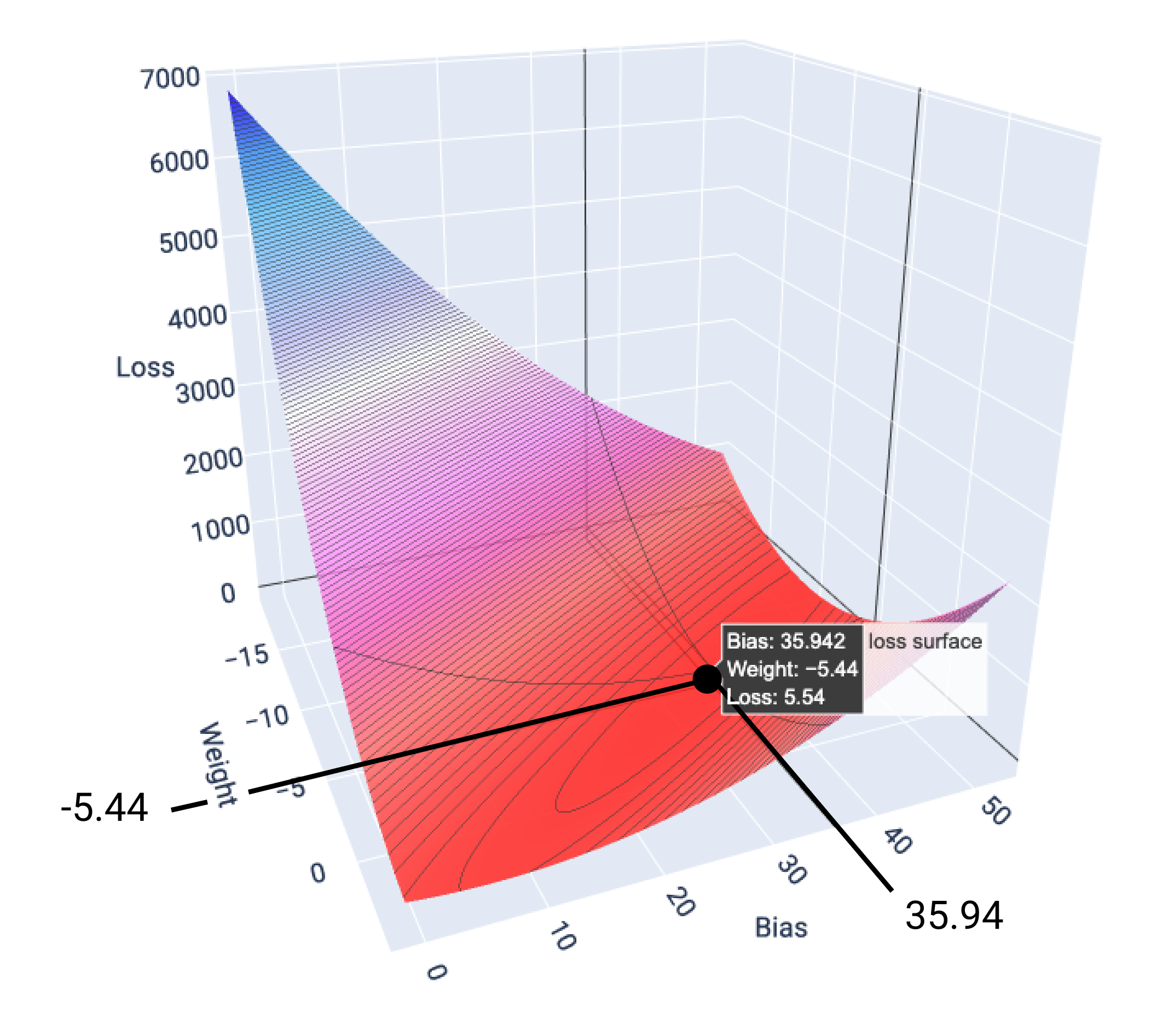
Рисунок 18. Поверхня втрат зі значеннями ваги й зсуву, які дають найменші втрати.
Лінійна модель збігається, коли досягає якнайменшого рівня втрат. Тому під час додаткових ітерацій градієнтний спуск лише трохи змінює мінімальні значення ваги й зсуву. Якщо побудувати графік, що показує поведінку точок ваги й зсуву під час градієнтного спуску, вони виглядали б як м’яч, що котиться з пагорба й зупиняється в місці, де більше немає схилу вниз.
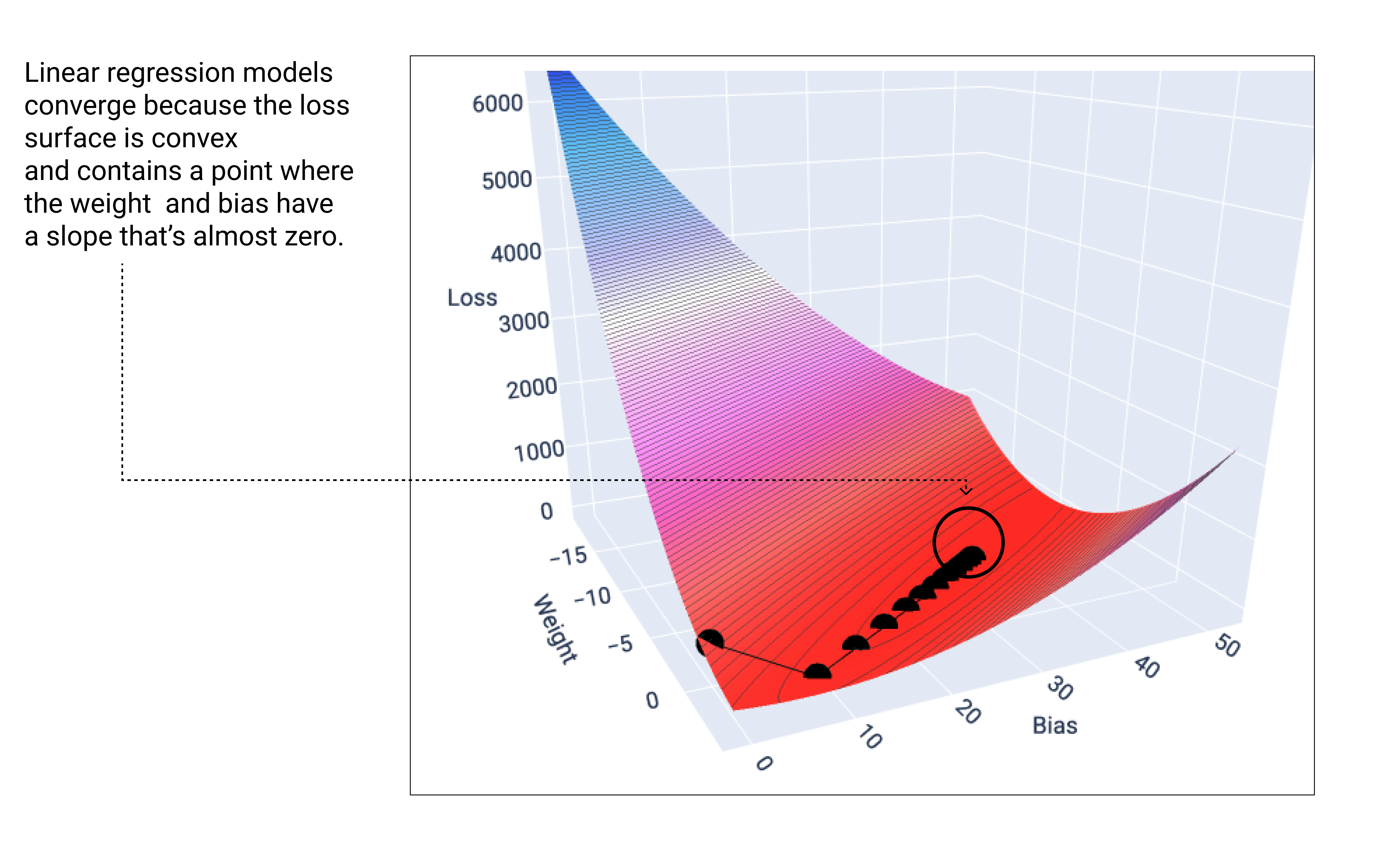
Рисунок 19. Графік втрат, що показує точки градієнтного спуску, які зупиняються в його найнижчій точці.
Зверніть увагу, що чорні точки утворюють точну форму кривої втрат: демонструють крутий спад перед поступовим нахилом униз до досягнення найнижчої точки на поверхні втрат.
Зверніть увагу: для кожного значення ваги й зсуву модель майже завжди знаходить не точне мінімальне число, а дуже близьке до нього. Також важливо знати, що мінімальне число для значень ваги й зсуву відповідає не нульовим втратам, а числу, яке дає найменші втрати для цього параметра.
Використовуючи значення ваги й зсуву, які дають найменші втрати (у нас це вага –5,44 і зсув 35,94), можна побудувати графік моделі, щоб побачити, наскільки добре вона пристосовується до даних.
Рисунок 20. Модель, зображена на графіку з використанням значень ваги й зсуву, які дають найменші втрати.
Це найкраща модель для набору даних, оскільки інші значення ваги й зсуву не призводять до створення моделі з меншими втратами.