梯度下降是一種數學技術,可反覆找出權重和偏誤,產生損失最低的模型。梯度下降會重複執行下列程序 (次數由使用者定義),找出最佳權重和偏差。
模型會先以接近零的隨機權重和偏差值開始訓練,然後重複執行下列步驟:
使用目前的權重和偏差計算損失。
判斷要朝哪個方向移動權重和偏誤,才能減少損失。
朝減少損失的方向,稍微移動權重和偏差值。
返回步驟一並重複執行程序,直到模型無法再減少損失為止。
下圖概述梯度下降執行的疊代步驟,目的是找出可產生最低損失模型權重和偏差。
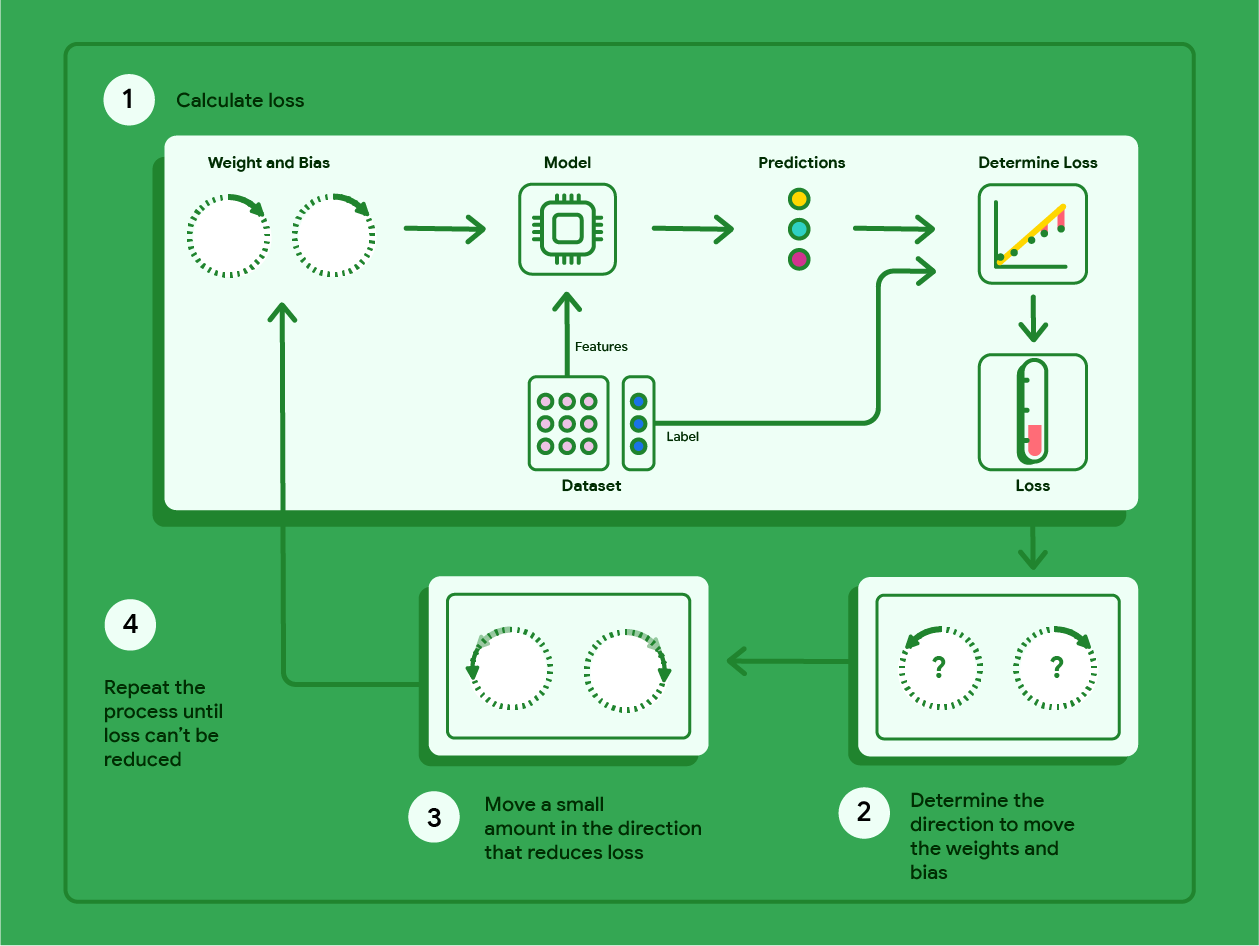
圖 11. 梯度下降法是疊代程序,可找出產生最低損失模型時的權重和偏差。
按一下加號圖示,進一步瞭解梯度下降背後的數學原理。
具體來說,我們可以透過下列七個範例的小型燃油效率資料集,逐步瞭解梯度下降步驟,並以 均方誤差 (MSE) 做為損失指標:
| 以千為單位的磅數 (功能) | 每加侖英里 (標籤) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
- 模型會將權重和偏誤設為零,然後開始訓練:
- 使用目前的模型參數計算 MSE 損失:
- 計算每個權重和偏差的損失函數切線斜率:
- 朝負斜率方向移動少量,即可取得下一個權重和偏差。目前,我們會任意將「少量」定義為 0.01:
按一下加號圖示,瞭解如何計算斜率。
如要取得權重和偏誤的切線斜率,請根據權重和偏誤得出損失函式的導數,然後解出方程式。
我們將預測方程式寫成:
$ f_{w,b}(x) = (w*x)+b $。
我們會將實際值寫為:$ y $。
我們會使用以下公式計算 MSE:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
其中 $i$ 代表第 $i$ 個訓練範例,$M$ 代表範例數量。
損失函式對權重的導數可寫成:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
並評估為:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
首先,我們會將每個預測值減去實際值,然後乘以特徵值的兩倍。然後將總和除以範例數量。 結果是與權重值相切的直線斜率。
如果我們以權重和偏差值等於零來解這道方程式,會得到 -119.7 的線條斜率。
偏差導數
損失函式對偏差的導數可寫成:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
並評估為:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
首先,我們會將每個預測值減去實際值,然後乘以 2。然後將總和除以範例數量。結果是與偏差值相切的直線斜率。
如果我們以權重和偏差值等於零來解這個方程式,會得到 -34.3 的直線斜率。
使用新的權重和偏差計算損失並重複。完成六次疊代程序後,我們會得到下列權重、偏差和損失:
| 疊代作業 | 重量 | 偏誤 | 損失 (均方誤差) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | 3.09 | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
您會發現,每次更新權重和偏差後,損失都會降低。 在本例中,我們在六次疊代後停止。在實務上,模型會訓練到收斂為止。模型收斂後,額外的疊代不會再減少損失,因為梯度下降已找到可將損失降至最低的權重和偏差。
如果模型在收斂後繼續訓練,損失就會開始小幅波動,因為模型會持續更新參數,使其接近最低值。這會導致難以驗證模型是否確實已收斂。如要確認模型是否已收斂,請繼續訓練,直到損失穩定為止。
模型收斂和損失曲線
訓練模型時,您通常會查看損失曲線,判斷模型是否已收斂。損失曲線會顯示模型訓練時的損失變化。以下是典型的損失曲線。Y 軸代表損失,X 軸代表疊代:
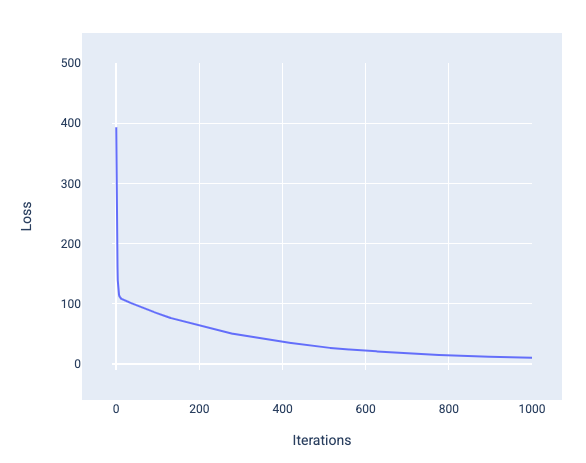
圖 12. 損失曲線:模型在第 1,000 次疊代左右收斂。
您可以看到,在前幾次疊代期間,損失大幅減少,然後逐漸減少,在第 1,000 次疊代左右趨於平緩。經過 1,000 次疊代後,我們大致可以確定模型已收斂。
在下圖中,我們繪製了訓練過程中的三個時間點模型:開始、中間和結束。在訓練過程中,以快照形式呈現模型狀態,可強化權重和偏差更新、減少損失及模型收斂之間的連結。
在圖中,我們使用特定疊代作業的衍生權重和偏差,代表模型。在含有資料點和模型快照的圖表中,從模型到資料點的藍色損失線會顯示損失量。線條越長,損失就越大。
從下圖中可以看出,模型在第二次疊代時,由於損失量過高,因此無法做出準確預測。
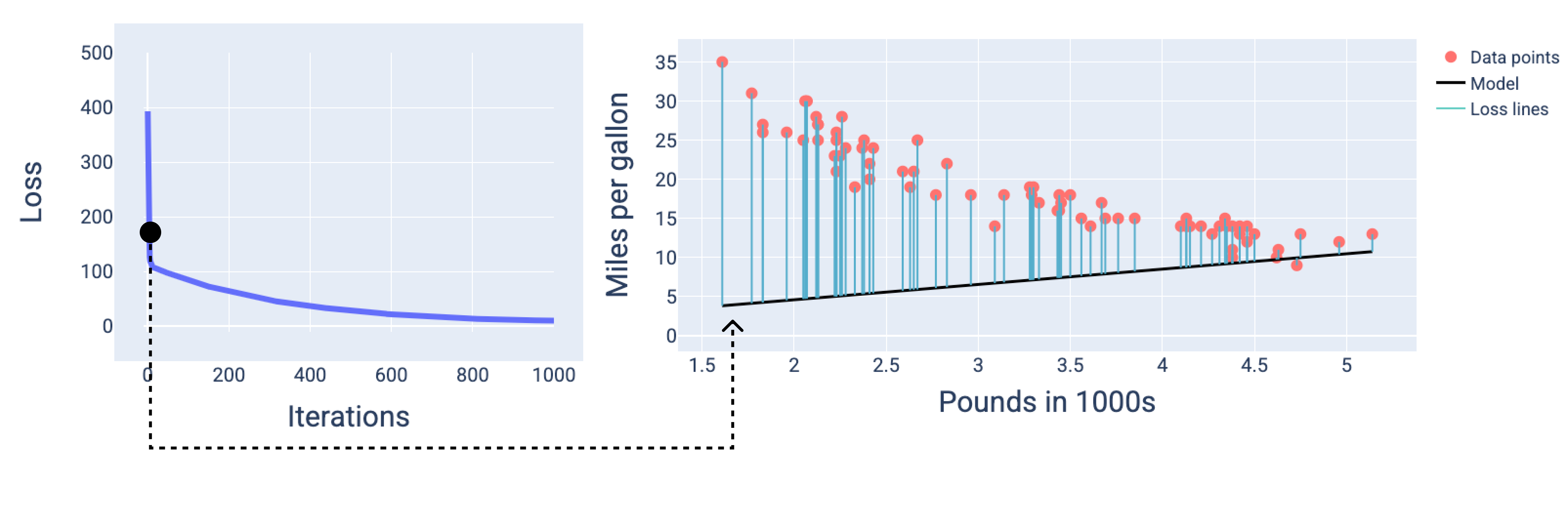
圖 13. 訓練程序開始時的模型損失曲線和快照。
在大約第 400 次疊代時,我們可以看到梯度下降法已找出可產生更優質模型的權重和偏差。
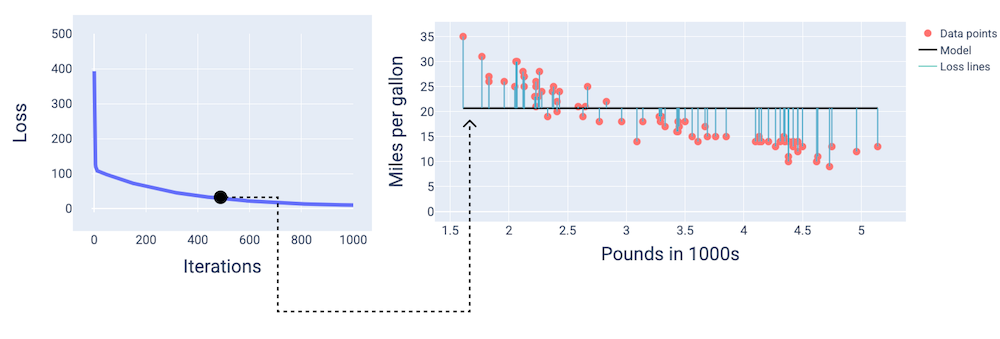
圖 14.損失曲線和模型快照,約在訓練中途。
大約在第 1,000 次疊代時,我們可以看到模型已收斂,產生損失值最低的模型。
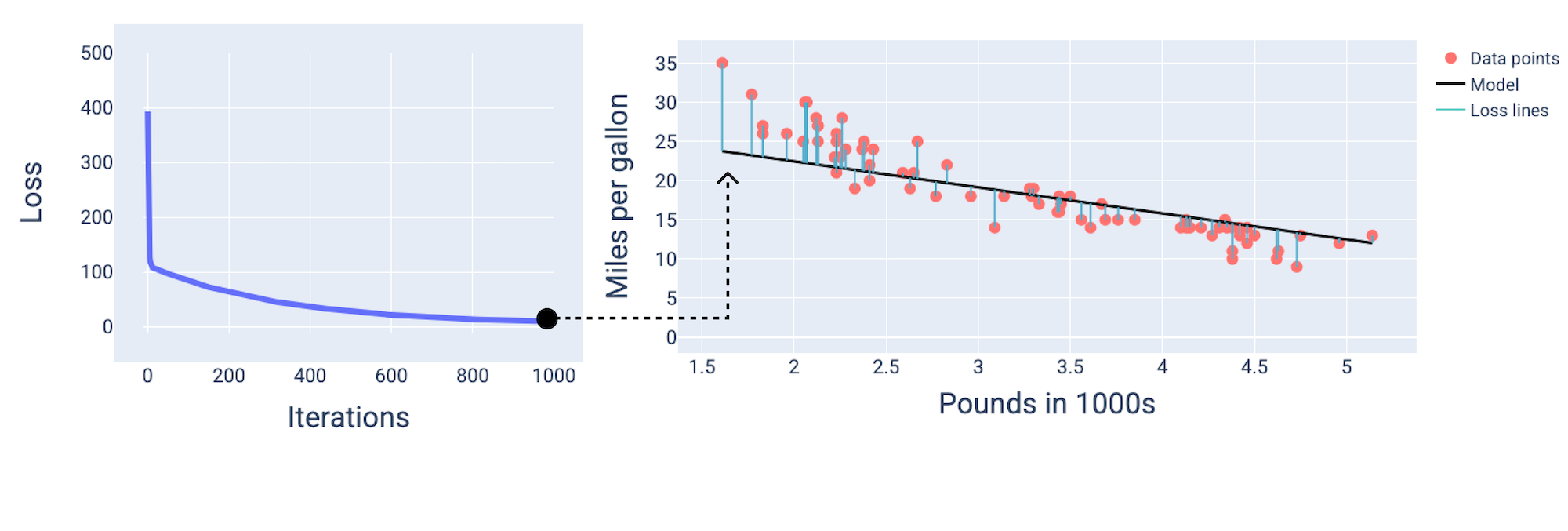
圖 15.訓練程序即將結束時的模型損失曲線和快照。
練習:確認你的理解程度
收斂和凸函數
線性模型的損失函數一律會產生凸面。因此,當線性迴歸模型收斂時,我們知道模型已找出可產生最低損失的權重和偏差。
如果我們繪製具有一項特徵的模型損失曲面圖,會發現其凸面形狀。以下是假設的每加侖英里數資料集的損失曲面。X 軸代表權重、Y 軸代表偏差,而 Z 軸代表損失:
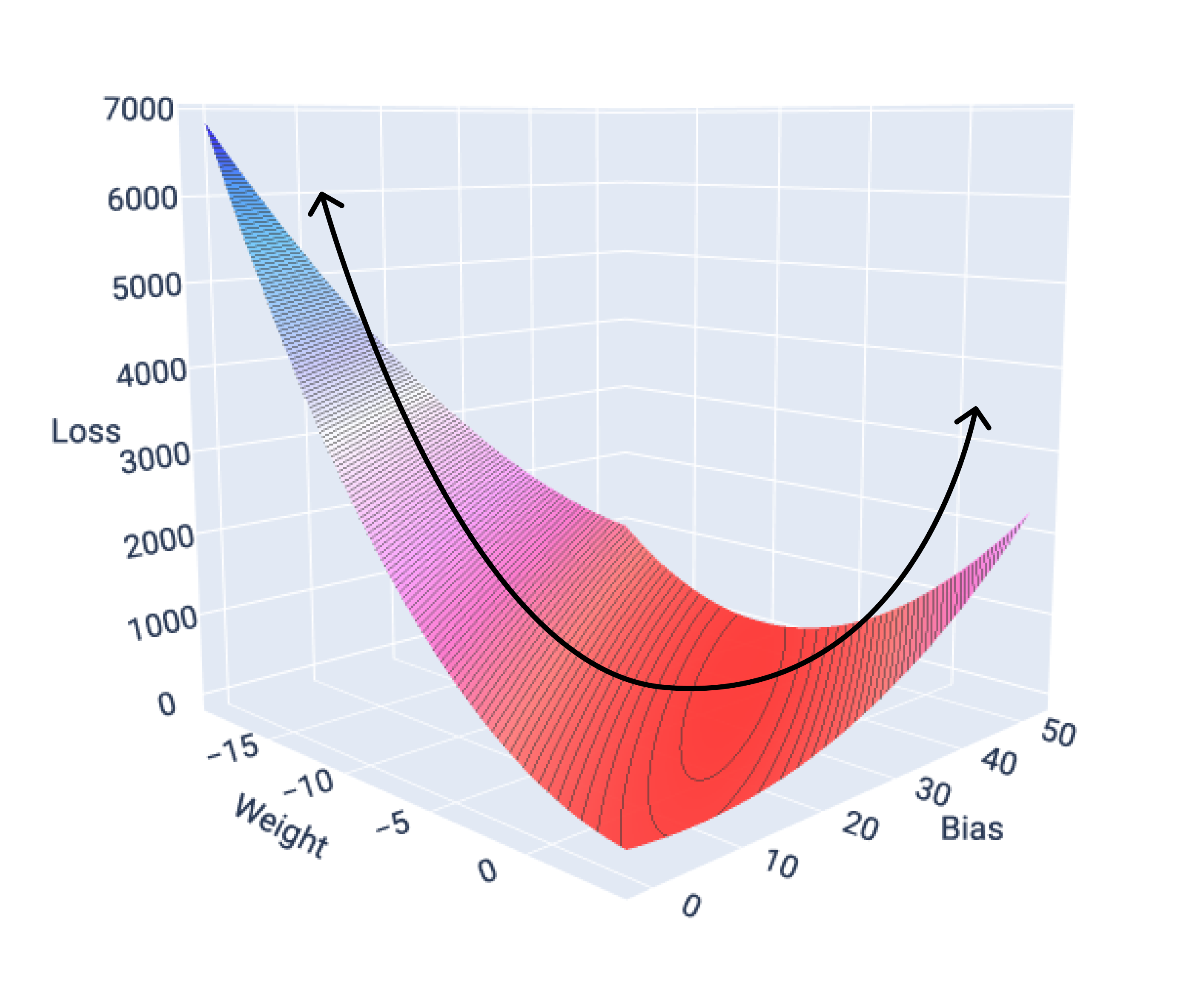
圖 16. 顯示凸面形狀的損失曲面。
在本例中,權重為 -5.44,偏誤為 35.94,在 5.54 時產生最低損失:
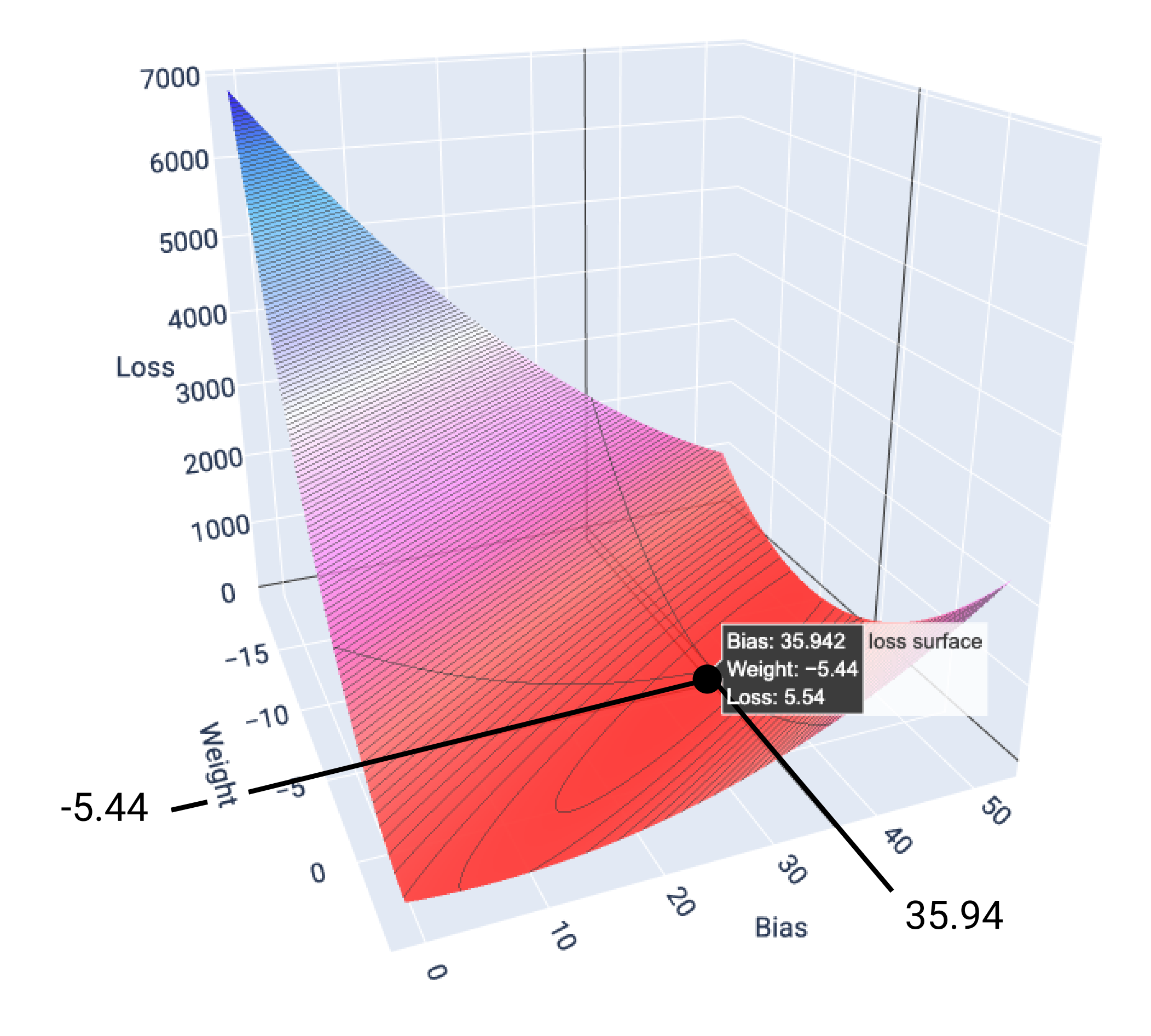
圖 17. 損失曲面,顯示產生最低損失的權重和偏差值。
線性模型找到最低損失時,就會收斂。因此,額外的疊代只會導致梯度下降,使權重和偏差值在最小值附近小幅變動。如果我們在梯度下降期間繪製權重和偏差點的圖表,這些點看起來就像一顆球從山上滾下來,最後停在沒有下坡的點。
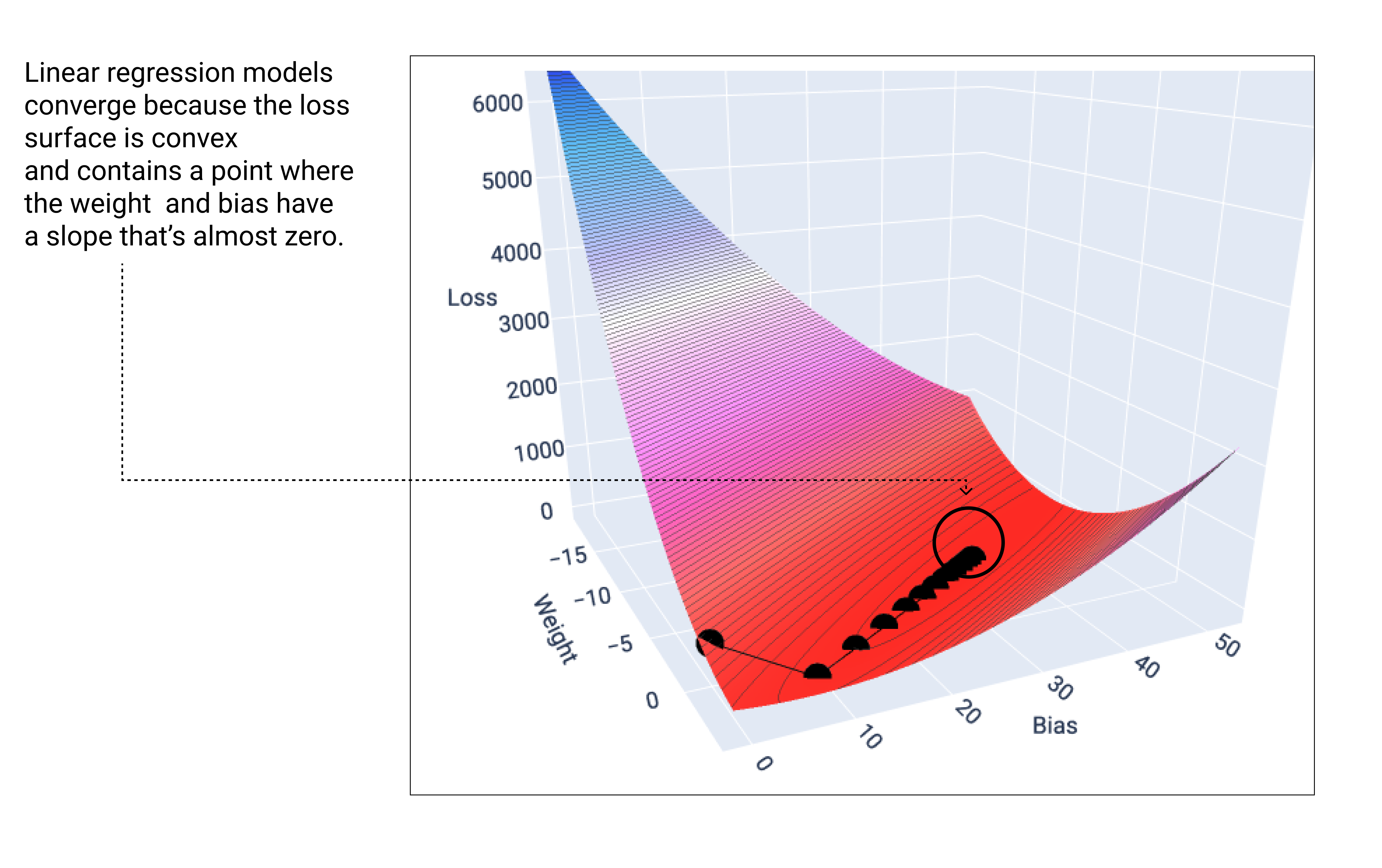
圖 18. 損失圖表:顯示梯度下降點在圖表最低點停止。
請注意,黑色損失點會形成損失曲線的確切形狀:先大幅下降,然後逐漸向下傾斜,直到損失曲面上的最低點。
請注意,模型幾乎不會找出每個權重和偏差的確切最小值,而是找出非常接近的值。此外,權重和偏差的最小值並非對應到零損失,而是產生該參數最低損失的值,這點也請務必注意。
使用產生最低損失的權重和偏差值 (本例中為權重 -5.44 和偏差值 35.94),我們可以繪製模型圖表,瞭解模型與資料的相符程度:
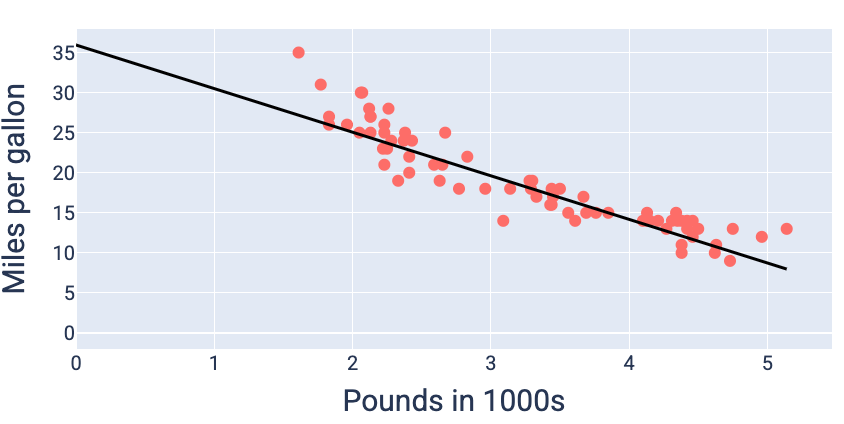
圖 19. 使用產生最低損失的權重和偏差值繪製的模型圖。
這是這個資料集的最佳模型,因為沒有其他權重和偏差值能產生損失較低的模型。
