গ্রেডিয়েন্ট ডিসেন্ট হল একটি গাণিতিক কৌশল যা পুনরাবৃত্তিমূলকভাবে ওজন এবং পক্ষপাত খুঁজে পায় যা সর্বনিম্ন ক্ষতির সাথে মডেলটি তৈরি করে। গ্রেডিয়েন্ট ডিসেন্ট অনেকগুলি ব্যবহারকারী-সংজ্ঞায়িত পুনরাবৃত্তির জন্য নিম্নলিখিত প্রক্রিয়াটি পুনরাবৃত্তি করে সর্বোত্তম ওজন এবং পক্ষপাত খুঁজে পায়।
মডেলটি শূন্যের কাছাকাছি এলোমেলো ওজন এবং পক্ষপাতের সাথে প্রশিক্ষণ শুরু করে এবং তারপরে নিম্নলিখিত পদক্ষেপগুলি পুনরাবৃত্তি করে:
বর্তমান ওজন এবং পক্ষপাত দিয়ে ক্ষতি গণনা করুন।
ওজন এবং পক্ষপাতগুলি সরানোর দিক নির্ধারণ করুন যা ক্ষতি হ্রাস করে।
ওজন এবং পক্ষপাতের মানগুলিকে সেই দিকে নিয়ে যান যা ক্ষতি হ্রাস করে।
প্রথম ধাপে ফিরে যান এবং প্রক্রিয়াটি পুনরাবৃত্তি করুন যতক্ষণ না মডেলটি আর ক্ষতি কমাতে না পারে।
নীচের চিত্রটি সর্বনিম্ন ক্ষতি সহ মডেল তৈরি করে ওজন এবং পক্ষপাত খুঁজে বের করতে গ্রেডিয়েন্ট ডিসেন্ট সঞ্চালিত পুনরাবৃত্তিমূলক পদক্ষেপগুলির রূপরেখা দেয়।
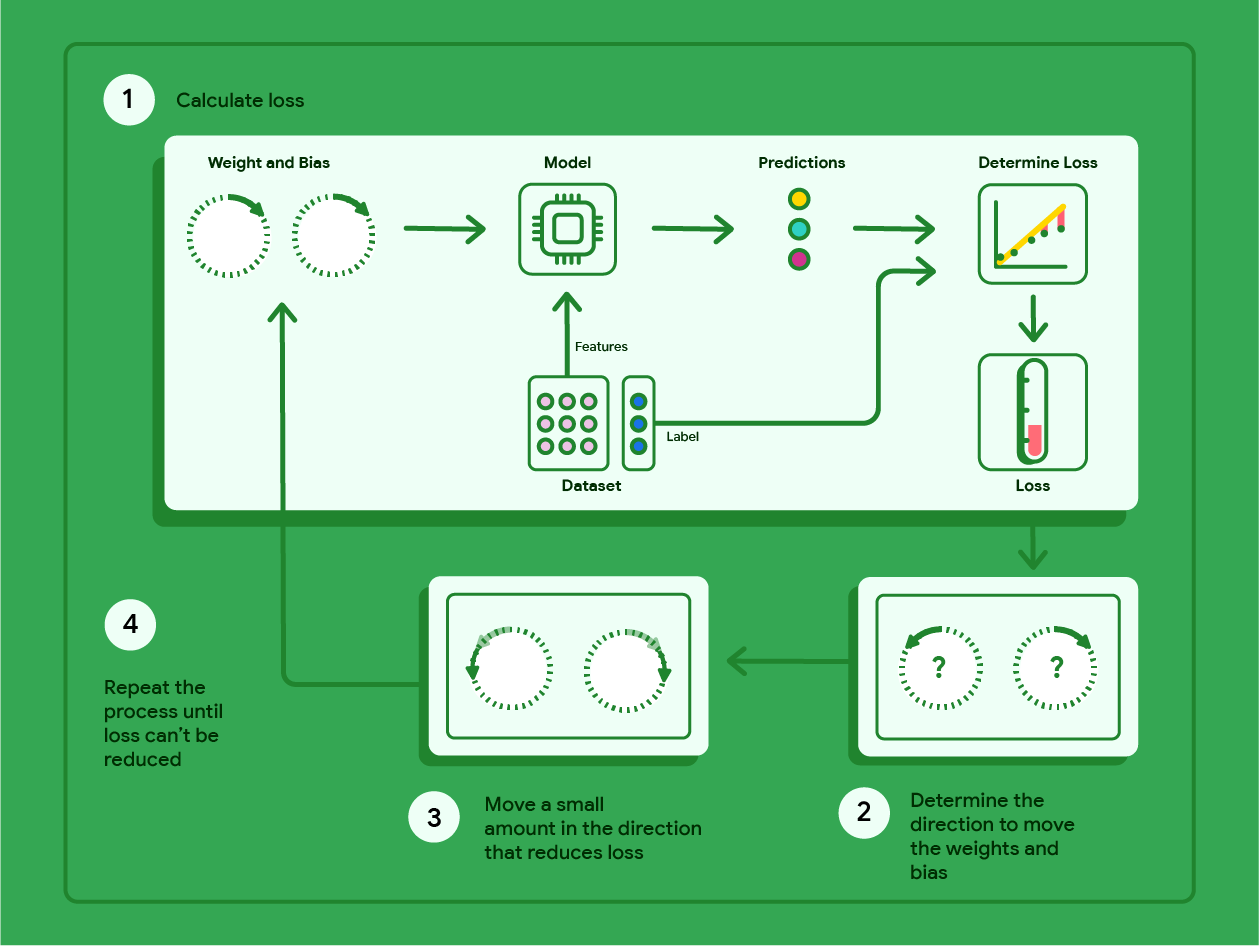
চিত্র 11 । গ্রেডিয়েন্ট ডিসেন্ট হল একটি পুনরাবৃত্ত প্রক্রিয়া যা ওজন এবং পক্ষপাত খুঁজে পায় যা সর্বনিম্ন ক্ষতি সহ মডেল তৈরি করে।
গ্রেডিয়েন্ট ডিসেন্টের পিছনের গণিত সম্পর্কে আরও জানতে প্লাস আইকনে ক্লিক করুন।
একটি কংক্রিট স্তরে, আমরা একটি ছোট ডেটাসেট ব্যবহার করে গ্রেডিয়েন্ট ডিসেন্ট ধাপে হাঁটতে পারি যার সাতটি উদাহরণ সহ একটি গাড়ির পাউন্ডে ভারীতা এবং এর মাইল প্রতি গ্যালন রেটিং:
| পাউন্ড ইন 1000 (বৈশিষ্ট্য) | মাইলস প্রতি গ্যালন (লেবেল) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| ৪.৩৪ | 15 |
| ৪.৪২ | 14 |
| 2.37 | 24 |
- মডেলটি ওজন এবং পক্ষপাত শূন্যে সেট করে প্রশিক্ষণ শুরু করে:
- বর্তমান মডেল প্যারামিটারের সাথে MSE ক্ষতি গণনা করুন:
- প্রতিটি ওজন এবং পক্ষপাতের ক্ষতি ফাংশনে স্পর্শকের ঢাল গণনা করুন:
- পরবর্তী ওজন এবং পক্ষপাত পেতে নেতিবাচক ঢালের দিকে একটি ছোট পরিমাণ সরান। আপাতত, আমরা নির্বিচারে 0.01 হিসাবে "ছোট পরিমাণ" সংজ্ঞায়িত করব:
ঢাল গণনা সম্পর্কে জানতে প্লাস আইকনে ক্লিক করুন।
ওজন এবং পক্ষপাতের স্পর্শক রেখার ঢাল পেতে, আমরা ওজন এবং পক্ষপাতের সাপেক্ষে ক্ষতি ফাংশনের ডেরিভেটিভ নিই এবং তারপর সমীকরণগুলি সমাধান করি।
আমরা একটি ভবিষ্যদ্বাণী করার জন্য সমীকরণ লিখব:
$ f_{w,b}(x) = (w*x)+b $।
আমরা প্রকৃত মান লিখব: $y $।
আমরা ব্যবহার করে MSE গণনা করব:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
যেখানে $i$ $ith$ প্রশিক্ষণের উদাহরণ এবং $M$ উদাহরণের সংখ্যা উপস্থাপন করে।
ওজন সাপেক্ষে লস ফাংশনের ডেরিভেটিভ এভাবে লেখা হয়:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
এবং মূল্যায়ন করে:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
প্রথমে আমরা প্রতিটি ভবিষ্যদ্বাণীকৃত মান বিয়োগ করে প্রকৃত মান যোগ করি এবং তারপর বৈশিষ্ট্য মানের দুই গুণ দ্বারা গুণ করি। তারপর যোগফলকে উদাহরণের সংখ্যা দিয়ে ভাগ করি। ফলাফল হল ওজনের মানের স্পর্শক রেখার ঢাল।
যদি আমরা এই সমীকরণটি শূন্যের সমান ওজন এবং পক্ষপাত দিয়ে সমাধান করি, তাহলে আমরা লাইনের ঢালের জন্য -119.7 পাব।
বায়াস ডেরিভেটিভ পক্ষপাতের সাপেক্ষে লস ফাংশনের ডেরিভেটিভ এভাবে লেখা হয়:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
এবং মূল্যায়ন করে:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
প্রথমে আমরা প্রতিটি ভবিষ্যদ্বাণীকৃত মান বিয়োগ করে প্রকৃত মান যোগ করি এবং তারপর এটিকে দুই দ্বারা গুণ করি। তারপর যোগফলকে উদাহরণের সংখ্যা দিয়ে ভাগ করি। ফলাফল হল পক্ষপাতের মানের সাথে রেখার স্পর্শকের ঢাল।
যদি আমরা এই সমীকরণটি শূন্যের সমান ওজন এবং পক্ষপাত দিয়ে সমাধান করি, তাহলে আমরা লাইনের ঢালের জন্য -34.3 পাব।
ক্ষতি গণনা করতে এবং পুনরাবৃত্তি করতে নতুন ওজন এবং পক্ষপাত ব্যবহার করুন। ছয়টি পুনরাবৃত্তির জন্য প্রক্রিয়াটি সম্পূর্ণ করে, আমরা নিম্নলিখিত ওজন, পক্ষপাত এবং ক্ষতি পাব:
| পুনরাবৃত্তি | ওজন | পক্ষপাত | ক্ষতি (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1.20 | 0.34 | 170.84 |
| 3 | 2.05 | 0.59 | 103.17 |
| 4 | 2.66 | 0.78 | 68.70 |
| 5 | ৩.০৯ | 0.91 | 51.13 |
| 6 | 3.40 | 1.01 | 42.17 |
আপনি দেখতে পাচ্ছেন যে প্রতিটি আপডেট করা ওজন এবং পক্ষপাতের সাথে ক্ষতি কম হয়। এই উদাহরণে, আমরা ছয়টি পুনরাবৃত্তির পরে থামলাম। অনুশীলনে, একটি মডেল প্রশিক্ষন করে যতক্ষণ না এটি একত্রিত হয় । যখন একটি মডেল একত্রিত হয়, তখন অতিরিক্ত পুনরাবৃত্তি ক্ষতিকে কমিয়ে দেয় না কারণ গ্রেডিয়েন্ট ডিসেন্ট ওজন এবং পক্ষপাত খুঁজে পেয়েছে যা প্রায় ক্ষতি কমিয়ে দেয়।
যদি মডেলটি অতীতের কনভারজেন্সকে প্রশিক্ষিত করতে থাকে, তাহলে ক্ষতি অল্প পরিমাণে ওঠানামা করতে শুরু করে কারণ মডেল ক্রমাগত তাদের সর্বনিম্ন মানের চারপাশে পরামিতি আপডেট করে। এটি মডেলটি আসলে একত্রিত হয়েছে তা যাচাই করা কঠিন করে তুলতে পারে। মডেলটি একত্রিত হয়েছে তা নিশ্চিত করতে, ক্ষতি স্থিতিশীল না হওয়া পর্যন্ত আপনি প্রশিক্ষণ চালিয়ে যেতে চাইবেন।
মডেল কনভারজেন্স এবং ক্ষতি বক্ররেখা
একটি মডেলকে প্রশিক্ষণ দেওয়ার সময়, মডেলটি একত্রিত হয়েছে কিনা তা নির্ধারণ করতে আপনি প্রায়শই ক্ষতির বক্ররেখার দিকে তাকাবেন। ক্ষতির বক্ররেখা দেখায় কিভাবে মডেল ট্রেনের সাথে সাথে ক্ষতি পরিবর্তিত হয়। নিম্নে একটি সাধারণ ক্ষতি বক্ররেখা কেমন দেখায়। ক্ষতি y-অক্ষে এবং পুনরাবৃত্তিগুলি x-অক্ষে রয়েছে:
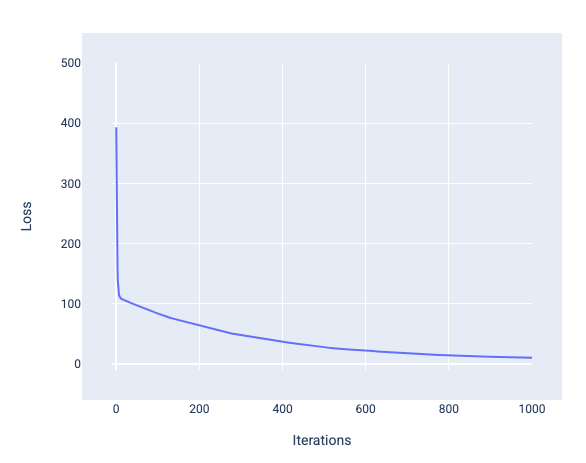
চিত্র 12 । লস বক্ররেখা 1,000 তম-পুনরাবৃত্তি চিহ্নের চারপাশে রূপান্তরিত মডেলটিকে দেখাচ্ছে৷
আপনি দেখতে পাচ্ছেন যে প্রথম কয়েকটি পুনরাবৃত্তির সময় ক্ষতি নাটকীয়ভাবে হ্রাস পায়, তারপর 1,000 তম-পুনরাবৃত্তি চিহ্নের চারপাশে সমতল হওয়ার আগে ধীরে ধীরে হ্রাস পায়। 1,000 পুনরাবৃত্তির পরে, আমরা বেশিরভাগই নিশ্চিত হতে পারি যে মডেলটি একত্রিত হয়েছে।
নিম্নলিখিত পরিসংখ্যানগুলিতে, আমরা প্রশিক্ষণ প্রক্রিয়া চলাকালীন তিনটি পয়েন্টে মডেলটি আঁকি: শুরু, মধ্য এবং শেষ। ট্রেনিং প্রক্রিয়া চলাকালীন স্ন্যাপশটে মডেলের অবস্থাকে ভিজ্যুয়ালাইজ করা ওজন এবং পক্ষপাত আপডেট করা, ক্ষতি কমানো এবং মডেল কনভারজেন্সের মধ্যে সংযোগকে দৃঢ় করে।
পরিসংখ্যানে, আমরা মডেলের প্রতিনিধিত্ব করতে একটি নির্দিষ্ট পুনরাবৃত্তিতে প্রাপ্ত ওজন এবং পক্ষপাত ব্যবহার করি। ডেটা পয়েন্ট এবং মডেল স্ন্যাপশট সহ গ্রাফে, মডেল থেকে ডেটা পয়েন্ট পর্যন্ত নীল ক্ষতির লাইনগুলি ক্ষতির পরিমাণ দেখায়। লাইন যত দীর্ঘ হবে, ক্ষতি তত বেশি হবে।
নিম্নলিখিত চিত্রে, আমরা দেখতে পাচ্ছি যে দ্বিতীয় পুনরাবৃত্তির আশেপাশে মডেলটি ক্ষতির উচ্চ পরিমাণের কারণে ভবিষ্যদ্বাণী করতে ভাল হবে না।
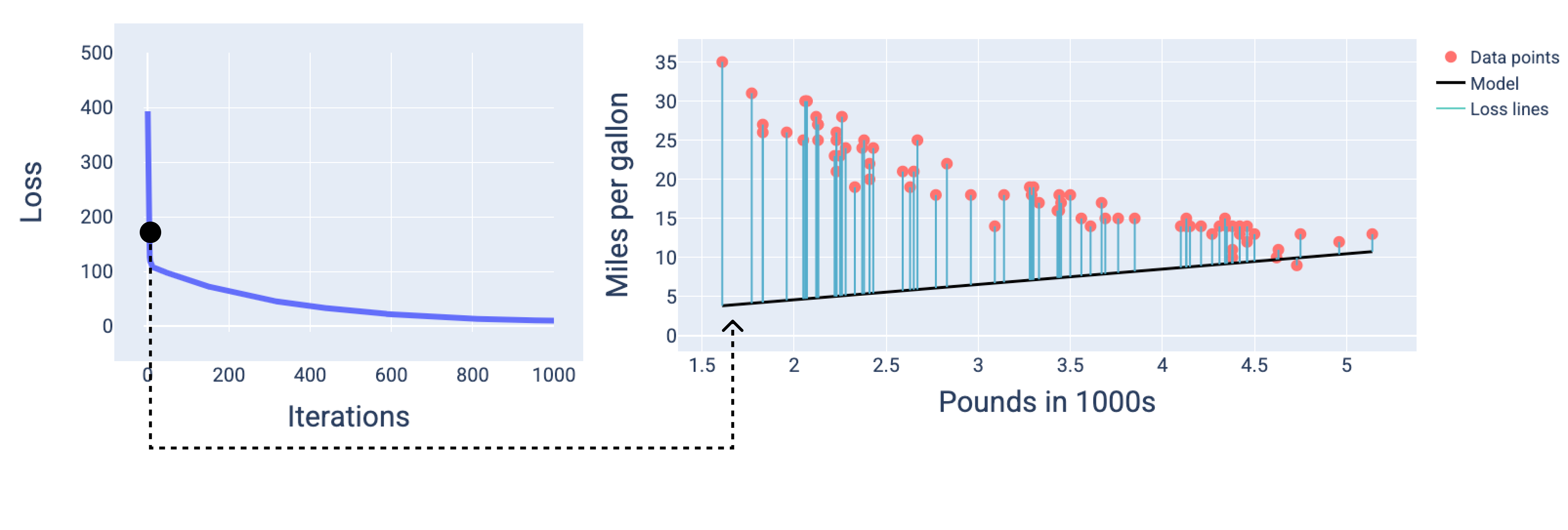
চিত্র 13 । প্রশিক্ষণ প্রক্রিয়ার শুরুতে লস বক্ররেখা এবং মডেলের স্ন্যাপশট।
প্রায় 400 তম পুনরাবৃত্তিতে, আমরা দেখতে পাচ্ছি যে গ্রেডিয়েন্ট ডিসেন্ট ওজন এবং পক্ষপাত খুঁজে পেয়েছে যা একটি ভাল মডেল তৈরি করে।
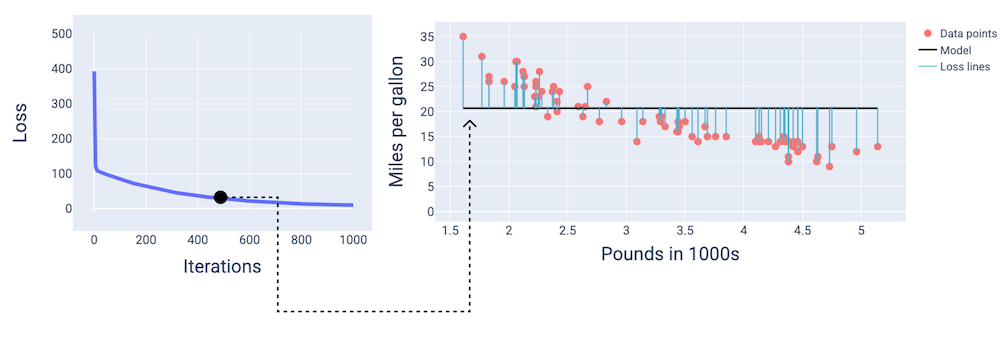
চিত্র 14 । প্রশিক্ষণের মাঝপথে লস কার্ভ এবং মডেলের স্ন্যাপশট।
এবং প্রায় 1,000 তম-পুনরাবৃত্তিতে, আমরা দেখতে পাচ্ছি যে মডেলটি একত্রিত হয়েছে, সম্ভাব্য সর্বনিম্ন ক্ষতি সহ একটি মডেল তৈরি করেছে।
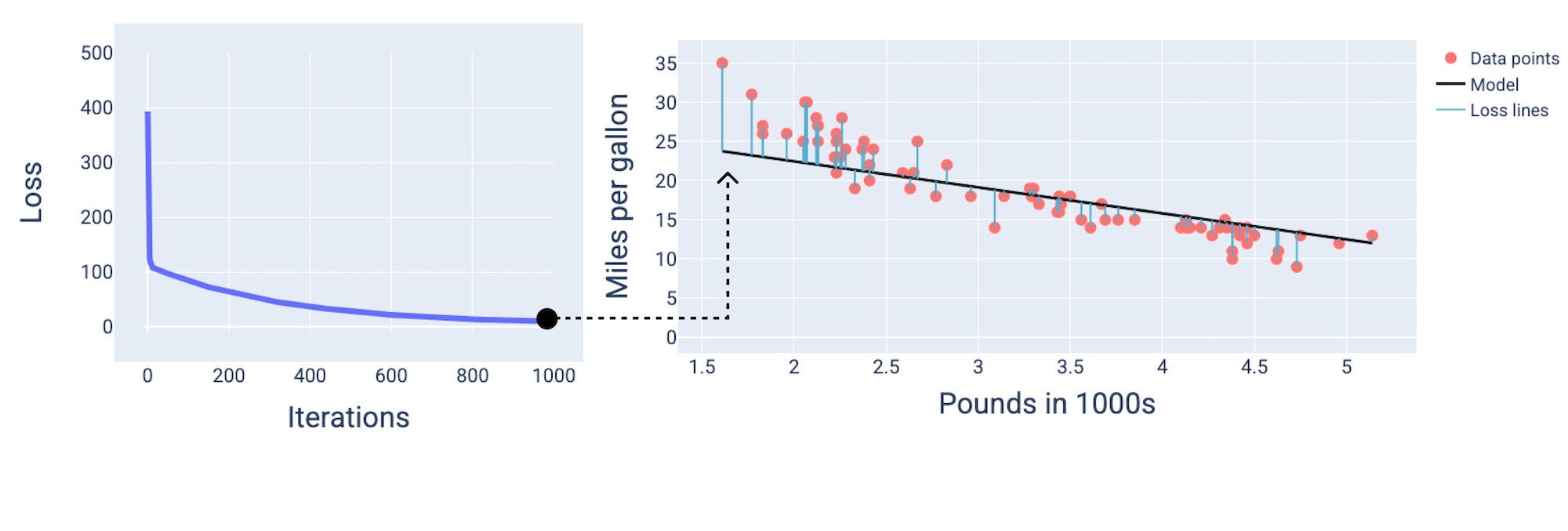
চিত্র 15 । প্রশিক্ষণ প্রক্রিয়ার শেষের কাছাকাছি মডেলের ক্ষতি বক্ররেখা এবং স্ন্যাপশট।
অনুশীলন: আপনার বোঝার পরীক্ষা করুন
কনভারজেন্স এবং উত্তল ফাংশন
লিনিয়ার মডেলের ক্ষতি ফাংশন সবসময় একটি উত্তল পৃষ্ঠ তৈরি করে। এই সম্পত্তির ফলস্বরূপ, যখন একটি রৈখিক রিগ্রেশন মডেল একত্রিত হয়, আমরা জানি যে মডেলটি ওজন এবং পক্ষপাত খুঁজে পেয়েছে যা সর্বনিম্ন ক্ষতি করে।
যদি আমরা একটি বৈশিষ্ট্য সহ একটি মডেলের ক্ষতির পৃষ্ঠকে গ্রাফ করি, তাহলে আমরা এর উত্তল আকৃতি দেখতে পাব। গ্যালন ডেটাসেট প্রতি একটি অনুমানিক মাইলের জন্য ক্ষতির পৃষ্ঠটি নিম্নরূপ। ওজন x-অক্ষে, পক্ষপাত y-অক্ষে, এবং ক্ষতি z-অক্ষে:
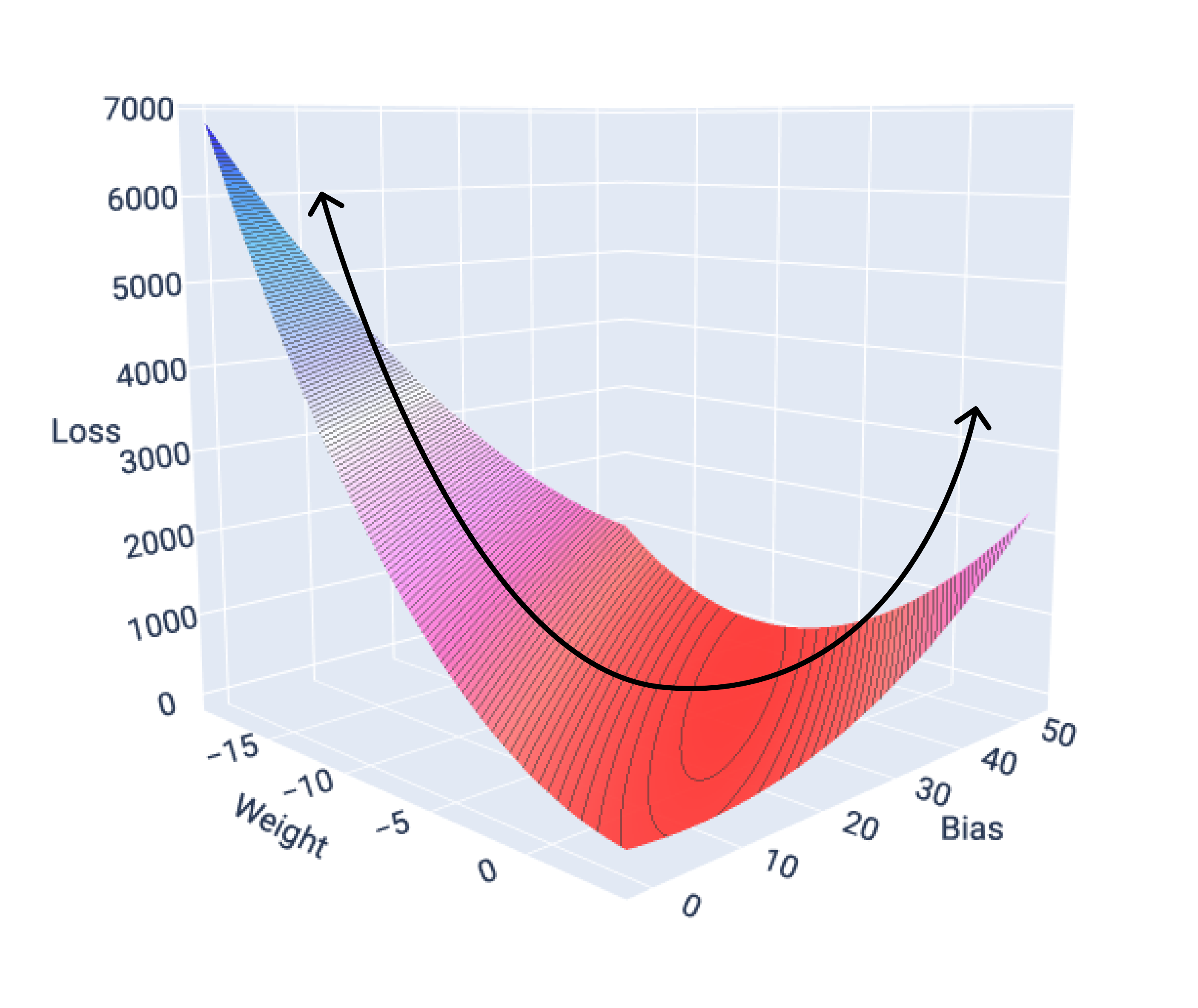
চিত্র 16. ক্ষতির পৃষ্ঠ যা তার উত্তল আকৃতি দেখায়।
এই উদাহরণে, -5.44-এর ওজন এবং 35.94-এর পক্ষপাত 5.54-এ সর্বনিম্ন ক্ষতি তৈরি করে:
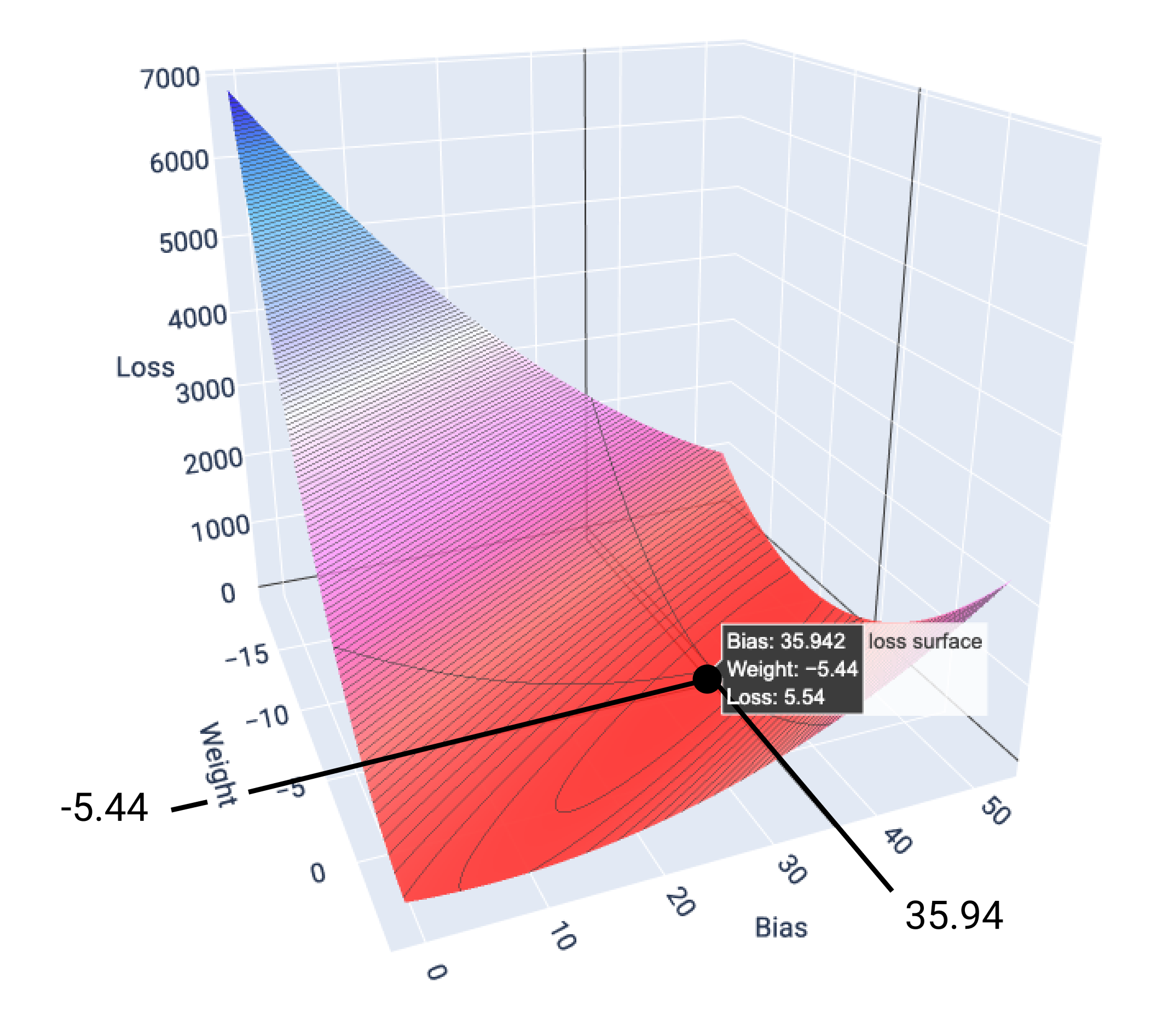
চিত্র 17 । ক্ষতির পৃষ্ঠ ওজন এবং পক্ষপাতের মানগুলি দেখায় যা সর্বনিম্ন ক্ষতি করে।
একটি লিনিয়ার মডেল একত্রিত হয় যখন এটি সর্বনিম্ন ক্ষতি পাওয়া যায়। অতএব, অতিরিক্ত পুনরাবৃত্তির কারণে শুধুমাত্র গ্রেডিয়েন্ট ডিসেন্ট ওজন এবং পক্ষপাতের মানগুলিকে ন্যূনতমের চারপাশে খুব কম পরিমাণে স্থানান্তরিত করে। গ্রেডিয়েন্ট ডিসেন্টের সময় যদি আমরা ওজন এবং বায়াস পয়েন্টগুলি গ্রাফ করি, তাহলে পয়েন্টগুলি একটি পাহাড়ের নিচে গড়িয়ে যাওয়া বলের মতো দেখাবে, অবশেষে সেই বিন্দুতে থামবে যেখানে আর নিচের দিকে ঢাল নেই।
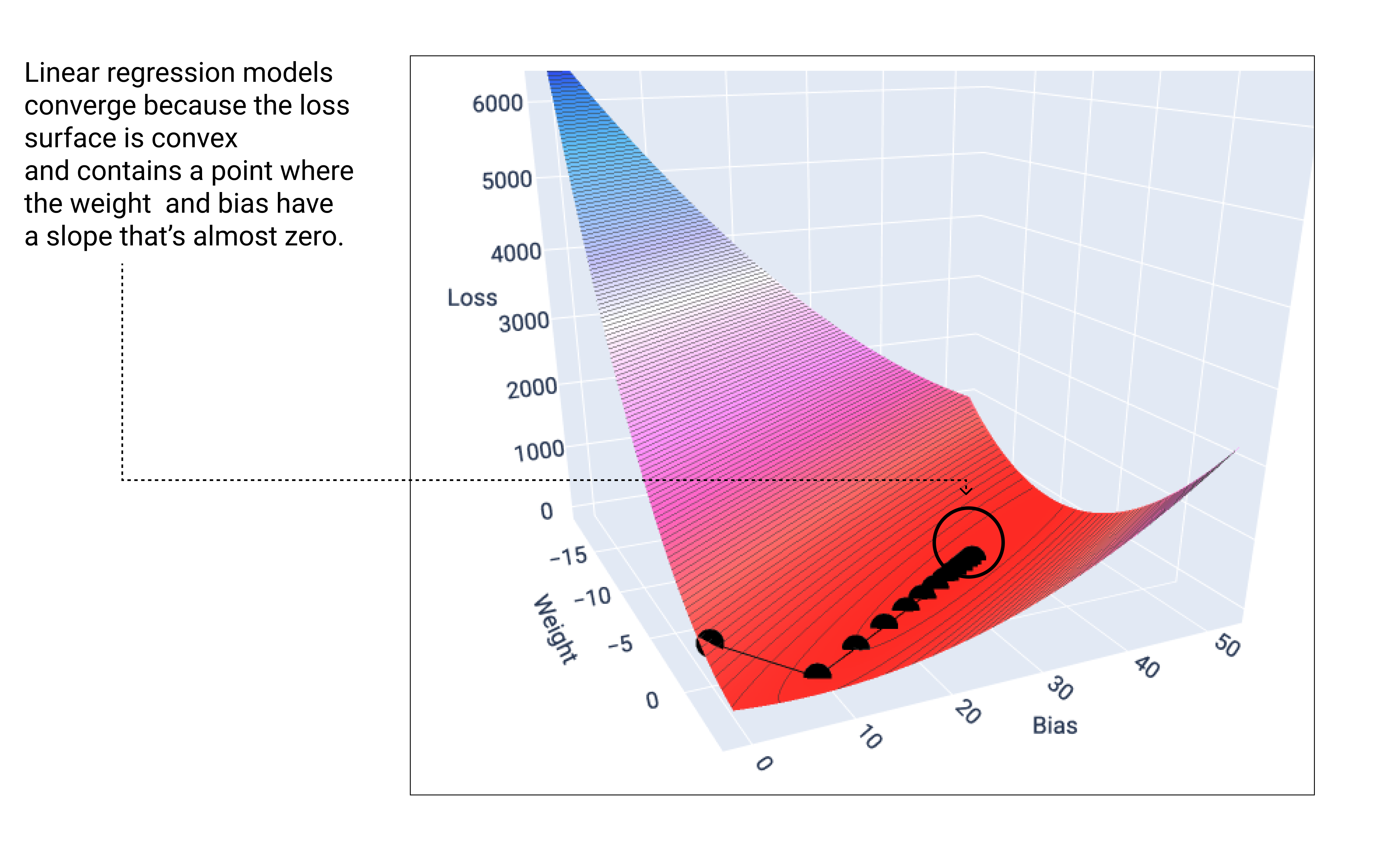
চিত্র 18 । হারের গ্রাফ গ্রাফের সর্বনিম্ন বিন্দুতে থেমে থাকা গ্রেডিয়েন্ট ডিসেন্ট পয়েন্ট দেখায়।
লক্ষ্য করুন যে কালো ক্ষতির পয়েন্টগুলি ক্ষতির বক্ররেখার সঠিক আকৃতি তৈরি করে: ধীরে ধীরে ঢালু হওয়ার আগে একটি খাড়া পতন যতক্ষণ না তারা ক্ষতির পৃষ্ঠের সর্বনিম্ন বিন্দুতে পৌঁছেছে।
এটি লক্ষ করা গুরুত্বপূর্ণ যে মডেলটি প্রায় কখনই প্রতিটি ওজন এবং পক্ষপাতের জন্য সঠিক ন্যূনতম খুঁজে পায় না, বরং এটির খুব কাছাকাছি একটি মান খুঁজে পায়। এটাও মনে রাখা গুরুত্বপূর্ণ যে ওজন এবং পক্ষপাতের জন্য ন্যূনতম শূন্য ক্ষতির সাথে সঙ্গতিপূর্ণ নয়, শুধুমাত্র একটি মান যা সেই প্যারামিটারের জন্য সর্বনিম্ন ক্ষতি তৈরি করে।
ওজন এবং পক্ষপাতের মানগুলি ব্যবহার করে যা সর্বনিম্ন ক্ষতি করে—এই ক্ষেত্রে একটি ওজন -5.44 এবং একটি পক্ষপাত 35.94—আমরা মডেলটি গ্রাফ করতে পারি যে এটি ডেটার সাথে কতটা মানানসই:
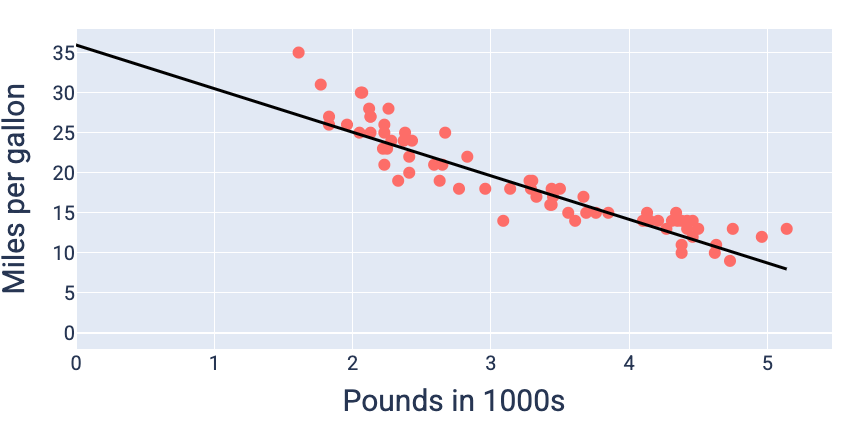
চিত্র 19. ওজন এবং পক্ষপাতের মান ব্যবহার করে মডেল গ্রাফ করা হয়েছে যা সর্বনিম্ন ক্ষতি করে।
এই ডেটাসেটের জন্য এটি সেরা মডেল হবে কারণ অন্য কোন ওজন এবং পক্ষপাতের মান কম ক্ষতি সহ একটি মডেল তৈরি করে না।
