梯度下降法是一种数学技巧,可迭代地找到能使模型产生最低损失的权重和偏差。梯度下降法通过重复以下过程(迭代次数由用户定义)来找到最佳权重和偏差。
模型开始训练时,权重和偏差会随机化为接近于零的值,然后重复执行以下步骤:
使用当前权重和偏差计算损失。
确定可减少损失的权重和偏差移动方向。
将权重和偏差值沿可减少损失的方向移动少量距离。
返回到第 1 步,重复此过程,直到模型无法进一步减少损失为止。
下图概述了梯度下降法为找到可生成损失最低的模型的权重和偏差而执行的迭代步骤。
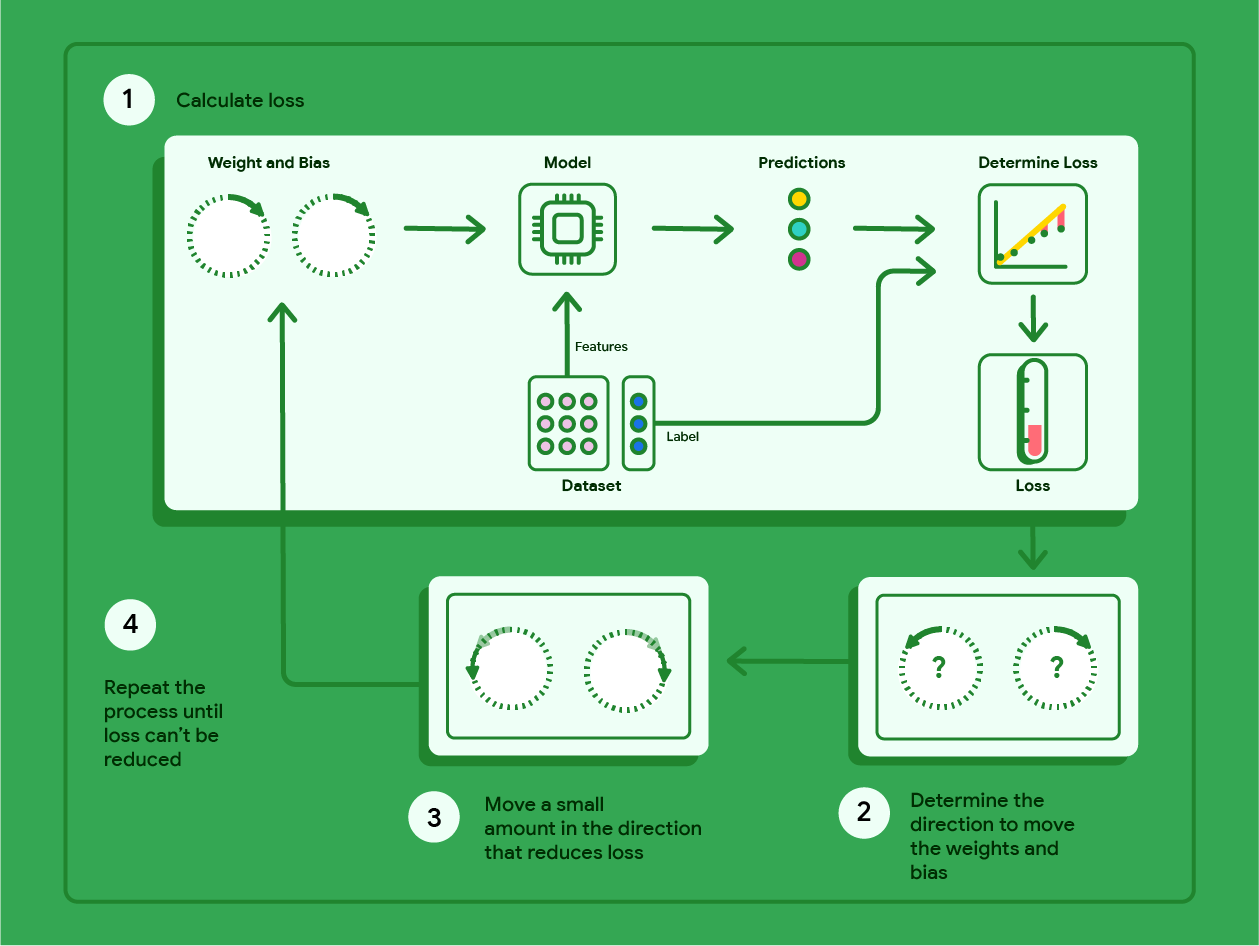
图 11. 梯度下降法是一种迭代过程,用于查找可生成损失最低的模型的权重和偏差。
点击加号图标,详细了解梯度下降法背后的数学原理。
在具体层面上,我们可以使用以下包含 7 个示例的小型燃油效率数据集,并以
均方误差 (MSE) 作为损失指标,逐步完成梯度下降法:
| 以千为单位的磅数(功能) |
每加仑燃油行驶的英里数(标签) |
| 3.5 |
18 |
| 3.69 |
15 |
| 3.44 |
18 |
| 3.43 |
16 |
| 4.34 |
15 |
| 4.42 |
14 |
| 2.37 |
24 |
-
模型通过将权重和偏差设置为零来开始训练:
$$ \small{Weight:\ 0} $$
$$ \small{Bias:\ 0} $$
$$ \small{y = 0 + 0(x_1)} $$
-
使用当前模型参数计算 MSE 损失:
$$ \small{Loss = \frac{(18-0)^2 + (15-0)^2 + (18-0)^2 + (16-0)^2 + (15-0)^2 + (14-0)^2 + (24-0)^2}{7}} $$
$$ \small{Loss= 303.71} $$
-
计算每个权重和偏置处损失函数的切线的斜率:
$$ \small{Weight\ slope: -119.7} $$
$$ \small{Bias\ slope: -34.3} $$
点击加号图标,了解如何计算斜率。
为了获得与权重和偏差相切的直线的斜率,我们对损失函数相对于权重和偏差求导,然后求解方程。
我们将预测方程写为:
$ f_{w,b}(x) = (w*x)+b $。
我们将实际值写为:$y$。
我们将使用以下公式计算 MSE:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
其中,$i$ 表示第 $i$ 个训练样本,$M$ 表示样本数量。
权重导数
损失函数相对于权重的导数可写为:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
并计算出以下结果:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
首先,我们将每个预测值减去实际值,然后将其乘以特征值的两倍。
然后,我们将总和除以示例数量。
结果是与权重值相切的直线的斜率。
如果我们求解此方程,并将权重和偏差设为零,则会得到 -119.7 的直线斜率。
偏差导数
损失函数相对于偏差的导数可写为:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
并计算得出:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
首先,我们计算每个预测值与实际值之差的总和,然后将其乘以 2。然后,我们将总和除以样本数量。结果是与偏差值相切的直线的斜率。
如果我们求解此方程,并将权重和偏差设为零,则会得到 -34.3 的直线斜率。
-
沿负斜率方向移动少量距离,即可得到下一个权重和偏差。目前,我们将任意定义“少量”为 0.01:
$$ \small{New\ weight = old\ weight - (small\ amount * weight\ slope)} $$
$$ \small{New\ bias = old\ bias - (small\ amount * bias\ slope)} $$
$$ \small{New\ weight = 0 - (0.01)*(-119.7)} $$
$$ \small{New\ bias = 0 - (0.01)*(-34.3)} $$
$$ \small{New\ weight = 1.2} $$
$$ \small{New\ bias = 0.34} $$
使用新的权重和偏差计算损失并重复此过程。完成六次迭代后,我们将获得以下权重、偏差和损失:
| 迭代 |
重量 |
偏见 |
损失(均方误差) |
| 1 |
0 |
0 |
303.71 |
| 2 |
1.20 |
0.34 |
170.84 |
| 3 |
2.05 |
0.59 |
103.17 |
| 4 |
2.66 |
0.78 |
68.70 |
| 5 |
3.09 |
0.91 |
51.13 |
| 6 |
3.40 |
1.01 |
42.17 |
您可以看到,随着每次更新权重和偏差,损失会越来越低。
在此示例中,我们在 6 次迭代后停止了训练。实际上,模型会一直训练,直到收敛为止。
当模型收敛时,额外的迭代不会进一步减少损失,因为梯度下降法已经找到了可将损失降至最低的权重和偏差。
如果模型在收敛后继续训练,损失会开始小幅波动,因为模型会不断更新参数,使其接近最低值。这可能会导致难以验证模型是否已实际收敛。如需确认模型是否已收敛,您需要继续训练,直到损失趋于稳定。
模型收敛和损失曲线
在训练模型时,您通常会查看损失曲线,以确定模型是否已收敛。损失曲线显示了损失随模型训练的变化情况。下图显示了典型的损失曲线。y 轴表示损失,x 轴表示迭代次数:
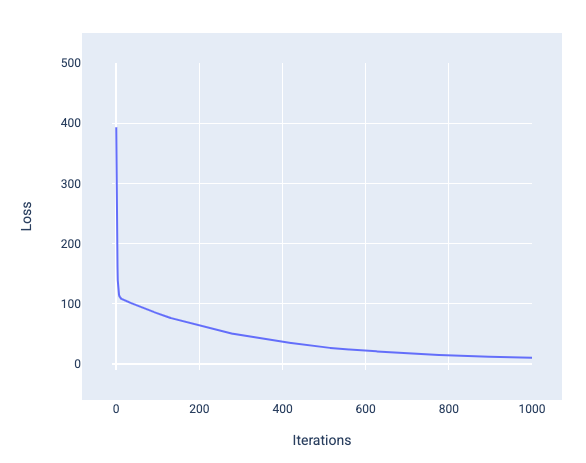
图 12. 损失曲线,显示模型在第 1,000 次迭代左右收敛。
您可以看到,在前几次迭代中,损失大幅减少,然后逐渐减少,在第 1,000 次迭代左右趋于平缓。经过 1,000 次迭代后,我们基本上可以确定模型已收敛。
在下图中,我们绘制了模型在训练过程中的三个时间点(开始、中间和结束)的状态。直观呈现训练过程中快照的模型状态,可巩固权重和偏差更新、损失减少与模型收敛之间的联系。
在图中,我们使用特定迭代次数时得出的权重和偏差来表示模型。在包含数据点和模型快照的图中,从模型到数据点的蓝色损失线表示损失量。线条越长,损失越大。
在下图中,我们可以看到,在第二次迭代左右,由于损失过大,模型将无法很好地进行预测。
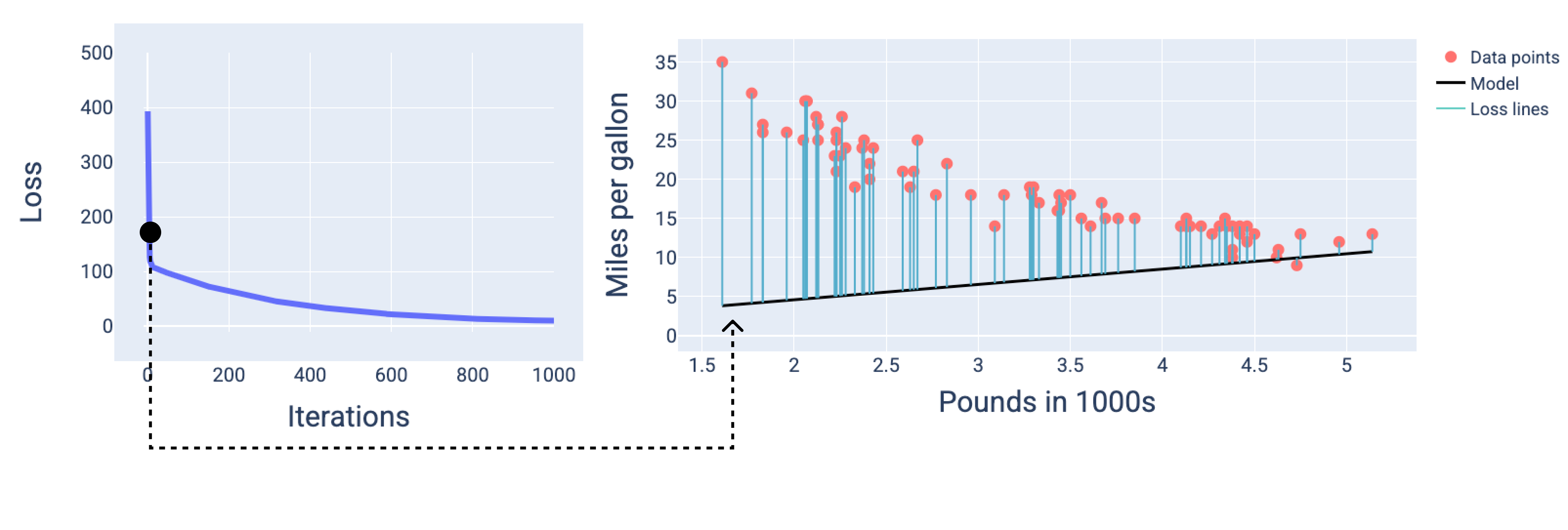
图 13. 训练过程开始时的损失曲线和模型快照。
在大约第 400 次迭代时,我们可以看到梯度下降法已经找到了能够生成更好模型的权重和偏差。
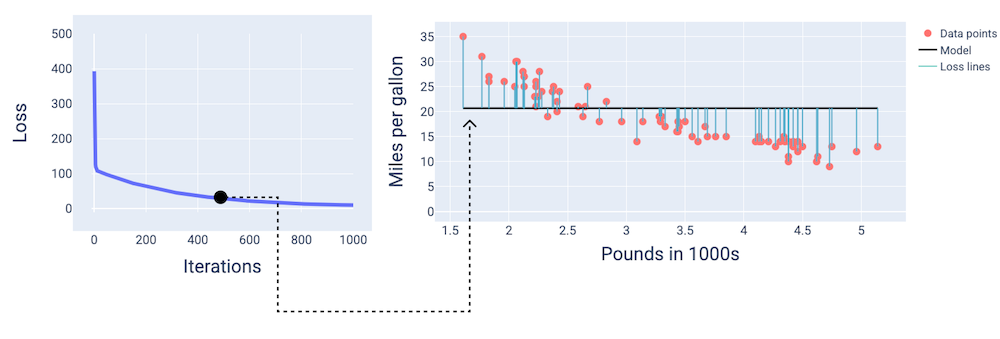
图 14. 损失曲线和训练中途的模型快照。
在大约第 1,000 次迭代时,我们可以看到模型已经收敛,生成了损失尽可能最低的模型。
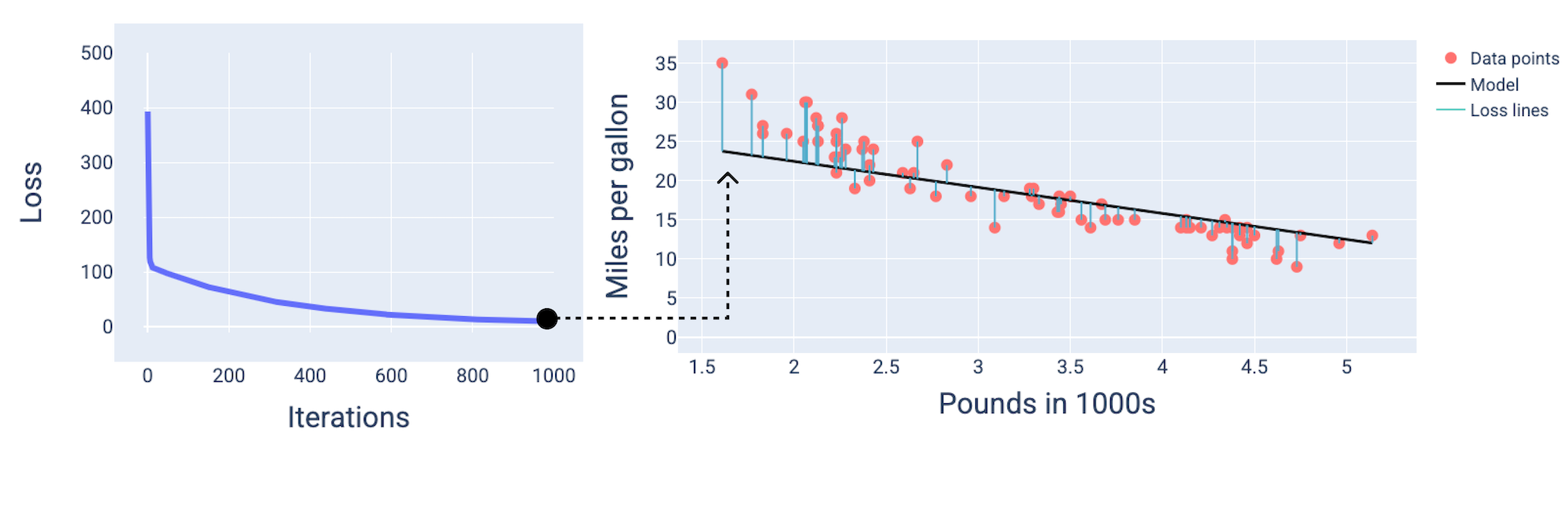
图 15. 训练过程接近结束时的损失曲线和模型快照。
练习:检查您的理解情况
梯度下降法在线性回归中的作用是什么?
梯度下降法是一种迭代过程,可找到能最大限度减少损失的最佳权重和偏差。
梯度下降法有助于确定在训练模型时使用哪种类型的损失,例如 L1 或 L2。
梯度下降法不涉及模型训练的损失函数选择。
梯度下降法会从数据集中移除离群值,以帮助模型做出更好的预测。
梯度下降法不会更改数据集。
收敛和凸函数
线性模型的损失函数始终会生成凸面。根据这一属性,当线性回归模型收敛时,我们知道该模型已找到可产生最低损失的权重和偏差。
如果我们绘制具有一个特征的模型的损失曲面图,可以看到其凸形。下图显示了假设的每加仑英里数数据集的损失曲面。权重位于 x 轴上,偏差位于 y 轴上,损失位于 z 轴上:
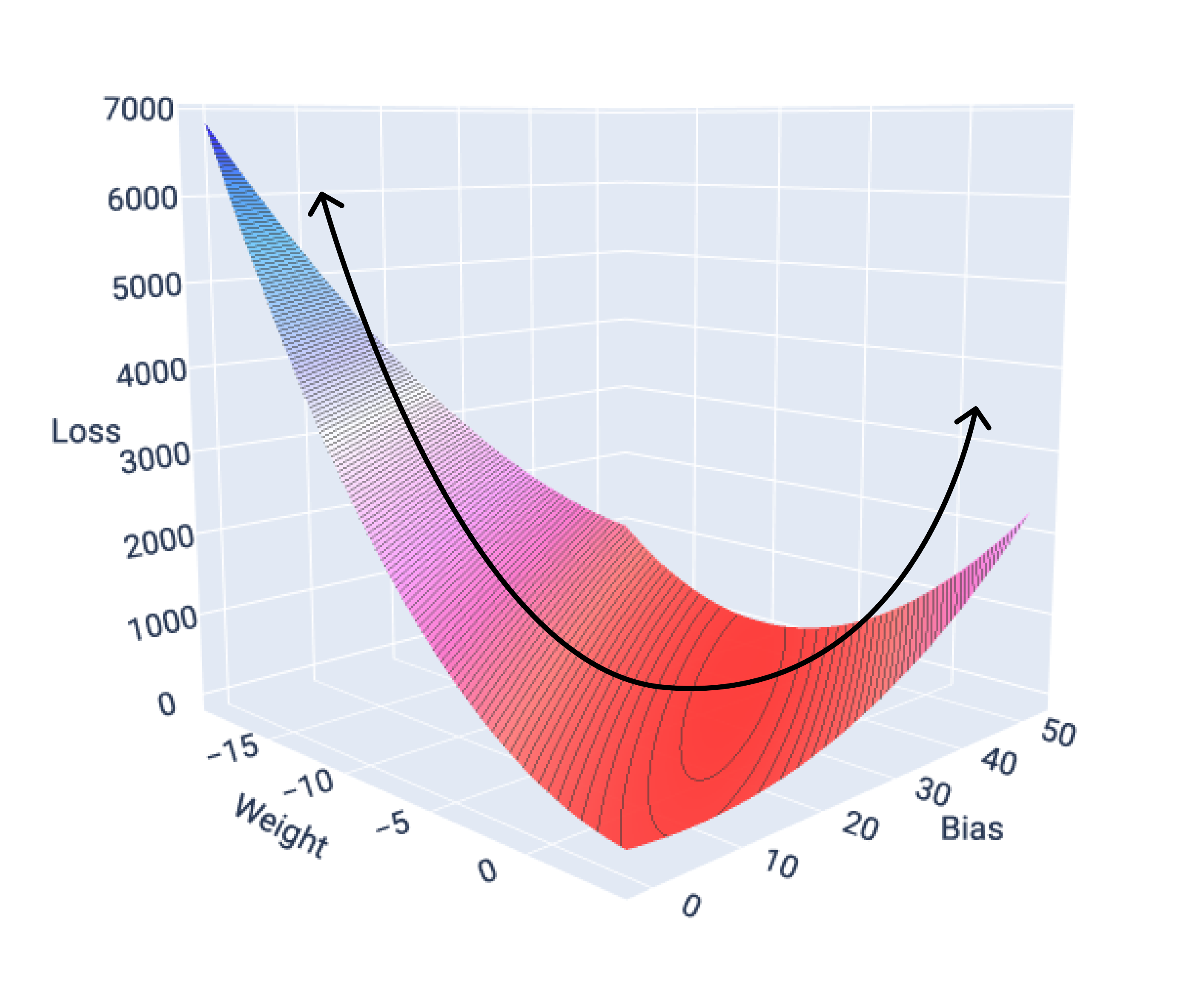
图 16. 显示凸形的损失曲面。
在此示例中,权重为 -5.44,偏差为 35.94,可产生最低的损失值 5.54:
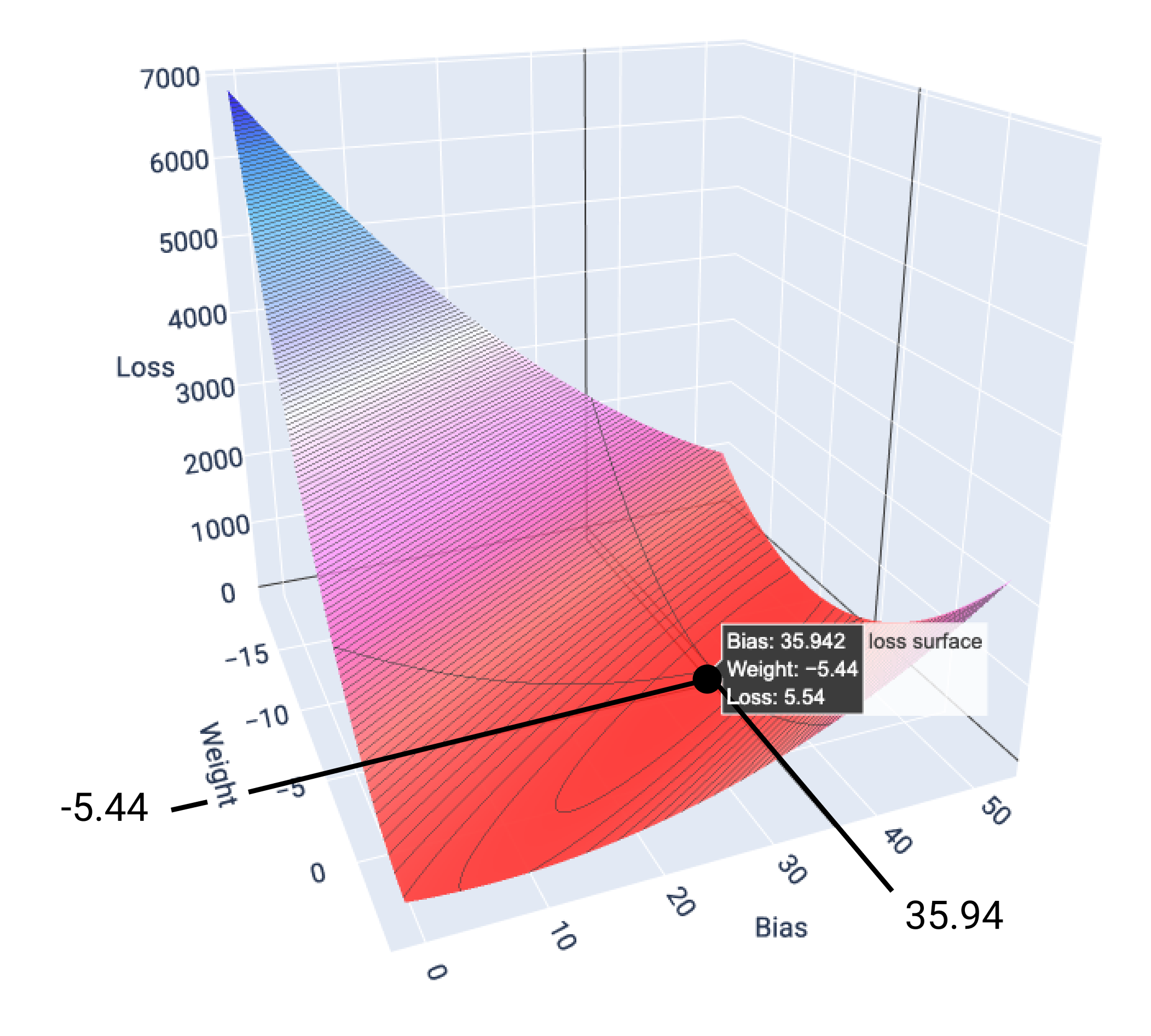
图 17. 显示产生最低损失的权重和偏差值的损失曲面。
当线性模型找到最小损失时,它会收敛。如果我们绘制梯度下降法期间的权重和偏差点图,这些点看起来就像一个球从山上滚下来,最终停在没有更多向下坡度的点。
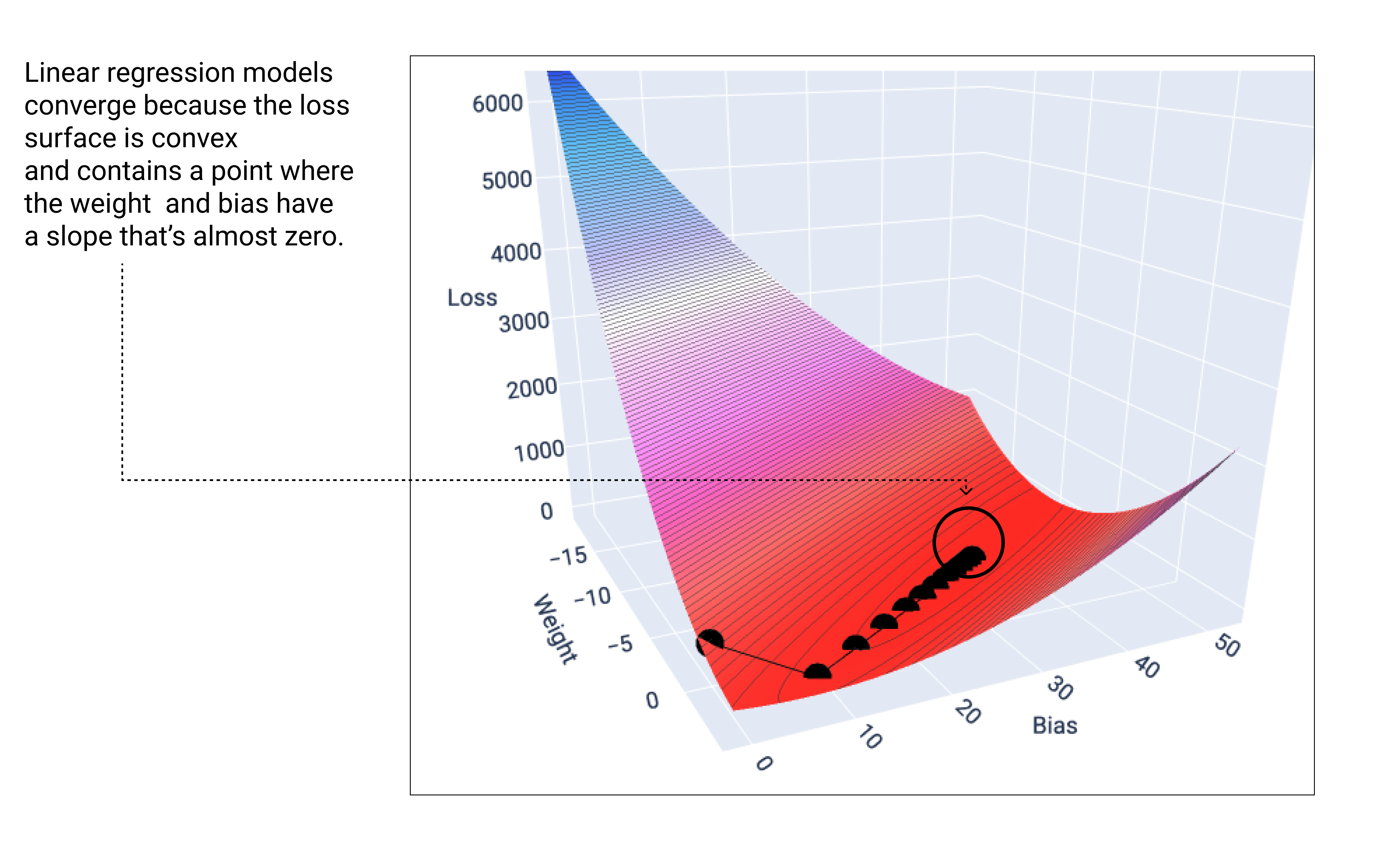
图 18. 损失图,显示了梯度下降点停止在图表最低点的情况。
请注意,黑色损失点会形成损失曲线的确切形状:先是急剧下降,然后逐渐向下倾斜,直到达到损失曲面上的最低点。
使用产生最低损失的权重和偏差值(在本例中,权重为 -5.44,偏差为 35.94),我们可以绘制模型图,看看它与数据的拟合程度如何:
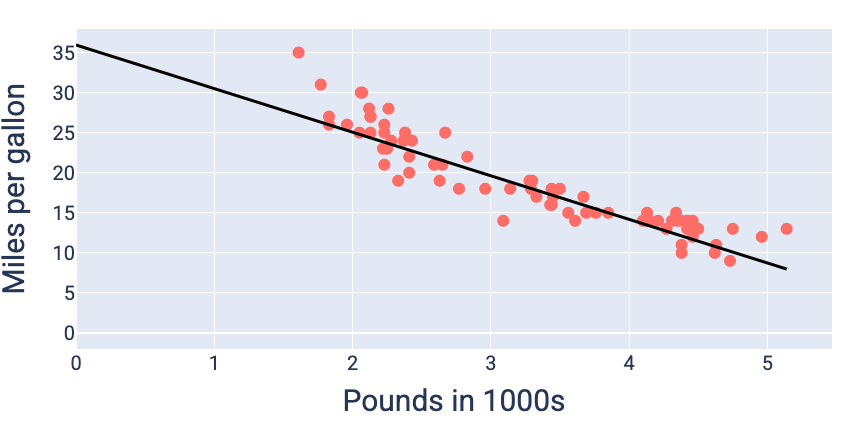
图 19. 使用产生最低损失的权重和偏差值绘制的模型图。
对于此数据集,这将是最佳模型,因为没有其他权重和偏差值能生成损失更低的模型。








