Penurunan gradien adalah teknik matematika yang secara berulang menemukan bobot dan bias yang menghasilkan model dengan kerugian terendah. Gradient descent menemukan bobot dan bias terbaik dengan mengulangi proses berikut untuk sejumlah iterasi yang ditentukan pengguna.
Model memulai pelatihan dengan bobot dan bias acak mendekati nol, lalu mengulangi langkah-langkah berikut:
Hitung kerugian dengan bobot dan bias saat ini.
Tentukan arah untuk memindahkan bobot dan bias yang mengurangi kerugian.
Pindahkan nilai bobot dan bias dalam jumlah kecil ke arah yang mengurangi kerugian.
Kembali ke langkah pertama dan ulangi prosesnya hingga model tidak dapat mengurangi kerugian lebih lanjut.
Diagram di bawah menguraikan langkah-langkah iteratif yang dilakukan penurunan gradien untuk menemukan bobot dan bias yang menghasilkan model dengan kerugian terendah.
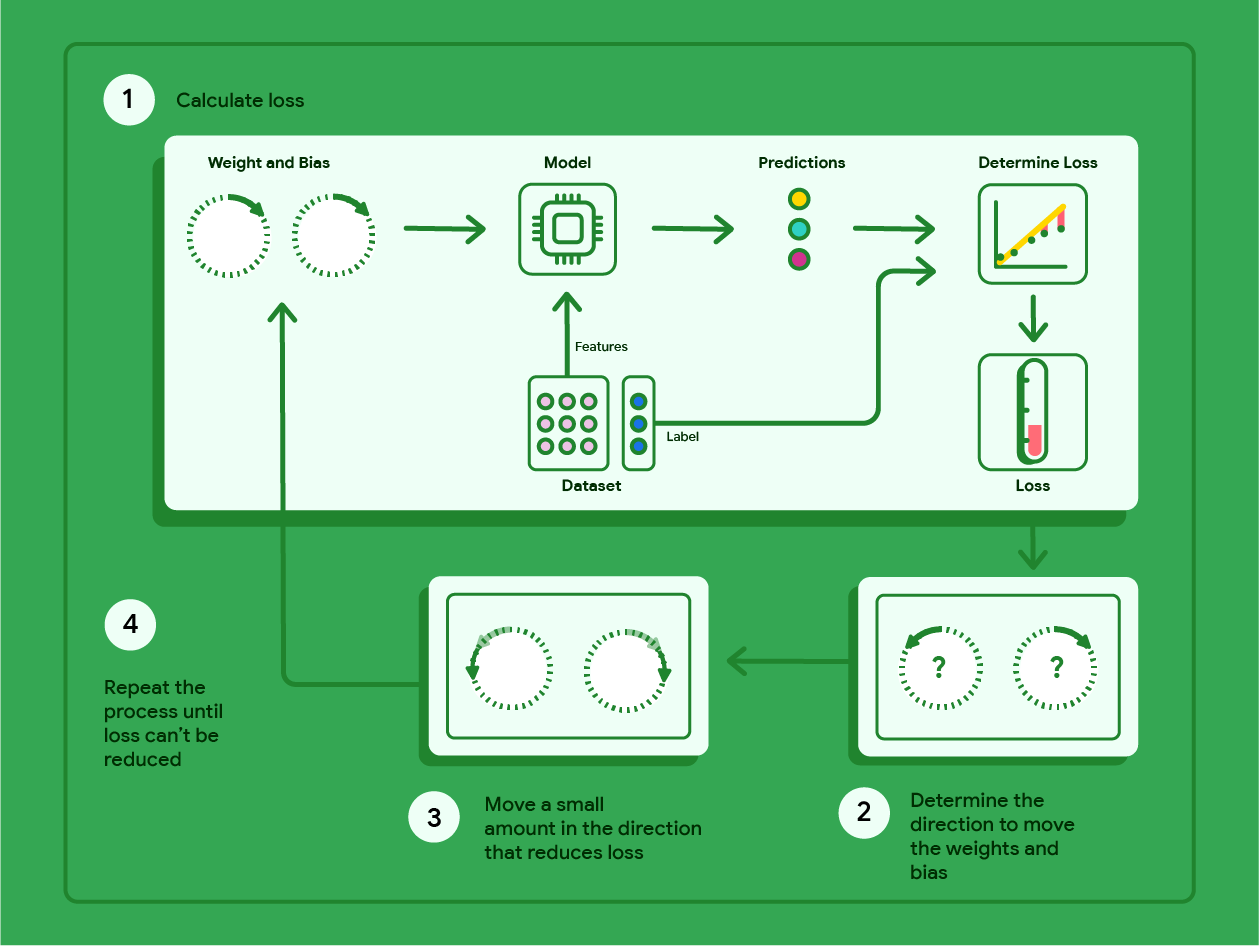
Gambar 11. Penurunan gradien adalah proses iteratif yang menemukan bobot dan bias yang menghasilkan model dengan kerugian terendah.
Klik ikon plus untuk mempelajari lebih lanjut matematika di balik penurunan gradien.
Pada tingkat yang konkret, kita dapat mempelajari langkah-langkah penurunan gradien menggunakan set data kecil dengan tujuh contoh untuk berat mobil dalam pound dan rating mil per galonnya:
| Pound dalam ribuan (fitur) | Mil per galon (label) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
- Model memulai pelatihan dengan menyetel bobot dan bias ke nol:
- Hitung kerugian MSE dengan parameter model saat ini:
- Hitung kemiringan garis singgung terhadap fungsi kerugian pada setiap bobot dan bias:
- Pindahkan sedikit ke arah kemiringan negatif untuk mendapatkan bobot dan bias berikutnya. Untuk saat ini, kita akan mendefinisikan "jumlah kecil" sebagai 0,01:
Klik ikon plus untuk mempelajari cara menghitung kemiringan.
Untuk mendapatkan kemiringan garis yang bersinggungan dengan bobot dan bias, kita mengambil turunan fungsi kerugian sehubungan dengan bobot dan bias, lalu menyelesaikan persamaan.
Kita akan menulis persamaan untuk membuat prediksi sebagai:
$ f_{w,b}(x) = (w*x)+b $.
Kita akan menulis nilai sebenarnya sebagai: $ y $.
Kita akan menghitung MSE menggunakan:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
dengan $i$ mewakili contoh pelatihan ke-$ith$ dan $M$ mewakili
jumlah contoh.
Turunan fungsi kerugian terhadap bobot ditulis sebagai:
$ \frac{\partial }{\partial w} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
dan dievaluasi menjadi:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2x_{(i)} $
Pertama, kita menjumlahkan setiap nilai prediksi dikurangi nilai sebenarnya lalu mengalikannya dengan dua kali nilai fitur. Kemudian, kita membagi jumlah tersebut dengan jumlah contoh. Hasilnya adalah kemiringan garis tangen terhadap nilai bobot.
Jika kita menyelesaikan persamaan ini dengan bobot dan bias yang sama dengan nol, kita akan mendapatkan -119,7 untuk kemiringan garis.
Turunan bias
Turunan fungsi kerugian terhadap
bias ditulis sebagai:
$ \frac{\partial }{\partial b} \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)})^2 $
dan dievaluasi menjadi:
$ \frac{1}{M} \sum_{i=1}^{M} (f_{w,b}(x_{(i)}) - y_{(i)}) * 2 $
Pertama, kita menjumlahkan setiap nilai prediksi dikurangi nilai sebenarnya lalu mengalikannya dengan dua. Kemudian, kita membagi jumlah tersebut dengan jumlah contoh. Hasilnya adalah kemiringan garis tangen terhadap nilai bias.
Jika kita menyelesaikan persamaan ini dengan bobot dan bias yang sama dengan nol, kita akan mendapatkan -34,3 untuk kemiringan garis.
Gunakan bobot dan bias baru untuk menghitung kerugian dan pengulangan. Setelah menyelesaikan proses selama enam iterasi, kita akan mendapatkan bobot, bias, dan kerugian berikut:
| Iterasi | Berat | Bias | Kerugian (MSE) |
|---|---|---|---|
| 1 | 0 | 0 | 303.71 |
| 2 | 1,20 | 0,34 | 170.84 |
| 3 | 2,05 | 0,59 | 103,17 |
| 4 | 2,66 | 0,78 | 68.70 |
| 5 | 3,09 | 0,91 | 51.13 |
| 6 | 3,40 | 1.01 | 42,17 |
Anda dapat melihat bahwa kerugian semakin kecil dengan setiap bobot dan bias yang diperbarui. Dalam contoh ini, kita berhenti setelah enam iterasi. Dalam praktiknya, model dilatih hingga berkonvergensi. Saat model menyatu, iterasi tambahan tidak mengurangi kerugian lebih lanjut karena penurunan gradien telah menemukan bobot dan bias yang hampir meminimalkan kerugian.
Jika model terus dilatih setelah konvergensi, kerugian akan mulai berfluktuasi dalam jumlah kecil karena model terus memperbarui parameter di sekitar nilai terendahnya. Hal ini dapat menyulitkan verifikasi bahwa model telah benar-benar konvergen. Untuk mengonfirmasi bahwa model telah konvergen, Anda harus melanjutkan pelatihan hingga kerugian stabil.
Konvergensi model dan kurva kerugian
Saat melatih model, Anda sering kali melihat kurva kerugian untuk menentukan apakah model telah berkonvergensi. Kurva kerugian menunjukkan bagaimana perubahan kerugian saat model dilatih. Berikut adalah tampilan kurva kerugian umum. Kerugian berada pada sumbu y dan iterasi berada pada sumbu x:
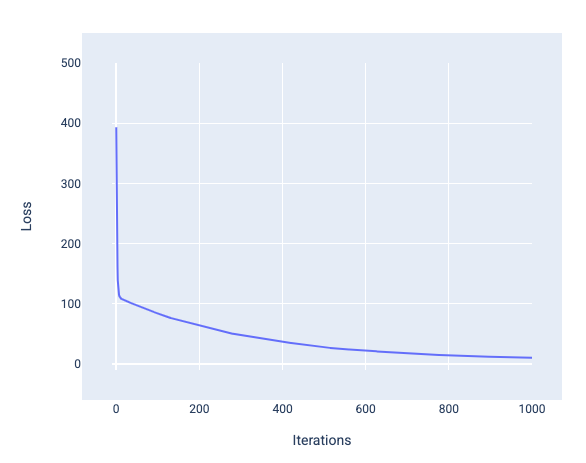
Gambar 12. Kurva kerugian yang menunjukkan model menyatu di sekitar tanda iterasi ke-1.000.
Anda dapat melihat bahwa kerugian menurun secara drastis selama beberapa iterasi pertama, kemudian menurun secara bertahap sebelum stabil di sekitar iterasi ke-1.000. Setelah 1.000 iterasi, kita dapat memastikan bahwa model telah berkonvergensi.
Pada gambar berikut, kita menggambarkan model pada tiga titik selama proses pelatihan: awal, tengah, dan akhir. Memvisualisasikan status model pada snapshot selama proses pelatihan memperkuat hubungan antara memperbarui bobot dan bias, mengurangi kerugian, dan konvergensi model.
Dalam gambar, kita menggunakan bobot dan bias yang diperoleh pada iterasi tertentu untuk merepresentasikan model. Dalam grafik dengan titik data dan snapshot model, garis kerugian biru dari model ke titik data menunjukkan jumlah kerugian. Semakin panjang garis, semakin besar kerugiannya.
Pada gambar berikut, kita dapat melihat bahwa sekitar iterasi kedua, model tidak akan dapat membuat prediksi dengan baik karena jumlah kerugian yang tinggi.
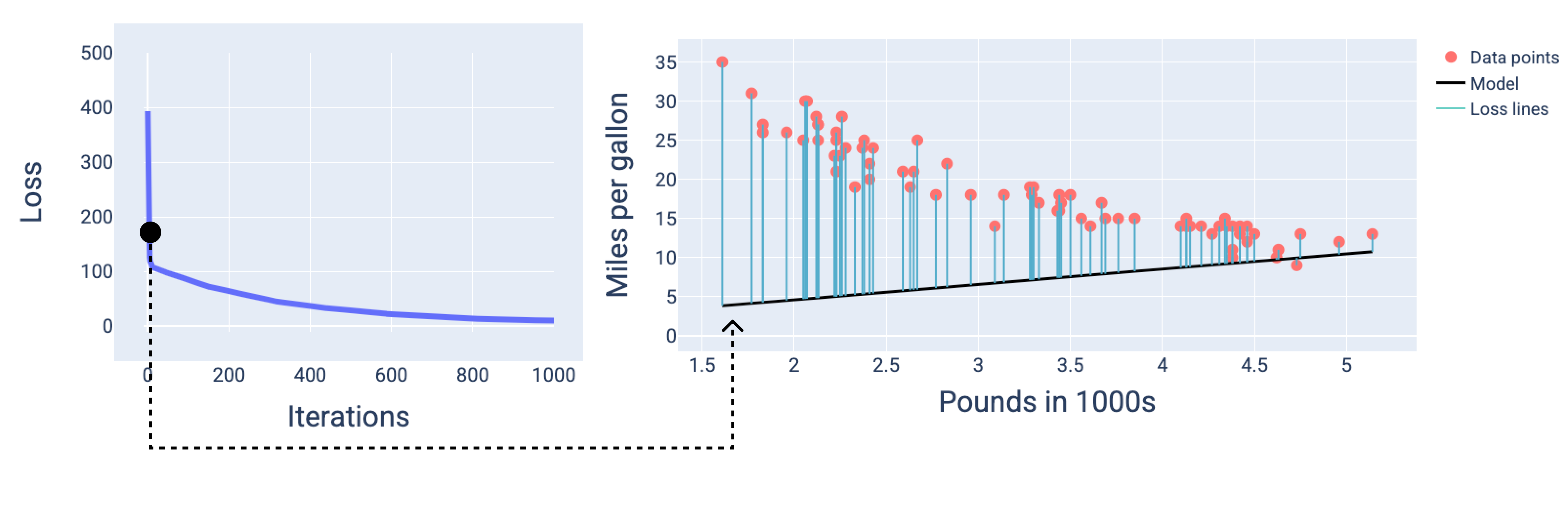
Gambar 13. Kurva kerugian dan snapshot model di awal proses pelatihan.
Pada iterasi ke-400, kita dapat melihat bahwa penurunan gradien telah menemukan bobot dan bias yang menghasilkan model yang lebih baik.
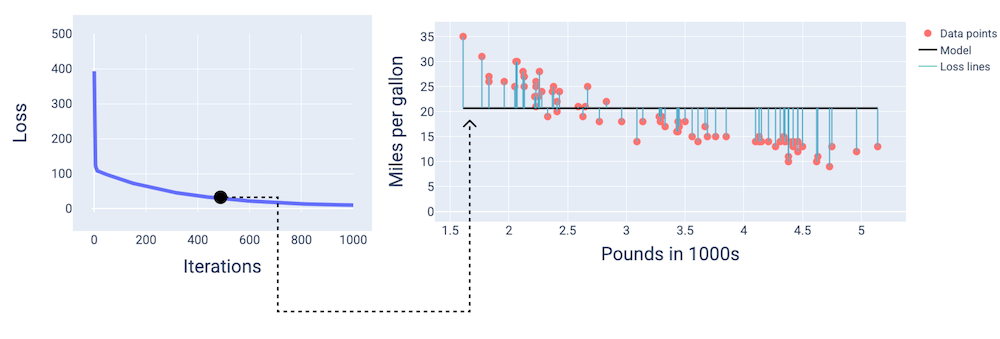
Gambar 14. Kurva kerugian dan snapshot model di tengah pelatihan.
Dan pada iterasi ke-1.000, kita dapat melihat bahwa model telah menyatu, menghasilkan model dengan kerugian serendah mungkin.
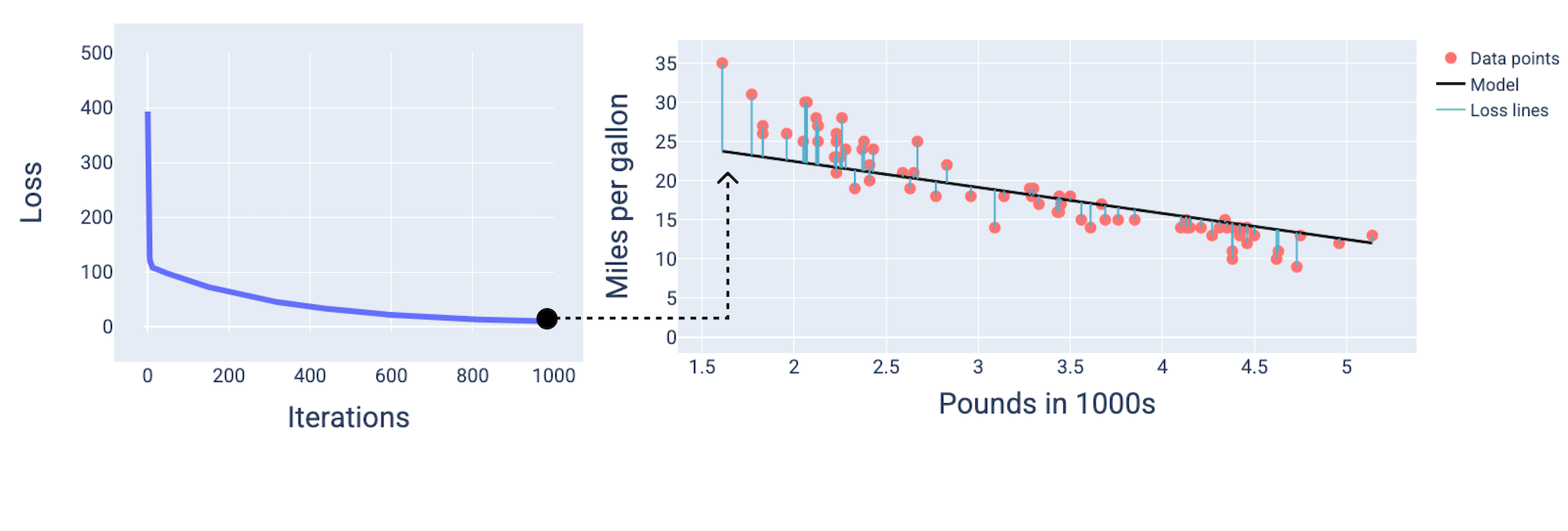
Gambar 15. Kurva kerugian dan ringkasan model menjelang akhir proses pelatihan.
Latihan: Periksa pemahaman Anda
Konvergensi dan fungsi konveks
Fungsi kerugian untuk model linear selalu menghasilkan permukaan konveks. Sebagai hasil dari properti ini, saat model regresi linear konvergen, kita tahu bahwa model telah menemukan bobot dan bias yang menghasilkan kerugian terendah.
Jika kita membuat grafik permukaan kerugian untuk model dengan satu fitur, kita dapat melihat bentuk cembungnya. Berikut adalah permukaan kerugian untuk set data mil per galon hipotetis. Bobot berada pada sumbu x, bias berada pada sumbu y, dan kerugian berada pada sumbu z:
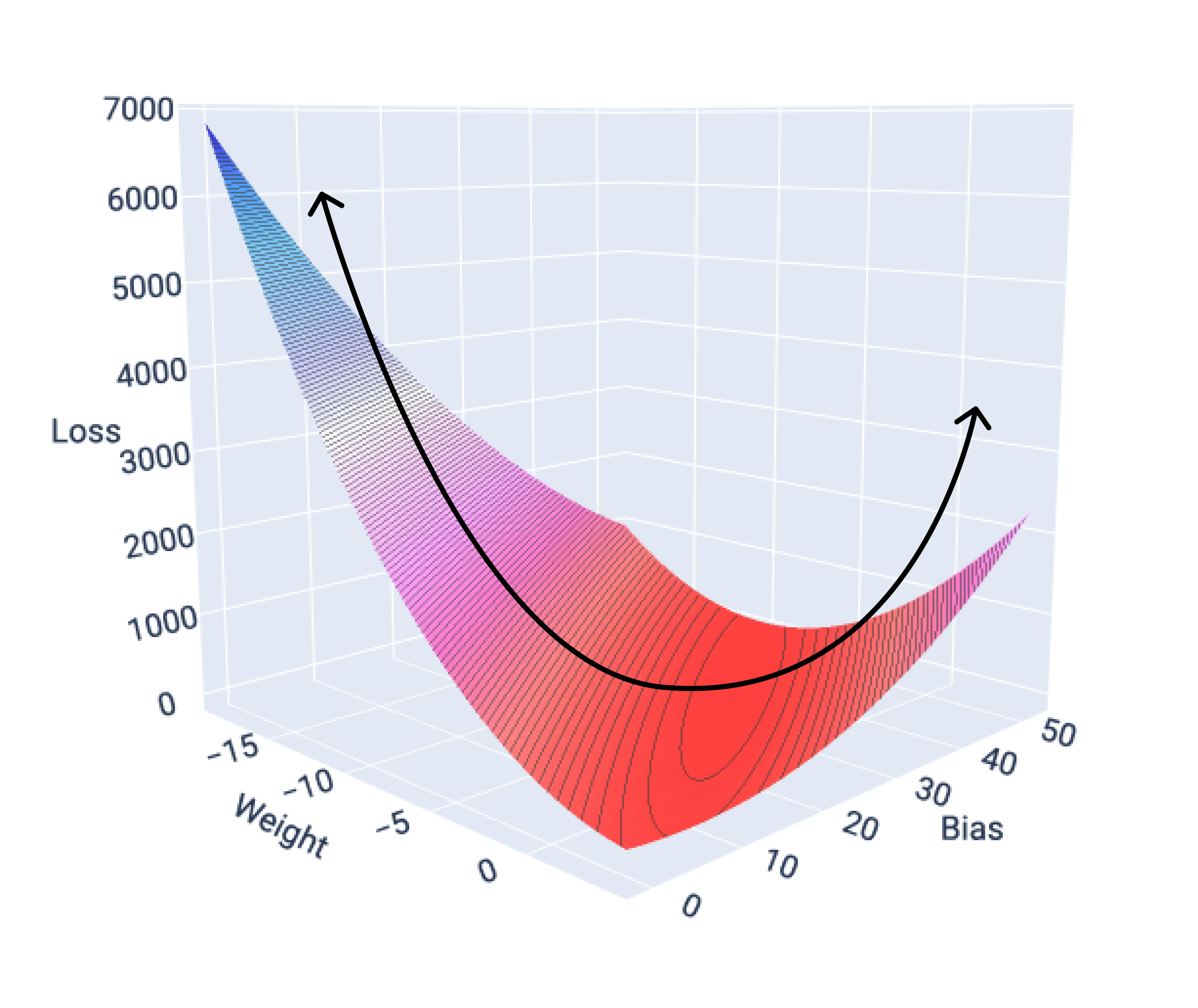
Gambar 16. Permukaan kerugian yang menunjukkan bentuk cembungnya.
Dalam contoh ini, bobot -5,44 dan bias 35,94 menghasilkan kerugian terendah pada 5,54:
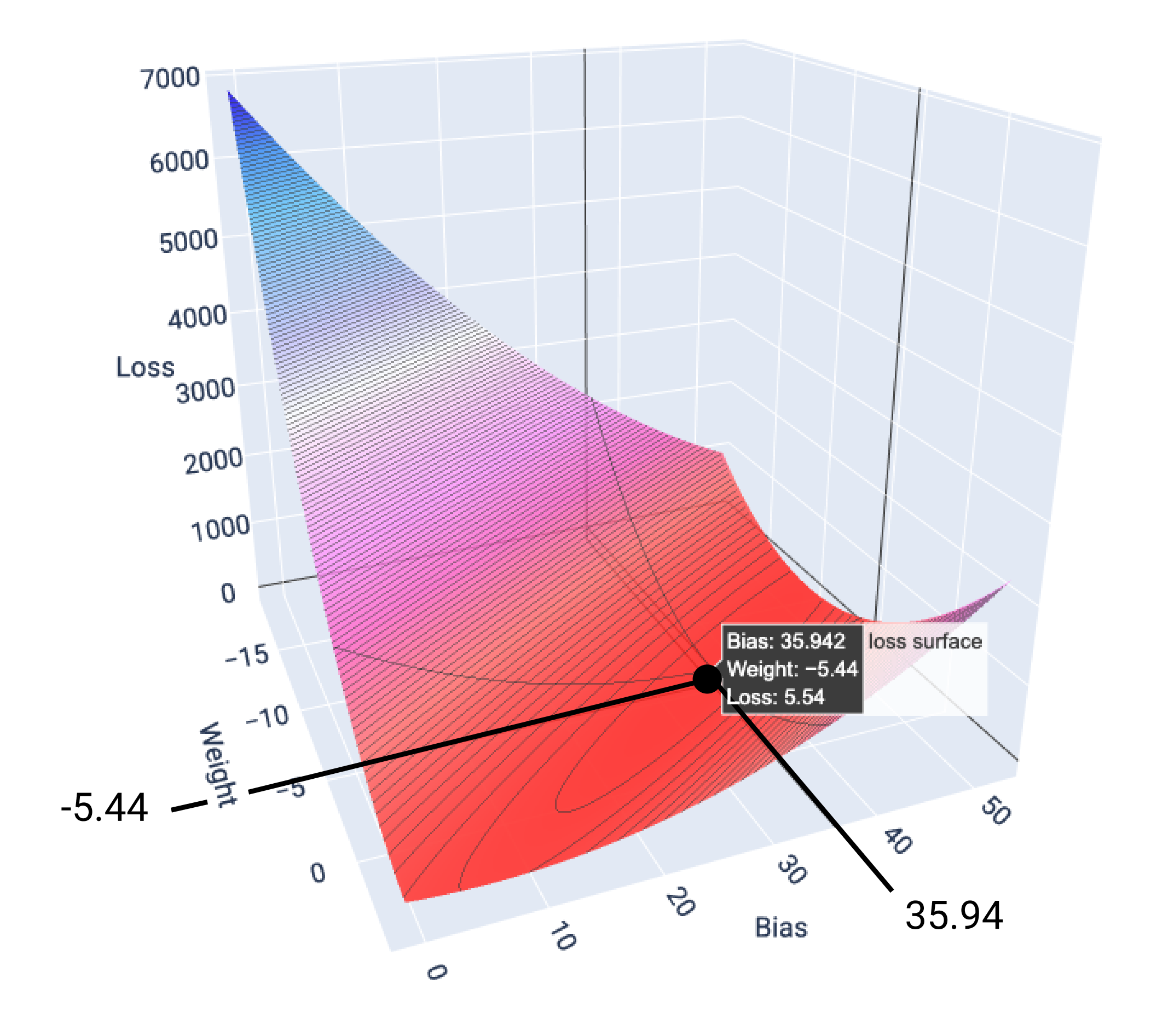
Gambar 17. Permukaan kerugian yang menunjukkan nilai bobot dan bias yang menghasilkan kerugian terendah.
Model linear akan konvergen saat menemukan kehilangan minimum. Oleh karena itu, iterasi tambahan hanya menyebabkan penurunan gradien memindahkan nilai bobot dan bias dalam jumlah yang sangat kecil di sekitar minimum. Jika kita memetakan titik bobot dan bias selama penurunan gradien, titik-titik tersebut akan terlihat seperti bola yang menggelinding menuruni bukit, dan akhirnya berhenti di titik yang tidak memiliki lagi kemiringan ke bawah.
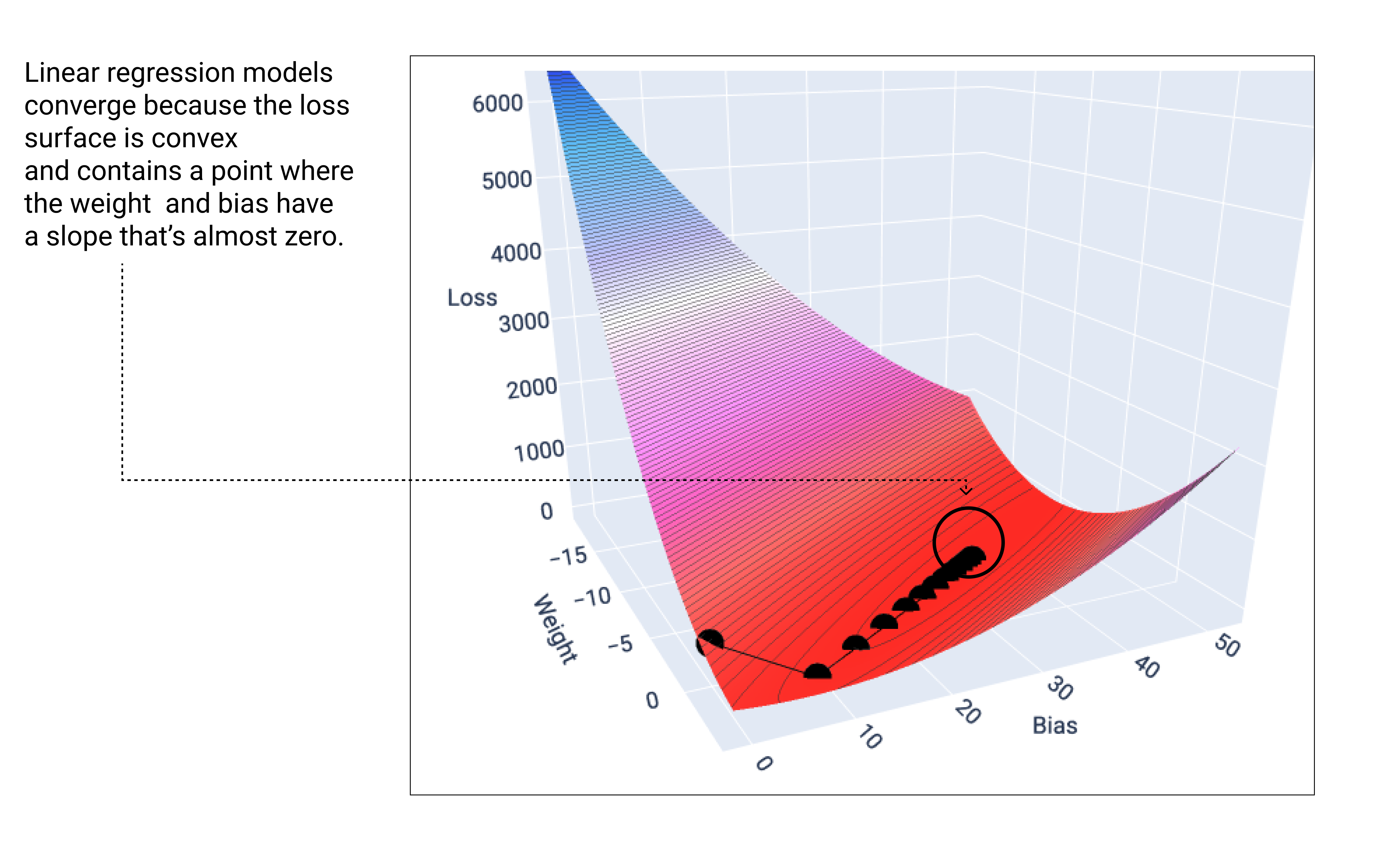
Gambar 18. Grafik kerugian yang menunjukkan titik penurunan gradien berhenti di titik terendah pada grafik.
Perhatikan bahwa titik kerugian hitam membentuk bentuk kurva kerugian yang persis sama: penurunan tajam sebelum menurun secara bertahap hingga mencapai titik terendah pada permukaan kerugian.
Perlu diperhatikan bahwa model hampir tidak pernah menemukan nilai minimum yang tepat untuk setiap bobot dan bias, tetapi menemukan nilai yang sangat mendekati. Penting juga untuk diperhatikan bahwa nilai minimum untuk bobot dan bias tidak sesuai dengan kehilangan nol, hanya nilai yang menghasilkan kehilangan terendah untuk parameter tersebut.
Dengan menggunakan nilai bobot dan bias yang menghasilkan kerugian terkecil—dalam hal ini bobot -5,44 dan bias 35,94—kita dapat membuat grafik model untuk melihat seberapa baik kecocokannya dengan data:
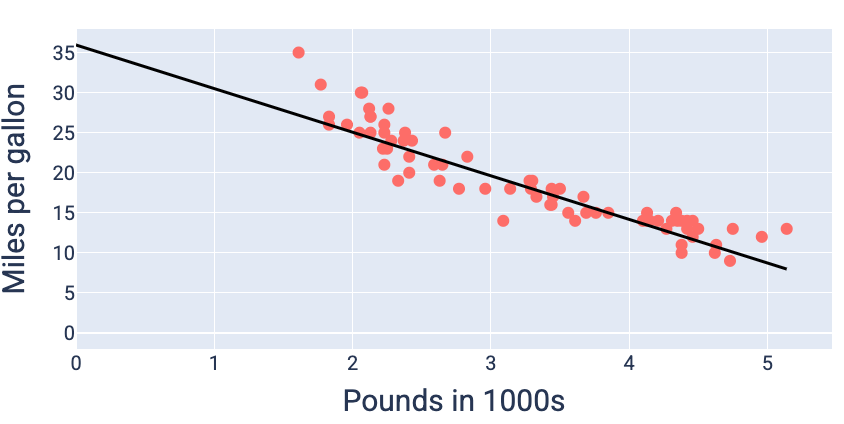
Gambar 19. Model yang di-plotting menggunakan nilai bobot dan bias yang menghasilkan kerugian terendah.
Ini akan menjadi model terbaik untuk set data ini karena tidak ada nilai bobot dan bias lain yang menghasilkan model dengan kerugian yang lebih rendah.
