Los hiperparámetros son variables que controlan diferentes aspectos del entrenamiento. Tres hiperparámetros comunes son los siguientes:
En cambio, los parámetros son las variables, como los pesos y la ordenada al origen, que forman parte del modelo en sí. En otras palabras, los hiperparámetros son valores que controlas, mientras que los parámetros son valores que el modelo calcula durante el entrenamiento.
Tasa de aprendizaje
La tasa de aprendizaje es un número de punto flotante que estableces y que influye en la rapidez con la que converge el modelo. Si la tasa de aprendizaje es demasiado baja, el modelo puede tardar mucho en converger. Sin embargo, si la tasa de aprendizaje es demasiado alta, el modelo nunca converge, sino que oscila entre los pesos y la ordenada al origen que minimizan la pérdida. El objetivo es elegir una tasa de aprendizaje que no sea demasiado alta ni demasiado baja para que el modelo converja rápidamente.
La tasa de aprendizaje determina la magnitud de los cambios que se deben realizar en los pesos y el sesgo durante cada paso del proceso de descenso de gradientes. El modelo multiplica el gradiente por la tasa de aprendizaje para determinar los parámetros del modelo (valores de peso y sesgo) para la siguiente iteración. En el tercer paso del descenso del gradiente, la "pequeña cantidad" que se debe mover en la dirección de la pendiente negativa se refiere a la tasa de aprendizaje.
La diferencia entre los parámetros del modelo anterior y los del modelo nuevo es proporcional a la pendiente de la función de pérdida. Por ejemplo, si la pendiente es grande, el modelo da un paso grande. Si es pequeño, da un paso pequeño. Por ejemplo, si la magnitud del gradiente es 2.5 y la tasa de aprendizaje es 0.01, el modelo cambiará el parámetro en 0.025.
La tasa de aprendizaje ideal ayuda al modelo a converger en una cantidad razonable de iteraciones. En la figura 20, la curva de pérdida muestra que el modelo mejora significativamente durante las primeras 20 iteraciones antes de comenzar a converger:
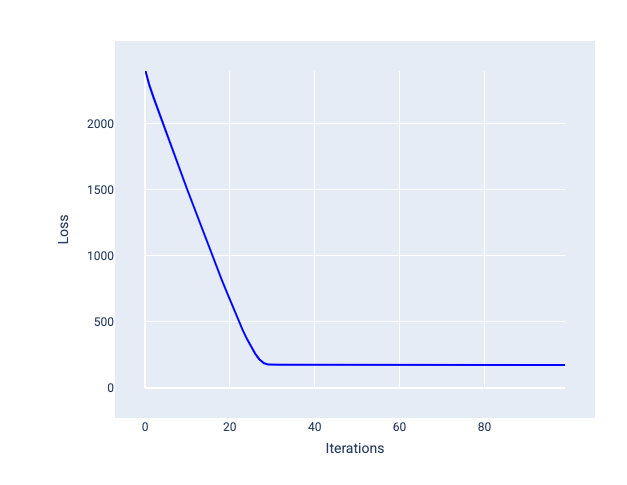
Figura 20: Gráfico de pérdida que muestra un modelo entrenado con una tasa de aprendizaje que converge rápidamente.
Por el contrario, una tasa de aprendizaje demasiado pequeña puede requerir demasiadas iteraciones para converger. En la figura 21, la curva de pérdida muestra que el modelo solo realiza mejoras menores después de cada iteración:
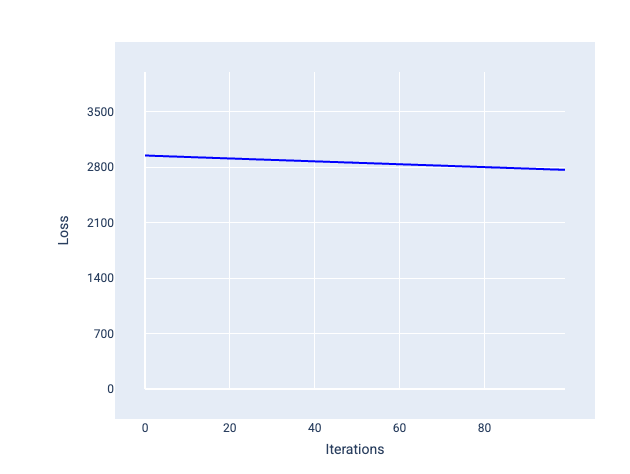
Figura 21. Gráfico de pérdida que muestra un modelo entrenado con una tasa de aprendizaje baja.
Una tasa de aprendizaje demasiado alta nunca converge porque cada iteración hace que la pérdida rebote o aumente continuamente. En la figura 22, la curva de pérdida muestra que el modelo disminuye y, luego, aumenta la pérdida después de cada iteración. En la figura 23, la pérdida aumenta en iteraciones posteriores:
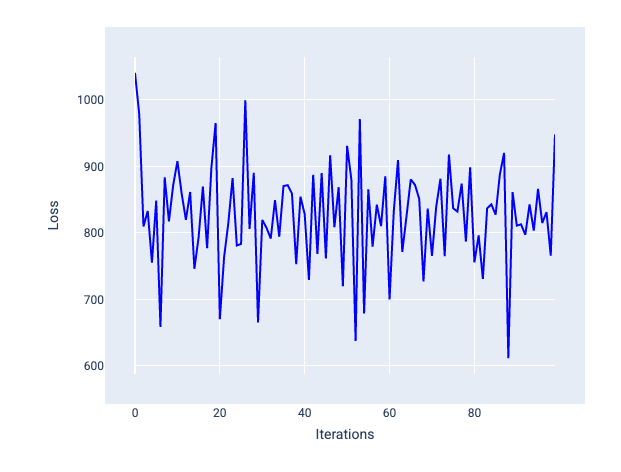
Figura 22: Gráfico de pérdida que muestra un modelo entrenado con una tasa de aprendizaje demasiado alta, en el que la curva de pérdida fluctúa de forma descontrolada, subiendo y bajando a medida que aumentan las iteraciones.
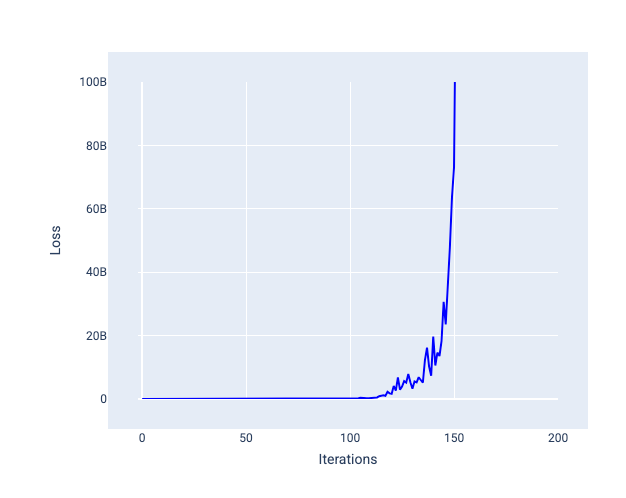
Figura 23. Gráfico de pérdida que muestra un modelo entrenado con una tasa de aprendizaje demasiado alta, en el que la curva de pérdida aumenta drásticamente en iteraciones posteriores.
Ejercicio: Comprueba tus conocimientos
Tamaño del lote
El tamaño del lote es un hiperparámetro que hace referencia a la cantidad de ejemplos que el modelo procesa antes de actualizar sus pesos y sesgos. Es posible que pienses que el modelo debería calcular la pérdida para cada ejemplo del conjunto de datos antes de actualizar los pesos y la desviación. Sin embargo, cuando un conjunto de datos contiene cientos de miles o incluso millones de ejemplos, no es práctico usar el lote completo.
Dos técnicas comunes para obtener el gradiente correcto en promedio sin necesidad de observar cada ejemplo del conjunto de datos antes de actualizar los pesos y la desviación son el descenso de gradiente estocástico y el descenso de gradiente estocástico de minilotes:
Descenso de gradientes estocástico (SGD): El descenso de gradientes estocástico usa solo un ejemplo (un tamaño de lote de uno) por iteración. Cuando se dan demasiadas iteraciones, el SGD funciona, pero es muy ruidoso. El "ruido" hace referencia a las variaciones durante el entrenamiento que hacen que la pérdida aumente en lugar de disminuir durante una iteración. El término "estocástico" indica que el ejemplo que comprende cada lote se elige de forma aleatoria.
En la siguiente imagen, observa cómo la pérdida fluctúa ligeramente a medida que el modelo actualiza sus pesos y sesgos con el método SGD, lo que puede generar ruido en el gráfico de pérdida:
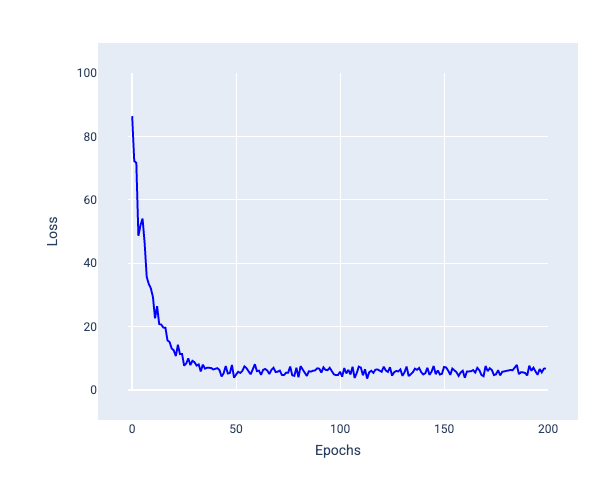
Figura 24. Modelo entrenado con descenso de gradientes estocástico (SGD) que muestra ruido en la curva de pérdida.
Ten en cuenta que el uso del descenso de gradiente estocástico puede generar ruido en toda la curva de pérdida, no solo cerca de la convergencia.
Descenso de gradientes estocástico de minilote (SGD de minilote): El descenso de gradientes estocástico de minilote es un equilibrio entre el lote completo y el SGD. Para una cantidad de $N $ de datos, el tamaño del lote puede ser cualquier número mayor que 1 y menor que $ N $. El modelo elige los ejemplos incluidos en cada lote de forma aleatoria, calcula el promedio de sus gradientes y, luego, actualiza los pesos y el sesgo una vez por iteración.
La determinación de la cantidad de ejemplos para cada lote depende del conjunto de datos y de los recursos de procesamiento disponibles. En general, los tamaños de lotes pequeños se comportan como el SGD, y los tamaños de lotes más grandes se comportan como el descenso del gradiente de lote completo.
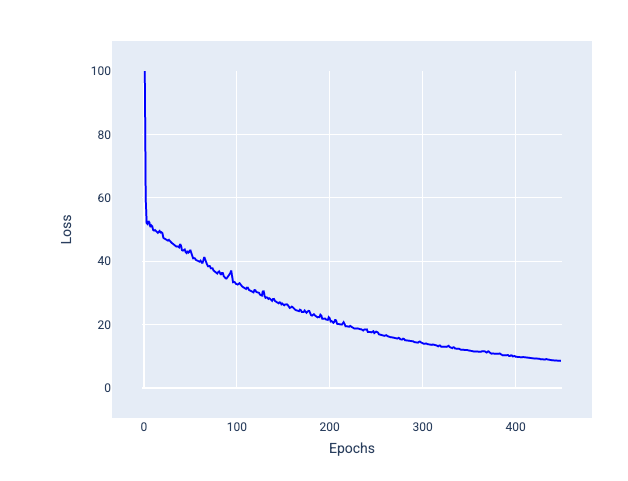
Figura 25. Modelo entrenado con SGD de minilote.
Cuando entrenas un modelo, es posible que pienses que el ruido es una característica no deseada que se debe eliminar. Sin embargo, una cierta cantidad de ruido puede ser algo bueno. En módulos posteriores, aprenderás cómo el ruido puede ayudar a un modelo a generalizar mejor y a encontrar los pesos y el sesgo óptimos en una red neuronal.
Ciclos de entrenamiento
Durante el entrenamiento, un ciclo de entrenamiento significa que el modelo procesó cada ejemplo del conjunto de entrenamiento una vez. Por ejemplo, dado un conjunto de entrenamiento con 1,000 ejemplos y un tamaño de lote pequeño de 100 ejemplos, el modelo tardará 10 iteraciones en completar una época.
Por lo general, el entrenamiento requiere muchas épocas. Es decir, el sistema debe procesar cada ejemplo del conjunto de entrenamiento varias veces.
La cantidad de épocas es un hiperparámetro que estableces antes de que comience el entrenamiento del modelo. En muchos casos, deberás experimentar con la cantidad de épocas que necesita el modelo para converger. En general, más épocas producen un mejor modelo, pero también requieren más tiempo de entrenamiento.
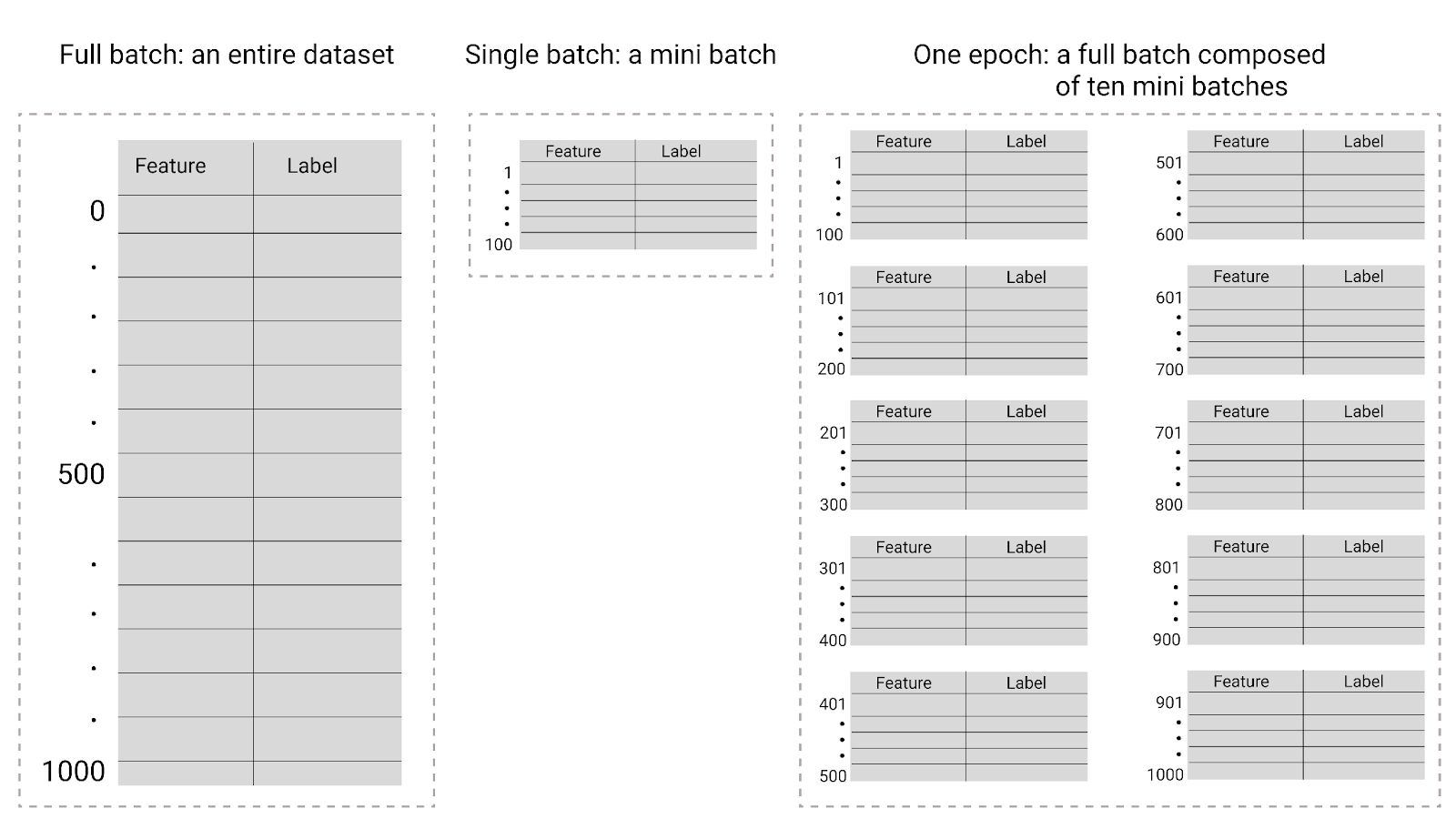
Figura 26. Comparación entre el lote completo y el minilote
En la siguiente tabla, se describe cómo el tamaño del lote y las épocas se relacionan con la cantidad de veces que un modelo actualiza sus parámetros.
| Tipo de lote | Cuándo se producen las actualizaciones de los pesos y el sesgo |
|---|---|
| Lote completo | Después de que el modelo observa todos los ejemplos del conjunto de datos Por ejemplo, si un conjunto de datos contiene 1,000 ejemplos y el modelo se entrena durante 20 épocas, el modelo actualiza los pesos y el sesgo 20 veces, una vez por época. |
| Descenso de gradientes estocástico | Después de que el modelo analiza un solo ejemplo del conjunto de datos Por ejemplo, si un conjunto de datos contiene 1,000 ejemplos y se entrena durante 20 épocas, el modelo actualiza los pesos y la desviación 20,000 veces. |
| Descenso de gradientes estocástico por minilotes | Después de que el modelo analiza los ejemplos de cada lote Por ejemplo, si un conjunto de datos contiene 1,000 ejemplos, el tamaño del lote es 100 y el modelo se entrena durante 20 épocas, el modelo actualiza los pesos y el sesgo 200 veces. |