Hiperparametry to zmienne, które kontrolują różne aspekty trenowania. 3 często używane hiperparametry to:
Z kolei parametry to zmienne, takie jak wagi i odchylenie, które są częścią samego modelu. Inaczej mówiąc, hiperparametry to wartości, które kontrolujesz, a parametry to wartości, które model oblicza podczas trenowania.
Tempo uczenia się
Szybkość uczenia się to ustawiana przez Ciebie liczba zmiennoprzecinkowa, która wpływa na szybkość zbieżności modelu. Jeśli tempo uczenia się jest zbyt niskie, konwergencja modelu może zająć dużo czasu. Jeśli jednak tempo uczenia się jest zbyt wysokie, model nigdy nie osiągnie konwergencji, ale będzie się poruszać w zakresie wag i odchyleń, które minimalizują utratę. Chodzi o wybranie tempa uczenia się, które nie jest ani zbyt wysokie, ani zbyt niskie, aby model szybko osiągnął konwergencję.
Tempo uczenia się określa wielkość zmian, które należy wprowadzić w wagach i odchyleniu na każdym etapie procesu spadku gradientu. Model mnoży gradient przez tempo uczenia się, aby określić parametry modelu (wartości wagi i odchylenia) na potrzeby następnej iteracji. W trzecim kroku metody gradientu prostego „niewielka ilość”, o którą należy się przesunąć w kierunku ujemnego nachylenia, odnosi się do współczynnika uczenia.
Różnica między parametrami starego i nowego modelu jest proporcjonalna do nachylenia funkcji straty. Jeśli na przykład nachylenie jest duże, model wykonuje duży krok. Jeśli jest mała, wykonuje mały krok. Jeśli na przykład wielkość gradientu wynosi 2,5, a szybkość uczenia się to 0,01, model zmieni parametr o 0,025.
Optymalne tempo uczenia się pomaga modelowi zbiegać się w rozsądnej liczbie iteracji. Na rysunku 20 krzywa funkcji straty pokazuje, że model znacznie poprawia się w ciągu pierwszych 20 iteracji, a potem zaczyna zbiegać się do określonej wartości:
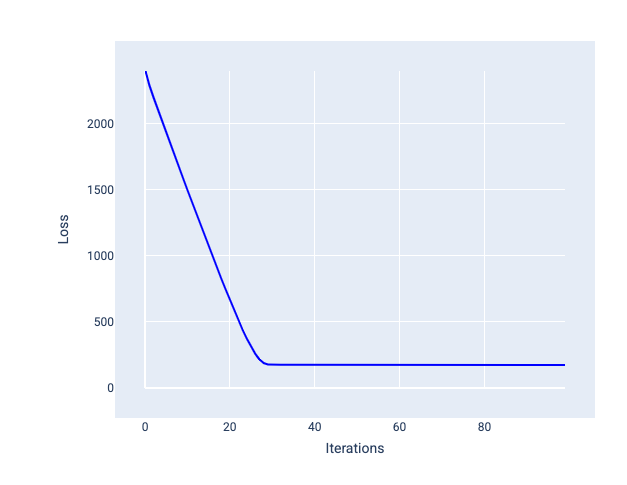
Rysunek 20. Wykres funkcji straty przedstawiający model wytrenowany z użyciem tempa uczenia się, które szybko zbiega się do zera.
Z kolei zbyt mała szybkość uczenia się może wymagać zbyt wielu iteracji, aby osiągnąć zbieżność. Na rysunku 21 krzywa strat pokazuje, że po każdej iteracji model wprowadza tylko niewielkie ulepszenia:
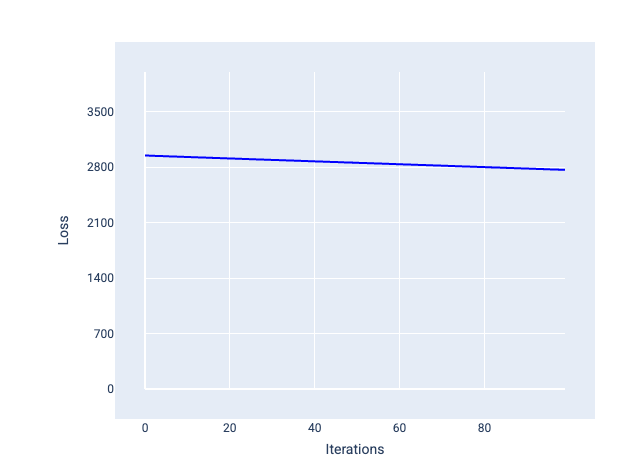
Rysunek 21. Wykres funkcji straty przedstawiający model wytrenowany z małą szybkością uczenia.
Zbyt duże tempo uczenia się nigdy nie zbiega się do wartości optymalnej, ponieważ każda iteracja powoduje wahania lub ciągły wzrost wartości funkcji straty. Na rysunku 22 krzywa utraty pokazuje, że po każdej iteracji utrata modelu najpierw maleje, a potem rośnie. Na rysunku 23 utrata rośnie w późniejszych iteracjach:
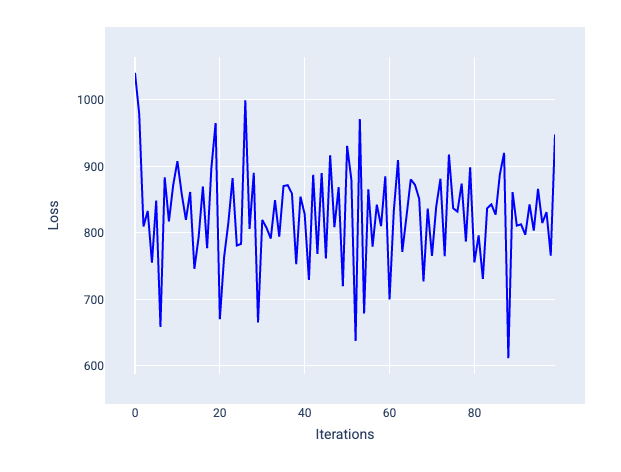
Rysunek 22. Wykres strat przedstawiający model wytrenowany z zbyt dużym tempem uczenia się, na którym krzywa strat gwałtownie się waha, rosnąc i malejąc wraz ze wzrostem liczby iteracji.
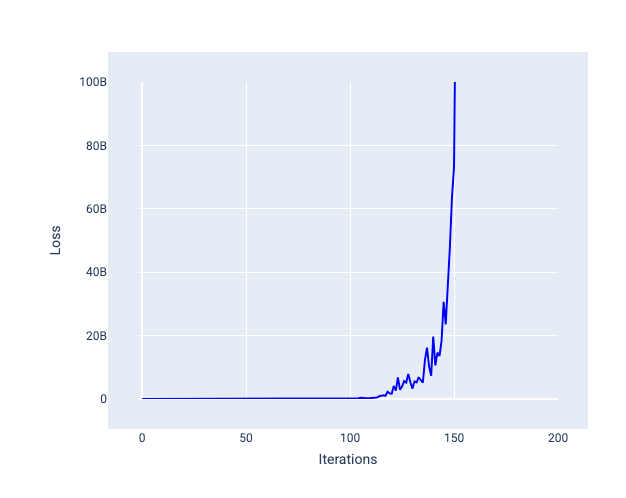
Rysunek 23. Wykres utraty pokazujący model wytrenowany z zbyt dużym tempem uczenia się, w którym krzywa utraty gwałtownie rośnie w późniejszych iteracjach.
Ćwiczenie: sprawdź swoją wiedzę
Wielkość wsadu
Rozmiar partii to hiperparametr, który odnosi się do liczby przykładów, które model przetwarza przed zaktualizowaniem wag i odchylenia. Może Ci się wydawać, że przed zaktualizowaniem wag i wartości progowej model powinien obliczyć funkcję straty dla każdego przykładu w zbiorze danych. Jeśli jednak zbiór danych zawiera setki tysięcy lub nawet miliony przykładów, używanie pełnej partii nie jest praktyczne.
Dwie popularne techniki uzyskiwania odpowiedniego gradientu średniej bez konieczności sprawdzania każdego przykładu w zbiorze danych przed zaktualizowaniem wag i wartości progowej to stochastyczna metoda spadku gradientowego i stochastyczna metoda spadku gradientowego z mini-partiami:
Stochastyczny spadek wzdłuż gradientu (SGD): w każdej iteracji stochastyczny spadek wzdłuż gradientu wykorzystuje tylko 1 przykład (wielkość wsadu równą 1). Przy wystarczającej liczbie iteracji SGD działa, ale jest bardzo niestabilny. „Szum” to zmiany podczas trenowania, które powodują wzrost straty zamiast jej spadku w trakcie iteracji. Określenie „stochastyczny” oznacza, że jeden przykład w każdej partii jest wybierany losowo.
Na poniższym obrazie widać, jak funkcja straty nieznacznie się zmienia, gdy model aktualizuje wagi i wartości progowe za pomocą SGD, co może powodować szum na wykresie funkcji straty:
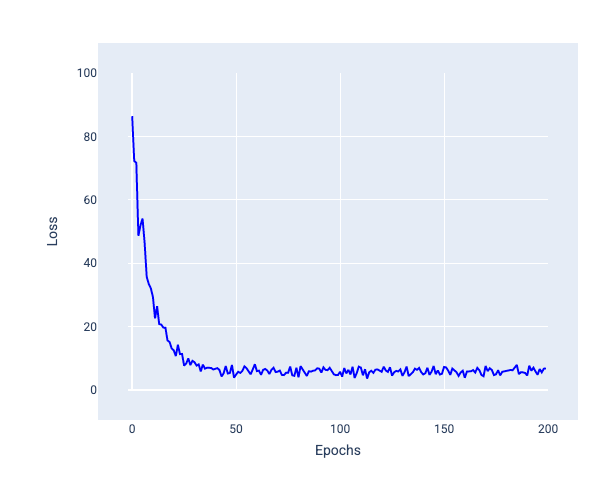
Rysunek 24. Model wytrenowany za pomocą metody stochastycznego spadku wzdłuż gradientu (SGD) wykazujący szum na krzywej funkcji straty.
Pamiętaj, że użycie stochastycznego spadku gradientu może powodować szum na całej krzywej funkcji straty, a nie tylko w pobliżu zbieżności.
Stochastyczny spadek wzdłuż gradientu w przypadku małych partii: stochastyczny spadek wzdłuż gradientu w przypadku małych partii to kompromis między pełną partią a SGD. W przypadku $N $ punktów danych rozmiar partii może być dowolną liczbą większą od 1 i mniejszą od $ N $. Model losowo wybiera przykłady uwzględniane w każdej partii, oblicza średnią ich gradientów, a następnie aktualizuje wagi i odchylenie raz na iterację.
Określenie liczby przykładów w każdej partii zależy od zbioru danych i dostępnych zasobów obliczeniowych. Ogólnie rzecz biorąc, małe rozmiary wsadu działają jak SGD, a większe rozmiary wsadu działają jak pełne opadanie gradientu wsadu.
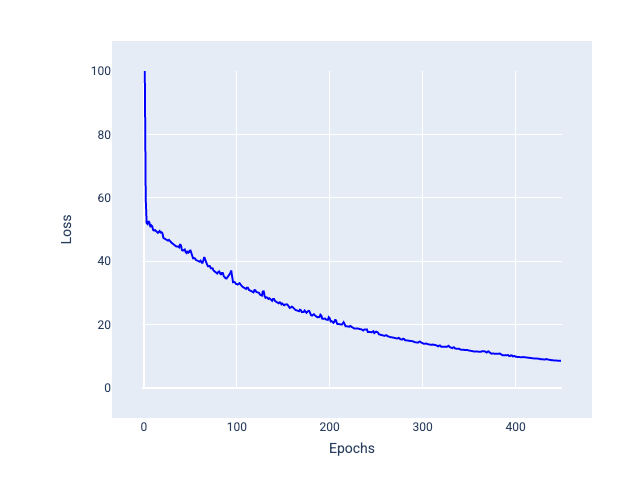
Rysunek 25. Model wytrenowany za pomocą algorytmu SGD z mini-partiami.
Podczas trenowania modelu możesz uznać szum za niepożądaną cechę, którą należy wyeliminować. Jednak pewna ilość szumu może być korzystna. W dalszych modułach dowiesz się, jak szum może pomóc modelowi w lepszym uogólnianiu i znajdowaniu optymalnych wag i odchyleń w sieci neuronowej.
Epoki
Podczas trenowania epoka oznacza, że model przetworzył każdy przykład w zbiorze treningowym raz. Na przykład w przypadku zbioru treningowego zawierającego 1000 przykładów i rozmiaru mini-wsadu wynoszącego 100 przykładów model potrzebuje 10 iteracji, aby ukończyć jedną epokę.
Trenowanie zwykle wymaga wielu epok. Oznacza to, że system musi wielokrotnie przetwarzać każdy przykład w zbiorze treningowym.
Liczba epok to hiperparametr, który ustawiasz, zanim model rozpocznie trenowanie. W wielu przypadkach musisz eksperymentalnie sprawdzić, ile epok jest potrzebnych, aby model osiągnął zbieżność. Ogólnie rzecz biorąc, większa liczba epok daje lepszy model, ale trenowanie zajmuje też więcej czasu.
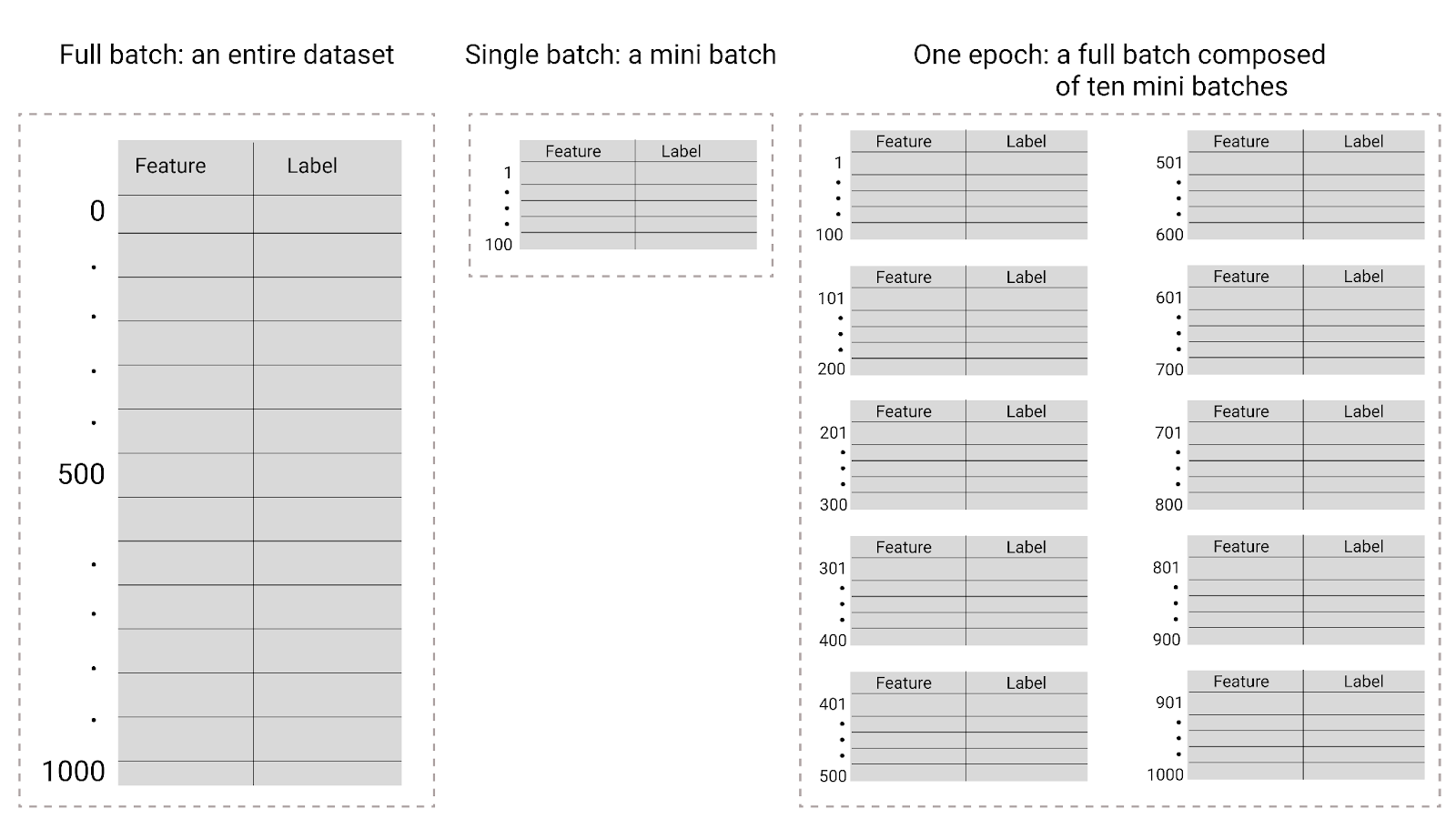
Rysunek 26. Pełna partia a mini partia.
W tabeli poniżej znajdziesz informacje o tym, jak rozmiar partii i liczba epok wpływają na liczbę aktualizacji parametrów modelu.
| Typ wsadu | Gdy nastąpi aktualizacja wag i odchyleń |
|---|---|
| Pełny wsad | Po tym, jak model przeanalizuje wszystkie przykłady w zbiorze danych. Jeśli na przykład zbiór danych zawiera 1000 przykładów, a model trenuje przez 20 epok, wagi i wartości progowe są aktualizowane 20 razy, po jednym razie na epokę. |
| Stochastyczny spadek wzdłuż gradientu | Po tym, jak model przeanalizuje pojedynczy przykład ze zbioru danych. Jeśli na przykład zbiór danych zawiera 1000 przykładów, a model jest trenowany przez 20 epok, wagi i wartości progowe są aktualizowane 20 000 razy. |
| Stochastyczny spadek wzdłuż gradientu w przypadku małych partii | Po tym, jak model przeanalizuje przykłady w każdej partii. Jeśli na przykład zbiór danych zawiera 1000 przykładów, rozmiar partii wynosi 100, a model trenuje przez 20 epok, model aktualizuje wagi i odchylenie 200 razy. |