Hiperparâmetros são variáveis que controlam diferentes aspectos do treinamento. Três hiperparâmetros comuns são:
Já os parâmetros são as variáveis, como os pesos e o viés, que fazem parte do modelo. Em outras palavras, os hiperparâmetros são valores que você controla, e os parâmetros são valores que o modelo calcula durante o treinamento.
Taxa de aprendizado
A taxa de aprendizado é um número de ponto flutuante definido por você que influencia a velocidade de convergência do modelo. Se a taxa de aprendizado for muito baixa, o modelo pode levar muito tempo para convergir. No entanto, se a taxa de aprendizado for muito alta, o modelo nunca vai convergir, mas vai variar em torno dos pesos e do viés que minimizam a perda. O objetivo é escolher uma taxa de aprendizado que não seja muito alta nem muito baixa para que o modelo convirja rapidamente.
A taxa de aprendizado determina a magnitude das mudanças a serem feitas nos pesos e no viés durante cada etapa do processo de descida do gradiente. O modelo multiplica o gradiente pela taxa de aprendizado para determinar os parâmetros do modelo (valores de peso e bias) para a próxima iteração. Na terceira etapa do descida do gradiente, a "pequena quantidade" a ser movida na direção da inclinação negativa se refere à taxa de aprendizado.
A diferença entre os parâmetros do modelo antigo e do novo é proporcional à inclinação da função de perda. Por exemplo, se a inclinação for grande, o modelo vai dar um passo grande. Se for pequeno, ele dá um passo pequeno. Por exemplo, se a magnitude do gradiente for 2,5 e a taxa de aprendizado for 0,01, o modelo vai mudar o parâmetro em 0,025.
A taxa de aprendizado ideal ajuda o modelo a convergir em um número razoável de iterações. Na Figura 20, a curva de perda mostra que o modelo melhora significativamente durante as primeiras 20 iterações antes de começar a convergir:
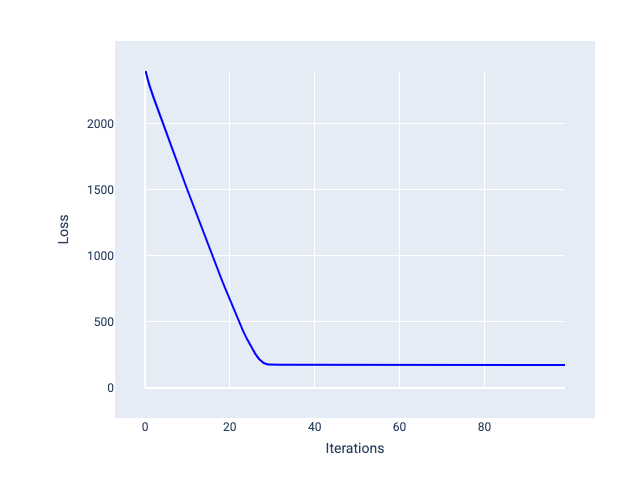
Figura 20. Gráfico de perda mostrando um modelo treinado com uma taxa de aprendizado que converge rapidamente.
Por outro lado, uma taxa de aprendizado muito pequena pode levar muitas iterações para convergir. Na Figura 21, a curva de perda mostra que o modelo faz apenas pequenas melhorias após cada iteração:
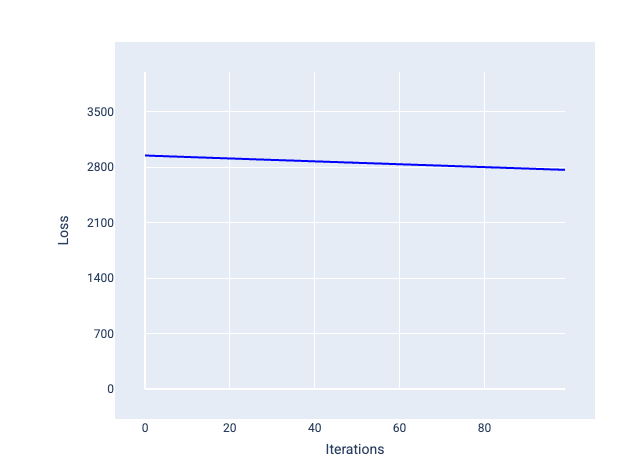
Figura 21. Gráfico de perda mostrando um modelo treinado com uma taxa de aprendizado pequena.
Uma taxa de aprendizado muito alta nunca converge porque cada iteração faz com que a perda varie ou aumente continuamente. Na Figura 22, a curva de perda mostra o modelo diminuindo e aumentando a perda após cada iteração. Na Figura 23, a perda aumenta nas iterações posteriores:
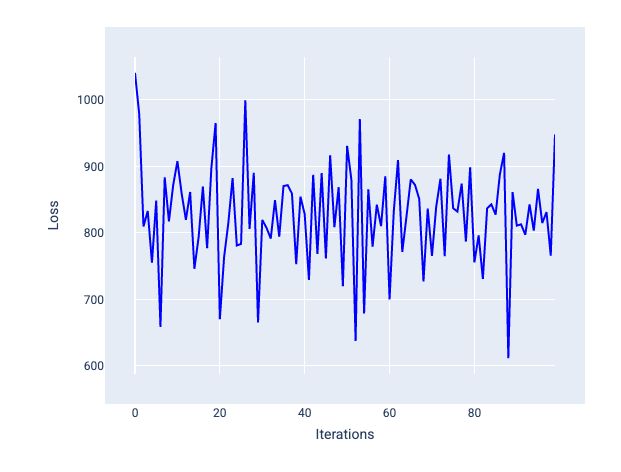
Figura 22. Gráfico de perda mostrando um modelo treinado com uma taxa de aprendizado muito alta, em que a curva de perda oscila muito, subindo e descendo conforme as iterações aumentam.
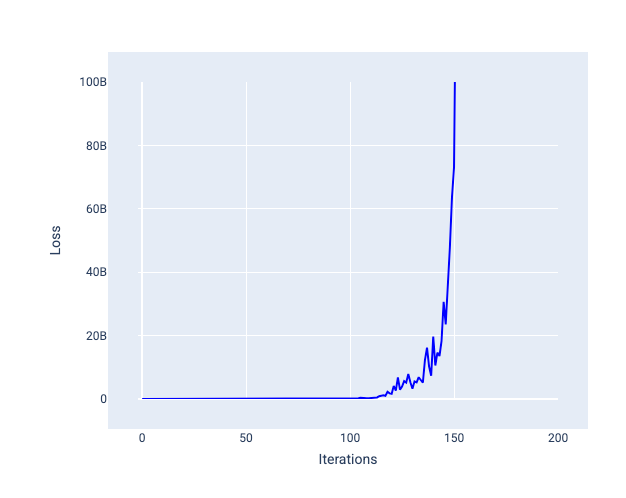
Figura 23. Gráfico de perda mostrando um modelo treinado com uma taxa de aprendizado muito alta, em que a curva de perda aumenta drasticamente nas iterações posteriores.
Exercício: teste de conhecimentos
Tamanho do lote
O tamanho do lote é um hiperparâmetro que se refere ao número de exemplos que o modelo processa antes de atualizar os pesos e o viés. Você pode pensar que o modelo precisa calcular a perda para todos os exemplos no conjunto de dados antes de atualizar os pesos e o bias. No entanto, quando um conjunto de dados contém centenas de milhares ou até milhões de exemplos, usar o lote completo não é prático.
Duas técnicas comuns para obter o gradiente médio sem precisar analisar todos os exemplos no conjunto de dados antes de atualizar os pesos e o bias são descida do gradiente estocástico e descida do gradiente estocástico de minilote:
Gradiente descendente estocástico (GDE): usa apenas um exemplo (tamanho do lote de um) por iteração. Com iterações suficientes, o SGD funciona, mas é muito ruidoso. "Ruído" se refere a variações durante o treinamento que fazem com que a perda aumente em vez de diminuir durante uma iteração. O termo "estocástico" indica que o exemplo que compõe cada lote é escolhido aleatoriamente.
Na imagem a seguir, observe como a perda varia um pouco à medida que o modelo atualiza os pesos e o viés usando o SGD, o que pode gerar ruído no gráfico de perda:
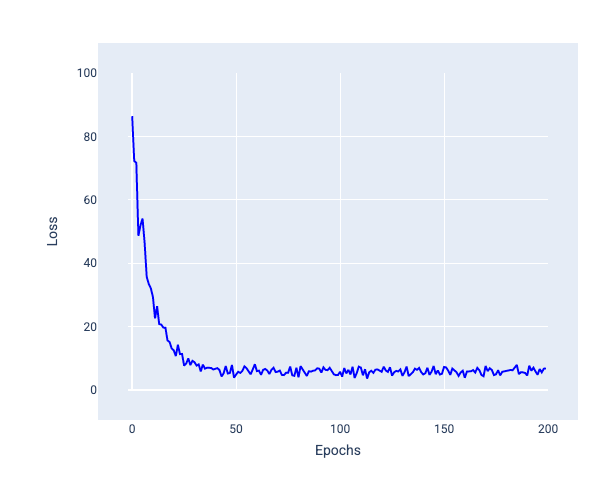
Figura 24. Modelo treinado com gradiente descendente estocástico (GDE) mostrando ruído na curva de perda.
O uso da descida do gradiente estocástico pode gerar ruído em toda a curva de perda, não apenas perto da convergência.
Gradiente descendente estocástico com minilotes (GDE com minilotes): o GDE com minilotes é um meio-termo entre o GDE com lote completo e o GDE. Para $ N $ pontos de dados, o tamanho do lote pode ser qualquer número maior que 1 e menor que $ N $. O modelo escolhe aleatoriamente os exemplos incluídos em cada lote, calcula a média dos gradientes e atualiza os pesos e o bias uma vez por iteração.
Determinar o número de exemplos para cada lote depende do conjunto de dados e dos recursos de computação disponíveis. Em geral, tamanhos de lote pequenos se comportam como SGD, e tamanhos de lote maiores se comportam como descida de gradiente de lote completo.
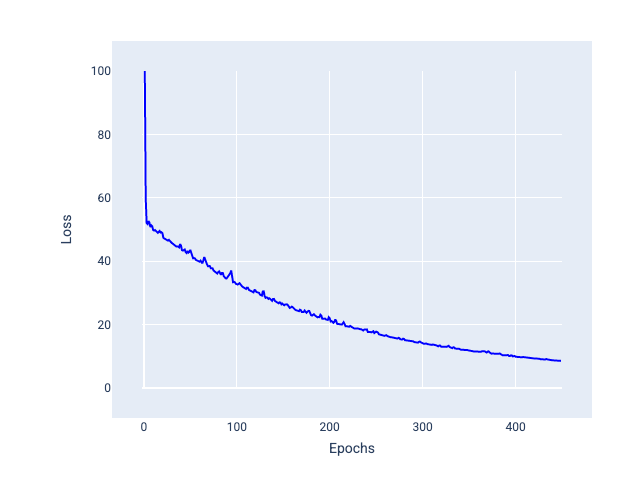
Figura 25. Modelo treinado com GDE de minilotes.
Ao treinar um modelo, você pode pensar que o ruído é uma característica indesejável que deve ser eliminada. No entanto, uma certa quantidade de ruído pode ser boa. Em módulos posteriores, você vai aprender como o ruído pode ajudar um modelo a generalizar melhor e encontrar os pesos e o viés ideais em uma rede neural.
Períodos
Durante o treinamento, uma época significa que o modelo processou uma vez cada exemplo no conjunto de treinamento. Por exemplo, considerando um conjunto de treinamento com 1.000 exemplos e um tamanho de mini-lote de 100 exemplos, o modelo vai levar 10 iterações para concluir uma época.
O treinamento geralmente requer muitas épocas. Ou seja, o sistema precisa processar cada exemplo no conjunto de treinamento várias vezes.
O número de épocas é um hiperparâmetro definido antes do início do treinamento do modelo. Em muitos casos, é necessário testar quantas épocas são necessárias para que o modelo convirja. Em geral, mais épocas produzem um modelo melhor, mas também levam mais tempo para treinar.
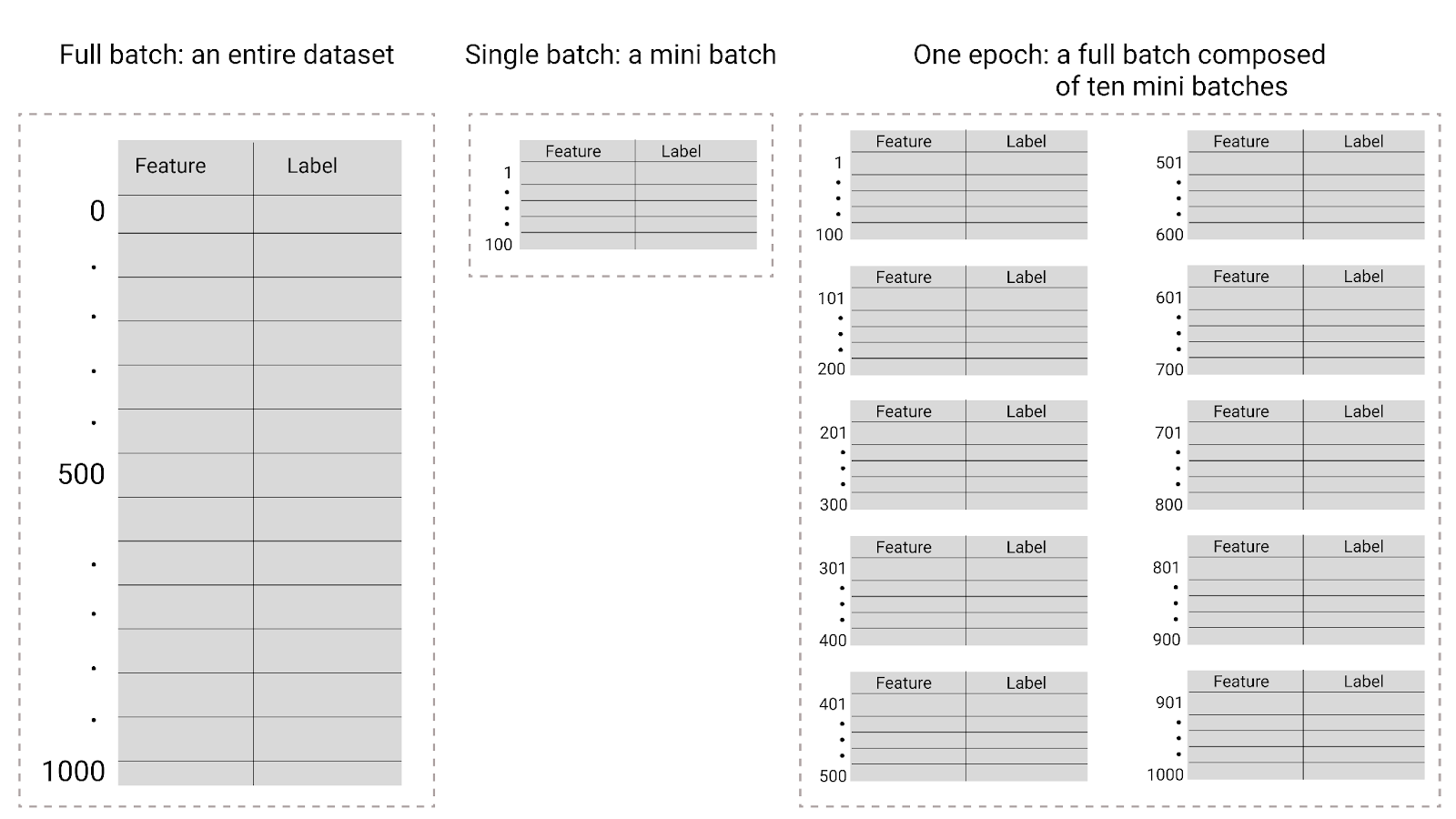
Figura 26. Lote completo x minilote.
A tabela a seguir descreve como o tamanho do lote e as épocas se relacionam com o número de vezes que um modelo atualiza os parâmetros.
| Tipo de lote | Quando as atualizações de pesos e vieses ocorrem |
|---|---|
| Lote completo | Depois que o modelo analisa todos os exemplos no conjunto de dados. Por exemplo, se um conjunto de dados tiver 1.000 exemplos e o modelo for treinado por 20 épocas, ele vai atualizar os pesos e o bias 20 vezes, uma vez por época. |
| Gradiente descendente estocástico | Depois que o modelo analisa um único exemplo do conjunto de dados. Por exemplo, se um conjunto de dados tiver 1.000 exemplos e for treinado por 20 épocas, o modelo vai atualizar os pesos e o bias 20.000 vezes. |
| Gradiente descendente estocástico em minilote | Depois que o modelo analisa os exemplos em cada lote. Por exemplo, se um conjunto de dados tiver 1.000 exemplos, o tamanho do lote for 100 e o modelo for treinado por 20 épocas, ele vai atualizar os pesos e o bias 200 vezes. |