超参数是控制训练不同方面的变量。以下是三种常见的超参数:
相比之下,形参是模型本身的一部分,例如权重和偏差。换句话说,超参数是您控制的值;参数是模型在训练期间计算的值。
学习速率
学习速率是一个您设置的浮点数,用于影响模型收敛的速度。如果学习率过低,模型可能需要很长时间才能收敛。不过,如果学习速率过高,模型将永远无法收敛,而是在可最大限度减少损失的权重和偏差附近跳动。目标是选择一个既不太高也不太低的学习速率,以便模型快速收敛。
学习速率决定了在梯度下降过程的每一步中,对权重和偏差所做的更改幅度。模型将梯度乘以学习速率,以确定下一次迭代的模型参数(权重和偏差值)。在梯度下降的第三步中,沿负斜率方向移动的“少量”是指学习速率。
旧模型参数与新模型参数之间的差异与损失函数的斜率成正比。例如,如果斜率较大,模型会采取较大的步长。如果较小,则采取较小的步长。例如,如果梯度的大小为 2.5,学习率为 0.01,则模型会将形参更改 0.025。
理想的学习率有助于模型在合理的迭代次数内收敛。在图 20 中,损失曲线显示模型在前 20 次迭代中显著改进,然后开始收敛:
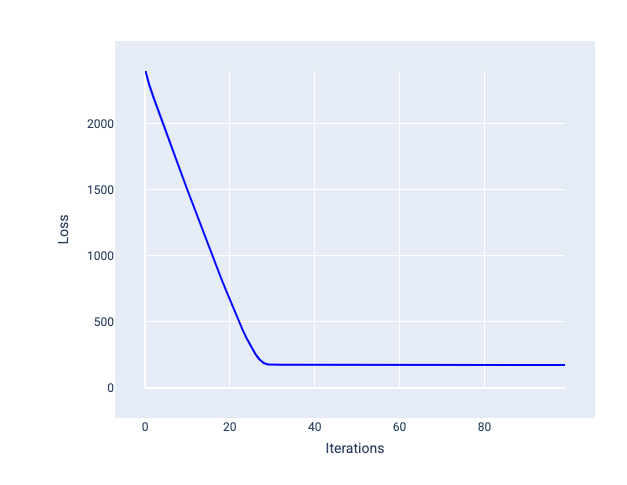
图 20. 损失图,显示了以可快速收敛的学习速率训练的模型。
相比之下,如果学习速率过小,则可能需要过多的迭代次数才能实现收敛。在图 21 中,损失曲线显示模型在每次迭代后仅略有改进:
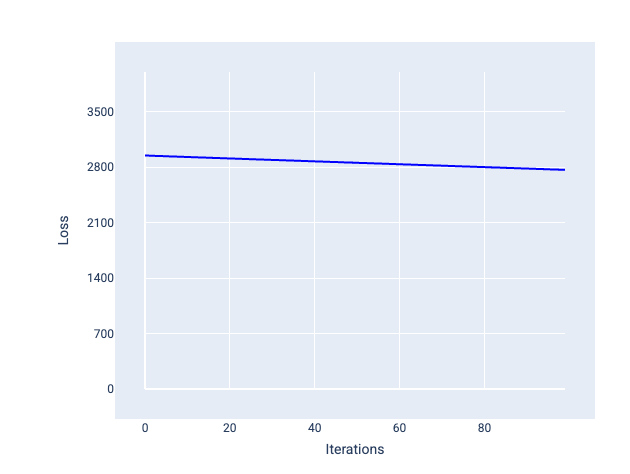
图 21. 损失图,显示了以较小学习速率训练的模型。
过大的学习速率永远不会收敛,因为每次迭代都会导致损失在较大范围内波动或持续增加。在图 22 中,损失曲线显示模型在每次迭代后损失先减少后增加;在图 23 中,损失在后续迭代中增加:
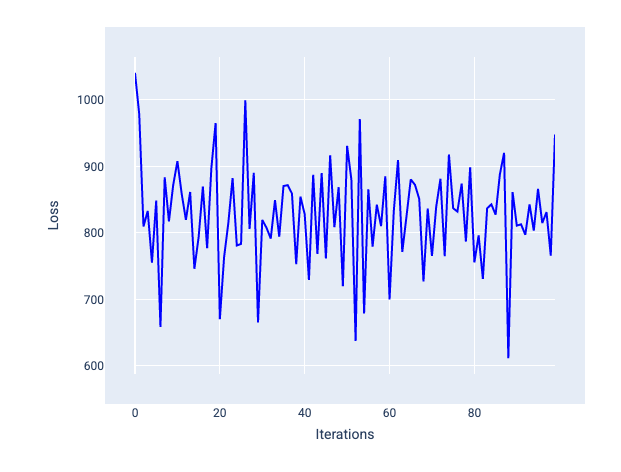
图 22. 损失图,显示了以过大的学习速率训练的模型,其中损失曲线随着迭代次数的增加而剧烈波动,时而上升时而下降。
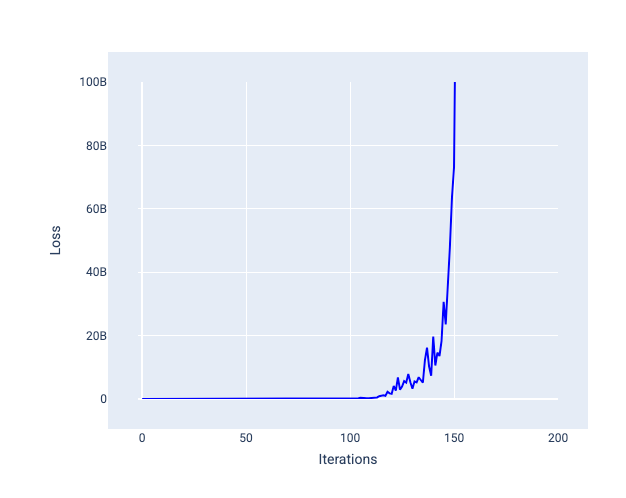
图 23. 损失图,显示了以过大的学习速率训练的模型,其中损失曲线在后来的迭代中急剧增加。
练习:检查您的理解情况
批次大小
批次大小是一种超参数,指的是模型在更新权重和偏差之前处理的示例数量。您可能会认为,模型应先计算数据集中每个样本的损失,然后再更新权重和偏差。不过,如果数据集包含数十万甚至数百万个示例,则使用完整批次并不实际。
以下两种常见技术可在不查看数据集中的每个示例的情况下,获得正确的平均梯度,然后更新权重和偏差:随机梯度下降和小批量随机梯度下降。
随机梯度下降法 (SGD):随机梯度下降法在每次迭代中仅使用一个示例(批次大小为 1)。在迭代次数足够多的情况下,SGD 可以正常运行,但噪声非常大。“噪声”是指训练期间导致损失在迭代过程中增加而非减少的变化。“随机”一词表示每个批次中的一个示例是随机选择的。
请注意,在下图中,当模型使用 SGD 更新权重和偏差时,损失会略有波动,这可能会导致损失图出现噪声:
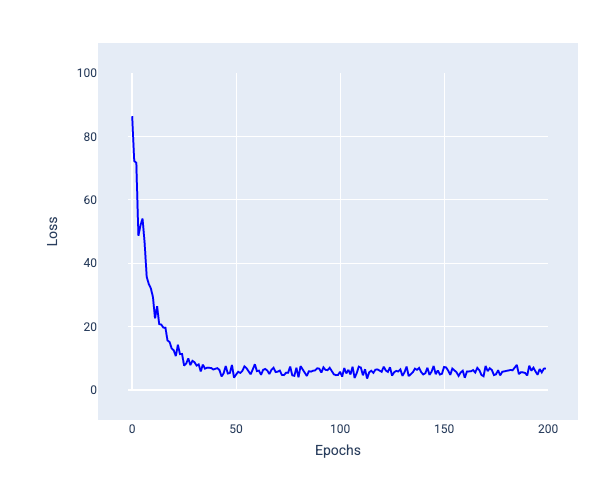
图 24. 使用随机梯度下降法 (SGD) 训练的模型,显示损失曲线中的噪声。
请注意,使用随机梯度下降可能会在整个损失曲线中产生噪声,而不仅仅是在接近收敛时。
小批次随机梯度下降法(小批次 SGD):小批次随机梯度下降法是全批次和 SGD 之间的折衷方案。对于 $ N $ 个数据点,批次大小可以是大于 1 且小于 $ N $ 的任意数字。模型会随机选择每个批次中包含的示例,对它们的梯度求平均值,然后在每次迭代中更新一次权重和偏差。
确定每个批次的样本数量取决于数据集和可用的计算资源。一般来说,小批量大小的行为类似于 SGD,而大批量大小的行为类似于全批量梯度下降。
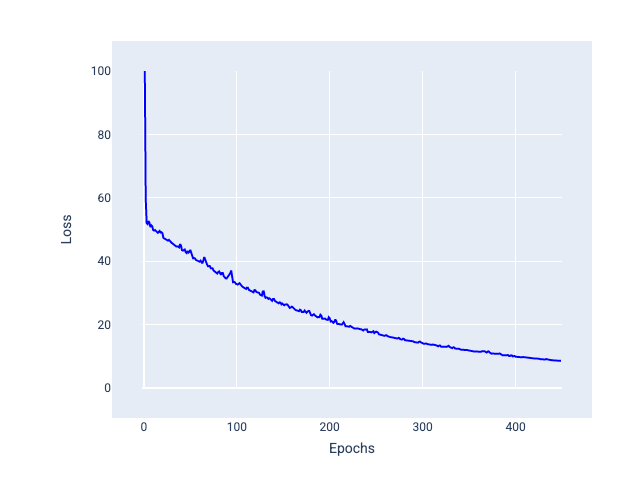
图 25. 使用小批次随机梯度下降法训练的模型。
在训练模型时,您可能会认为噪声是一种应消除的不良特征。不过,一定程度的噪音可能是一件好事。在后续模块中,您将了解噪声如何帮助模型更好地泛化,以及如何在神经网络中找到最佳权重和偏差。
周期数
在训练期间,一个周期是指模型已处理训练集中的每个示例一次。例如,如果训练集包含 1,000 个示例,而小批次大小为 100 个示例,则模型需要 10 次迭代才能完成一个周期。
训练通常需要多个周期。也就是说,系统需要多次处理训练集中的每个示例。
周期数是一种超参数,您需要在模型开始训练之前设置该参数。在许多情况下,您需要通过实验来确定模型收敛所需的周期数。一般来说,训练周期数越多,模型效果越好,但训练时间也越长。
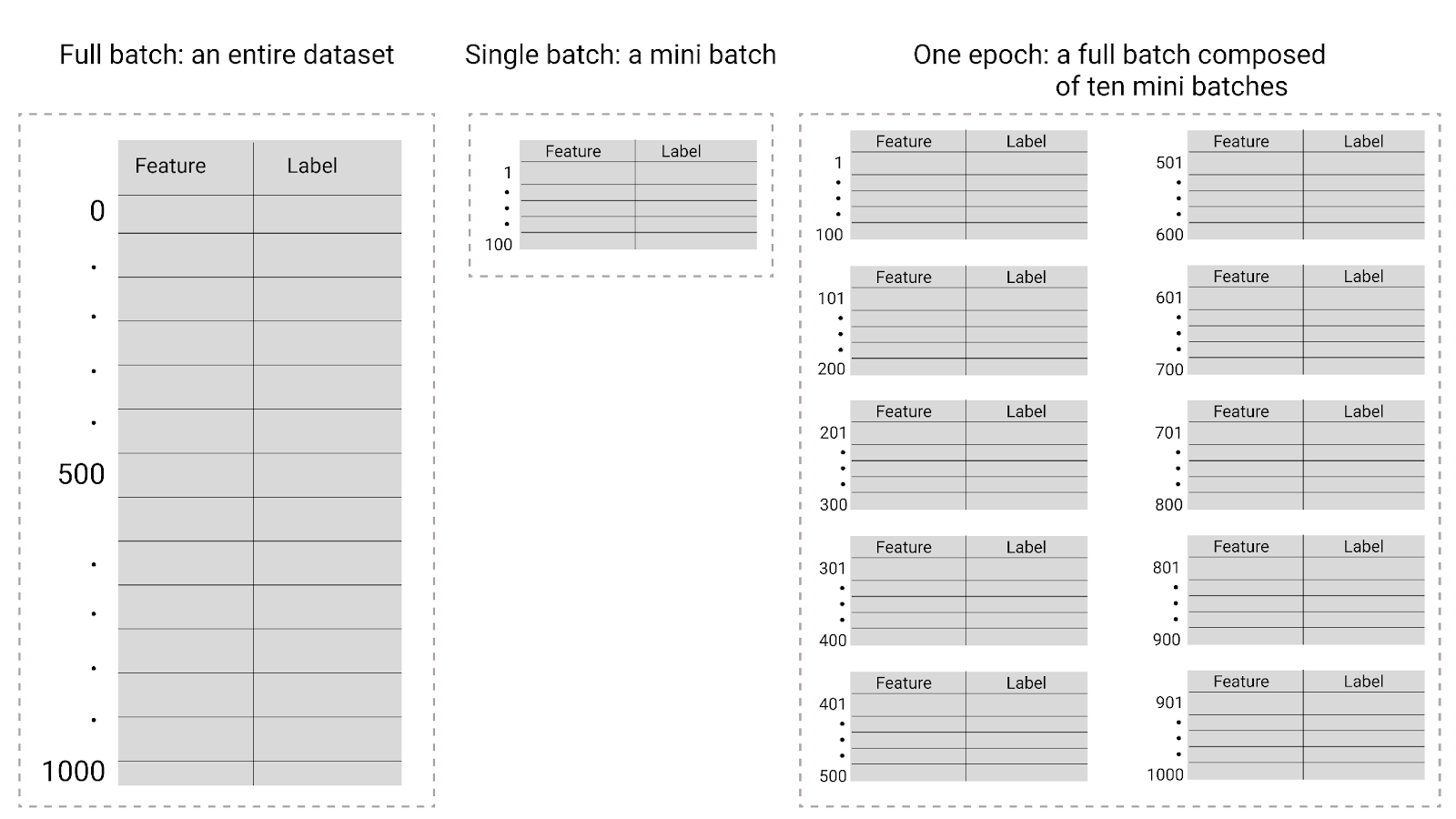
图 26. 完整批次与小批次。
下表介绍了批次大小和周期与模型更新其参数的次数之间的关系。
| 批次类型 | 权重和偏差更新何时发生 |
|---|---|
| 完整批次 | 模型查看完数据集中的所有示例后。例如,如果某个数据集包含 1,000 个样本,并且模型训练了 20 个周期,则模型会更新权重和偏差 20 次,每个周期更新一次。 |
| 随机梯度下降法 | 模型查看数据集中的单个示例后。 例如,如果某个数据集包含 1,000 个样本,并且训练了 20 个周期,则模型会更新权重和偏差 20,000 次。 |
| 小批次随机梯度下降法 | 模型查看完每个批次中的示例后。例如,如果某个数据集包含 1,000 个样本,批次大小为 100,并且模型训练了 20 个周期,则模型会更新权重和偏差 200 次。 |
