Hyperparameter sind Variablen, mit denen verschiedene Aspekte des Trainings gesteuert werden. Drei gängige Hyperparameter sind:
Im Gegensatz dazu sind Parameter die Variablen, z. B. die Gewichte und der Bias, die Teil des Modells selbst sind. Mit anderen Worten: Hyperparameter sind Werte, die Sie steuern, und Parameter sind Werte, die das Modell während des Trainings berechnet.
Lernrate
Die Lernrate ist eine von Ihnen festgelegte Gleitkommazahl, die beeinflusst, wie schnell das Modell konvergiert. Wenn die Lernrate zu niedrig ist, kann es lange dauern, bis das Modell konvergiert. Wenn die Lernrate jedoch zu hoch ist, konvergiert das Modell nie, sondern schwankt um die Gewichte und den Bias, die den Verlust minimieren. Das Ziel ist, eine Lernrate zu wählen, die weder zu hoch noch zu niedrig ist, damit das Modell schnell konvergiert.
Die Lernrate bestimmt die Größe der Änderungen, die an den Gewichten und dem Bias in jedem Schritt des Gradientenabstiegs vorgenommen werden. Das Modell multipliziert den Gradienten mit der Lernrate, um die Parameter des Modells (Gewichtungs- und Bias-Werte) für die nächste Iteration zu bestimmen. Im dritten Schritt des Gradientenabstiegs bezieht sich der „kleine Betrag“, um den in Richtung des negativen Anstiegs verschoben wird, auf die Lernrate.
Der Unterschied zwischen den alten und den neuen Modellparametern ist proportional zur Steigung der Verlustfunktion. Wenn die Steigung beispielsweise groß ist, macht das Modell einen großen Schritt. Wenn der Unterschied gering ist, wird ein kleiner Schritt ausgeführt. Wenn beispielsweise die Größe des Gradienten 2,5 und die Lernrate 0,01 ist, ändert das Modell den Parameter um 0,025.
Die ideale Lernrate trägt dazu bei, dass das Modell innerhalb einer angemessenen Anzahl von Iterationen konvergiert. In Abbildung 20 ist zu sehen, dass sich das Modell in den ersten 20 Iterationen deutlich verbessert, bevor es konvergiert:
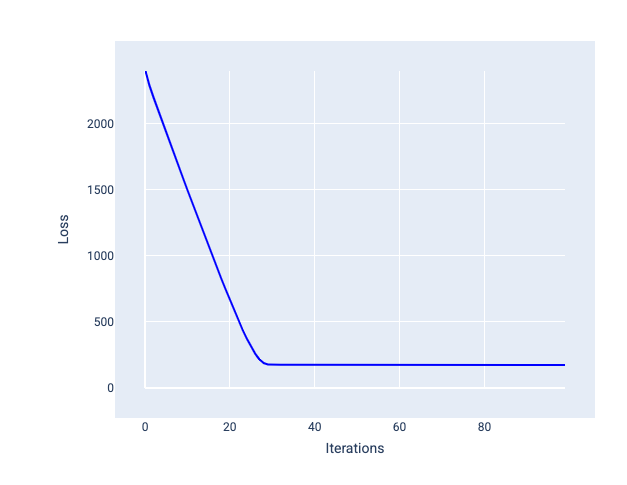
Abbildung 20. Verlustdiagramm für ein Modell, das mit einer Lernrate trainiert wurde, die schnell konvergiert.
Eine zu kleine Lernrate kann dagegen zu viele Iterationen erfordern, bis die Konvergenz erreicht ist. In Abbildung 21 ist zu sehen, dass das Modell nach jeder Iteration nur geringfügige Verbesserungen erzielt:
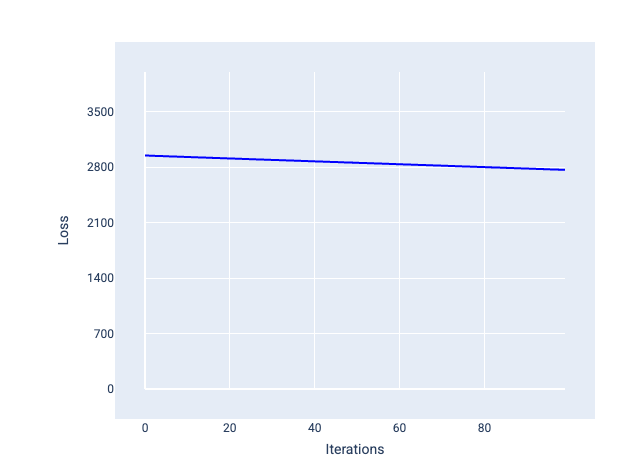
Abbildung 21. Verlustdiagramm für ein Modell, das mit einer niedrigen Lernrate trainiert wurde.
Bei einer zu großen Lernrate wird nie eine Konvergenz erreicht, da der Verlust bei jeder Iteration entweder schwankt oder kontinuierlich zunimmt. In Abbildung 22 ist zu sehen, dass der Verlust des Modells nach jeder Iteration zuerst abnimmt und dann wieder zunimmt. In Abbildung 23 nimmt der Verlust in späteren Iterationen zu:
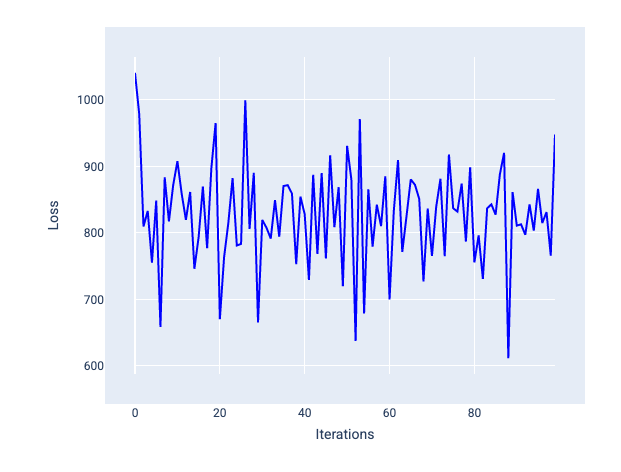
Abbildung 22. Verlustdiagramm für ein Modell, das mit einer zu hohen Lernrate trainiert wurde. Die Verlustkurve schwankt stark und steigt und fällt mit zunehmenden Iterationen.
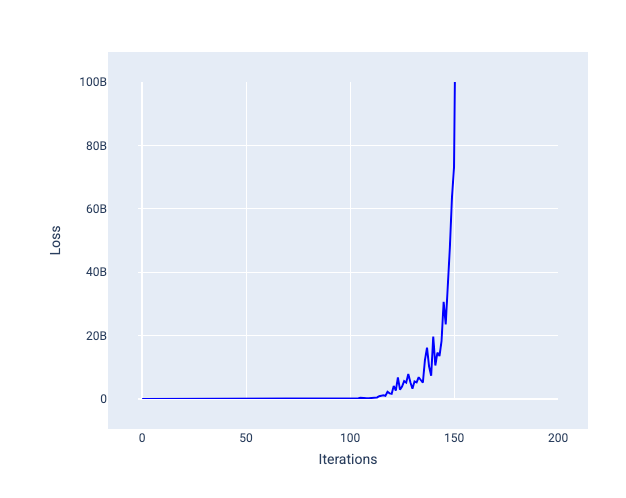
Abbildung 23. Verlustdiagramm für ein Modell, das mit einer zu hohen Lernrate trainiert wurde. Die Verlustkurve steigt in späteren Iterationen drastisch an.
Übung: Wissen testen
Batchgröße
Die Batchgröße ist ein Hyperparameter, der sich auf die Anzahl der Beispiele bezieht, die das Modell verarbeitet, bevor es seine Gewichte und seinen Bias aktualisiert. Vielleicht denken Sie, dass das Modell den Verlust für jedes Beispiel im Dataset berechnen sollte, bevor die Gewichte und der Bias aktualisiert werden. Wenn ein Dataset jedoch Hunderttausende oder sogar Millionen von Beispielen enthält, ist die Verwendung des vollständigen Batches nicht praktikabel.
Zwei gängige Methoden, um den richtigen Gradienten im Durchschnitt zu erhalten, ohne jedes Beispiel im Dataset vor der Aktualisierung der Gewichte und des Bias zu berücksichtigen, sind stochastischer Gradientenabstieg und stochastischer Gradientenabstieg mit Mini-Batch:
Stochastischer Gradientenabstieg (SGD): Beim stochastischen Gradientenabstieg wird pro Iteration nur ein einzelnes Beispiel (Batchgröße 1) verwendet. Bei genügend Iterationen funktioniert SGD, ist aber sehr verrauscht. „Rauschen“ bezieht sich auf Schwankungen während des Trainings, die dazu führen, dass der Verlust in einer Iteration steigt statt sinkt. Der Begriff „stochastisch“ bedeutet, dass das eine Beispiel, aus dem jeder Batch besteht, zufällig ausgewählt wird.
Auf dem folgenden Bild sehen Sie, wie der Verlust leicht schwankt, wenn das Modell seine Gewichte und den Bias mit SGD aktualisiert. Dies kann zu Rauschen im Verlustdiagramm führen:
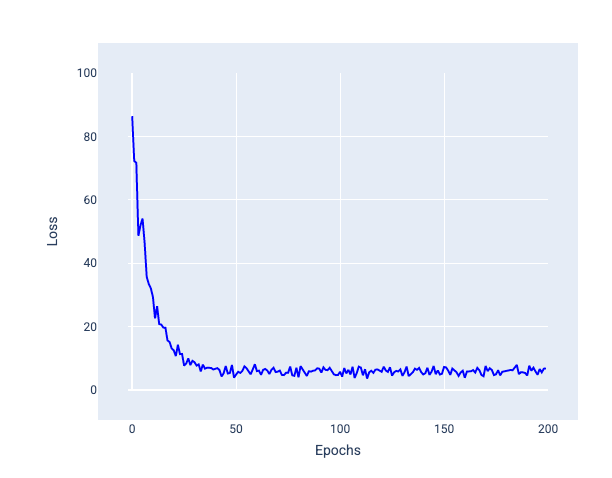
Abbildung 24. Mit stochastischem Gradientenabstieg (SGD) trainiertes Modell mit Rauschen in der Verlustkurve.
Beachten Sie, dass der stochastische Gradientenabstieg nicht nur in der Nähe der Konvergenz, sondern über die gesamte Verlustkurve hinweg Rauschen verursachen kann.
Stochastischer Gradientenabstieg mit Mini-Batch (Mini-Batch SGD): Der stochastische Gradientenabstieg mit Mini-Batch ist ein Kompromiss zwischen Full-Batch und SGD. Bei $N $ Datenpunkten kann die Batchgröße eine beliebige Zahl größer als 1 und kleiner als $ N$ sein. Das Modell wählt die in jedem Batch enthaltenen Beispiele zufällig aus, berechnet den Durchschnitt ihrer Gradienten und aktualisiert dann die Gewichte und den Bias einmal pro Iteration.
Die Anzahl der Beispiele für jeden Batch hängt vom Dataset und den verfügbaren Rechenressourcen ab. Im Allgemeinen verhalten sich kleine Batchgrößen wie SGD und größere Batchgrößen wie der Gradientenabstieg für den gesamten Batch.
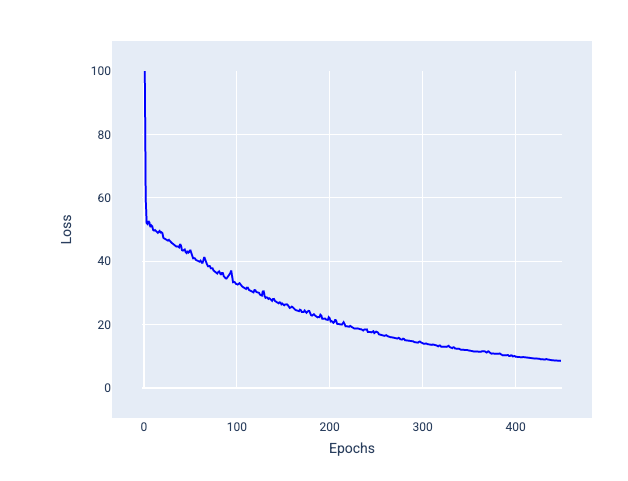
Abbildung 25. Mit Mini-Batch-SGD trainiertes Modell.
Beim Trainieren eines Modells könnte man meinen, dass Rauschen eine unerwünschte Eigenschaft ist, die eliminiert werden sollte. Ein gewisses Maß an Rauschen kann jedoch von Vorteil sein. In späteren Modulen erfahren Sie, wie Rauschen einem Modell helfen kann, besser zu generalisieren und die optimalen Gewichte und den optimalen Bias in einem neuronalen Netzwerk zu finden.
Epochen
Während des Trainings bedeutet eine Epoche, dass das Modell jedes Beispiel im Trainingsset einmal verarbeitet hat. Wenn Sie beispielsweise einen Trainingssatz mit 1.000 Beispielen und eine Mini-Batchgröße von 100 Beispielen haben, benötigt das Modell 10 Iterationen, um eine Epoche abzuschließen.
Für das Training sind in der Regel viele Epochen erforderlich. Das bedeutet, dass das System jedes Beispiel im Trainingsset mehrmals verarbeiten muss.
Die Anzahl der Epochen ist ein Hyperparameter, den Sie festlegen, bevor das Modell mit dem Training beginnt. In vielen Fällen müssen Sie experimentieren, wie viele Epochen erforderlich sind, bis das Modell konvergiert. Im Allgemeinen führt eine höhere Anzahl von Epochen zu einem besseren Modell, das Training dauert aber auch länger.
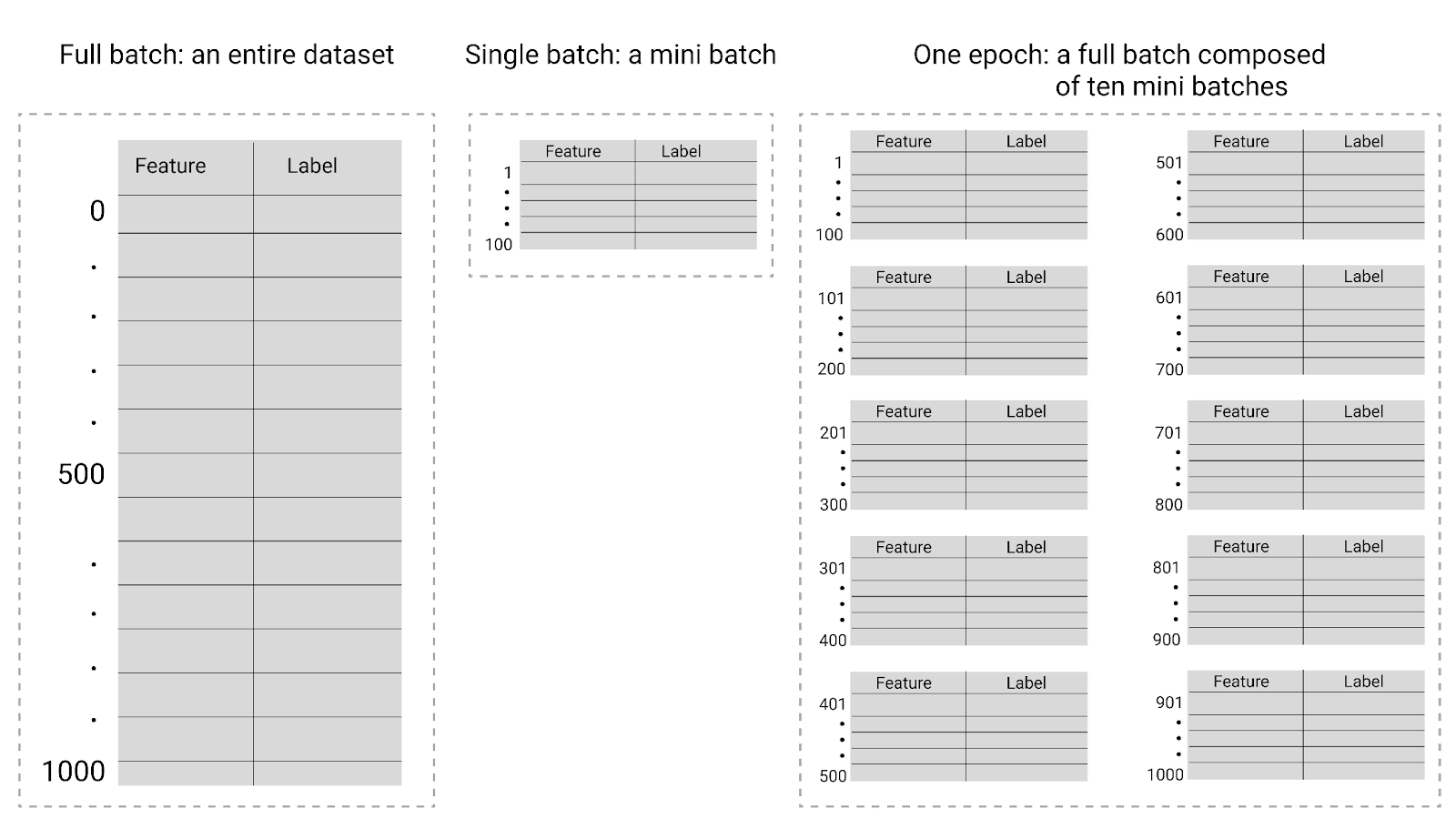
Abbildung 26. Vollständiger Batch im Vergleich zu Mini-Batch.
In der folgenden Tabelle wird beschrieben, wie sich die Batchgröße und die Epochen auf die Anzahl der Aktualisierungen der Parameter eines Modells auswirken.
| Batchtyp | Wann werden Gewichte und Bias aktualisiert? |
|---|---|
| Vollständiger Batch | Nachdem das Modell alle Beispiele im Dataset betrachtet hat. Wenn ein Dataset beispielsweise 1.000 Beispiele enthält und das Modell 20 Epochen lang trainiert wird, werden die Gewichte und der Bias des Modells 20-mal aktualisiert, einmal pro Epoche. |
| Stochastic Gradient Descent | Nachdem das Modell ein einzelnes Beispiel aus dem Dataset betrachtet hat. Wenn ein Dataset beispielsweise 1.000 Beispiele enthält und 20 Epochen lang trainiert wird, werden die Gewichte und der Bias des Modells 20.000 Mal aktualisiert. |
| Mini-Batch Stochastic Gradient Descent | Nachdem das Modell die Beispiele in jedem Batch betrachtet hat. Wenn ein Dataset beispielsweise 1.000 Beispiele enthält, die Batchgröße 100 beträgt und das Modell 20 Epochen lang trainiert wird, werden die Gewichte und der Bias des Modells 200 Mal aktualisiert. |