Гіперпараметри – це змінні, які контролюють різні аспекти навчання. Нижче наведено три найпоширеніші гіперпараметри.
Натомість параметри – це змінні, такі як значення ваги й упередженість, які є частиною самої моделі. Іншими словами, гіперпараметри – це значення, якими ви керуєте, а параметри – значення, які модель обчислює під час навчання.
Швидкість навчання
Швидкість навчання – це число з рухомою комою, яке вказуєте ви і яке впливає на швидкість збіжності моделі. Якщо швидкість навчання занизька, збіжність моделі може зайняти багато часу. Однак якщо вона зависока, модель ніколи не збігається, а натомість коливається навколо значень ваги й упередженості, які мінімізують втрати. Потрібно вибрати швидкість навчання, яка не буде ні зависокою, ні занизькою, щоб модель швидко збігалася.
Швидкість навчання визначає величину змін, які необхідно застосовувати до значень ваги й упередженості на кожному кроці градієнтного спуску. Модель множить градієнт на швидкість навчання, щоб визначити свої параметри (значення ваги й упередженості) для наступної ітерації. На третьому кроці градієнтного спуску "невелика кількість", яку потрібно перемістити в напрямку від’ємного нахилу, стосується швидкості навчання.
Різниця між параметрами старої і нової моделі пропорційна нахилу функції втрат. Якщо нахил значний, модель робить великий крок, а якщо незначний – малий крок. Наприклад, якщо величина градієнта дорівнює 2,5, а швидкість навчання становить 0,01, то модель змінить параметр на 0,025.
Ідеальна швидкість навчання допомагає моделі збігатися в межах прийнятної кількості ітерацій. Крива втрат із рисунка 21 свідчить про значне покращення моделі впродовж перших 20 ітерацій до того, як вона почала збігатися.
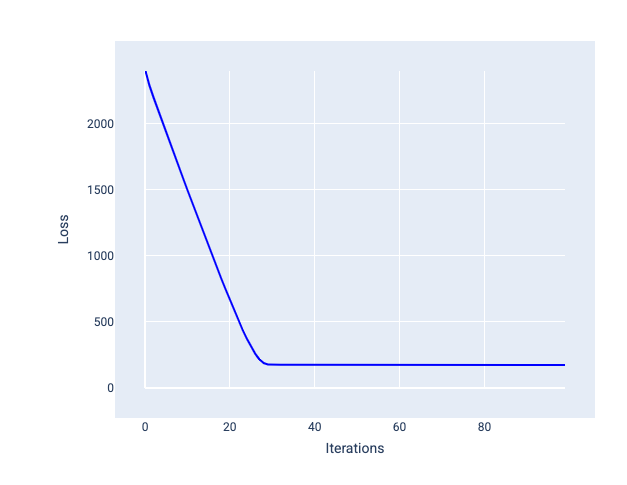
Рисунок 21. Графік втрат, на якому показано навчання моделі з такою швидкістю, за якої вона швидко збігається.
Натомість якщо швидкість навчання замала, для збіжності моделі може знадобитися надто багато ітерацій. На рисунку 22 крива втрат демонструє, що з кожною ітерацією модель покращується лише незначною мірою.
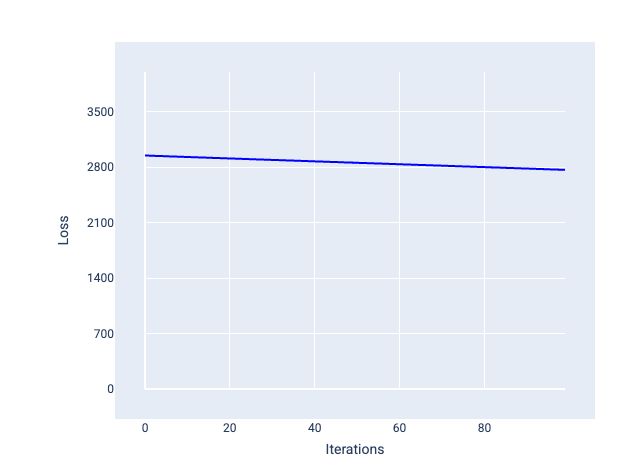
Рисунок 22. Графік втрат, на якому показано модель, що навчалася з невеликою швидкістю.
Якщо швидкість навчання завелика, неможливо досягти збіжності, тому що при кожній ітерації втрати або коливаються, або постійно зростають. На рисунку 23 крива втрат демонструє, що після кожної ітерації втрати моделі зменшуються, а потім збільшуються, а на рисунку 24 втрати збільшуються під час наступних ітерацій.
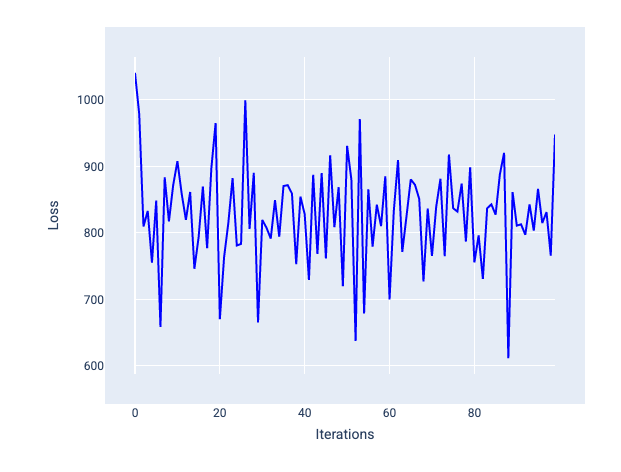
Рисунок 23. Графік втрат, на якому показано модель, що навчалася із завеликою швидкістю: крива втрат нагадує ламану лінію, яка зі збільшенням кількості ітерацій хаотично то підіймається, то падає.
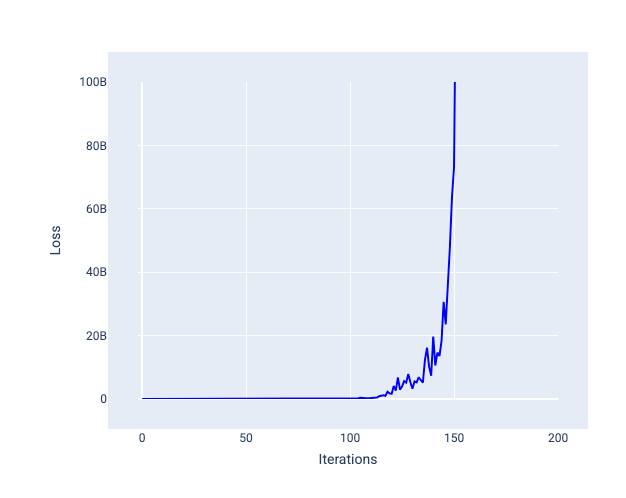
Рисунок 24. Графік втрат, на якому показано модель, що навчалася із завеликою швидкістю: крива втрат різко підіймається при наступних ітераціях.
Вправа. Перевірте свої знання
Розмір пакета
Розмір пакета – це гіперпараметр, що означає кількість прикладів, які обробляє модель, перш ніж оновити значення ваги й упередженості. Ви можете вважати, що модель має обчислювати втрати для кожного прикладу з набору даних, перш ніж оновлювати значення ваги й упередженості. Однак у наборі даних можуть бути сотні тисяч або навіть мільйони прикладів, і тоді використовувати повний пакет недоцільно.
Щоб отримати правильний градієнт в усередненому значенні, не переглядаючи кожен приклад із набору даних перед оновленням значень ваги й упередженості, найчастіше використовуються ці два методи: стохастичний градієнтний спуск і мініпакетний стохастичний градієнтний спуск.
Стохастичний градієнтний спуск (SGD). У цьому методі використовується лише один приклад (розмір пакета дорівнює одиниці) за ітерацію. За умови достатньої кількості ітерацій SGD працює, але генерує дуже багато шуму. "Шум" означає варіації, що з’являються під час навчання й спричиняють збільшення, а не зменшення втрат упродовж ітерації. Термін "стохастичний" означає, що один приклад, який входить у кожен пакет, вибирається випадковим чином.
Зверніть увагу на те, як на наступному зображенні втрати трохи коливаються, коли модель оновлює значення ваги й упередженості за допомогою SGD, що може призвести до появи шуму на графіку втрат.
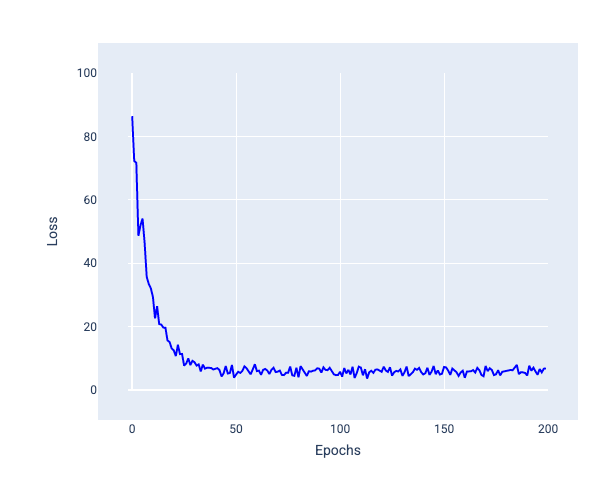
Рисунок 25. Шум на кривій втрат моделі, яка навчалася за допомогою стохастичного градієнтного спуску (SGD).
Зверніть увагу: при використанні стохастичного градієнтного спуску може виникати шум на всій кривій втрат, а не лише поблизу точки збіжності.
Мініпакетний стохастичний градієнтний спуск (мініпакетний SGD). Це компроміс між обробкою повних пакетів і SGD. Для $ N $ точок даних розмір пакета може бути будь-яким числом, більшим ніж 1 і меншим за $ N $. Модель випадковим чином вибирає приклади, що входять у кожен пакет, усереднює їх градієнти, а потім оновлює значення ваги й упередженості один раз за ітерацію.
Визначення кількості прикладів для кожного пакета залежить від набору даних і доступних обчислювальних ресурсів. Загалом невеликі пакети обробляються за допомогою SGD, а великі – градієнтного спуску для всього пакета.
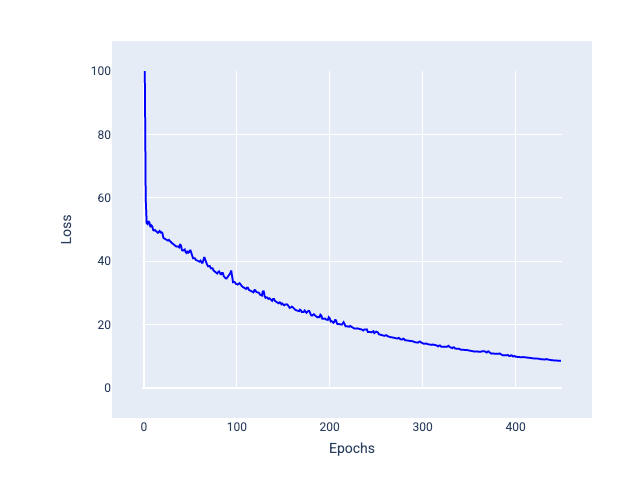
Рисунок 26. Модель, яка навчалася за допомогою мініпакетного стохастичного градієнтного спуску.
Навчаючи модель, ви можете подумати, що шум – це небажана характеристика, яку слід усунути. Однак певна кількість шуму може бути корисною. У наступних модулях ви дізнаєтеся, як шум може допомогти моделі краще узагальнювати й знаходити оптимальні значення ваги та упередженості в нейронній мережі.
Епохи
У контексті тренування моделі епоха означає, що модель обробила кожен приклад із навчального набору один раз. Скажімо, навчальний набір складається з 1000 прикладів, з яких у мініпакет входять 100. Тоді моделі знадобиться 10 ітерацій, щоб завершити одну епоху.
Зазвичай навчання триває багато епох. Це означає, що системі потрібно обробити кожен приклад із навчального набору кілька разів.
Кількість епох – це гіперпараметр, який ви задаєте, перш ніж запустити навчання моделі. Часто важко передбачити, скільки епох знадобиться, щоб модель досягла збіжності, тож доведеться експериментувати. Загалом що більше епох, то краща модель, але через це навчання триватиме довше.
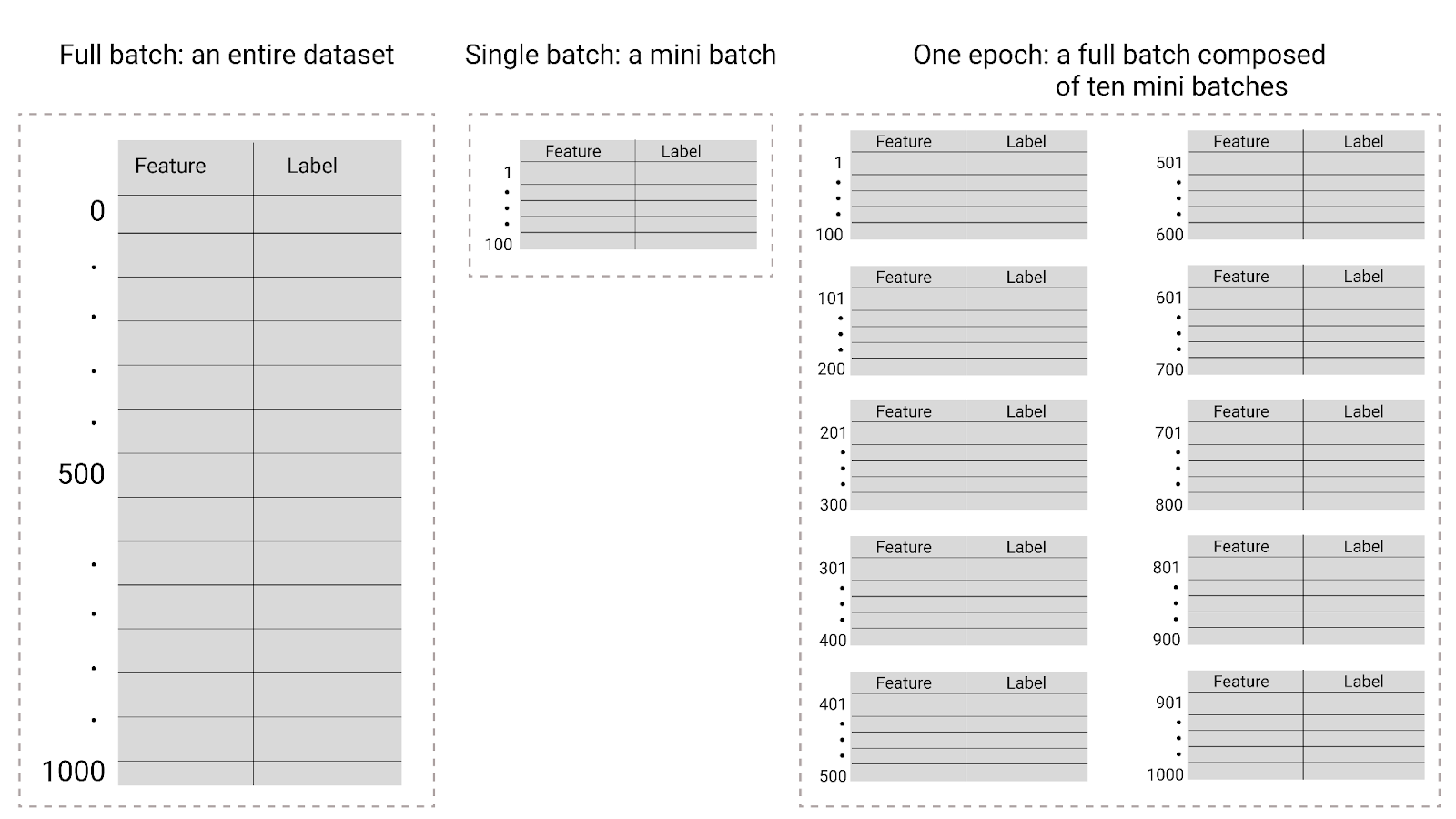
Рисунок 27. Повний пакет проти мініпакета.
У наступній таблиці описано, як розмір пакета й епохи пов’язані з кількістю разів, коли модель оновлює свої параметри.
| Тип пакета | Коли оновлюються значення ваги й упередженості |
|---|---|
| Повний пакет | Після того, як модель переглядає всі приклади з набору даних. Якщо в наборі даних міститься 1000 прикладів і модель навчається впродовж 20 епох, вона оновлює значення ваги й упередженості 20 разів, тобто один раз на кожну епоху. |
| Стохастичний градієнтний спуск | Після того, як модель переглядає один приклад із набору даних. Якщо в наборі даних міститься 1000 прикладів і модель навчається впродовж 20 епох, вона оновлює значення ваги й упередженості 20 000 разів. |
| Мініпакетний стохастичний градієнтний спуск | Після того, як модель переглядає приклади з кожного пакета. Якщо в наборі даних міститься 1000 прикладів, розмір пакета дорівнює 100 й модель навчається впродовж 20 епох, вона оновлює значення ваги й упередженості 200 разів. |